Answers
Answer: 2/3
Step-by-step explanation:
Slope = rise/run
Up 2 and to the right 3
Related Questions
I need help on this ASAP

Answers
Answer:
The question is wrong
Step-by-step explanation:
neither is the value of x given, nor the value of SU line
The perimeter of a square must be greater than 90 inches but less than 108 inches. Find the range of possible side lengths that satisfy these conditions. (Hint: Theperimeter of a square is given by P = 4s, where s represents the length of a side)Express your answer in interval notation. Use decimal form for numerical values.
Answers
The perimeter of a square can be found using the following formula:
\(P=4s\)Where "s" is the length of any side of the square.
Then, an expression that represents the perimeter of a square can be:
\(4s\)You know that it must be greater that 90 inches be less than 108 inches. Then, using this information, you can set up that:
\(90<4s<108\)Now, in order to find the range of possible side lengths asked in the exercise, you need to divide 90 and 108 by 4, as you can see below:
\(\begin{gathered} \frac{90}{4}Therefore, the answer expressed in Interval notation, is:\((22.5,27)\)Which function is represented by the graph? f(x) = â’|x â’ 3| 4 f(x) = â’|x 3| 4 f(x) = â’|x â’ 4| 3 f(x) = â’|x 4| 3.
Answers
Functions are used to represent graphs, and vice versa.
The function represented by the graph is \(f(x) =- |x + 4| + 3\)
The graph (see attachment) is an absolute value graph.
An absolute value graph is represented as:
\(f(x) =a |x - h| + k\)
Where
\(Vertex = (h,k)\)
The vertex is the minimum or the maximum point on the graph.
So, we have:
\(Vertex = (-4,3)\)
The function becomes
\(f(x) =a |x + 4| + 3\)
The function also passes through the point (-1,0).
So, we have:
\(0 =a |-1 + 4| + 3\)
\(0 =a |3| + 3\)
Remove the absolute bracket
\(0 =3a + 3\)
Subtract 3 from both sides
\(3a =- 3\)
Divide both sides by 3
\(a =- 1\)
Substitute -1 for (a) in \(f(x) =a |x + 4| + 3\)
\(f(x) =- |x + 4| + 3\)
Hence, the function represented by the graph is \(f(x) =- |x + 4| + 3\)
Read more about absolute value graphs at:
https://brainly.com/question/3381225

are they parallel perpendicular or neither.

Answers
Answer:
parallel
Step-by-step explanation:
What is the 3rd terms of the sequence:
f(1)=-3, f(n)= f(n-1)+5
Answers
Answer:
f(3) = 7
Step-by-step explanation:
Using the recursive formula and f(1) = - 3 , then
f(2) = f(1) + 5 = - 3 + 5 = 2
f(3) = f(2) + 5 = 2 + 5 = 7
If the observations have weights of 2, 3 and 1 respectively, solve these equations for the most probable values of A and B using weighted least squares method. Solve the problem using both algebraic approach and matrices and compare your results.
A+2B=10.50+V1
2A-3B=5.55+V2
2A-B=-10.50+V3
Answers
The results obtained using the algebraic approach and the matrix approach should be the same. Both methods are mathematically equivalent and provide the most probable values of A and B that minimize the sum of squared weighted residuals.
To solve the system of equations using the weighted least squares method, we need to minimize the sum of the squared weighted residuals. Let's solve the problem using both the algebraic approach and matrices.
Algebraic Approach:
We have the following equations:
A + 2B = 10.50 + V1 ... (1)
2A - 3B = 5.55 + V2 ... (2)
2A - B = -10.50 + V3 ... (3)
To minimize the sum of squared weighted residuals, we square each equation and multiply them by their respective weights:
\(2^2 * (A + 2B - 10.50 - V1)^2\)
\(3^2 * (2A - 3B - 5.55 - V2)^2\\1^2 * (2A - B + 10.50 + V3)^2\)
Expanding and simplifying these equations, we get:
\(4(A^2 + 4B^2 + 10.50^2 + V1^2 + 2AB - 21A - 42B + 21V1)\\9(4A^2 + 9B^2 + 5.55^2 + V2^2 + 12AB - 33A + 16.65B - 11.1V2)\\(A^2 + B^2 + 10.50^2 + V3^2 + 2AB + 21A - 21B + 21V3)\\\)
Now, let's sum up these equations:
\(4(A^2 + 4B^2 + 10.50^2 + V1^2 + 2AB - 21A - 42B + 21V1) +\\9(4A^2 + 9B^2 + 5.55^2 + V2^2 + 12AB - 33A + 16.65B - 11.1V2) +\\(A^2 + B^2 + 10.50^2 + V3^2 + 2AB + 21A - 21B + 21V3)\int\limits^a_b {x} \, dx\)
Simplifying further, we obtain:
\(14A^2 + 31B^2 + 1113 + 14V1^2 + 33V2^2 + 14V3^2 + 14AB - 231A - 246B + 21V1 - 11.1V2 + 21V3 = 0\)
Now, we have a single equation with two unknowns, A and B. We can use various methods, such as substitution or elimination, to solve for A and B. Once the values of A and B are determined, we can substitute them back into the original equations to find the most probable values of A and B.
Matrix Approach:
We can rewrite the system of equations in matrix form as follows:
| 1 2 | | A | | 10.50 + V1 |
| 2 -3 | | B | = | 5.55 + V2 |
| 2 -1 | | -10.50 + V3 |
Let's denote the coefficient matrix as X, the variable matrix as Y, and the constant matrix as Z. Then the equation becomes:
X * Y = Z
To solve for Y, we can multiply both sides of the equation by the inverse of X:
X^(-1) * (X * Y) = X^(-1) * Z
Y = X^(-1) * Z
By calculating the inverse of X and multiplying it by Z, we can find the values of A and B.
Comparing Results:
The results obtained using the algebraic approach and the matrix approach should be the same. Both methods are mathematically equivalent and provide the most probable values of A and B that minimize the sum of squared weighted residuals.
For more such questions on matrix visit:
https://brainly.com/question/1279486
#SPJ8
Convert the rectangular equation to polar form. X2 y2 = 64
Answers
The polar form of the equation represents all the points with a distance of 8 from the origin, which is a circumference with a radius of 8, centered on the origin.
What is the polar form of the equation?The polar form is represented with the aid of polar coordinates of real and imaginary numbers in the coordinate system.
The horizontal and the vertical axis of the polar form denote the real axis and the imaginary axis, respectively.
The given equation to polar form is;
\(\rm x^2+y^2=64\)
Using the formulae that link Cartesian to Polar coordinates.
x = rcosθ and y = rsinθ
Substitute these values into the equation.
\(\rm x^2+y^2=64\\\\(rcos\theta)^2+(rsin\theta)^2=64\\\\r^2cos^2\theta +r^2sin^2\theta =64\\\\r^2(cos\theta^2+sin\theta^2)=64\\\\Where ; \ sin^2\theta + cos^2\theta=1\\\\r^2(1)=64\\\\ r^2=8^2\\\\r=8\)
Hence, the polar form of the equation represents all the points with a distance of 8 from the origin, which is a circumference with a radius of 8, centered on the origin.
Learn more about polar form here;
https://brainly.com/question/13732976
#SPJ4
Hey guys! I really need help on this question.. Im stuck on it lol.
If you can help then tysm :)

Answers
Answer:
The average size of a seventh - grade class is larger and varies more than that of kindergarten class.
PLEASE MARK ME BRAINLIESTif a regulation basketball is randomly selected, what is the probability that it will weigh between 20.5 and 23.5 ounces?
Answers
Therefore, the probability that basketball will weigh between 20.5 and 23.5 is 0.866
What is probability ?Probability is the concept that describes the likelihood of an event occurring. In real life, we frequently have to make predictions about how things will turn out. We may be aware of the result of an occurrence or not. When this is the case, we refer to the likelihood that the event will occur or not.
Here,
X υ N (22,1)
Probability that basketball will weigh between 20.5 and 23.5
is:
=> P(20.5 < x < 23.5)= P[ 20.5-22/1 < z < 23.5-22/ 1 ]
=> P(20.5 < x < 23.5) = P(-1.5 < z < 1.5)
=> P(20.5 < x < 23.5) = 0.866
Therefore, the probability that basketball will weigh between 20.5 and 23.5 is 0.866
To know more about probability , visit
https://brainly.com/question/11234923
#SPJ4
The sum of two numbers is 32 One number is 8 more than the other. Identify the system of equations representing this problem
Answers
Answer:
x + y = 32
x = y + 8
Step-by-step explanation:
Sum of two numbers is 32:
x + y = 32
One number is 8 more than the other:
x = y + 8
Point: (-4,-6), slope: 7/3
Draw a graph
Answers
Here is the graph of the point (-4, -6) with a slope of 7/3.
To create the graph, start at the point (-4,-6) and plot it on the coordinate axis. From there, use the slope of 7/3 to find another point on the same line. To do this, you can move 7 units up and 3 units to the right from the point (-4,-6) to get to the point ( -1, -1). Plot this point on the graph as well. Finally, draw a straight line passing through both points to get the line representing the equation of the given point and slope.
what is the slope of the line 3y-x=-6
Answers
A candy factory makes 292,827 candies each day. About how many candies will it make in two weeks?
Choose the best estimate.
4,180,0004 comma 180 comma 000
4,200,0004 comma 200 comma 000
4,102,0004 comma 102 comma 000
4,060,0004 comma 060 comma 000
Answers
Answer:
4,102,0004 comma 102 comma 000
Step-by-step explanation:
If it makes 292,827 candies in a day, to find the approximate value of candies produced in 2 weeks, you have to multiply 292,827 by 14, being 14 days in 2 weeks. But since this is just rounding, the easiest option is just to find the actual answer and see which one is closest.
this is URGENT BESTIES

Answers
Answer:
675 \(ft^2\)
Step-by-step explanation:
The radius is 15, so replace r in the formula with 15
\(A=\pi 15^2\)
A = 225 pi
A = 675
(using 3 for pi, since they specified)
Answer: 675
Step-by-step explanation:
In parallelogram PQRS, QP is entended to pointT and ST is drawn
Answers
Answer
Angle PST = 80°
Explanation
Opposite angles of a parallelogram are equal.
Angle R = 130° = Angle QPS
The sum of angles on a straight line is 180°.
Angle QPS + Angle SPT = 180°
130° + Angle SPT = 180°
Angle SPT = 180° - 130° = 50°
Then, we were told that ST = SP, so, the the base angles of triangle PST are equal.
Angle SPT = Angle STP = 50°
Sum of angles in a triangle = 180°
Angle SPT + Angle STP + Angle PST = 180°
50° + 50° + Angle PST = 180°
100° + Angle PST = 180°
Angle PST = 180° - 100°
Angle PST = 80°
Hope this Helps!!!
man I hate USA test prep pls help I have to do this s8it every Friday

Answers
Question 7=C
I am 100% sure this is correct
What do you mean by 184x9302
Answers
Answer:
1711568
Step-by-step explanation:
184*9302 = 1711568
Use a calculator to check your work
emma is moving to a large city and is investigating typical monthly rental prices of available one-bedroom apartments. she obtained a random sample of rental prices for 50 one-bedroom apartments taken from a web site where people voluntarily list available apartments. (a) describe the population for which it is appropriate for emma to generalize the results from her sample.
Answers
The population for which it is appropriate for Emma to generalize the results from her sample is the population of one-bedroom apartment rental prices in the large city where Emma is moving.
This population includes all the prices of one-bedroom apartments that are available for rent in that city, not just the ones that are listed on the website where Emma obtained her sample. Emma is most likely to be utilizing the information from her sample to make inferences about the population as a whole, such as the typical monthly rental prices, the range of prices, and the distribution of prices.
Learn more about statistics and sampling in real estate/housing here: https://brainly.com/question/18296681
#SPJ4
A certain type of insect has a 0.2 chance of dyingonanyonedayandthisprobability remains relatively constant for a few days.
a. Whatistheprobabilitythataninsectof this type survives its first day?
b. Whatistheprobabilitythataninsectof this type survives its first three days?
c. Whatistheprobabilitythataninsectof this type dies on its fourth day?
d. How many days do you expect an insect of this type to survive?
e. If 200 insects of this type are being studied in a laboratory, how many do you expect to be alive after the third day?
Answers
The answer to each question are:
a). probability of an insect of this type surviving its first day is 0.8
b). probability of an insect of this type surviving it's first three days is 0.512.
c). probability of an insect of this type dying on its fourth day is 0.2.
d). If 200 insects of this type are being studied in a laboratory, 102 to be alive after the third day.
What is the probability?
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are.
a). The probability that an insect of this type survives its first day is 1 - 0.2 = 0.8.
b). The probability that an insect of this type survives it's first three days is 0.8 * 0.8 * 0.8 = 0.512.
c). The probability that an insect of this type dies on its fourth day is 0.2.
d). The expected number of days that an insect of this type would survive is not determinable with the information given.
e). If 200 insects of this type are being studied in a laboratory, you would expect approximately 200 * 0.512 = 102.24 to be alive after the third day. Round down to 102 insects.
Hence, The answer to each question is:
a). probability of an insect of this type surviving its first day is 0.8
b). probability of an insect of this type surviving it's first three days is 0.512.
c). probability of an insect of this type dying on its fourth day is 0.2.
d). If 200 insects of this type are being studied in a laboratory, 102 to be alive after the third day.
To learn more about probability visit,
https://brainly.com/question/25839839
#SPJ1
Which diagram represents a fraction equivalent to 75%?
A bar diagram with 14 shaded squares and 6 unshaded squares.
A bar diagram with 8 shaded squares and 2 unshaded squares.
A bar diagram with 15 shaded squares and 5 unshaded squares.
A bar diagram with 7 shaded squares and 3 unshaded squares.
Mark this and return
Answers
Answer: Third figure with 15 boxes being filled out of 20 total boxes.
Step-by-step explanation:
Given:
A fraction equivalent to 75% from the given figures.
Now, let us check each option.
Option 1: There are 20 boxes out of which 14 are filled. So, percentage of filled boxes is given as:
Option 2:
There are 10 boxes out of which 8 are filled. So, percentage of filled boxes is given as:
Option 3:
There are 20 boxes out of which 15 are filled. So, percentage of filled boxes is given as:
Option 4: There are 10 boxes out of which 7 are filled. So, percentage of filled boxes is given as:
Among all the options, only the third option has answer as 75%. So, third option is the correct answer.
Answer:
C
Step-by-step explanation:
Verify the divergence theorem for the given region W, boundary ∂W oriented outward, and vector field F. W = [0, 1] ✕ [0, 1] ✕ [0, 1] F = 2xi + 3yj + 2zk
Answers
Verify the divergence theorem for the given region W, boundary ∂W oriented outward, and vector field F. W = [0, 1] ✕ [0, 1] ✕ [0, 1] F = 2xi + 3yj + 2zk
The divergence theorem is correct and verified by using the formula S = ∫∫(F . n) dS = ∫∫∫(∇ . F) dV where,∇ . F is the divergence of the given vector field.
Divergence theorem: The divergence theorem states that the flux of a vector field through a closed surface is equal to the volume integral of the divergence over the region enclosed by the surface. Here, it is given to verify the divergence theorem for the given region W, boundary ∂W oriented outward, and vector field F, which is given as,W = [0, 1] x [0, 1] x [0, 1]F = 2xi + 3yj + 2zkHere, we need to find the flux of the given vector field through the boundary of the given region W using the divergence theorem. We know that the flux of a vector field F through the closed surface S is given by, Flux of F through S = ∫∫(F . n) dS Where n is the outward pointing unit normal to the surface S.In the divergence theorem, the flux of F through the closed surface S is given by, Flux of F through S = ∫∫(F . n) dS = ∫∫∫(∇ . F) dV where,∇ . F is the divergence of the given vector field F and V is the volume enclosed by the surface S.Now, let us find the divergence of the given vector field F, which is given by,F = 2xi + 3yj + 2zk
∇ . F = ∂(2x)/∂x + ∂(3y)/∂y + ∂(2z)/∂z= 2 + 3 + 2= 7
Therefore, the divergence of the given vector field F is 7.
Now, let us find the volume of the given region W using the triple integral, Volume of W = ∫∫∫dV= ∫[0,1]∫[0,1]∫[0,1]dxdydz= ∫[0,1]∫[0,1]1dx dy= ∫[0,1]dx= 1
Therefore, the volume of the given region W is 1. Now, using the divergence theorem, we can find the flux of the given vector field F through the boundary of the given region W, which is given by, Flux of F through the boundary of W = ∫∫(F . n) dS = ∫∫∫(∇ . F) dV= ∫∫∫ 7 dV= 7 * Volume of W= 7 * 1= 7. Therefore, the flux of the given vector field F through the boundary of the given region W is 7.
Hence verified.
Learn more about the Divergence theorem: https://brainly.com/question/17177764
#SPJ11
In the year 2004, the Castle family
purchased a home in Mesquite for $215,000,
Each year since 2004, the value of the home
has increased on average by about 2.75%
over the value from the previous year.
Which function models the value of the
Castle's home x years since 2004?
Answers
The function that models the value of the Castle family's home x years since 2004 is V(x) = $215,000 * (1 + 0.0275)^x.
To model the value of the Castle family's home x years since 2004, we need to consider the annual increase in value. Since the value of the home increases by an average of 2.75% each year, we can express this as a decimal by dividing it by 100, resulting in 0.0275.
Using the initial value of $215,000 in 2004, we can represent the value of the home x years later as V(x). To account for the annual increase, we multiply the initial value by (1 + 0.0275)^x, where x represents the number of years since 2004.
Therefore, the function that models the value of the Castle family's home x years since 2004 is V(x) = $215,000 * (1 + 0.0275)^x, where V(x) represents the value of the home in dollars after x years since 2004.
Learn more about function here:
https://brainly.com/question/28278690
#SPJ11
given a list of a finishing times at a marathon, which function should you use to rank each runner's place based on these finishing times?
Answers
Answer:
Below
Step-by-step explanation:
Rank in order of SHORTEST time to LONGEST time ....
shorter times mean the runner was faster to the finish line.
For the following question, show representation, your initial equations, your algebra work, symbolic answer, and units check.
A dog is sitting at an initial position of D1= (50 m North, 10 m East) from her home. She moves in a straight line until she is at a final position of D2 = ( 5 m North, 35 m East) from her home. It takes her 15 seconds to move from the initial position to the final position; find the magnitude of her average velocity vector.
Answers
The magnitude of the average velocity vector is approximately 3.651 m/s.
To find the magnitude of the average velocity vector, we need to calculate the displacement and divide it by the time taken.
Representation:
Initial position: D1 = (50 m North, 10 m East)
Final position: D2 = (5 m North, 35 m East)
Time taken: t = 15 seconds
Equations:
Displacement vector (ΔD) = D2 - D1
Average velocity vector (\(V_{avg}\)) = ΔD / t
Algebra work:
ΔD = D2 - D1
= (5 m North, 35 m East) - (50 m North, 10 m East)
= (-45 m North, 25 m East)
|ΔD| = √((-45)^2 + 25^2) [Magnitude of the displacement vector]
\(V_{avg}\) = ΔD / t
= (-45 m North, 25 m East) / 15 s
= (-3 m/s North, 5/3 m/s East)
|\(V_{avg}\)| = √((-3)^2 + (5/3)^2) [Magnitude of the average velocity vector]
Symbolic answer:
The magnitude of the average velocity vector is approximately 3.651 m/s.
Units check:
The units for displacement are in meters (m) and time in seconds (s). The average velocity is therefore in meters per second (m/s), which confirms the units are consistent with the calculation.
Therefore, the magnitude of the average velocity vector is approximately 3.651 m/s.
Learn more about vector here: https://brainly.com/question/24256726
#SPJ11
PLEASE ANSWER THIS QUESTION 50 POINTS RIGHT ANSWERS ONLY
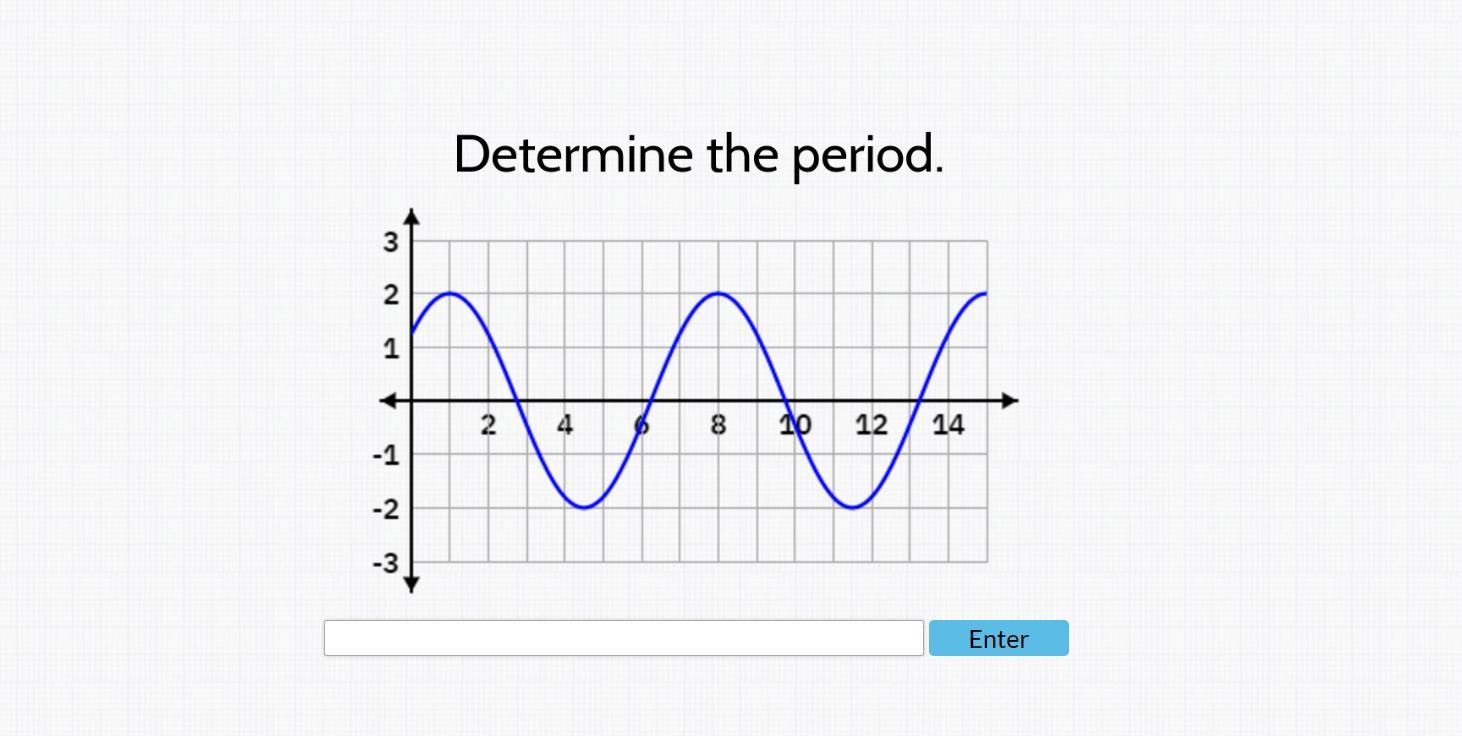
Answers
Answer:
The period of this graph is 7.
1421MiliLiter into liter
Answers
Answer:
1.421 liters
Step-by-step explanation:
Plz mark B R A I N L I E S T
Calculate the perimeter of this shape???

Answers
Answer:
60 cmStep-by-step explanation:
moving the two segments as in the figure I put, the perimeter doesn't change.
P = 2(length + breadth)
2 x (12 + 18) = 60 cm

BP has a bond outstanding with 15 years to maturity, a $1,000 par value, a coupon rate of 6.9%, with coupons paid semiannually, and a price of 98.17 (percent of par) 18 | Attempt 1/10 for 10 pts. Part 1 What is the cost of debt?
Answers
There is an outstanding bond from BP with a 15-year maturity, a $1,000 par value, a 6.9% coupon rate that is paid semi-annually, and a price of 98.17. As a result, the annual cost of debt for this bond is roughly 8.5 percent.
To calculate the cost of debt, we need to determine the yield to maturity (YTM) of the bond. The YTM is the rate of return an investor would earn by purchasing the bond and holding it until maturity. We can use the bond pricing formula to calculate the YTM.
The bond pricing formula is as follows:
\(\text{Bond Price} = \frac{{C \times (1 - (1 + r)^{-n})}}{{r}} + \frac{{M}}{{(1 + r)^n}}\)
Where:
C = Coupon payment
r = Yield to maturity (YTM)
n = Number of periods
M = Par value
Given information:
Coupon payment (C) = \(\$1,000 \times \frac{6.1\%}{2} = \$30.50\)
Par value (M) = $1,000
Bond price = $1,000 × 83.57% = $835.70
We know the bond has 15 years to maturity, and coupons are paid semiannually. So, the number of periods (n) is 15 years × 2 = 30.
Using the bond pricing formula, we can rearrange it to solve for the YTM:
\(Bond Price = \frac{{C \times (1 - (1 + r)^{-n})}}{{r}} + \frac{{M}}{{(1 + r)^n}}\)
Substituting the given values:
\($835.70 = \left(\frac{{\$30.50 \times (1 - (1 + r)^{-30})}}{{r}}\right) + \left(\frac{{\$1,000}}{{(1 + r)^{30}}}\right)\)
To find the YTM, we need to solve this equation either algebraically or using numerical methods like trial and error or using financial calculators/spreadsheets.
By using a financial calculator or spreadsheet, we find that the YTM is approximately 8.5%. Therefore, the cost of debt for this bond is approximately 8.5% per year.
To know more about the yield to maturity refer here :
https://brainly.com/question/26376004#
#SPJ11
Complete question :
Problem 17 Intro BP has a bond outstanding with 15 years to maturity, a $1,000 par value, a coupon rate of 6.1%, with coupons paid semiannually, and a price of 83.57 (percent of par). | Attempt 1/10 for 10 pts. Part 1 What is the cost of debt? B+ decimals Submit
If the range of a distribution were 120 and the data were reported as whole numbers, what would i (the width of the class interval) be if one chose to group the distribution into approximately 15 class intervals
Answers
To determine the width of the class interval (i) when grouping a distribution into approximately 15 class intervals.
Given that the range of the distribution is 120 and the data are reported as whole numbers, we can use the following formula:
i = range / number of class intervals
In this case, we want to have approximately 15 class intervals, so the number of class intervals would be 15.
i = 120 / 15 = 8
Therefore, if you choose to group the distribution into approximately 15 class intervals and the range of the distribution is 120, the width of each class interval (i) would be 8.
Learn more about range here:
https://brainly.com/question/29204101
#SPJ11
two functions are given below: f(x) and h(x). state the axis of symmetry for each function and explain how to find it
HELP ME PLEASE

Answers
The axis of symmetry for function
f(x) is x = 8 and for h(x) is x = 3.
We know that the quadratic equation in vertex form is, y = a (x - m)² + n
where (m, n) is the vertex of the parabola.
And, the axis of symmetry is x = m.
Consider function f(x)
f(x) = -4(x - 8)² + 3
This function represents a quadratic equation in vertex form with vertex (8, 3)
So, the axis of symmetry for function f(x) would be x = 8
We know that the axis of symmetry is the vertical line that goes through the vertex of a parabola so the left and right sides of the parabola are symmetrical.
Consider the function h(x)
We can observe that the vertex of parabola is (3, 2)
So, the axis of symmetry would be x = 3.
Therefore, the axis of symmetry for function
f(x) is x = 8 and for h(x) is x = 3.
Learn more about the axis of symmetry here:
https://brainly.com/question/22495480
#SPJ1
