What is the solution to the system graph?
Answers
The ordered pair that is a solution to both equations is the solution of such a system graph.
What is a system graph?We graph both equations using the same coordinate system to solve a system of linear equations graphically. The system's solution will be found where the two lines intersect.A system of linear equations consists of two or more equations, such as y=0.5x+2 and y=x-2. The ordered pair that is a solution to both equations is the solution to such a system. Inorder to solve a system of linear equations graphically, we graph both equations in the same coordinate system.The ordered pair that is a solution to both equations is the solution to such a system. The system's solution will be found at the intersection of the two lines.To learn more about system of graph refer to :
https://brainly.com/question/14323743
#SPJ1
Related Questions
Erica has two pieces of thread, one 14 feet long and the other 4 feet long. For a sewing project, she needs to cut them up to produce many pieces of thread that are all of the same length, with no thread left over. What is the greatest length, in feet, that she can make them?
Answers
Answer:
Step-by-step explanation:So to find the greatest common divisor, we need to factor these numbers.
4 = 2*214=2*7The same ones that matches each other is 2
so, the thread must be cut by 2 feet each to match the requirements that were given.
Select the correct answer.
The Cohen family started their wheat farm in 1995. The equation models the number of bushels of wheat they produced each year, where tis
the number of years since 1995.
C(t)= 7,000+500 In(t + 1)
The Mason family also started their wheat farm in 1995. The graph models the number of bushels of wheat they produced each year, where t
is the number of years since 1995.
M(t)

Answers
A graph is a way to represent a lot of data in such a visual format that it is easy for the user to understand the complete information in one go. The correct statement is D.
What is a graph?A graph is a way to represent a lot of data in such a visual format that it is easy for the user to understand the complete information in one go. Usually, the line of the graph is a function that follows the graph.
If we draw the graph of the Cohen family, then the graph will look as shown below. Therefore, if we observe the graph of the Cohen family and the graph of the Mason family. Then we will observe that the wheat production of both farms will approach a stable amount as the years pass.
Hence, the correct statement is D.
Learn more about Graph:
https://brainly.com/question/21608293
#SPJ1

HELP! Use a rational equation to solve: In the
aquarium, 90% of the fish are blue. The rest of
the fish are red. The blue fish number 10 more
than twice the number of red fish.
Answers
There are approximately 1.43 red fish and 2.86 blue fish in the aquarium.
what is algebra?
Algebra is a branch of mathematics that deals with mathematical operations and symbols used to represent numbers and quantities in equations and formulas.
Let's start by defining some variables to represent the unknown quantities in the problem. Let's call the number of red fish "r" and the number of blue fish "b".
We know that 90% of the fish are blue, which means that the remaining 10% are red. So we can write:
b = 0.9(b + r) (since blue fish = 90% of total fish)
r = 0.1(b + r) (since red fish = 10% of total fish)
We also know that the number of blue fish is 10 more than twice the number of red fish:
b = 2r + 10
Now we can use the first equation to solve for one of the variables in terms of the other. Let's solve for "r":
r = 0.1(b + r)
10r = b + r (multiply both sides by 10)
9r = b (subtract "r" from both sides)
Now we can substitute this expression for "b" in the second equation:
b = 2r + 10
9r = 2r + 10
7r = 10
r = 10/7
So there are approximately 1.43 red fish in the aquarium. To find the number of blue fish, we can substitute this value for "r" in the equation we found earlier:
b = 2r + 10
b = 2(10/7) + 10
b = 20/7
So there are approximately 2.86 blue fish in the aquarium.
Therefore, there are approximately 1.43 red fish and 2.86 blue fish in the aquarium.
To learn more about algebra from the given link:
https://brainly.com/question/24875240
#SPJ1
write 300/1,100 as a percent
Answers
Answer:
27.3%
Step-by-step explanation:
300/1100 = 0.2727
to get percentage we multiply ^^ by 100
so = 27.27% or rounded to nearest tenth = 27.3
Mariza é costureira e, para determinar o comprimento de elástico, em cm, que utiliza na confecção de determinado modelo de calça, ela recorre à expressão x2+2y . Nessa expressão, x e y são medidas que variam de acordo com o tamanho da calça a ser produzida. Para o tamanho P dessa calça, ela utiliza x=40 cm e y=15 cm
Answers
40(2) + 15(2) = 80 + 30 = 110 :)
suppose that shoe sizes of american women have a bell-shaped distribution with a mean of 8.04 and a standard deviation of 1.53 . using the empirical rule, what percentage of american women have shoe sizes that are less than 11.1 ?
Answers
The percentage of American women that have shoe sizes that are at least 11.1 is; 0.0015
Empirical Rule
We are given;
Mean; x' = 8.04
Standard deviation; σ = 1.53
Using the empirical rule, we can have the data either 1, 2, or 3 standard deviations from the mean.
Thus;
At 1 standard deviation from the mean, we have;
8.04 ± 1(1.53)
⇒ (6.52, 8.56)
At 2 standard deviations from the mean, we have;
8.04 ± 2(1.53)
⇒ (5, 11.08)
At 3 standard deviations from the mean, we have;
8.04 ± 3(1.52)
⇒ (3.48, 12.6)
We can see that the one with at least 12,6 is 3 standard deviations from the mean which from the empirical rule is 99.7%
Thus;
percentage of American women have shoe sizes that are at least 12.6 = 100% - 99.7% - 0.15%
P(x ≥ 12.6) = 0.15% = 0.0015
To know more about empirical value:
https://brainly.com/question/18529739
#SPJ4
I need help with this Graph!
Graph a right triangle with the two points forming the hypotenuse. Using the sides, find the distance between the two points, to the nearest tenth (if necessary). (-6,3) and (3, -9)
find leg number 1 and leg number 2 and the distance

Answers
Answer:
Step-by-step explanation:

The distance between two points (-6, 3) and (3, -9) is 10.81 units.
We have a graph a right triangle with the two points A(-6,3) and B(3, -9) forming the hypotenuse.
We have find the distance between the two points using only the sides of the right triangle.
What is the formula to find the distance between the two points on Cartesian plane ?The distance between two points -
\(d = \sqrt {\left( {x_1 - x_2 } \right)^2 + \left( {y_1 - y_2 } \right)^2 }\)
According to the question, we have -
Coordinates of Point A = (- 6, 3)
Coordinates of Point C = (3, -9)
Now -
Coordinates of Point B will be (- 6, -9) [formed by the intersection of sides].
Distance AB -\(AB = \sqrt {\left( {-6 - (-6) } \right)^2 + \left( {3 - (-9 } \right)^2 }\) = 6 units
Distance BC -\(BC = \sqrt {\left( {-6 - 3 } \right)^2 + \left( {-9 - (-9 } \right)^2 }\) = 9 units
Using the Pythagoras theorem -
\((AC)^{2} =(AB)^{2} +(BC)^{2}\)
\((AC)^{2} =\) 36 + 81
AC = \(\sqrt{117}\) = 10.81
Hence, the distance between two points (-6, 3) and (3, -9) is 10.81 units.
To solve more questions on Distance formula, visit the link below -
brainly.com/question/12662141
#SPJ6

What is the answer for
√x+5 +2=√x-7
Answers
Solution: x∈Ф
No solution
Step-by-step explanation:
\(\sqrt{x} +5+2=\sqrt{x} -7\)
\(5+2=-7\)
\(7=-7\)
\(1=-1\)
x∈Ф
determine whether the series is convergent or divergent. 1 1/(2 root3(2)) 1/(3 root3(3)) 1/(4 root3(4)) 1/(5 root3(5)) ...
Answers
the series 1/(n∛(n)) is divergent.
To determine the convergence or divergence of the series, let's examine the terms of the series and apply the comparison test.
The series in question is:
1/(n∛(n))
We can compare it to the harmonic series, which is known to be divergent:
1/n
Let's compare the terms of the given series to the terms of the harmonic series:
1/(n∛(n)) < 1/n
Since 1/n is a divergent series, and the terms of the given series are smaller than the corresponding terms of the harmonic series, we can conclude that the given series is also divergent.
To know more about series visit:
brainly.com/question/11346378
#SPJ11
The difference of a number and eight is the same as 38 less the number find the number
Answers
Answer:
Number = 23Step-by-step explanation:
Let the number be x.\(x - 8 = 38 - x \\ x + x = 38 + 8 \\ 2x = 46 \\ x = 46 \div 2 \\ x = 23\)
The number is 23 if the difference between a number and eight is the same as 38 less the number.
What is a linear equation?It is defined as the relation between two variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
We have:
The difference between a number and eight is the same as 38 less the number.
Let x be the number
x - 8 = 38 - x
2x = 38 + 8
2x = 46
x = 46/2 = 23
Thus, the number is 23 if the difference between a number and eight is the same as 38 less the number.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ2
What is the value of x in the equation
ox5
6x - 5
2
=
2x + 6?
Answers
a plane traveled miles with the wind in hours and miles against the wind in the same amount of time. find the speed of the plane in still air and the speed of the wind.
Answers
Let's represent the speed of the plane in still air as "p" and the speed of the wind as "w".
When the plane is traveling with the wind, its speed is (p + w) and against the wind, its speed is (p - w).
Given that it travels d1 miles with the wind in t hours and d2 miles against the wind in the same time, we can form the following equations:
d1 = t(p + w)
d2 = t(p - w)
Now, we need to solve for "p" and "w". Divide the first equation by t, and the second equation by t as well:
d1/t = p + w
d2/t = p - w
Add the two equations together to eliminate "w":
(d1/t) + (d2/t) = 2p
Solve for "p":
p = (d1 + d2) / (2t)
Now, substitute the value of "p" in either equation to solve for "w":
w = (d1/t) - p
Once you have the specific values for d1, d2, and t, plug them into the equations to find the speed of the plane in still air (p) and the speed of the wind (w).
learn more about speed here:brainly.com/question/28224010
#SPJ11
The area of a square is shown below. Find the side length of the squareand explain how you found your answer.A = 25 in.2
Answers
The side length of the square = 5 in
Explanations:If the side length of a square is represented as L
The area of the square is given by the formula:
Area, A = L²
Since the Area is given in the question as:
A = 25 in²
Substitute the value of A into the formula A = L²
25 = L²
Square root both sides:
\(\begin{gathered} \sqrt{25}=\sqrt{L^2} \\ 5\text{ = L} \\ L\text{ = 5 in} \end{gathered}\)The side length of the square = 5 in
choosing the pivot row by requiring that the ratio associated with that row be the smallest non-negative number ensures that the iteration will not take us from a feasible point to a non-feasible point.
Answers
Answer:
This statement is true.
In the simplex method, choosing the pivot row involves selecting a row with a negative value in the right-hand column and dividing the elements in the last column by the corresponding elements in the selected row to obtain the ratios. The row with the smallest non-negative ratio is then chosen as the pivot row.
By choosing the pivot row in this way, we ensure that the new solution will still be feasible, meaning that all the constraints will still be satisfied. This is because choosing the smallest non-negative ratio ensures that the new solution will not violate any of the non-negativity constraints.
Therefore, requiring that the ratio associated with the pivot row be the smallest non-negative number is an important step in the simplex method to ensure that the iteration will not take us from a feasible point to a non-feasible point.
Step-by-step explanation:
This statement is true when using the simplex method to solve a linear programming problem.
In the simplex method, we start with a feasible solution and iteratively improve it until we reach an optimal solution. At each iteration, we choose a pivot row and a pivot column to pivot around. The pivot row is chosen based on the ratio of the right-hand side value to the coefficient of the entering variable in that row. This ratio is called the pivot ratio.
Choosing the pivot row with the smallest non-negative pivot ratio ensures that we pivot to a new feasible solution. This is because the pivot row represents a constraint in the linear programming problem, and the pivot ratio represents how much we can increase the value of the entering variable while still satisfying that constraint. If the pivot ratio is negative, it means that increasing the entering variable would violate the corresponding constraint, and so we cannot pivot in that direction.
Therefore, by choosing the pivot row with the smallest non-negative pivot ratio, we ensure that we pivot in a direction that preserves feasibility and does not take us to a non-feasible point.
Visit to know more about Simplex method:-
brainly.com/question/30387091
#SPJ11
from a class of 20 students we need to select 3 for a committee, one to be president, another to be vice-president and the third to be secretary. in how many ways can this be done?
Answers
So there are 6,840 possibilities to choose a committee of three students, one as president, one as vice president, and one as secretary.
As per the question given,
We need to select 3 students from a class of 20, where order matters.
The number of ways to select the first student for the committee is 20, since we can choose any of the 20 students.
After selecting the first student, there are 19 students remaining to choose from for the second position (the vice-president). Once the vice-president is selected, there are 18 students remaining to choose from for the third position (the secretary).
Therefore, the total number of ways to select the committee is:
20 * 19 * 18 = 6,840
So there are 6,840 ways to select a committee of 3 students, where one student is the president, one is the vice-president, and one is the secretary.
For such more questions on Class
https://brainly.com/question/26668139
#SPJ4
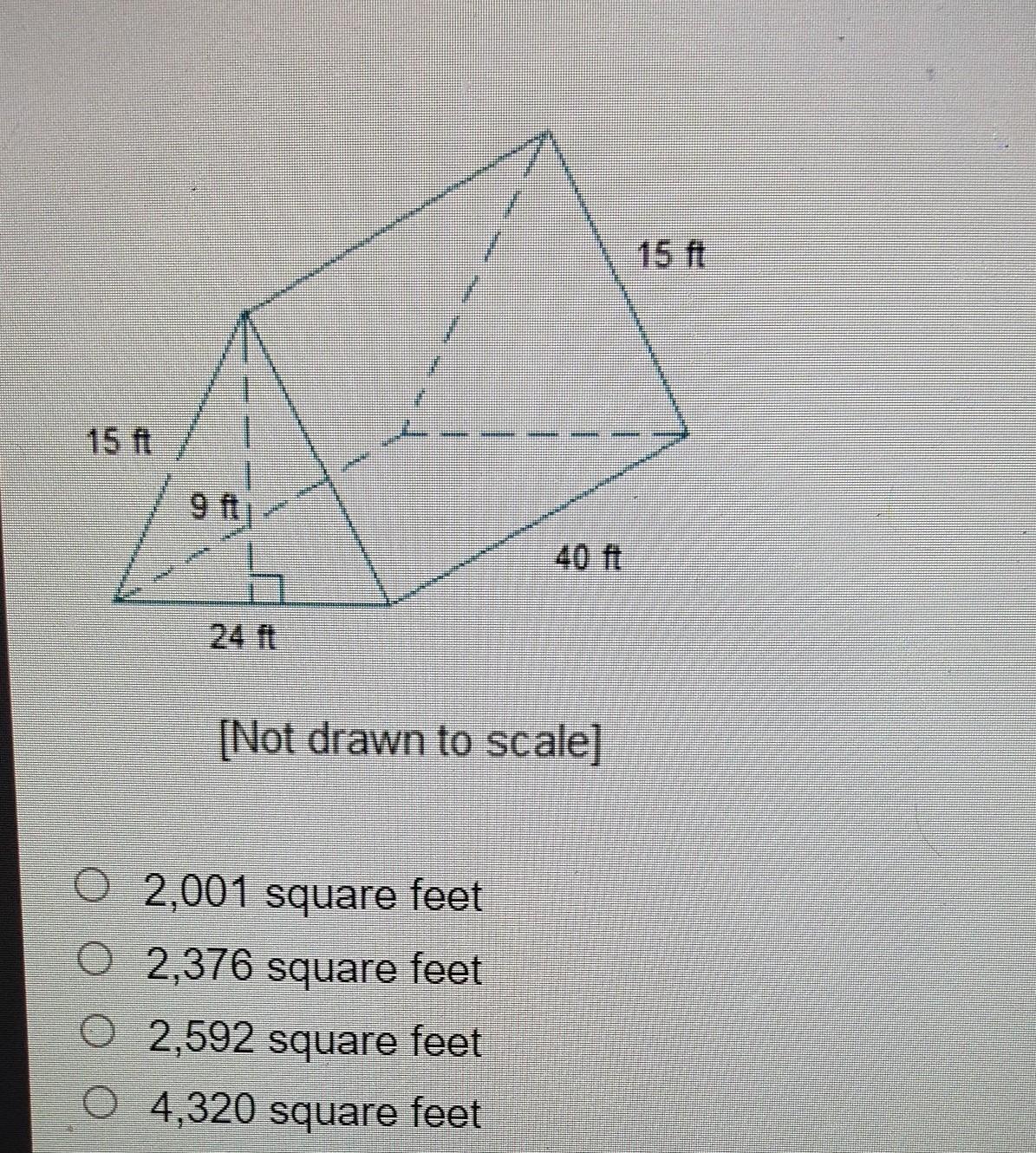
What is the surface area of the triangular prism?
Answers
Answer:
The surface area of the prism is A prism=204m2Step-by-step explanation:
Area is the space that is contained in a two-dimensional figure.
Surface area is the total area of all of the sides and faces of a three-dimensional figure.
To find the surface area, the area of each face is calculated and then add these areas together.
To find the area of a rectangle, multiply the length by the width .
From the graph the length of the rectangle is 10 m and the width is 8 m. Therefore, the area of the bottom face is
From the graph the length of the rectangle is 10 m and the width is 5 m. Therefore, the area of one of the rectangular side faces is
To find the area of a triangle use the following formula where b is the base and h is the height.
From the graph the base of the triangle is 8 m and the height is 3 m. Therefore, the area of one of the triangular faces is
The surface area of the prism is the sum of the area of the bottom face, the area of the two rectangular side faces, and the area of the two triangular faces
brain liest me plsKala wants to burn a total of 600 calories. So far, she has burned 438.7 calories. How many more calories must Kala burn?
Answers
Answer:
Kala needs to burn 161.3 more calories.
Step-by-step explanation:
600 - 438.7 = 161.3
I need to know the answer for geometry

Answers
Answer:
the answer for this will be option c or option 3
−4 4/5÷4 i need a good answer so who can get it will get 10 credits
Answers
Answer:
we use BODMAS
-4 x 4 /5÷ 4=-16/5÷4
=-16÷1\(1/4\)
=-16 ÷ 5/4
=-16 x 4/5
=-64/5
=12\(4/5\)
Step-by-step explanation:
let f = x3i y3j z3k. evaluate the surface integral of f over the unit sphere.
Answers
The surface integral of f over the unit sphere is (4π/15) (3 k), where k is the unit vector in the z-direction. The answer is independent of the specific parameterization of the sphere and only depends on the surface itself.
To evaluate the surface integral of f over the unit sphere, we need to use the formula:
∫∫S f · dS = ∫∫R f(φ,θ) · ||r(φ,θ)|| sin(φ) dφdθ
Where S is the surface of the unit sphere, R is the region in the parameter domain (φ,θ) that corresponds to S, ||r(φ,θ)|| is the magnitude of the partial derivative of the position vector r(φ,θ), and sin(φ) is the Jacobian factor.
For the unit sphere, we have:
x = sin(φ) cos(θ)
y = sin(φ) sin(θ)
z = cos(φ)
So, we can find the partial derivatives:
r_φ = cos(φ) cos(θ) i + cos(φ) sin(θ) j - sin(φ) k
r_θ = -sin(φ) sin(θ) i + sin(φ) cos(θ) j
Then, we can compute the magnitude:
||r_φ x r_θ|| = ||sin(φ) cos(φ) cos(θ) j + sin(φ) cos(φ) sin(θ) (-i) + sin^2(φ) k|| = sin(φ)
Now, we can substitute into the formula and evaluate the integral:
∫∫S f · dS = ∫0^π ∫0^2π (sin^3(φ) cos^3(θ) i + sin^3(φ) sin^3(θ) j + sin^3(φ) cos^3(φ) k) · sin(φ) dφdθ
= ∫0^π ∫0^2π sin^4(φ) (cos^3(θ) i + sin^3(θ) j + cos^3(φ) k) dφdθ
To integrate over θ, we can use the fact that cos^3(θ) and sin^3(θ) are odd functions, so their integral over a full period is zero. Thus, we get:
∫∫S f · dS = ∫0^π (1/5) sin^5(φ) (3 cos^3(φ) k + 2 sin^3(φ) i + 2 cos^3(φ) j) dφ
= (4π/15) (3 k)
Therefore, the surface integral of f over the unit sphere is (4π/15) (3 k), where k is the unit vector in the z-direction. The answer is independent of the specific parameterization of the sphere and only depends on the surface itself.
Learn more on surface integral here:
https://brainly.com/question/15177673
#SPJ11
What is 17% of 300 pleas help
Answers
I believe the answer is 51!
what I did was 0.17×300 which got me 51 ^^
Jacey has 40 pizzas to sell in the concession stand at a
basketball game. Each pizza has been cut into 8 slices of
equivalent size. In the first hour, Jacey sold 16 3/8 pizzas.
In the second hour, she sold 18 3/4 pizzas. How many
pizzas does Jacey have left to sell?
Answers
Answer:
I think 2
Step-by-step explanation:
cause 3-8 the 4 is a 5 3-5 is 2
Consider a male restroom design with minimum plumbing requirements of 12 water closets and 13 lavatories, which one of the following is closest to the minimum space required with considering urinal substitution? Select one: O a. 222 b. 219 c. 237 d. 249
Answers
none of the provided options (a, b, c, d) appear to be accurate or close to the minimum space required.
To determine the minimum space required for a male restroom design with the given plumbing requirements, we need to consider the minimum space required for water closets and lavatories.
The minimum space required for water closets is typically around 30-36 inches per unit, and for lavatories, it is around 24-30 inches per unit.
Since the design requires a minimum of 12 water closets and 13 lavatories, we can estimate the minimum space required as follows:
Minimum space required for water closets = 12 water closets * 30 inches = 360 inches
Minimum space required for lavatories = 13 lavatories * 24 inches = 312 inches
Adding these two values together, we get a total minimum space requirement of 672 inches.
Among the given options, the closest value to 672 inches is option d) 249. However, this value seems significantly lower than the expected minimum space requirement.
To know more about minimum visit:
brainly.com/question/21426575
#SPJ11
Find the area.
8 m
4 m
7 m
square meters

Answers
Answer:
30 square meters
Answer:
How many square meters is a 7 meter by 8 meter rectangle? Use this easy and mobile-friendly calculator to compute the area of a rectangle given the length of ...
Step-by-step explanation:
find a basis for and the dimension of the solution space of the homogeneous system of linear equations−x y z = 02x − y = 04x − 5y − 6z = 0(a) a basis for the solution space
Answers
To find a basis for the solution space of the homogeneous system of linear equations, we need to find the vectors that satisfy the equations when all the variables (x, y, z) are set to zero.
The given system of equations is:
−x + y + z = 0 ...(1)
2x - y = 0 ...(2)
4x - 5y - 6z = 0 ...(3)
To solve this system, we can use the method of Gaussian elimination.
Performing row operations on the augmented matrix [A|0]:
Row1: −x + y + z = 0
Row2: 2x - y = 0
Row3: 4x - 5y - 6z = 0
We can eliminate x from Row2 and Row3 by multiplying Row1 by 2 and adding it to Row2, and multiplying Row1 by 4 and adding it to Row3:
Row1: −x + y + z = 0
Row2: 0x + 3y + 2z = 0
Row3: 0x + y - 2z = 0
Simplifying Row2 and Row3:
Row2: 3y + 2z = 0
Row3: y - 2z = 0
Now we can express y and z in terms of a parameter:
y = -2z
z = t (where t is the parameter)
Substituting these values back into Row1:
−x + (-2z) + z = 0
−x - z = 0
x = -t
Therefore, the solutions to the system of equations can be expressed as:
x = -t
y = -2z
z = t
In vector form, the solutions can be written as:
[ x , y , z ] = [ -t , -2z , t ] = t [ -1 , 0 , 1 ] + z [ 0 , -2 , 0 ]
Now we have two vectors that span the solution space:
v1 = [ -1 , 0 , 1 ]
v2 = [ 0 , -2 , 0 ]
The basis for the solution space is { v1, v2 }. Since we have two linearly independent vectors, the dimension of the solution space is 2.
To learn more about homogeneous system: -brainly.com/question/32516576
#SPJ11
The given homogeneous system of linear equations can be represented as a matrix equation AX = 0, where A is the coefficient matrix and X is the column vector of variables.
To find a basis for the solution space, we can perform row reduction on the augmented matrix [A|0] and identify the pivot columns. The variables corresponding to the non-pivot columns form a basis for the solution space. In this case, the solution space is one-dimensional.
The given homogeneous system of linear equations can be represented in matrix form as:
| -1 1 1 | | x | | 0 |
| 2 -1 0 | * | y | = | 0 |
| 4 -5 -6 | | z | | 0 |
We construct the augmented matrix [A|0]:
| -1 1 1 | 0 |
| 2 -1 0 | 0 |
| 4 -5 -6 | 0 |
Next, we perform row reduction on the augmented matrix to find the row echelon form:
| 1 -1 -1 | 0 |
| 0 -3 -2 | 0 |
| 0 0 0 | 0 |
From the row echelon form, we observe that the first and second columns are pivot columns (leading 1's), while the third column is a non-pivot column.
Let's denote the variables x, y, and z as x = t, y = s, and z = r, where t, s, and r are arbitrary scalars.
From the row echelon form, we have the equations:
x - y - z = 0 (equation 1)
-3y - 2z = 0 (equation 2)
Substituting the values of y and z in terms of s and r from equation 2 into equation 1:
x = y + z = s + r
Hence, the solution to the system is given by x = s + r, y = s, and z = r.
We can express this solution in vector form as X = s * [1, 1, 0] + r * [1, 0, 1], where s and r are scalars.
Therefore, the solution space of the homogeneous system is spanned by the vectors [1, 1, 0] and [1, 0, 1]. Since these two vectors are linearly independent, they form a basis for the solution space. Thus, the dimension of the solution space is 2.
To learn more about homogeneous system: -brainly.com/question/30504189
#SPJ11
4(3+1/4c-1/2a)=?
I need help please :)
Answers
Answer:
Step-by-step explanation:
Distribute the 4 to each term inside of the parentheses.
\(4(3+\frac{1}{4} c-\frac{1}{2} a)=12+c-2a\)
(10 points) Let G(x) = e' - 3x on the interval (-1,3). Find the absolute maximum and absolute minimum value of G on the given interval.
Answers
To find the absolute maximum and absolute minimum values of the function G(x) = e^x - 3x on the interval (-1, 3), we need to examine the critical points and the endpoints of the interval.
Step 1: Find the critical points:
The critical points occur when the derivative of G(x) is equal to zero or is undefined. Let's find the derivative of G(x):
G'(x) = e^x - 3
To find the critical points, we set G'(x) = 0 and solve for x:
e^x - 3 = 0
e^x = 3
x = ln(3)
Step 2: Check the endpoints:
We need to evaluate the function G(x) at the endpoints of the interval (-1, 3), which are -1 and 3.
Step 3: Compare the function values:
Now, we compare the values of G(x) at the critical points and the endpoints to determine the absolute maximum and minimum.
G(-1) = e^(-1) - 3(-1) = e^(-1) + 3
G(3) = e^(3) - 3(3) = e^(3) - 9
G(ln(3)) = e^(ln(3)) - 3ln(3) = 3 - 3ln(3)
We compare these values to find:
Absolute maximum value: G(3) = e^(3) - 9
Absolute minimum value: G(ln(3)) = 3 - 3ln(3)
Therefore, the absolute maximum value of G on the interval (-1, 3) is e^(3) - 9, and the absolute minimum value is 3 - 3ln(3).
To learn more about derivative : brainly.com/question/25324584
#SPJ11
Can someone help me pls

Answers
Answer:
c = (E/m)^1/2
Step-by-step explanation:
Here, we want to solve for c in the given equation
what we have here is that;
E = m•c^2
Thus;
c^2 = E/m
So we have
c^2(*1/2) = (E/m)^1/2
c = (E/m)^1/2
The probability of a drawing a blue marble from a box of 18 marbles is 2/3. How many green marbles should be added to the box in order to reduce the probability to 1/2?
Answers
Answer:
6 green marbles should be added.
Step-by-step explanation:
If the probability of drawing a blue marble from 18 marbles is 2/3 then there are 12 blue marbles because 18 times 2/3 is 12. This means that to reduce this probability to 1/2 you need to add 6 more marbles to the total amount to get it to 24. Now the probability of getting a blue marble is 12/24 which is 1/2.
an hyperboloid is a 3d shape whose cross sections are hyperbolas. a nuclear cooling tower is in the shape of a portion of a hyperboloid. a cross section of the cooling tower can be modeled by the hyperbola shown below, centered at the origin and opening left/right. if the smallest diameter of the cooling tower is 180 m and the diameter is 195 m at its highest point, 80 m above, write the equation of the hyperbola.
Answers
The equation of the hyperbola for the cross section of the cooling tower is x²/8100 - y²/9506.25 = 1.
We must take into account its characteristics in order to formulate the hyperbola's equation for the cooling tower's cross section.
Since the origin serves as the hyperbola's centre, its coordinates are (0, 0).
The left/right opening of the hyperbola indicates that the primary axis is horizontal.
The cooling tower's smallest diameter is 180 metres, which is the same length as the minor axis.
The primary axis' 195 m length and the diameter at its highest point are matched.
The hyperbola's highest point is 80 metres above the centre.
These characteristics allow us to write the hyperbola's equation in standard form:
(x - h)²/a² - (y - k)²/b² = 1
Where (h, k) represents the center of the hyperbola.
Substituting the given values:
Center: (h, k) = (0, 0)
Minor axis: 2a = 180 m, so a = 90 m
Major axis: 2b = 195 m, so b = 97.5 m
Vertical shift: c = 80 m
Now we can write the equation of the hyperbola:
x²/90² - y²/97.5² = 1
Simplifying, we have:
x²/8100 - y²/9506.25 = 1
To learn more about hyperbola link is here
brainly.com/question/19989302
#SPJ4