What is the value of the quantity negative one sixth cubed all raised to the power of negative 3? 10,077,696 1 −1 −10,077,696
Answers
Answer:-20 238
Step-by-step explanation:
Answer: The answer is not that
Step-by-step explanation:
The answer would be 1.
Related Questions
Which equation will let you solve for jk
cos[63] = jk/8
Tan [63]= jk/8
Sin[63]=jk/8
Tan[63]= 8/jk
![Which equation will let you solve for jkcos[63] = jk/8Tan [63]= jk/8Sin[63]=jk/8Tan[63]= 8/jk](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/KFb3BiqxeJH7DxlAM1GGg0nFzPOjjwAL.png)
Answers
In a right triangle, the ratio of the opposite side of one angle to the hypotenuse is called sine.
In this problem the side JK is the opposite side of angle JLK whose value is 63 degrees. The hypotenuse is JL whose value is 8.
So the sine ratio of angle JLK would be
sin L=JK/JL
Substituting the numerical values,
sin 63°=JK/8
This implies JK=sin 63°×8 from wich we will get the value of JK
So, this equation sin 63°=JK/8 will let us solve for jk and the answer is the third one.
Answer:
C
Step-by-step explanation:
mrs wu spent 1/6 of her on a dress and 2 blouses. the dress cost 3 times as much as each blouse. mrs wu spent 3/4 of her remaining money on a watch. she spent $220.50 more on the watch than on the dress.
Answers
Mrs. Wu initially had $1062.40.
Let's break down the given information step by step:
1. Mrs. Wu spent 1/6 of her money on a dress and 2 blouses.
Let's assume Mrs. Wu's total money is represented by the variable M. She spent 1/6 of M on the dress, which means she spent (1/6)M on the dress and the same amount on two blouses.
2. The dress cost 3 times as much as each blouse.
Let's assume the cost of each blouse is represented by the variable B. Therefore, the cost of the dress would be 3B.
3. Mrs. Wu spent 3/4 of her remaining money on a watch.
After spending on the dress and blouses, Mrs. Wu has (M - (1/6)M) = (5/6)M remaining. She spent 3/4 of this remaining money on a watch, which is (3/4) * (5/6)M = (15/24)M.
4. She spent $220.50 more on the watch than on the dress.
The amount spent on the watch is (15/24)M, and the amount spent on the dress is (1/6)M. The difference between these amounts is $220.50.
To find the value of M, we can set up an equation:
(15/24)M - (1/6)M = $220.50
Simplifying the equation:
(15/24 - 1/6)M = $220.50
(5/24)M = $220.50
Multiplying both sides by (24/5):
M = $220.50 * (24/5)
M = $1062.40
for more search question initially
https://brainly.com/question/28162977
#SPJ8
Simon drove 55 miles per hour for 4 hours then 65 miles per hour for 3 hours how far did Simon drive in all
Answers
Answer:
415 miles
Step-by-step explanation:
Start with the speed equation:
speed = distance/time
Now solve the speed equation for distance:
distance = speed × time
Apply the speed equation solved for distance to the two parts of the trip.
4 hours at 55 mph:
distance = 55 mph × 4 hours = 220 miles
3 hours at 65 mph:
distance = 65 mph × 3 hours = 195 miles
Add the two distances to find the total distance:
total distance = 220 miles + 195 miles = 415 miles
Answer: 415 miles
Answer:
415 miles
Step-by-step explanation:
Simon drove 55 miles per hour for 4 hours then 65 miles per hour for 3 hours.
How far did he drive?
d=rt
For the first part of the trip:
d = 55 * 4 = 220 miles
For the second part of the trip:
d = 65*3 =195 miles
Add the miles together
220+195 = 415 miles
Statistics negative numbers and subtraction in a modular arithmetic system

Answers
Solution
(a)
\(\begin{gathered} let\text{ the unknown be x} \\ -7=x(mod\text{ 6\rparen} \\ multiples\text{ of 6 are 6, 12, 18,...} \\ Thus,\text{ } \\ -7(mod\text{ 6\rparen}=-7+12(mod\text{ 6\rparen} \\ =5\text{ mod 6} \\ The\text{ answer = 5} \end{gathered}\)(b)
\(\begin{gathered} 24-25=x(mod\text{ 9\rparen} \\ =-1(mod9)_ \\ Multiples\text{ of 9 are 9, 18, 27, 36,etc} \\ Thus,\text{ } \\ -1(mod\text{ 9\rparen= -1 + 9 \lparen mod 9\rparen} \\ =9=8\text{ \lparen mod 9\rparen} \\ The\text{ answer is 8} \end{gathered}\)HELP I DONT UNDERSTAND :(

Answers
Answer:
{-9,-4,-1}
Step-by-step explanation:
The range is the output values
range = {-9,-4,-1}
Which triangle is a 30-60-90 triangle

Answers
Answer:
I think it's A on edge.
Step-by-step explanation:
Explain why the probability of rolling a sum from 2 to 12 is 100%. [C:2]
Answers
The probability of rolling a sum from 2 to 12 on 2 dices is 100%
Given the data,
The two dice should be rolled.
Now, there are 36 possibilities that might occur while rolling two normal six-sided dice. The reason for this is that when rolling two dice, the total number of outcomes is the product of the numbers of outcomes for each die, and each die has six potential outcomes (numbers 1 through 6).
The resultant 36 results are as follows:
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
2-1, 2-2, 2-3, 2-4, 2-5, 2-6
3-1, 3-2, 3-3, 3-4, 3-5, 3-6
4-1, 4-2, 4-3, 4-4, 4-5, 4-6
5-1, 5-2, 5-3, 5-4, 5-5, 5-6
6-1, 6-2, 6-3, 6-4, 6-5, 6-6
When using two dice, there are a total of 36 possibilities that might occur.
As a result, the results' total ranges from 2 to 12.
Hence , the probability is 100 %
Click here for additional information about probability.
https://brainly.com/question/17089724
#SPJ1
If a(x) = 3x + 1 and p(x)= x-4, what is the domain of (b•a)(x)?
Answers
Answer:
all real numbers
Step-by-step explanation:
Both a(x) and b(x) are polynomials. The set of polynomials is closed on multiplication, so (b•a)(x) will also be a polynomial. All polynomials are defined for all real numbers. The domain is the set of input values (x) for which the function is defined.
The domain of (b•a)(x) is all real numbers.
The measure of angle 1 is 27 degrees.
Complement:
Supplement:
Answers
Answer:
Complement: 63°
Supplement: 153°
Step-by-step explanation:
NOTE: Supplementary angles are two angles that have a sum of 180°. Complementary angles are two angles that have a sum of 90°.
Please mark as brainliest if answer is right
Have a great day, be safe and healthy
Thank u
XD
Evaluate the factorial expression.
19!
16!(3 - 1)!
Answers
Answer:
2907Step-by-step explanation:
19!/16!(3-1)! =16!*17*18*19/16!2! =17*18*19/1*2 = 17*9*19 =2907The 13-year $1,000 par bonds of Vail Inc. pay 13 percent interest. The market's required yield to maturity on a comparable-risk bond is 14 percent. The current market price for the bond is $870.
a. Determine the yield to maturity.
Answers
The current market price for the bond is $870 the yield to maturity is 14.13%
How is yield to maturity calculated?The approximate yield to maturity of this bond is 11.25%, which is above the annual coupon rate of 10% by 1.25%. You can then use this value as the rate (r) in the following formula: C = future cash flows/coupon payments. r = discount rate (the yield to maturity)
knowing that:
Face value (par value) of the bond (F) = $1,000Annual coupon rate (C) = 13% of the face value = 0.13 * $1,000 = $130Years to maturity (n) = 13 yearsCurrent market price of the bond (P) = $870the formula is:
\(P = (C / (1 + r))^1 + (C / (1 + r))^2 + ... + (C + F) / (1 + r)^n\)
Putting the values:
\($870 = (130 / (1 + r))^1 + (130 / (1 + r))^2 + ... + (130 + 1,000) / (1 + r)^13\)
Using the math we find that the percentage is approximately 14.13%;
See more about percentage at brainly.com/question/32197511
#SPJ1
Find the third side in simplest radical form:

Answers
Answer: 53
Step-by-step explanation:
They are both right legs. Use a^2+b^2=c^2.
A= 28^2 B=45^2
A= 784 B= 2025. 2025+ 784= 2809 (radical 2809) To simplified is 53
Suppose IQ scores were obtained for 20 randomly selected sets of siblings . The 20 pairs of measurements yield x overbar equals98.26, y overbar equals99, requals 0.911, P-valueequals 0.000, and ModifyingAbove y with caret equals negative 5.9 plus 1.07 x , where x represents the IQ score of the older child . Find the best predicted value of ModifyingAbove y with caret given that the older child has an IQ of 102 ? Use a significance level of 0.05 g
Answers
Answer:
The answer to the best prediction is 115.04
Step-by-step explanation:
We have to:
x = 102
They also tell us that:
y = 5.9 + 1.07 * x
If we replace we have:
y = 5.9 + 1.07 * (102)
y = 115.04
Therefore, the best predicted value of ModifyingAbove and with caret given that the older child has an IQ of 102 is 115.04
60% of all violent felons in the prison system are repeat offenders. If 32 violent felons are randomly selected, find the following probabilities. Round your answers to 4 decimal places.
a. Exactly 20 of them are repeat offenders.
b. At most 19 of them are repeat offenders.
c. At least 20 of them are repeat offenders.
Answers
determine if the function f(x)=3^(2x-3) is exponential
Answers
An exponential function gives a variable raised to the power of x, where the variable is a positive real number
Yes, \(\underline{f(x) = 3 ^{(2 \cdot x - 3)}}\) is an exponential function
Reason:
An exponential function is a function that can be written in the form;
f(x) = eˣ
Where;
e = Euler's number, which is the number approximately 2.71828
In the general form, an exponential number is a number given in the form;
f(x) = a·bˣ
Where;
b = A positive real number
The given function; \(f(x) = 3 ^{(2 \cdot x - 3)} = \dfrac{3^{2\cdot x}}{3^3} = \dfrac{1}{27} \times 9^x\) is an exponential function
Where;
a = \(\dfrac{1}{27}\)b = 9Therefore, the correct response is; Yes, \(f(x) = 3 ^{(2 \cdot x - 3)}\) is an exponential function
Learn more here:
https://brainly.com/question/17153778
Are the data more spread out below Q1 or above Q3 ? Explain

Answers
Find the sum (9 + 6) (mod 10)
Answers
Answer:
15d10mo
Step-by-step explanation:
Simplify:
(9+6)(mod10)
=15d10mo
In any year, the weather can inflict storm damage to a home. From year to year, the damage is random. Let Y denote the dollar value of damage in any given year. Suppose that in 95% of the years Y = $0, but in 5% of the years Y = $20,000.
A. The mean of the damage in any year is $__. nothing. The standard deviation of the damage in any year is $____.
B. Consider an "insurance pool" of 100 people whose homes are sufficiently dispersed so that, in any year, the damage to different homes can be viewed as independently distributed random variables. Let barY denote the average damage to these 100 homes in a year. The expected value of the average damage barY, is $____. The probability that exceeds $is____.
Answers
Answer:
a. mean = 1000
standard deviation = 4358.9
b. expected value of average damage bar Y = 1000
probability bar y exceeds 2000 = 0.011
Step-by-step explanation:
we have p1 = 95%, y1 = 0, p2 = 5%, y2 = 20000
Mean = (0.95 * 0) + (0.05 * 20000)
= 1000
var(y) = E(y²) - E(Y)²
= we solve for E(y)²
= 0²*0.95 + 20000²*0.05
= 0 + 20000000
then the variance of y = 20000000 - 1000²
=20000000-1000000
= $19000000
standard deviation is the square root of variance
= √19000000
= 4358.9
2.
a. Expected value of average is also the mean = 1000
b. we are to find probability that barY exceeds 2000
\(z=\frac{2000-1000}{\sqrt{19000000/100} }\)
= 1000/435.889
= 2.29
1-p(z≤2.29)
= 1 - 0.989
= 0.011
so the probability that barY exceeds 2000 is 0.011
What is the inverse of the function
f(x) = 121x2 when x > 0?
Answers
Answer:
Step-by-step explanation:the answer is 12x
Let X and Y be discrete random variables and let a and b be constants Which of the following is. FALSE? (a) mean (X + Y) = mean (X) + mean (Y).
Answers
Mean (X + Y) = Mean (X) + Mean (Y).
The above statement is false.
Discrete Random Variable:
A discrete random variable can be defined as a type of variable whose value depends on the numerical outcome of some random phenomenon. Also called a random variable. Discrete random variables are always easily countable integers. A probability mass function is used to describe the probability distribution of a discrete random variable.
Probability Distributions of Discrete Random Variables:
Probability distributions of discrete random variables list the probabilities associated with each possible outcome. Also called probability function or probability mass function.
The probability of a discrete random variable is between 0 and 1. Also, the sum of the probabilities of a discrete random variable is equal to 1. The probability distribution of discrete random variables resembles the normal distribution.
Example:
Suppose two dice are rolled and a random variable X is used to represent the sum of the numbers. The minimum value of X goes from result 1 + 1 = 2 to 2 and the maximum value goes from result 6 + 6 = 12 to 12. Therefore, X can have any value between 2 and 12 (inclusive). If probabilities are assigned to each outcome, we can determine the probability distribution of X.
Discrete random variables should not be confused with algebraic variables. Algebraic variables represent the values of unknown quantities in computable algebraic equations. However, a discrete random variable can have a range of possible values that result from experimentation.
Learn more about Discrete Random Variable:
https://brainly.com/question/12970235
#SPJ4
0.727935 rounded to the nearest thousandths place is
Answers
Answer:
0.728
Step-by-step explanation:
0.727935
The thousandths place is the place with the bold 7, between the 2 and the 9.
To round off to the thousandths place, drop every digit to the right of the 7.
0.727
Now you check the first digit to the right of the 7. If that digit is from 0 to 4, you're done. If the digit is from 5 to 9, you add 1 to the thousandths digit. In this case it is 9, so 7 goes up by 1 and becomes 8.
Answer: 0.728
Simplify by combining like terms. 7x - 5y - 2x - 3 + 5y

Answers
Answer
Option B is correct.
7x - 5y - 2x - 3 + 5y
= 5x - 3
Explanation
To simplify this expression, we will just combine the terms with y, terms with x and the terms without x and y seperately.
7x - 5y - 2x - 3 + 5y
= 7x - 2x - 5y + 5y - 3
= 5x + 0 - 3
= 5x - 3
Hope this Helps!!!
Answer:
\(\sf{5x-3}\)Solution:
Hi! To simplify this expression, what you should do is combine like terms.
\(\begin{gathered}\sf{7x-5y-2x-3+5y}\\\sf{7x-2x-5y+5y-3}\\\underbrace{\sf{5x-3}}_{answer}\end{gathered}\)
Problem solved! It's been a pleasure helping you.
What is the volume of the pyramid? Show all work.
6 m
8 m
4 m
Answers
192/3 = 64
Volume = 64m^3
how to use Lcd in this problem? [a-2. -_1_ =_3_]find Lcd [ a+3 1 a-2]. (a+3)(a+2). multiply all neumerator to (LCD) a-2 - 1= 3 ___ _ a/+3. a+/2 (a-6 )(a+6) - 1 (a+2)(a+3)(a+2/)/*) negative a +positive2: distribuet: (a(a+3)++2. = (a+3)
![how to use Lcd in this problem? [a-2. -_1_ =_3_]find Lcd [ a+3 1 a-2]. (a+3)(a+2). multiply all neumerator](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/9YzZGD9zA9jC2FggrvmnQgEPoiTe27ly.jpeg)
Answers
It's not entirely clear to me what you're trying to solve, but it looks like the initial equation is
\(\dfrac{a-2}{a+3} -1 = \dfrac3{a+2}\)
First convert each term into a fraction with the same (i.e. the least common) denominator. The first term needs to be multiplied by a + 2; the second term by (a + 3) (a + 2); and the third term by a + 3 :
\(\dfrac{a-2}{a+3}\cdot\dfrac{a+2}{a+2} -1\cdot\dfrac{(a+3)(a+2)}{(a+3)(a+2)} = \dfrac3{a+2}\cdot\dfrac{a+3}{a+3} \\\\ \dfrac{(a-2)(a+2)}{(a+3)(a+2)} - \dfrac{(a+3)(a+2)}{(a+3)(a+2)} = \dfrac{3(a+3)}{(a+3)(a+2)}\)
Now that everything has the same denominator, we can combine the fractions into one. Move every term to one side and join the numerators:
\(\dfrac{(a-2)(a+2)-(a+3)(a+2)-3(a+3)}{(a+3)(a+2)} = 0\)
Simplify the numerator:
\(\dfrac{(a^2-4)-(a^2+5a+6)-(3a+9)}{(a+3)(a+2)} = 0 \\\\ \dfrac{-8a-19}{(a+3)(a+2)} = 0\)
If neither a = -3 nor a = -2, we can ignore the denominator:
\(-8a-19 = 0\)
Solve for a :
\(-8a = 19 \\\\ \boxed{a = -\dfrac{19}8}\)
How do I find the possible degree(s) of a function from the graph alone?
Answers
Answer:
To determine the possible degree(s) of a function from the graph alone, you need to examine the behavior of the graph at the extremes (far left and far right) and consider the number of turning points or changes in direction. Here's a step-by-step approach:
Look at the far left side of the graph: Determine the behavior of the graph as it approaches negative infinity. Does the graph approach a specific value, such as a horizontal line (asymptote) or the x-axis? If the graph approaches a horizontal line, it suggests a polynomial function of even degree. If the graph approaches the x-axis, it indicates a polynomial function of odd degree or possibly a function with a root of multiplicity greater than one.
Look at the far right side of the graph: Determine the behavior of the graph as it approaches positive infinity. Similar to step 1, observe if the graph approaches a specific value or a horizontal line. The behavior at the far right side should be consistent with the behavior at the far left side. This can help you identify if the function is even or odd degree.
Examine the number of turning points or changes in direction: Count the number of times the graph changes direction. These points are where the slope of the graph changes from positive to negative or vice versa. The number of turning points can provide an indication of the degree of the polynomial. For example, if there are two turning points, it suggests a polynomial function of degree 3.
Remember that this method provides potential degrees, but it may not definitively determine the exact degree of the function. Additional information or analysis might be required for a more accurate determination.
Andrew is growing tomato plants in his garden. The line plot below shows the
height of each tomato plant on Wednesday.
HEIGHTS OF TOMATO PLANTS
Height (feet)
What was the difference in height between the tallest plant and the shortest
A 1/4 foot
B 2/4 foot
C 3/4 foot
D 4/4 foot
Answers
Answer:
Difference = 2/4
Step-by-step explanation:
Line Plot is a graph that presents data through number line. Here, possible values of considered variable are on number line, & their frequency is denoted by number of dots or crosses above.
As per given line plot for tomato plants heights, 3 plants have height = 1/4, 5 plants have height = 1/2, 4 plants have height = 3/4.
1/4 < 1/2 < 3/4 , 1/4 is the shortest height & 3/4 the longest height of plants. So, difference between smallest & largest height value, ie range = Highest Value - Lowest Value = 3/4 - 1/4 = 2/4

A certain brand of coffee comes in two sizes. An 11.3-ounce package costs $2.88. A 27.8-ounce package costs $6.48.
Find the unit price for each size. Then state which size is the better buy based on the unit price.
Round your answers to the nearest cent.
Answers
Answer:
unit price for 11.3-ounce package = $0.25
unit price for 27.8-ounce package = $0.23
27.8-ounce package is the better buy
Step-by-step explanation:
An 11.3-ounce package costs $2.88. A 27.8-ounce package costs $6.48.
a) 11.3-ounce package
11.3 ounces = $2.88
1 ounce = $2.88 ÷ 11.3
1 ounce = $0.25
b) 27.8-ounce package
27.8 ounces = $6.48
1 ounce = $6.48 ÷ 27.8
1 ounce = $0.23
$0.25 > $0.23
which mixed number is equivalent to the improper fraction of 41/10
Answers
Answer:
4 1/10 when u have a inproper fraction like that every 10 is one whole number
There are four drops of red food coloring in
25 candy canes. How much red food
coloring is in each candy cane
Answers
Answer:
0.16 drops
Step-by-step explanation:
If there are a total of 4 drops in 25, the amount in each could be represented as 4/25. This results in 0.16, thus 0.16 drops in each candy cane.
If this helped you understand and find the solution brainliest would be much appreciated :)
help me find the slope please
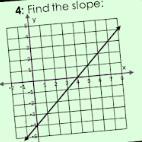
Answers
Answer:
3/4
Step-by-step explanation:
Ok, so I see that the x-intercept is (4,0), while the y-intercept is(-3,0)
Slope is rise/run
Between these two points, the line rose 3 and horizontally went 4 units to the right. Therefore, the slope is 3/4.
Feel free to tell me if I did anything wrong! :)
Also, if you're still confused, I could explain it another way.