What is the value of y? 5,6,or
10
Answers
Answer:
ima say 6
Step-by-step explanation:
Related Questions
Line segment HG
H(-3,-5) & G(2, 2) is dilated
by a factor of 2 to form H'G'.
How long is H'G'?
Answers
The length of HG after the dilation by the factor of 2 is 6.6.
What is the distance between two points ( p,q) and (x,y)?
The shortest distance (length of the straight line segment's length connecting both given points) between points ( p,q) and (x,y) is:
\(D = √[(x-p)² + (y-q)²] D = \sqrt{(x-p)^2 + (y-q)^2} \: \rm units.\)
We are given that;
The points H(-3,-5) & G(2, 2)
Dilation = 2
Now
D^2= (2+3)^2 + (2+5)^2
D^2= 25+49
D^2= 74
D=8.6
After dilation =8.6-2
=6.6
Therefore, the distance by the given dilation will be 6.6
Learn more about distance between two points here:
brainly.com/question/16410393
#SPJ1
4. Would the point (5,10) lie in the solution set of the system of inequalities shown below? Justify your
answer.
x>2
y greater than or equal to 3x - 7
Answers
Point (5,10) is a solution to the system of inequalities.
The system of inequalities is: x > 2y ≥ 3x - 7
Find the point (5,10) lie in the solution set.
To see whether or not (5, 10) is a solution, we need to check whether the point lies in the region bounded by the two inequalities.
In this region, we will test whether
x > 2 and y ≥ 3x - 7 are valid.
So we check both values of x and y:
When x = 5, we have 5 > 2 which is true.
When y = 10, we have 10 ≥ 3(5) - 7 which is also true.
Since both inequalities are true, the point (5,10) lies in the solution set of the system of inequalities.
So, (5,10) is a solution to the system of inequalities.
To know more about inequalities, visit:
https://brainly.com/question/2511777
#SPJ11
An angle of a right triangle measures 65 degrees. If the length of the side opposite to the angle is 20 ft, what are the lengths of the two other sides?
Answers
Answer:
22.07 ft & 9.32 ft
Step-by-step explanation:
by sines rule :
20/sin 65° = r/sin 90° = y/sin 25°
r = 20×sin 90°/sin 65° = 20/0.9063
= 22.07 ft
y = 20×sin 25°/sin 65° =
20× 0.4226/0.9063
= 9.32 ft
Find the slope of the line that passes through (7, 71) and (-100, -1)
Answers
Answer:
72/107
Step-by-step explanation:
We can use the slope formula
m = (y2-y1)/(x2-x1)
= (-1 -71)/(-100-7)
= -72/-107
= 72/107
Katarina bought a package of 500 stickers. 25% of the stickers are hearts. The remaining stickers are stars. Select all the statements that are true.
Answers
Answer: 125 hearts and 375 stars
Step-by-step explanation:
25% of 100 is 25. Take 100 and x it by 5. 100 x 5 is 500 making 25 x 5 125. That being said 125 hearts and 375 stars
Answer:
125 hearts and 375 stars
Step-by-step explanation:
The table below shows the cost in dollars for an
advertiser to have a 30-second commercial run on
television during a football game for four different
years.
Cost of
Commercial
Year
Based on the data in the table, between which two
years was the rate of change in the cost to have a
30-second commercial run on television, in dollars
per year, the greatest?

Answers
According to the information in the table, the highest values are between the first and second year and between the fourth and sixth year.
How to identify in which are the years with the highest increase?To identify the years in which the advertisement has a higher increase. Once we have analyzed the information, we can conclude that the years with the greatest increase were from the first to the second and from the fourth to the sixth. To verify this we must do the following mathematical operations:
2,302,200 - 2,200,000 = 102,2002,400,000 - 2,302,200 = 97,8002,699,963 - 2,400,000 = 299,963Based on the above, we can infer that the years in which it increased the most were from year four to six and from year one to two.
Learn more about price increase at: https://brainly.com/question/13289011
#SPJ1
help pls i have already answered but not sure if my answer is right

Answers
Answer:
China = 6018 / 1339 = 4.49
US = 5093 / 307 = 16.59
Russia = 1704 / 140 = 12.17
India = 1293 / 1157 = 1.12
Japan = 1246 / 127 = 9.81
Germany = 858 / 82 = 10.46
Canada = 614 / 33 = 18.60
a manufacturer knows that their items have a normally distributed length, with a mean of 12.3 inches, and standard deviation of 2.2 inches. if 16 items are chosen at random, what is the probability that their mean length is less than 13.4 inches? (round answer to four decimal places)
Answers
The probability that the mean length is less than 13.4 inches is approximately 0.9998.
To find the probability that the mean length of the 16 randomly chosen items is less than 13.4 inches, we need to use the Central Limit Theorem. According to the Central Limit Theorem, the distribution of sample means approaches a normal distribution as the sample size increases.
First, we need to calculate the standard error of the mean (SE). The formula for SE is:
SE = standard deviation / √sample size
In this case, the standard deviation is 2.2 inches and the sample size is 16. Plugging these values into the formula:
SE = 2.2 / √16
SE = 2.2 / 4
SE = 0.55
Next, we need to calculate the z-score, which measures the number of standard deviations a value is from the mean. The formula for the z-score is:
z = (x - mean) / SE
In this case, the value we are interested in is 13.4 inches, the mean is 12.3 inches, and the SE is 0.55. Plugging these values into the formula:
z = (13.4 - 12.3) / 0.55
z = 2 / 0.55
z ≈ 3.64
Finally, we need to find the probability associated with the z-score using a standard normal distribution table or calculator. The probability of the mean length being less than 13.4 inches is the probability to the left of the z-score of 3.64.
Looking up the z-score of 3.64 in a standard normal distribution table, we find the probability to be approximately 0.9998.
So, the probability that the mean length is less than 13.4 inches is approximately 0.9998.
The probability that the mean length of the 16 randomly chosen items is less than 13.4 inches is approximately 0.9998.
To know more about standard deviation, visit:
brainly.com/question/13498201
#SPJ11
what does x mean in algebra?
Answers
Answer:
The letter "x" is often used in algebra to mean a value that is not yet known. It is called a "variable" or sometimes an "unknown". In x + 2 = 7, x is a variable, but we can work out its value if we try! A variable doesn't have to be "x", it could be "y", "w" or any letter, name or symbol.
Step-by-step explanation:
It is called a "variable" or sometimes an "unknown"
What is variable?A variable is an abstract storage location paired with an associated symbolic name, which contains some known or unknown quantity of information referred to as a value; or in simpler terms, a variable is a named container for a particular set of bits or type of data.
here, we have,
The letter "x" is often used in algebra to mean a value that is not yet known.
It is called a "variable" or sometimes an "unknown".
In x + 2 = 7, x is a variable, but we can work out its value if we try!
A variable doesn't have to be "x", it could be "y", "w" or any letter, name or symbol.
Hence, x is called a "variable" or sometimes an "unknown".
To learn more on variable click:
https://brainly.com/question/19585043
#SPJ2
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
= -x + 2. Find the remaining vertices
PERSEVERE A quadrilateral in the coordinate plane has exactly two lines of symmetry, y = x-1 and y
of the figure if there is a vertex at (-1,0). Graph the figure and the lines of symmetry on a separate sheet of paper.
List the coordinates of the vertices by starting with the vertex at (-1,0) and moving clockwise around the quadrilateral.
Answers
Answer:
wheres the photo?
Step-by-step explanation:
1. A Better Golf Tee? An independent golf equipment testing facility compared the difference in the performance of golf balls hit off a brush tee to those hit off a 4 yards more tee. A'Air Force One D
Answers
Overall, the testing facility concluded that the brush tee would be a better option for golfers looking to improve their drives.
An independent golf equipment testing facility compared the difference in the performance of golf balls hit off a brush tee to those hit off a 4 yards more tee. A'Air Force One DFX driver was used to hit the balls, with an average swing speed of 100 miles per hour. The testing facility wanted to determine which tee would perform better and whether it would be beneficial to golfers to switch to a different tee.
The two different types of tees were the brush tee and the 4 Yards More tee. The brush tee is designed with bristles that allow the ball to be suspended in the air, minimizing contact between the tee and the ball. This design is meant to reduce spin and allow for longer and straighter drives. On the other hand, the 4 Yards More tee is designed to be more durable than traditional wooden tees, and its design is meant to create less friction between the tee and the ball, allowing for longer drives.
The testing results showed that the brush tee was able to create longer and straighter drives than the 4 Yards More tee. This is likely due to the brush tee's design, which allows for less contact with the ball, minimizing spin and creating longer and straighter drives.
To Know more about average visit:
https://brainly.com/question/24057012
#SPJ11
Hellllllllllllllllllllllllllllllllpppppppppppppppppppppppppppp mmmmmeeeeee

Answers
help pt.idk lol plzz

Answers
Step-by-step explanation:
15 x 3 = 45
13 x 3 = 39
So
45 ÷ 3 = 15
39 ÷ 3 = 13
36 ÷ 3 = 12
X=12
suppose that you watch the game show over many years and find that door 1 hides the car 50% of the time, door 2 has the car 40% of the time, and door 3 has the car 10% of the time. what then is your optimal strategy? in other words, which door should you pick initially, and then should you stay or switch? what is your probability of winning with the optimal strategy? explain.
Answers
The optimal strategy is to pick door 1 and stay - this will give you a 50 percentage chance of winning the car.
The optimal strategy to win the game show is to pick door 1 initially and stay. This is because door 1 has the car 50% of the time, which is the highest chance of any of the three doors. If you switch to a different door, then you would have a 40% chance of winning if you switched to door 2, and a 10% chance of winning if you switched to door 3. Since door 1 has the highest chance of having the car, it is the optimal choice to initially select door 1 and stay. By doing so, you have a 50% chance of winning the car.
Learn more about percentage here
https://brainly.com/question/16797504
#SPJ4
Multiply binomial ( x + 8)(x + 3)
Answers
Given:
( x + 8)(x + 3)
To multiply the binomial, we use FOIL method as shown below:
\((a+b)(c+d)=ac+ad+bc+bd\)So,
\(\begin{gathered} \mleft(x+8\mright)\mleft(x+3\mright)=(x)(x)+(x)(3)+(8)(x)+(8)(3) \\ \text{Simplify} \\ =x^2+3x+8x+24 \end{gathered}\)Next, we collect like terms:
\(\begin{gathered} =x^2+(3x+8x)+24 \\ \text{Simplify} \\ =x^2+11x+24 \end{gathered}\)Therefore, the answer is:
\(x^2+11x+24\)Write an equation that represents the line.
Use exact numbers.

Answers
Answer:
1x-2y
Step-by-step explanation:
You have to go down 2 on the y-axis and over to the right 1 on the x axis
What is the scale factor from triangle ABC to triangle GHI

Answers
Answer:
4
Step-by-step explanation:
(1). A cyclist starts a journey from town A. He rides 10km north, then 5km east and finally 10km on a bearing of 045°. a) How far east is the cyclist's destination from town A? b). How far north is the cyclist's destination from town A? c). Find the distance and bearing of the cyclist's destination from town A (Correct your answers to the nearest km and degree)
Answers
The required answers are a) 17.1 km b) 7.1 km, c) 18.6 km away from town A on a bearing of 293°.
How to find the distance and angle?To solve this problem, we can use vector addition to find the displacement vector from town A to the cyclist's destination.
a) To find how far east the cyclist's destination is from town A, we need to find the east component of the displacement vector. We can break down the displacement vector into its north and east components using trigonometry:
\($$\text{East displacement} = 5\text{ km} + 10\text{ km}\cos(45^\circ) = 5\text{ km} + 10\text{ km}\frac{\sqrt{2}}{2} = 10\text{ km} + 5\sqrt{2}\text{ km} \approx 17.1\text{ km}$$\)
So the cyclist's destination is approximately 17.1 km east of town A.
b) Similarly, to find how far north the cyclist's destination is from town A, we need to find the north component of the displacement vector:
\($$\text{North displacement} = 10\text{ km}\sin(45^\circ) = 10\text{ km}\frac{\sqrt{2}}{2} = 5\sqrt{2}\text{ km} \approx 7.1\text{ km}$$\)
So the cyclist's destination is approximately 7.1 km north of town A.
c) To find the distance and bearing of the cyclist's destination from town A, we can use the Pythagorean theorem and trigonometry. The displacement vector is the hypotenuse of a right triangle with legs of length 17.1 km and 7.1 km, so its length is:
\($$\text{Displacement} = \sqrt{(17.1\text{ km})^2 + (7.1\text{ km})^2} \approx 18.6\text{ km}$$\)
To find the bearing of the displacement vector, we can use the inverse tangent function:
\($$\text{Bearing} = \tan^{-1}\left(\frac{\text{East displacement}}{\text{North displacement}}\right) \approx 67^\circ$$\)
However, this angle is measured clockwise from north, so we need to subtract it from 360° to get the bearing measured counterclockwise from north:
\($$\text{Bearing} = 360^\circ - 67^\circ = 293^\circ$$\)
So the cyclist's destination is approximately 18.6 km away from town A on a bearing of 293°.
To know more about Angle visit:
brainly.com/question/28451077
#SPJ9
A rectangular restaurant kitchen has an area of 80 square meters and a perimeter of 36 meters. What are the dimensions of the kitchen?
Answers
Answer:
Step-by-step explanation
Frist, the area = ab = 30 m^2 and the perimeter = 2(a + b) = 34 m or a + b = 17 m (2). Solving (1) and (2), a = 15 m and b = 2 m. Since it is a rectangle, the dimensions are (all in m) so the answer is: 15, 2, 15, 2.
Answer:
THe kitchen is 8 by 10
Step-by-step explanation:
x = width
y = length
Area = xy = 80 m²
Perimeter = 2x + 2y = 36 m
2x = 36 - 2y
x = 18 - y substitute into equation 1
(18 - y)(y) = 80
-y² + 18y - 80 = 0 find roots of y by factoring
y² - 18y + 80 = 0
(y - 8)(y - 10) = 0
y = 8, 10
Since xy = 80, then:
x = 80/10 = 8, or, x = 80/8 = 10
Now you have your dimensions: 8 and 10
To check the answers:
8 x 10 = 80 m²
2(8) + 2 (10) = 36 m
Answers are correct!
Find the exact value of each trigonometric expression.
1)cot 30
2)csc pi/4
Please show step by step, thanks!:D
Answers
Step-by-step explanation:
1) Cotangent is cosine over sine.
From unit circle, cos 30° = ½√3 and sin 30° = ½
cot 30° = cos 30° / sin 30°
cot 30° = (½√3) / ½
cot 30° = √3
2) Cosecant is the inverse of sine.
From unit circle, sin π/4 = 1/√2
csc π/4 = 1 / sin π/4
csc π/4 = 1 / (1/√2)
csc π/4 = √2
Can someone help me I don't know

Answers
Answer:
The answer would be (x-5, y-5)
Step-by-step explanation:
You can find this out by finding the difference between D(3,5) and D'(-2,1) (pr any other coordinate) which is -5 in both the x and y coordinates making the answer (x-5, y-5).
(3-4^2)^2+8
Bdhdhdhsjsjsj
Answers
Answer: 177
Step-by-step explanation:
1. 4x4=16
(3-16)^2+8
2. 3-16=-13
(-13)^2+8
3. -13x-13=169
169+8
4.169+8=177
177
Answer:
177
Step-by-step explanation:
PEMDAS
The PEMDAS rule is an acronym representing the order of operations in math:
ParenthesesExponentsMultiplication and Division (from left to right)Addition and Subtraction (from left to right)Given expression:
\((3-4^2)^2+8\)
Parentheses
Begin by calculating the part inside the parentheses.
Following PEMDAS, calculate the exponent first:
\(\implies (3-4^2)^2+8=(3-16)^2+8\)
Then carry out the subtraction:
\(\implies (3-16)^2+8=(-13)^2+8\)
Exponents
\(\textsf{Apply the exponent rule}: \quad (-a)^n=a^n, \quad \textsf{if }n \textsf{ is even}\)
\(\implies (-13)^2+8=169+8\)
Addition
\(\implies 169+8=177\)
Therefore:
\(\implies (3-4^2)^2+8=177\)
Genghis Motors wants to build cars and motorbikes on a budget. The company plans to spend at most $75000
and use at least 320 workers to build cars and motorbikes.
8000C + 5500M < 75000 represents the number of cars C and motorbikes M the company can build by
spending at most $ 75000.
52C + 38M > 320 represents the number of cars and motorbikes the company can build by using at least
320 workers.
Can the company meet both of its expectations by building 4 cars and 6 motorbikes?

Answers
Answer:
52 + 38,000,000 = 38000052- 75000= 37999977
Step-by-step explanation:
52 + 38M The 320 Is Just A Distraction Don't worry about that then subtract 75000 and that is how you do it
A line passing through which of the following pairs of coordinates represents a proportional relationship? A. (1, 3) and (2, 6) B. (1, 1) and (1, 3) C. (1, 2) and (2, 3) D. (1, 3) and (3, 6)
Answers
Answer:
Answer is A - (1, 3) and (2, 6)
Step-by-step explanation:
(1, 3) • 2
= (1 • 2, 3 • 2)
= (2, 6)
Ratio: 2/2, 6/2
Therefore, the answer is A.
Answer:
a
Step-by-step explanation:
u = [0], v = [5], w = [-1]
[2] [4] [0]
[1] [3] [3]
(a) Calculate the cross product of u x v. (b) Calculate the area size of the parallelogram () with sides u and v. (c) Calculate the volume of the parallelepiped () with sides u, v and W.
Answers
(a) The cross product of u x v is [-15, 15, -8]. (b) The area size of the parallelogram is approximately 27.18. (c) The volume of the parallelepiped is -24.
(a) To calculate the cross product of u x v, we can use the formula:
u x v = [u₂v₃ - u₃v₂, u₃v₁ - u₁v₃, u₁v₂ - u₂v₁]
Substituting the values of u and v, we have:
u x v = [0*4 - 3*5, 3*5 - 0*2, 0*2 - 2*4]
= [-15, 15, -8]
Therefore, the cross product of u x v is [-15, 15, -8].
(b) To calculate the area size of the parallelogram with sides u and v, we can use the magnitude of the cross product:
Area = ||u x v||
Substituting the values of u x v calculated in part (a), we have:
Area = ||[-15, 15, -8]|| = sqrt((-15)^2 + 15^2 + (-8)^2) = sqrt(450 + 225 + 64) = sqrt(739) ≈ 27.18
Therefore, the area size of the parallelogram is approximately 27.18.
(c) To calculate the volume of the parallelepiped with sides u, v, and w, we can use the scalar triple product:
Volume = u · (v x w)
Substituting the values of u, v, and w, we have:
Volume = [0, 3, 0] · ([-15, 15, -8] x [-1, 3, 0])
Using the cross product formula from part (a) for the cross product of [-15, 15, -8] x [-1, 3, 0], we have:
Volume = [0, 3, 0] · [-24, -8, -90]
= 0*(-24) + 3*(-8) + 0*(-90)
= -24
Therefore, the volume of the parallelepiped is -24.
To know more about volume and area, click here: brainly.com/question/13789496
#SPJ11
An investment of $10,000 earns interest at an annual rate of 6. 7% compounded continuously. Answer Part 1 and Part 2 with this information.
Part 1:
Find the instantaneous rate of change in the amount in the account after 2 years (in dollars per year). Round to the nearest cent.
$____per year.
Part 2
Find the instantaneous rate of change in the amount in the account at the time the amount is equal to $14,101. Round to the nearest cent.
$_____per year
Answers
1. The instantaneous rate of change in the amount after 2 years is \($1,605.64\) per year
2. The instantaneous rate of change in the amount at the time the amount is equal to \($14,101\) is approximately $994.78 per year
\(A = P\)× \(e^{rt}\)
where P is the principal (initial investment), r is the annual interest rate as a decimal, and t is the time in years.
For this problem, we have P = $10,000, r = 0.067 (6.7% as a decimal), and we want to find the instantaneous rate of change in the amount after 2 years, so t = 2.
Part 1:
To find the instantaneous rate of change, we need to take the derivative of the function A(t) with respect to t:
\(dA/dt = Pre^{rt}\)
At\(t = 2\), we have:
\(A(2) = $10,000e^{0.0672}\)
\(= $11,868.94\)
\(dA/dt = $10,0000.067e^{0.067}\)×\(2)\)
\(= $1,605.64\)
So the instantaneous rate of change in the amount after 2 years is $1,605.64 per year
Part 2:
To find the time at which the amount in the account is $14,101, we need to solve the equation A = $14,101 for t:
\($14,101\)\(= $10,000\) × \(e^{0.067t}\)
Dividing both sides by $10,000:
\(1.4101 = e^{0.067t}\)
Taking the natural logarithm of both sides:
\(ln(1.4101) = 0.067t\)
Solving for t:
\(t = ln(1.4101)/0.067\)
≈ \(3.5 years\)
So the time at which the amount in the account is $14,101 is approximately 3.5 years.
To find the instantaneous rate of change at this time, we need to evaluate the derivative at t = 3.5:
\(dA/dt = $10,0000.067e^{0.067}\)×\(3.5)\)
≈ \($994.78\)
So the instantaneous rate of change in the amount at the time the amount is equal to $14,101 is approximately $994.78 per year
Compound interest is the interest you earn on interest. This can be illustrated by using basic math: if you have $100 and it earns 5% interest each year, you'll have $105 at the end of the first year. At the end of the second year, you'll have $110.25
To know more about compound interest visit:
https://brainly.com/question/29335425
#SPJ4
HELP NEEDED ASAP THANKS

Answers
Answer:
{A) X=5} {B) X=2.75}
Step-by-step explanation:
A) (2)4x-1/2=x+7(2) - multiply each side by denominator
4x-1=x+14
-x + 1 -x +1
3x=15
÷3. ÷3
x=5
B) (2)3x+2=2x+13/2(2)
6x+2=2x+13
-2x -2. -2x -2
4x=11
÷4. ÷4
x=2.75
Answer:
x = 7.5 , x = 1
Step-by-step explanation:
(a)
\(\frac{4x-1}{2}\) = x + 7 ( multiply both sides by 2 to clear the fraction )
4x - 1 = 2(x + 7)
4x - 1 = 2x + 14 ( subtract 2x from both sides )
2x - 1 = 14 ( add 1 to both sides )
2x = 15 ( divide both sides by 2 )
x = 7.5
(b)
3x + 2 = \(\frac{2x+13}{3}\) ( multiply both sides by 3 to clear the fraction )
3(3x + 2) = 2x + 13
9x + 6 = 2x + 13 ( subtract 2x from both sides )
7x + 6 = 13 ( subtract 6 from both sides )
7x = 7 ( divide both sides by 7 )
x = 1
the data below represents the number of t-shirts sold per week by a student who started his own online t-shirt business. find the weighted mean of the number of t-shirts sold per week. (round your answer to the nearest tenth if necessary.) t-shirts sold per week frequency 4 7 8 5 12 4 16 1 weighted mean
Answers
The weighted weekly mean of t-shirt sales is 5.6.
The total number of weeks reported is the sum of the frequency column.
1+4+7+3 = 15 weeks
The total number of t-shirts sold is calculated as the product of the quantity of t-shirts sold and the number of weeks during which those t-shirts were sold.
2*1 + 4*4 + 6*7 + 8*3 = 2 + 16 + 42 + 24 = 84
The weighted mean, which is the product of the total quantity of t-shirts and the total number of weeks, represents the average number of T-shirts sold every week:
84/15 = 5.6
Response: 5.6
Learn more about mean here
https://brainly.com/question/15323584
#SPJ4
What’s the answer for 8
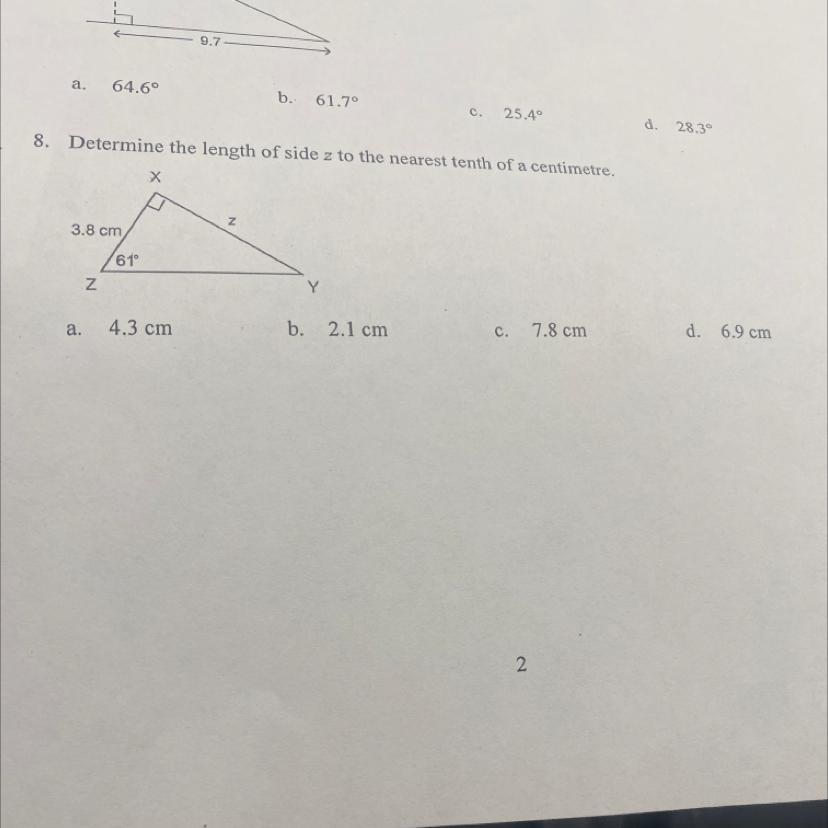
Answers
Answer:
Z=6.855 cm
Step-by-step explanation:


