What letter comes next in this pattern A,F,L,S
Answers
Related Questions
A professor knows that her statistics students' final exam scores have a mean of 79 and a standard deviation of 11.3. In his class, an "A" is any exam score of 90 or higher. This quarter she has 22 students in her class. What is the probability that 6 students or more will score an "A" on the final exam?
prob =
Answers
0.1449 = 14.49% probability that 6 students or more will score an "A" on the final exam.
---------------
For each student, there are only two possible outcomes. Either they score an A, or they do not. The probability of a student scoring an A is independent of any other student, which means that the binomial probability distribution is used to solve this question.
Additionally, to find the proportion of students who scored an A, the normal distribution is used.
----------------
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of a success.
----------------
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean and standard deviation , the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
----------------
Proportion of students that scored an A:
Scores have a mean of 79 and a standard deviation of 11.3, which means that \(\mu = 79, \sigma = 11.3\)
Scores of 90 or higher are graded an A, which means that the proportion is 1 subtracted by the p-value of Z when X = 90, so:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{90 - 79}{11.3}\)
\(Z = 0.97\)
\(Z = 0.97\) has a p-value of 0.8340.
1 - 0.8340 = 0.166
The proportion of students that scored an A is 0.166.
----------------
Probability that 6 students or more will score an "A" on the final exam:
Binomial distribution.
22 students, which means that \(n = 22\)
The proportion of students that scored an A is 0.166, which means that \(p = 0.166\)
The probability is:
\(P(X \geq 6) = 1 - P(X < 6)\)
In which
\(P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)\)
Then
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{22,0}.(0.166)^{0}.(0.834)^{22} = 0.0184\)
\(P(X = 1) = C_{22,1}.(0.166)^{1}.(0.834)^{21} = 0.0807\)
\(P(X = 2) = C_{22,2}.(0.166)^{2}.(0.834)^{20} = 0.1687\)
\(P(X = 3) = C_{22,3}.(0.166)^{3}.(0.834)^{19} = 0.2239\)
\(P(X = 4) = C_{22,4}.(0.166)^{4}.(0.834)^{18} = 0.2117\)
\(P(X = 5) = C_{22,5}.(0.166)^{5}.(0.834)^{17} = 0.1517\)
Then
\(P(X < 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 0.0184 + 0.0807 + 0.1687 + 0.2239 + 0.2117 + 0.1517 = 0.8551\)
\(P(X \geq 6) = 1 - P(X < 6) = 1 - 0.8551 = 0.1449\)
Thus
0.1449 = 14.49% probability that 6 students or more will score an "A" on the final exam.
For a problem that used the normal distribution, you can check https://brainly.com/question/15181104, and for a problem that used the binomial distribution, you can check https://brainly.com/question/15557838
In a diagram, ∠A and ∠B are vertical angles, and ∠B is a complementary angle with ∠C. If ∠A=22°, write an equation that you can use to solve for ∠C.
Answers
Answer:
22° + m<C = 90°
Step-by-step explanation:
Pre-SolvingWe are given that <A (which is equal to 22°) and <B are vertical angles, and that <B is complementary to <C.
We want to write an equation that will help us solve <C.
SolvingRecall that vertical angles are congruent by vertical angles theorem.
This means that <A ≅ <B; it also means that the measure of <B is also 22°.
Also recall that complementary angles add up to 90°.
This means that m<B + m<C = 90°.
Since we deduced that m<B is 22°, we can substitute that value into the equation.
Hence, an equation that can be used to solve for <C is:
22° + m<C = 90°
Consider the accompanying matrix as the augmented matrix of a linear system. State in words the next two elementary row operations that should be performed in the process of solving the system
[1 -5 3 0 -2
0 3 -7 0 4
0 0 1 2 -2]
Answers
Answer:
The answer is below
Step-by-step explanation:
The next step to solve the system, would be to divide the second row by 3 and we would be left with: 3 * R2
[1 -5 3 0 -2
0 1 -7/3 0 4/3
0 0 1 2 -2]
Then what we will do is multiply row 3 by 7/3 and then subtract it from row 2, that is, R2 - 7/3 * R3, and it would look like this:
[1 -5 3 0 -2
0 1 0 14/3 -10/3
0 0 1 2 -2]
And these would be the next two steps in the process of solving the system.
13 POINTS AND WILL BE MARKED BRAINLIEST IF CORRECT!

Answers
Answer:
I think its 144!!!!!!!!!!!!!!!!!!
Answer:
Diagram 2 (Bottom diagram)
Step-by-step explanation:
The ratio is twice as many (2)
2:1
Two angles are complementary. One angle measures 60 degrees. What is the measure of the other angle?
I'm not sure if its A.

Answers
Answer:
30
Step-by-step explanation:
Complementary angles add to 90
x+60 = 90
x+60-60 = 90-60
x = 30
Answer: A
Step-by-step explanation:
Complementary angles sum up to 90 degrees. Thus, we can write that:
90=angle1+angle2
90-angle1=angle2
90-60=angle2
angle2=30
A jar contains 8 red marbles, 10 blue marbles, and 2 yellow marbles. One marble is chosen at random. The color is recorded in the table and then it is returned to the jar. This is repeated 40 times. What is the experimental probability of choosing a yellow marble? Express your answer as a percent to the nearest whole number.
RED/14 BLUE/16 YELLOW/10
Answers
Answer:
1/4 or 25%Step-by-step explanation:
Experimental probability:
Pe = number of event occurred / number of attemptsProbability of yellow:
Pe(yellow) = 10/40 = 1/4 = 25%A {(2,1),(4, 1), (6, 1), (8, 1)} 4) Choose the set that is a function. B) {(2,1),(4,3), (6,5), (2,7)} {(2, 1), (4, 1), (2, 5), (4,7)} D) {(2, 1), (2, 3), (2, 5), (2,7)}
Answers
we know that
A function is a binary relation over two sets that associates every element of the first set, to exactly one element of the second set
so
For one value of x there is only one value of y
Verify each options
Option A
The option A is a function
Option B
Is not a function , because we have the points (2,1) and (2,7)
one value of x and there are two values of y
Option C
Is not a function , because we have
(2,1) and (2,5) -----> one value of x and to values of y
(4,1) and (4,7) --> one value of x and to values of y
Option D
Is not a function ------> one value of x and 4 values of y
therefore
the answer is the option A
Consider writing onto a computer disk and then sending it through a certifier that counts the number of missing pulses. Suppose this number x has a Poisson distribution with parameter μ = 0.5. (Round your answers to three decimal places.)
(a) What is the probability that a disk has exactly one missing pulse?
(b) What is the probability that a disk has at least two missing pulses?
(c) lf two disks are independently selected, what is the probability that neither contains a missing pulse?
Answers
Answer:
Explained below.
Step-by-step explanation:
The random variable X is defined as the number of missing pulses and follows a Poisson distribution with parameter (μ = 0.50).
The probability mass function of X is as follows:
\(P(X=x)=\frac{e^{-\mu}\ \mu^{x}}{x!};\ x=0,1,2,3...\)
(a)
Compute the probability that a disk has exactly one missing pulse as follows:
\(P(X=1)=\frac{e^{-0.50}\ 0.50^{1}}{1!}=0.3033\)
Thus, the probability that a disk has exactly one missing pulse is 0.3033.
(b)
Compute the probability that a disk has at least two missing pulses as follows:
\(P(X\geq 2)=1-P(X<2)\\\)
\(=1-[P(X=0)+P(X=1)]\\=1-[\frac{e^{-0.50}\ 0.50^{0}}{0!}+\frac{e^{-0.50}\ 0.50^{1}}{1!}]\\=1-0.6065-0.3033\\=0.0902\)
Thus, the probability that a disk has at least two missing pulses is 0.0902.
(c)
It is provided that the two disks selected are independent of each other.
The probability that a disk has no missing pulses is:
\(P(X=0)=\frac{e^{-0.50}\ 0.50^{0}}{0!}=0.6065\)
Compute the probability that neither of the two disks contains a missing pulse as follows:
\(P(X_{1}=0,\ X_{2}=0)=P(X_{1}=0)\times P(X_{2}=0)\)
\(=0.6065\times 0.6065\\=0.367842\\\approx 0.3678\)
Thus, the probability that neither of the two disks contains a missing pulse is 0.3678.
Suppose you have 100,000 dollars for investment. There are three banks that have different offers to you.
Bank A offers you 4% interest compounded monthly
Bank B offers you simple interest 6%.
Bank C offers you 5% interest compounded yearly.
(a) If you plan to save your money for one year, which bank will you choose?
(b) If you plan to save your money for 5 years, which bank will you choose?Does your opinion change? Why?
(c) If you plan to save your money for 15 years, which bank will you choose? Does your opinion change? Why?
Answers
Answer:
A. I did this one before so yeah!
PLEASE HELP ASAP
solve -1/6[3-15(1/3)2]
![PLEASE HELP ASAP solve -1/6[3-15(1/3)2]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/C0Nx4ldjSdyeTD1pu34mYu8d7IAOliwi.png)
Answers
Answer:
C) -2/9
Step-by-step explanation:
\(\displaystyle -\frac{1}{6}\biggr[3-15\biggr(\frac{1}{3}\biggr)^2\biggr]\\\\=-\frac{1}{6}\biggr[3-15\biggr(\frac{1}{9}\biggr)\biggr]\\\\=-\frac{1}{6}\biggr[3-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{27}{9}-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{12}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{4}{3}\biggr]\\\\=-\frac{4}{18}\\\\=-\frac{2}{9}\)
Answer:
Hence, Option (C) - 2/9 is the Answer:
Step-by-step explanation:
-1/6 [3 -15(1/3)^2]
-1/6(3 -15)(1/9))
-1/6(3 - 5/3)
-1/6 (4/3)
Hence, Option (C) - 2/9 is the Answer:
I hope it helps!
A dairy needs 258 gallons of milk containing 7% butterfat how many gallons each of milk containing 8% butterfat and milk containing 2% butterfat must be used to obtain the desired 258 gallons
Answers
Let's assume x gallons of milk containing 8% butterfat and y gallons of milk containing 2% butterfat are used.
The total amount of milk is x + y gallons, and we want it to be equal to 258 gallons.
To determine the amount of butterfat in the mixture, we can multiply the volume of each type of milk by its respective butterfat percentage and sum them up.
For milk containing 8% butterfat, the amount of butterfat is 0.08x (8% is equivalent to 0.08 as a decimal).
For milk containing 2% butterfat, the amount of butterfat is 0.02y (2% is equivalent to 0.02 as a decimal).
Since we want the final mixture to contain 7% butterfat, we can set up the following equation:
0.08x + 0.02y = 0.07(258)
Simplifying the equation, we have:
0.08x + 0.02y = 18.06
To solve for x and y, we need another equation. Since the total amount of milk is x + y = 258, we can rearrange it to y = 258 - x.
Substituting this value into the equation above, we get:
0.08x + 0.02(258 - x) = 18.06
Solving this equation will give us the values of x and y, which represent the gallons of milk containing 8% butterfat and 2% butterfat, respectively, needed to obtain the desired 258 gallons.
For such more question on gallons
https://brainly.com/question/28274339
#SPJ8
screenshot included below

Answers
Answer:
product A
75%
67%
Product B
Step-by-step explanation:
I just found the percentage by dividing the amount of people who found relief into the whole
Hopes this helps please mark brainliest
The mean life of a new smart LED bulb is 20,000 running hours with a standard deviation is 2,250 hours. The data is normally distributed. If a home improvement store sold 18,000 of these light bulbs in the first year of production, how many light bulbs would you expect to last longer than 22,250 hours?
Answers
Answer: The expected number of bulbs that would last longer than 22,250 hours is approximately 2,857.
Step-by-step explanation:
To solve this problem, we can start by finding the z-score for 22,250 using the formula:z = (x - mean) / standard deviationz = (22,250 - 20,000) / 2,250 = 1Next, we need to find the proportion of bulbs lasting longer than 22,250. We can look up this proportion in a standard normal distribution table or use a calculator, which gives us a probability of 0.1587.Finally, we can use this probability to find the expected number of bulbs that will last longer than 22,250:Expected number of bulbs = probability * total number of bulbs sold Expected number of bulbs = 0.1587 * 18,000 = 2,857Therefore, we can expect that approximately 2,857 of the 18,000 bulbs sold will last longer than 22,250 running hours.
Answer:
the afternoon is the right one
We need help finding the means of the sides of this figure.
(Photo attached)
Thank you

Answers
Answer:
3) 5
4) 8.2
5) 6.8
6)FG = 6.4
7) EF = 3.6
8)DF = 4.8
Step-by-step explanation:
From the attached triangle, using trigonometric ratio we can find ∠G as; tan^(-1) (6/8)
Thus, ∠G = 36.87°
Still using trigonometric ratios;
FG/8 = cos 36.87°
FG = 8 cos 36.87°
FG = 6.4
3) EF + FG = EG
Since EG is 10, mean of EF and FG = 10/2 = 5
4) mean of EG and FG = (10 + 6.4)/2 = 8.2
5) EF + FG = EG
Thus; EF = EG - FG
EF = 10 - 6.4
EF = 3.6
Mean of EG and EF = (10 + 3.6)/2 = 6.8
6) FG = 6.4
7) EF = 3.6
8) Using trigonometric ratio;
DF/8 = sin 36.87
DF = 8 × 0.6
DF = 4.8
Which of the following statements describes a rhombus?A. all sides are equalB. the opposite angles are equalC. the diagonals bisect each other at right anglesD. the adjacent angles are not supplementary
Answers
The Option B statement "the opposite angles are equal" accurately describes a rhombus, as each of the four angles of a rhombus are equal to each other. This means that the opposite sides of the rhombus have the same measure.
Which statement describes a rhombus?B. the opposite angles are equalA rhombus is a four-sided shape with all sides equal in length. It is also known as a diamond shape. The most important thing to remember about a rhombus is that the opposite angles are equal.
This means that the two angles across from each other on the rhombus have the same measure. This is what is meant by the statement "the opposite angles are equal," and it accurately describes a rhombus.
Learn more about Geometry: https://brainly.com/question/24375372
#SPJ4
A trapezoid is a quadrilateral with one or more pairs of parallel sides.
O A. True
OB. False
Answers
Simplify and show your work. \((6i)(-2i)(-6-4i)\)
Answers
Answer:
- 72 - 48i
Step-by-step explanation:
note that i² = - 1
(6i)(- 2i)(- 6 - 4i)
= - 12i²(- 6 - 4i)
= - 12(- 1)(- 6 - 4i)
= 12(- 6 - 4i) ← distribute parenthesis by 12
= - 72 - 48i
Simplify the expression by first substituting values from the table of exact values and then simplifying the resulting expression. Answer exactly. 4 sin 30 ∘ =
Answers
The expression is simplified to 2
How to determine the valueIt is important to note that the table of exact values for trigonometric identity differ with the particular identity in study.
From the table of exact values, we have that;
sin 15 = 0. 25
sin 30 = 0. 5000
sin 45 = 0. 7071
sin 60 = 0. 8600
sin 75 = 0. 9659
sin 90 = 1
To determine the value of the expression, we have to substitute the value of sin 30 as 0. 5000
4 sin 30°
⇒ 4 × 0. 5000
multiply through
⇒ 2
The value determined is 2
Thus, the expression is simplified to 2
Learn more about trigonometric identity here:
https://brainly.com/question/7331447
#arSPJ1
how to divide −6x2−3x+12 by 3x−3.
Answers
solve -6x2-3x+12 dived by 3x-3 using pemdas
Step-by-step explanation:
The question is how to divide this this is how to solve it
write an expression to show how much longer the round trip to Las Vegas id than the round trip to cheyenne... Cheyenne round trip is 202 and Las Vegas round trip is 1498
Answers
Answer:
GPS is access
Step-by-step explanation:
Plz hurry!!! The scale on a map shows that 2 inches represents 15 miles. Which proportion can be used to find the actual
distance, x, represented by 30 inches on the map?
2 30
O 15
х
O
2.
15
30 x
Answers
Answer: 50
Step-by-step explanation:
A specimen of 100 mm length along the stroke of a shaper is machined with 15° rake angle tool. Determine the shear plane angle and chip thickness if uncut chip thickness is 1.5 mm and chip length obtained is 40 mm.
Answers
The shear plane angle is approximately 84.3°, and the chip thickness is approximately 15.1 mm.
What is the shear plane angle?To determine the shear plane angle and chip thickness in the given scenario, we can use the following formulas:
Shear Plane Angle (α):
tan(α) = tan(β - φ)
where β is the inclination angle of the machined surface (rake angle) and φ is the friction angle.
Chip Thickness (t):
t = tc / cos(α)
where tc is the uncut chip thickness.
Given:
Uncut chip thickness (tc) = 1.5 mm
Chip length (lc) = 40 mm
Length of the specimen (L) = 100 mm
Rake angle (β) = 15°
First, we need to calculate the shear plane angle (α):
tan(α) = tan(β - φ)
Since the friction angle (φ) is not given, we will assume a typical value of 5°.
tan(α) = tan(15° - 5°)
tan(α) = tan(10°)
α ≈ 84.3° (rounded to two decimal places)
Next, we can calculate the chip thickness (t):
t = tc / cos(α)
t = 1.5 mm / cos(84.3°)
t ≈ 15.1 mm (rounded to two decimal places)
Learn more on shear plane angle here;
https://brainly.com/question/14881618
#SPJ1
For a géometric sequence, if a1=9 and a5
=2304, what is the value of r?
Answers
The value of common ration r is 4.
Given that,
a₁ = 9
a₅ = 2304
We know that,
A geometric sequence is a sequence in which each term (except from the first term) is multiplied by a fixed amount to obtain the following term.
The following term in the geometric sequence must be obtained by multiplying it by a set term (referred to as the common ratio), and the previous term in the sequence can be obtained by dividing it by the same common ratio.
Since we know that nth term of GP is,
\(a_{n}\) = a₁ \(r^{n-1}\)
Therefore,
a₅ = a₁ \(r^{4}\) = 2304
⇒ 9 x \(r^{4}\) = 2304
⇒ \(r^{4}\) = 256
⇒ r = 4
Hence, r = 4
To learn more about GP visit:
https://brainly.com/question/29323941
#SPJ1
the first part of the problem asks them to calculate the work done on the gas when the gas goes from the initial state to the final state shown. here is part of their dialogue: nora: the gas is compressed because the volume decreases. that means that there is work done on the gas, and the work is positive. bob: ok. that's right because we're using the first law with q w. we need to use that area thing to find the work. nora: yeah. we want the area under the line between the dots. bob: that line shows the process, right? nora: yup, that's the one. so the area is one-half times base times height. it's the area of that triangle. bob: but you have to add the area of that skinny rectangle below it, don't you? nora: i don't think so. that bottom dot for the final state tells you where the bottom of the area is. bob: why don't we ever agree? tell you what. we'll each try our own way and let webassign tell us who's right. nora: hmmm... i hope i get the big, green check mark!
Answers
To determine how much effort the gas undergoes as it changes from its original condition to its final one, Nora and Bob utilize the area underneath the line separating the two states and the first rule of thermodynamics.
When a gas changes from its initial condition to its final state, Nora and Bob explain how to compute the work that is done. They talk about compressing gas, thus something is being done to the gas.
You suggest using the area under the line separating the final and initial states to calculate the work done as well as the application of the first equation of thermodynamics, q=w.
To learn more about the work done at
https://brainly.com/question/13662169?referrer=searchResults
#SPJ4
Al uses a box in the shape of a rectangular prism as shown in the diagram to for his coin collection.
What is the volume of this box?
192in³
275in³
37512 in³
425in³
Answers
Answer:
4 x 8.5 x 12.5 =425 (multiple hight x width x length)
The volume of the box is \(425in^{3}\)
Please help I’m stuck

Answers
Answer: any negative value
Step-by-step explanation:
g(x)= ax², inc on x<0 & dec on x>0
Firstly we need to get the derivative of g(x)
g'(x)=2ax
for inc interval g'(x) should be +ve
x<0 (i.e. x= -ve), then a must be -ve
for dec interval g'(x) should be +ve
x>0 (i.e. x= +ve), then a must be -ve
so in both cases a must be a negative constant
Crane Corporation is considering purchasing a new delivery truck. The new truck would cost $55,440. The new truck is expected to generate a cost savings of $7,700. At the end of 8 years, the company will sell the truck for an estimated $27,600.
Traditionally the company has used a rule of thumb that a proposal should not be accepted unless it has a payback period that is less than 50% of the asset's estimated useful life. Larry Newton, a new manager, has suggested that the company should not rely solely on the payback approach, but should also employ the net present value method when evaluating new projects. The company's cost of capital is 8%.
a) Compute the cash payback period and net present value of the proposed investment.
b) Does the project meet the company's cash payback criteria?
c) Does it meet the net present value criteria for acceptance?
Answers
A. The payback period is 7.2 years. The net present value of the proposed investment is 3720.55.
B. No, the project does not meet the company's cash payback criteria.
C. Yes, the project does meet the net present value criteria for acceptance.
How do we solve for the net present value of the proposed investment?A. The truck costs $55,440 and generates annual cost savings of $7,700. So the payback period is the cost of the truck divided the expected amount the truck will generate.
$55,440 / $7,700 = 7.2 years
To solve for the net present value, we say
Net Present Value = ∑ [(Cash inflow in period t) / (1 + \(r^{t}\)] - Initial Investment.
NPV = (($7,700 / (1 + 0.08)¹) = 7 129.63
+ ($7,700 / (1 + 0.08)²) = 6601.51
+ .($7,700 / (1 + 0.08)³ = 6112.51
+ ($7,700 / (1 + 0.08)⁴) = 5659.73
+ ($7,700 / (1 + 0.08)⁵) = 5240.49
+ ($7,700 / (1 + 0.08)⁶) = 4 852.31
+ ($7,700 / (1 + 0.08)⁷) = 4492.88
+($7,700 / (1 + 0.08)⁸) = 4160.07
+ ($27,600 / (1 + 0.08)⁸)) = 14911.42
- $55,440
We add all these values together and subtract by $55,440
7 129.63 + 6601.51 + 6112.51 + 5659.73 + 5240.49 +4 852.31 + 4492.88 + 4160.07 + 14911.42 - $55,440
59160.55 - 55,440
NPV = 3720.55
B. The cash payback period of the project is 7.2 years. The company's cash payback criteria state that a project should not be accepted unless it has a payback period that is less than 50% of the asset's estimated useful life, which would be 4 years which is 50% of 8 years. Since 7.2 years is greater than 4 years, the project does not meet the company's cash payback criteria.
C. The positive NPV of $3,720.55 shows that embarking on the prooject will be valuable to the company. This means the project meets the NPV criteria for acceptance.
Find more exercises on net present value;
https://brainly.com/question/27557482
#SPJ1
A baseball pitcher has made 53 pitches in the first four innings of a baseball game and plans to pitch 3 mote innings. The manager of the team has committed to allowing his pitcher to throw, at most, pitches during the game. Write an inequality to find the average number of pitches the pitcher can throw over the next three innings Solve the inequality from Part 1. What is the maximum number of pitches the pitcher can make in cach of the next 3 innings ? Graph your solution from Part 2 on a number line and explain what your solution means. If the pitcher threw just 6 pitches in the fifth inning, what is the greatest number of pitches the pitcher can throw per inning he wishes to pitch nine innings? Write and solve an inequality to answer this part.
Answers
Answer:
at most 17 pitches per inning
Step-by-step explanation:
It is given that a baseball pitcher makes 53 pitches in the first 4 innings of a game and plans to pitch in the next 3 innings.
We need to write and solve an inequality to find the possible average pitches per inning the pitcher made in the next 3 innings if the pitcher is assigned a maximum of 105 pitches.
From part (a) we know 3 p + 53 3p+53 represents the total number of pitches made if the pitcher makes an average of p pitches per inning in the next 3 innings.
If the pitcher can make at most 105 pitches, then:
3 p + 53 ≤ 105 3p+53≤105
To solve the inequality, first subtract 53 on both sides of the inequality to isolate the variable term:
3 p + 53 − 53 ≤ 105 − 53 3 p ≤ 53
3p+53≤105 \(p\leq 17\frac{1}{3}\)
at most 17 pitches per inning
(Hope this helps can I pls have brainlist (crown)☺️)
Which point has the coordinates (3,-2)
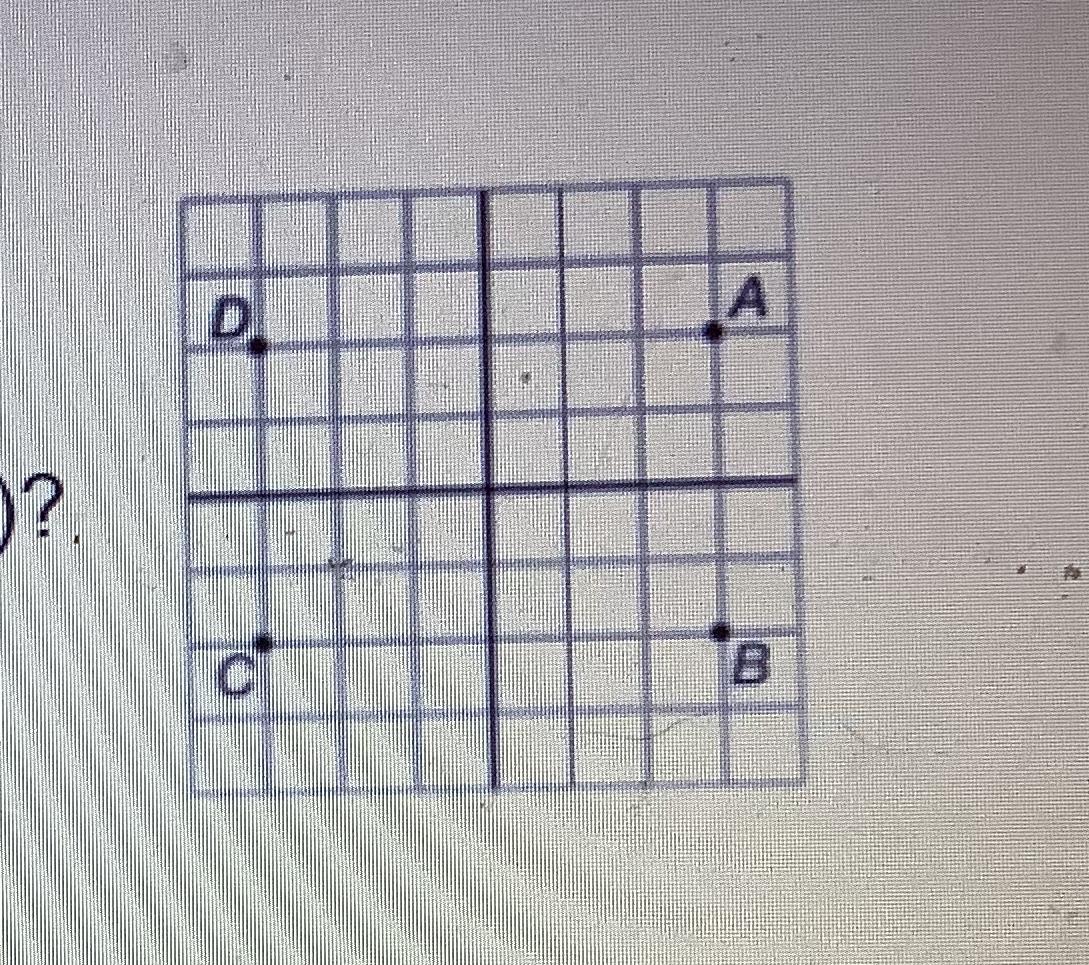
Answers
Answer:
B
Step-by-step explanation:
Since x is 3, you go 3 units right. Since y is -2, you go 2 units down.
Tom bought a painting for £180 He sold the painting for £300 Work out the precentage profit give your answer in a Whole number
Answers
Answer:
To calculate the percentage profit on the sale of the painting, we need to first find the difference between the selling price and the cost price. In this case, the selling price is £300 and the cost price is £180, so the difference is £300 - £180 = £120.
We can then divide this difference by the cost price and multiply by 100% to express the profit as a percentage. In this case, the profit is £120 / £180 * 100% = 66.67%.
Since we need to express the profit as a whole number, we can round this value to the nearest whole number, which gives us a profit of 67%. Therefore, Tom made a profit of 67% on the sale of the painting.