What method can you use to find the area of the composite figure? Select three options.
A large rectangle. A smaller rectangle is connected on the right side.
Decompose the figure into two rectangles and add the areas.
Decompose the figure into three rectangles and add the areas.
Extend the top and rightmost sides to make a larger rectangle, find its area, and then subtract the area of the removed corner.
Decompose the figure into two rectangles, find their sum, and then add the area of the removed corner.
Decompose the figure into two rectangles, find their sum, and then subtract the area of the removed corner.
Answers
Answer:
a)Decompose the figure into two rectangles and add the areas.
Step-by-step explanation:
i did the unit test and got a 100 and also the two areas would added together would equal the area through the entire figure hopes this helps;)
Answer:
A. B. C. Are all the correct shapes.
Step-by-step explanation:
Related Questions
help please i rlly don’t understand math

Answers
2.-2x slope -3 y intercept
H=(...-2,-10,1,2,...3what type of set is H
A : empty set
B: finite set
C: infinity set
D: universal set
Answers
Answer: Universal set
Step-by-step explanation:
A universal set is usually represented by U and it is set that has all the elements of a related sets.
For example, if there are two sets which are X and Y. Let's say X = {1,2,3} and Y = {1,a,b,c}, therefore, the universal set will be U = {1,2,3,a,b,c}.
In the above scenario, H(...-2,-10,1,2,...3) is a Universal set.
Which answer choice correctly represents the quotient of 28,134 divided by 71?
A.
B.
C.
D.
Answers
Answer:
please give brainliest
Step-by-step explanation:
396.253521127
Calculate the value of the unknown angle

Answers
Answer:
80+2x=180°{co-interior angle}
2x=180-80
2x=100
x=50°
hope it helps.
Angle D = 80
Angle A+B+C+D = 360
Angle C = Angle A
Angle A = 2x
80+80+2x+2x = 360
160+4x=360
4x=360-160
4x=200
X=200/4
x=50
louis created a square garden with a side length of 5 feet. what is the total area of the garden
Answers
Answer:
the answer of the question is 25
Solve the following equation for all radian solutions and if 0 ≤ t < 2π. Give all answers as exact values in radians. Do not use a calculator. (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
1. 9 cos t -root3=7cost
a) all radian solutions (Let k be any integer.) t= ______rad
b) 0 ≤ t < 2π. t= ______rad
2.3 cos t = 9 cos t − 3 root3
a) all radian solutions (Let k be any integer.) t= ______rad
b) 0 ≤ t < 2π. t= ______rad
3.5 sin t + 8 = −3 sin t
a) all radian solutions (Let k be any integer.) t= ______rad
b) 0 ≤ t < 2π. t= ______rad
Answers
In this problem set, we will be solving three different equations involving trigonometric functions. Within the interval 0 ≤ t < 2π, the solutions are t = π/6 and t = 11π/6. Within the interval 0 ≤ t < 2π, the solutions are t = π/3 and t = 5π/3. And for the third equation, there is no solution.
When solving these equations, we will be looking for all radian solutions, as well as solutions within the interval 0 ≤ t < 2π.
It's important to remember that an equation is simply a mathematical statement that shows that two expressions are equal. In order to solve the equation, we need to manipulate the expressions in such a way that we can isolate the variable we are solving for.
For the first equation, we are given 9 cos t - root3 = 7 cos t. To solve for t, we want to isolate the cosine term on one side of the equation. We can do this by subtracting 7 cos t from both sides, which gives us 2 cos t - root3 = 0. Next, we can divide both sides by 2 to get cos t = root3/2. We recognize that this is a special angle for cosine, which occurs at π/6 and 11π/6 radians. Therefore, the solutions for all radian values of t are t = π/6 + 2kπ and t = 11π/6 + 2kπ, where k is any integer. Within the interval 0 ≤ t < 2π, the solutions are t = π/6 and t = 11π/6.
For the second equation, we have 3 cos t = 9 cos t - 3 root3. Similar to the first equation, we want to isolate the cosine term on one side, so we can subtract 9 cos t from both sides, which gives us -6 cos t = -3 root3. Dividing both sides by -6, we get cos t = 1/2 root3. Again, this is a special angle for cosine, which occurs at π/3 and 5π/3 radians. Therefore, the solutions for all radian values of t are t = π/3 + 2kπ and t = 5π/3 + 2kπ, where k is any integer. Within the interval 0 ≤ t < 2π, the solutions are t = π/3 and t = 5π/3.
For the third equation, we have 5 sin t + 8 = -3 sin t. To isolate the sine term, we can add 3 sin t to both sides, which gives us 8 = -2 sin t. Dividing both sides by -2, we get sin t = -4. This is not a valid solution, as the range of the sine function is between -1 and 1. Therefore, there is no solution to this equation.
For more such questions on Solutions.
https://brainly.com/question/29016480#
#SPJ11
What is the key underlying assumption of the single index
model?
Answers
The key underlying assumption of the single index model is that the return of a security can be explained by the return of a broad market index.
This assumption forms the basis of the single index model, also known as the market model or the capital asset pricing model (CAPM).
In this model, the return of a security is expressed as a function of the return of the market index. The single index model assumes that the relationship between the returns of a security and the market index is linear.
It suggests that the risk and return of a security can be explained by its exposure to systematic risk, which is represented by the market index.
The single index model assumes that the return of a security can be decomposed into two components: systematic risk and idiosyncratic risk.
Systematic risk refers to the risk that cannot be diversified away, as it affects the entire market. Idiosyncratic risk, on the other hand, is the risk that is specific to a particular security and can be diversified away by holding a well-diversified portfolio.
The single index model assumes that the systematic risk is the only risk that investors should be compensated for, as idiosyncratic risk can be eliminated through diversification.
It suggests that the expected return of a security is determined by its beta, which measures its sensitivity to the market index. A security with a higher beta is expected to have a higher return, as it is more sensitive to market movements.
To know more about capital asset pricing model click on below link:
https://brainly.com/question/33539143#
#SPJ11
This shape has been made from two identical isosceles triangles.
250
х
Work out the size of angle x.

Answers
Answer:
100°Step-by-step explanation:
Half of angle x is the exterior angle of the triangles with both non-adjacent angles of 25° (same angles opposite same sides)
x/2 = 2*25°x = 2*50° x = 100°Step-by-step explanation:
x/2 = 2*25°
x = 2*50°
x = 100°
answer 100
The dean of Blotchville University boasts that the average class size there is 20. But the reality experienced by the majority of students there is quite different: they find themselves in huge courses, held in huge lecture halls, with hardly enough seats or Haribo gummi bears for everyone. The purpose of this problem is to shed light on the situation. For simplicity, suppose that every student at Blotchville University takes only one course per semester.
a) Suppose that there are 16 seminar courses, which have 10 students each, and 2 large lecture courses, which have 100 students each. Find the dean’s eye view average class size (the simple average of the class sizes) and the student’s eye view average class size (the average class size experienced by students, as it would be reflected by surveying students and asking them how big their classes are). Explain the discrepancy intuitively.
b) Give a short proof that for any set of class sizes (not just those given above), the dean’s eye view average class size will be strictly less than the student’s eye view average class size, unless all classes have exactly the same size.
Answers
a) Find the dean’s eye view average class size and the student’s eye view average class size:Given that there are 16 seminar courses, each having 10 students each.Number of students in seminar courses: 16 × 10 = 160There are 2 large lecture courses, each having 100 students each.
Number of students in large lecture courses: 2 × 100 = 200
Dean’s view average class size is the simple average of the class sizes:Let’s find the Dean’s view average class size. There are 18 courses in total.
This can be obtained by dividing the total number of students by the total number of classes.
Student’s view average class size = Total number of students/Total number of classes
= 360/18
= 20
Therefore, the dean’s eye view average class size is 46.67 (approximately) and the student’s eye view average class size is 20.
Now, we need to prove that D 2, then (k/(k + 1)) - (1/n) < 0.
Therefore, we have:
S - D< (c2 - c1)*[(k/(k + 1)) - (1/n)]< 0
Hence, S < D.Therefore, the dean’s eye view average class size will be strictly less than the student’s eye view average class size, unless all classes have exactly the same size.
To know more about size visit:
https://brainly.com/question/32316671
#SPJ11
Please help will give brainlest hurry
Find the product of (3x − 2)(x + 3).
3x2 − 7x − 6
3x2 + 7x − 6
3x2 − 7x − 1
3x2 + 7x − 1
Answers
Answer:
\(\huge\boxed{\sf 3x\² + 7x - 6}\)
Step-by-step explanation:
Given expression:= (3x - 2)(x + 3)
Distribute= 3x(x + 3) - 2(x + 3)
Again, distribute= 3x² + 9x - 2x - 6
Combine like terms= 3x² + 7x - 6\(\rule[225]{225}{2}\)
3x•3 = 9x
-2•x = -2x
-2•3 = -6
9x-2x = 7x
3x^2 + 7x - 6
How do i find a constant proportionality if there is no proporstional relationship? - 7th Grade Math Help.
Answers
Answer:To check if the 2 quantities are proportional or not, we have to find the ratio of the two quantities for all the given values. If their ratios are equal, then they exhibit a proportional relationship. If all the ratios are not equal, then the relation between them is not proportional.
Step-by-step explanation:
Hope this helps!
Consider the initial value problem y' = y 2 cos x,y F 1. a. c. Estimate y() using Euler's Method with 3 steps. Include the complete table. Use the same headings we used in class.
Answers
To estimate the value of y at x=1 using Euler's method with 3 steps, we can apply the iterative process. Therefore, using Euler's method with 3 steps, we estimate that y(1) is approximately 1.353.
To use Euler's method, we start with an initial condition and take small steps to approximate the solution of the differential equation. In this case, the initial condition is y(0) = 1. We will take three steps with a step size of h = 0.1.
Using Euler's method, we can calculate the approximations of y at each step using the formula y(i+1) = y(i) + h * f(x(i), y(i)), where f(x, y) is the given differential equation.
Here is the table showing the calculations:
Step | x | y | f(x, y) | y(i+1)
1 | 0 | 1 | 1 | 1 + 0.1 * 1 = 1.1
2 | 0.1 | 1.1 | 1.2109 | 1.1 + 0.1 * 1.2109 = 1.2211
3 | 0.2 | 1.2211| 1.3286 | 1.2211 + 0.1 * 1.3286 = 1.353
Therefore, using Euler's method with 3 steps, we estimate that y(1) is approximately 1.353.
Learn more about Euler's method here:
https://brainly.com/question/30699690
#SPJ11
Find the value of x and y.

Answers
Answer:
C
Step-by-step explanation:
I did the same exam.
(jk)
Answer:
what are you supposed to solve for x and y
Step-by-step explanation:
what are the coordinates of B if the midpoint of line segment AB is (2, -5) and the coordinates of point A is (4, 4)?
Answers
What are the answers for 1 through 4?? if you know you'll get brainliest.

Answers
Answer:
Give me the brainlest, please?
Step-by-step explanation:

If you have 140. mL of a 0.100M PIPES buffer at pH6.80 and you add 4.00 mL of 1.00MHCl, what will be the new pH? (The p K_a of PIPES is 6.80.) pH=
Answers
The new pH after adding 4.00 mL of 1.00 M HCl to 140 mL of a 0.100 M PIPES buffer at pH 6.80 is still pH 6.80.
To determine the new pH of the solution after adding the HCl, we need to calculate the resulting concentration of the PIPES buffer and use the Henderson-Hasselbalch equation.
Given:
Initial volume of PIPES buffer (V1) = 140 mL
Initial concentration of PIPES buffer (C1) = 0.100 M
Initial pH (pH1) = 6.80
Volume of HCl added (V2) = 4.00 mL
Concentration of HCl (C2) = 1.00 M
pKa of PIPES = 6.80
Step 1: Calculate the moles of PIPES and moles of HCl before the addition:
Moles of PIPES = C1 * V1
Moles of HCl = C2 * V2
Step 2: Calculate the moles of PIPES and moles of HCl after the addition:
Moles of PIPES after addition = Moles of PIPES before addition
Moles of HCl after addition = Moles of HCl before addition
Step 3: Calculate the total volume after the addition:
Total volume (Vt) = V1 + V2
Step 4: Calculate the new concentration of the PIPES buffer:
Ct = Moles of PIPES after addition / Vt
Step 5: Calculate the new pH using the Henderson-Hasselbalch equation:
pH2 = pKa + log10([A-] / [HA])
[A-] is the concentration of the conjugate base (PIPES-) after addition (Ct)
[HA] is the concentration of the acid (PIPES) after addition (Ct)
Let's calculate the values:
Step 1:
Moles of PIPES = 0.100 M * 140 mL = 14.0 mmol
Moles of HCl = 1.00 M * 4.00 mL = 4.00 mmol
Step 2:
Moles of PIPES after addition = 14.0 mmol
Moles of HCl after addition = 4.00 mmol
Step 3:
Total volume (Vt) = 140 mL + 4.00 mL = 144 mL = 0.144 L
Step 4:
Ct = 14.0 mmol / 0.144 L = 97.22 mM
Step 5:
pH2 = 6.80 + log10([97.22 mM] / [97.22 mM]) = 6.80.
Learn more about Henderson-Hasselbalch equation from the given link!
https://brainly.com/question/16963838
#SPJ11
Which algebraic expressions are polynomials? Check all that apply.
0
mx - √3+5y
0x²y2-4x³+12y
04-x²
√x-16
3.9x³-4.1x² + 7.3
Answers
the options that are polynomials are:
3.9x³-4.1x² + 7.3
x²y²-4x³+12y
4-x²
Which algebraic expressions are polynomials?A polynomial is an expression of the form:
p(x) = aₙ*xⁿ + ...+ a₂*x² + a₁*x + a₀
Where all the exponents of the variable are whole numbers, and in this case we have only one variable x, but we could have any number of variables.
With that in mind, the options that are polynomials are:
3.9x³-4.1x² + 7.3
x²y²-4x³+12y
4-x²
These 3 expressions are polynomials.
If you want to learn more about polynomials:
https://brainly.com/question/4142886
#SPJ1
(-20, 12)
(17, 2)
(-11, 8)
(17, 8)
(11, 2)
Is this relation a function?
Answers
Answer:
No because x-coordinate 17 appears twice.
Step-by-step explanation:
In a function, no two ordered pairs can have the same x-coordinate.
Here, points (17, 2) and (17, 8) have 17 as the x-coordinate. Since the same x-coordinate, 17, is used more than once, this relation is not a function.
what is the correct measure of m? 15, 5, n, m
Answers
Answer:
subtract 5 , m=(-15)
Step-by-step explanation:
15-5
=10
n:
5-10
=(-5)
m:
(-5)-10
=(-15)
hope it help
solve for x and y
7x+12
12x-28
9y-77
Answers
Answer: x= 9y - 77 its vertical intercep 0, -77
Still struggling with this.

Answers
Answer:
22
Step-by-step explanation:
You add up the value of each X and you get a final answer of 22. Have a great day!
What is the distance between the following points?

Answers
Answer:
\(\sqrt{85}\) or 9.21954
Step-by-step explanation:
Use the distance formula to determine the distance between the two points.
\(d = \sqrt{(x_{2} -x_{1})^{2} + (y_{2} - x_{1})^{2} }\)
d = distance
\((x_{1}, y_{1})\) = coordinates of the first point
\((x_{2}, y_{2})\) = coordinates of the second point
{I need help- please T^T}
Question: Which of the following expressions are equivalent to..
(I can't type it but ill put a picture of it)

Answers
Answer:
Khan Academy! B
Step-by-step explanation:
-(-b)/a can be written as (-(-a))/b
double negatives give a positive: a/b
and we can similarly manipulate option B to get a/b (a/(-(-b))) is a/b
thus the expression is equivalent to option B
What is the mass of one
box of nails?
Answers
Answer:
nails weight 50 lbs by knowing the weight u can find the mss
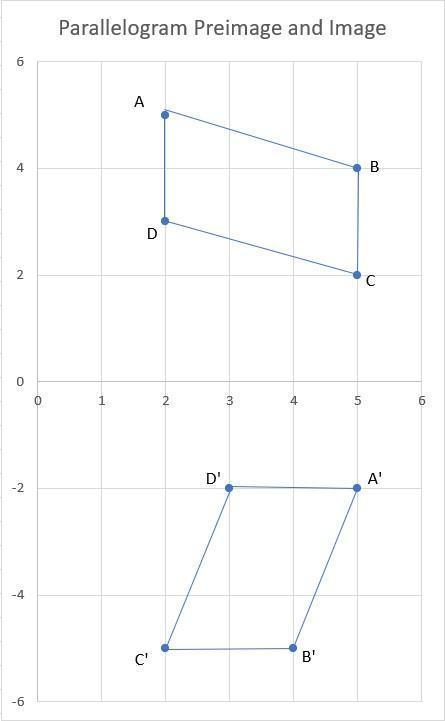
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Please I want sleep I need sleep

Answers
Answer:
1 1/3
Step-by-step explanation:
2/5 x 10/3
Multiply across -
10 x 2 = 20
5 x 3 = 15
20/15
Simplify -
20/15 to 4/3
Divide 4 by 3
You get 1 1/3
Answer:
4/3
Step-by-step explanation:
multiply (top) numerator x numerator and (bottom) denominator x denominator2 x 10 = 20 and 5 x 3 = 15 or 20/15 So, 2/5 x 10/3 = 20/15reduce 20/15 to simplest terms, both are divisible by 5divide both numerator and denominator by 5 and get:20/15 = 4/3So, 2/5 x 10/3 = 4/3
explain how a box plot can be used to determine whether a distribution of values is essentially symmetric.
Answers
It allows us to quickly identify whether a distribution is symmetric or skewed, and to spot outliers or other unusual features in the data.
A box plot is a graphical representation of a set of data that displays the distribution of values. It consists of a box that spans the interquartile range (IQR) and a line inside the box that represents the median value. The whiskers extend from the box to the minimum and maximum values within 1.5 times the IQR. Outliers are plotted as individual points outside the whiskers.
To determine whether a distribution of values is essentially symmetric, we can look at the box plot. If the median line is at the center of the box, and the whiskers are of equal length on either side, the distribution is approximately symmetric. However, if the box is shifted to one side, or the whiskers are of different lengths, the distribution is skewed.
In addition to the box plot, we can also look at other measures of central tendency and dispersion, such as the mean and standard deviation. If the mean and median are close to each other, and the standard deviation is not too large, the distribution is likely to be symmetric.
Overall, a box plot is a useful tool for visualizing and analyzing distributions of values.
It allows us to quickly identify whether a distribution is symmetric or skewed, and to spot outliers or other unusual features in the data.
To know more about symmetric refer here
https://brainly.com/question/14466363#
#SPJ11
Given the function f(x)=2x²+3, what is the average rate of change of f on the interval [2,2+h]?
Answers
Answer:
5.2
Step-by-step explanation:
help click all the questions



Answers
Answer:1,grams 2,b 3, id k srry
Step-by-step explanation:
9. B
10. B
(i think..)
write an equation of the parabola in vertex form calculator
Answers
A parabola's vertex form equation is as follows:
y = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola.
To use a calculator to find the equation of a parabola in vertex form, you would typically need to know the coordinates of the vertex and at least one other point on the parabola.
Determine the vertex coordinates (h, k) of the parabola.
Identify at least one other point on the parabola (x, y).
Substitute the values of the vertex and the additional point into the equation y = a(x - h)^2 + k.
Solve the resulting equation for the value of 'a'.
Once you have the value of 'a', substitute it back into the equation to obtain the final equation of the parabola in vertex form.
Note: If you provide specific values for the vertex and an additional point, I can assist you in calculating the equation of the parabola in vertex form.
To know more about Parabola, visit
brainly.com/question/29635857
#SPJ11