what proportion of the children of this couple will have neither condition? what proportion of the children of this couple will have neither condition? 12/16 9/16 7/16 6/16 4/16 3/16 1/16
Answers
The proportion of children who will be carriers of one or both conditions (Aa genotype) is 2/4 or 1/2. The closest answer is 1/2 or 8/16.
To determine the proportion of children who will be carriers of one or both conditions, we can use the principles of Mendelian genetics.
Given that both conditions (CF and PKU) are autosomal recessive and assort independently, we can calculate the probabilities of different genotypes in the children.
Let's represent the dominant allele for each condition as "A" and the recessive allele as "a".
For a heterozygous individual (Aa), there are three possible genotypes:
1. AA - Homozygous dominant
2. Aa - Heterozygous carrier
3. aa - Homozygous recessive (affected individual)
Since both parents are heterozygous for both conditions (Aa), the Punnett square for their offspring would be as follows:
CF CF
-------------------
PKU | AA Aa
PKU | Aa aa
Looking at the Punnett square, we can determine the proportions of different genotypes in the offspring:
1. The probability of having an AA genotype (homozygous dominant) for both conditions is 1/4.
2. The probability of having an Aa genotype (heterozygous carrier) for at least one condition is 2/4 (or 1/2).
3. The probability of having an aa genotype (homozygous recessive) for at least one condition is 1/4.
Therefore, the proportion of children who will be carriers of one or both conditions (Aa genotype) is 2/4 or 1/2.
In terms of the given options, the closest answer is 1/2 or 8/16.
Learn more about Punnett square here:
https://brainly.com/question/32049536
#SPJ11
A male and a female are each heterozygous for both cystic fibrosis (CF) and phenylketonuria (PKU). Both conditions are autosomal recessive, and they assort independently.
What proportion of the children will be carriers of one or both conditions?
12/16
9/16
8/16
7/16
6/16
4/16
3/16
1/16
Related Questions
(1 point) college officials want to estimate the percentage of students who carry a gun, knife, or other such weapon. how many randomly selected student
Answers
Probability Theory
P (K) =\(\frac{n (K) }{n (S)}\)
P(K) : probability of selected K
n (K) : number of occurence of K
n (S) : number of all occurence
In question is not contain information about the number of students who curry a gun, knife, or other weapon and the number of all students. so, we can desribe that :
n (A) : the number of occurence of students who curry a gun
n (B) : the number of occurence of students who curry a knife
n (C) : the number of occurence of students who curry other weapon
and the number of all students is n ( A U B U C) -> union of sets
how many randomly selected student? in question, there is no specific about the student. so, we can answer with :
1) probability of students who curry a gun
P (A) = \(\frac{n (A) }{n (AUBUC)}\)
2) probability of students who curry a knife
P (B) = \(\frac{n (B) }{n (AUBUC)}\)
3) probability of students who curry other weapon
P (C) = \(\frac{n (C) }{n (AUBUC)}\)
and if question want to estimate with percentage, we can multiply with 100%. example :
1) percentage of probability of students who curry a gun
P (A) = \(\frac{n (A) }{n (AUBUC)}\) x 100%
read more about probability at https://brainly.com/question/9772981
#SPJ4
In each graphic, the triangle was dilated to create the image triangle. Determine which scale factor was used for each dilation by dragging the correct scale factor to each graph.
pls help i well give brllant

Answers
The scale factor was used for each dilation are-
Part a: For ΔABC - scale factor = 2Part b: For ΔDEF - scale factor = 1/2Part c: For ΔGHJ - scale factor = 1/3Part d: For ΔKML - scale factor = 3Explain about the dilation:A transformation that changes the size of a figure is called a dilatation. This indicates that the preimage as well as image are similar and have been scaled up or down, respectively.
A dilatation that results in a reduction (imagine shrinking) or an enlargement (think stretching) produces a smaller or larger image, respectively.
Part a: For ΔABC
Length AB = 2 units
Length A'B' = 4 units
A'B' = 2 *AB
Thus, For ΔABC - scale factor = 2
Part b: For ΔDEF -
Length DF = 2 units
Length D'F' = 1 units
D'F' = 1/2 DF
Thus, For ΔDEF - scale factor = 1/2
Part c: For ΔGHJ -
Length GH = 3 units
Length G'H' = 1 units
G'H' = 1/3 GH
Thus, For ΔGHJ - scale factor = 1/3
Part d: For ΔKML -
Length KM = 2 units
Length K'M' = 6 units
K'M' = 3*KM
Thus, For ΔKML - scale factor = 3
Know more about the dilation
https://brainly.com/question/3457976
#SPJ1
Please solve correctly

Answers
Answer:
f(-3) =8
Step-by-step explanation:
Answer:
Step-by-step explanation:
Answer
f(x) has the same meaning as y. So you could rewrite the question as "What value of x gives y a value of 8"
The graph tells you that x = - 3 when y = 8.
f(-3) = 8
The energy eigenfunctions psi_1, psi_2, psi_3, and psi_4 corresponding to the four lowest energy states for a particle confined in the finite potential well V(x) = -V_0 |x| < a/2 0 |x| > a/2 are sketched in Fig. 4.4. For which of these energy eigenfunctions would the probability of finding the particle outside the well, that is, in the region |x| > a/2, be greatest? Explain. Justify your reasoning using the solution to the equation in the region x > a/2.
Answers
In summary, the energy eigenfunction psi_4 has the greatest probability of finding the particle outside the well because it has the largest amplitude in the region |x| > a/2, as evidenced by the fact that it has a node at x=a/2.
To determine which energy eigenfunction has the greatest probability of finding the particle outside the well, we need to examine the wave function in the region |x| > a/2. Since the potential outside the well is zero, the wave function in this region can be expressed as a linear combination of the energy eigenfunctions:
ψ(x) = A1ψ1(x) + A2ψ2(x) + A3ψ3(x) + A4ψ4(x)
where A1, A2, A3, and A4 are constants determined by the boundary conditions.
To find the probability of finding the particle outside the well, we need to calculate the integral of the square of the wavefunction over the region |x| > a/2:
P = ∫(|ψ(x)|^2)dx, where the integral is taken over the region |x| > a/2.
Since we want to find the energy eigenfunction with the greatest probability of finding the particle outside the well, we need to maximize this probability, which means we need to find the energy eigenfunction with the largest amplitude in the region |x| > a/2.
From Fig. 4.4, we can see that the energy eigenfunction with the largest amplitude in the region |x| > a/2 is psi_4. Therefore, the energy eigenfunction psi_4 has the greatest probability of finding the particle outside the well. This is because psi_4 has a node at x=a/2, which means that the wavefunction is zero at this point and the particle has a higher probability of being found outside the well.
In summary, the energy eigenfunction psi_4 has the greatest probability of finding the particle outside the well because it has the largest amplitude in the region |x| > a/2, as evidenced by the fact that it has a node at x=a/2.
Learn more about amplitude here:
https://brainly.com/question/8662436
#SPJ11
What is 17x5.8 show your work

Answers
Answer: 98.6
Step-by-step explanation:
5.8 can be broken down into 5 & 0.8
17 timed 5 = 85
17 timed 0.8 = 13.6
85+13.6 = 98.6
PLEASE ANSWER ASAP AND DONT BE A SPAM What is the scale factor of the following similar polygons?
scale factor =

Answers
Answer:
Step-by-step explanation:
The scale factor is 35/42 = 5/6
The total number of pennies on Row 1 is: 1 2 4 8 16 32 64 128 =.
Answers
The pennies placed on the squares D, E, F, G, and H will be 8, 16, 32, 64, and 128 pennies.
Given
There are 8 rows and 8 columns, which means 64 squares on a chessboard.
We are placing 1 penny on Row 1 Column A, 2 pennies on Row 1 Column B, 4 pennies on Row 1 Column C, and so on.
What is the matrix?A matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
So, we are increasing the number of pennies twice the amount of the previous square.
So, the pennies on next squares will be,
\(\rm Column \ D = 2\times 4=8\\\\Column \ E = 2\times 9=16\\\\Column \ F= 2\times 16=32\\\\Column \ G= 2\times 32=64\\\\Column \ H = 2\times 64=128\)
Therefore, the pennies placed on the squares D, E, F, G, and H will be 8, 16, 32, 64, and 128 pennies.
For more details about the matrix refer to the link:
https://brainly.com/question/4492099
How do you mirror a function on the y-axis?
Answers
If the original function is y = x^2, the reflected function on the y-axis will be y = -x^2. The graph of y = x^2 is an upward-facing parabola, and the graph of y = -x^2 is a downward-facing parabola that is reflected across the y-axis.
A function can be mirrored on the y-axis by multiplying its dependent variable by -1. This changes the sign of the y-coordinates of the function, which results in a reflection of the graph across the y-axis.
The y-axis is a vertical line that runs through the origin of the coordinate plane, where x=0. A point (x, y) on the original function is reflected on the y-axis to become (-x, -y). The new function will have the same shape as the original function, but with a reflection across the y-axis.
To reflect a function f(x) on the y-axis, we create a new function g(x) as follows:
g(x) = -f(x)
For example, if the original function is y = x^2, the reflected function on the y-axis will be y = -x^2. The graph of y = x^2 is an upward-facing parabola, and the graph of y = -x^2 is a downward-facing parabola that is reflected across the y-axis.
Thus, In conclusion, reflecting a function on the y-axis is a simple transformation that can be achieved by multiplying the dependent variable by -1. This results in a reflection of the graph across the y-axis.
To learn more about parabolas,
Visit; brainly.com/question/29075153
#SPJ4
A group of people were asked if Marilyn Monroe had an affair with JFK. 184 responded "yes", and 387 responded "no". Find the probability that if a person is chosen at random, the person does NOT believes Marilyn Monroe had an affair with JFK.
Probability (round to 4 decimal places)
Answers
Answer:
0.6778 to 4 dec. places.
Step-by-step explanation:
That is 387 / (184+387)
= 387 / 571
= 0.677758
a line segment is a part of a line that is bounded by two distinct end points and contains every point on the line between its endpoints. True/False?
Answers
The statement "a line segment is a part of a line that is bounded by two distinct end points and contains every point on the line between its endpoints." is True because a line segment is defined as a part of a line that is bounded by two distinct end points and contains all the points on the line between those endpoints.
A line segment is a part of a line that has two endpoints and connects them. It is the shortest distance between two points and has a definite length, but no width or height. A line segment can be part of a straight line or a curved line.
A line segment is a section of a line that is defined by two distinct end points and includes every point on the line between them. It is the basic building block of geometry and can be used to measure distances, angles, and shapes.
To learn more about line segment link is here
brainly.com/question/30072605
#SPJ4
Order the numbers from least to greatest -5, 18, 0, -18, 9, -15
Answers
Answer:
below
Step-by-step explanation:
this is very simple one I don't study mathematics but also know this
-18<-15<-5<0<9<18
(Stan itzy)
Find the solution of each of the following systems of linear equations using augmented matrices. a. x - 3y=1 2x - 7y=3 b. x + 2y = 1 3x + 4y =1 c. 2x + 3y = -1 3x + 4y = 2 d. 3x + 4y= 1 4x + Sy= -3
Answers
The solution of each of the following systems of linear equations using augmented matrices are below:
(a) x = -2 and y = -1
(b) x = -1/2 and y = 1
(c) x = -7 and y = 2
(d) Either \(S = \frac{16}{3}\) and there are infinite solutions or\(S \neq \frac{16}{3}\) and there are no solutions
a. x - 3y = 1, 2x - 7y = 3 Putting the above linear equation in augmented matrices form we get:
\(\left[\begin{array}{ccc}1&-3&|1\\2&-7&|3\\\end{array}\right]\)
Performing row operations to solve the above matrix we get:
\(\left[\begin{array}{ccc}1&-3&|1\\0&-1&|1\\\end{array}\right]\) therefore y = -1
and \(\left[\begin{array}{ccc}1&0&|-2\\0&1&|-1\\\end{array}\right]\) therefore x = -2.
b. x + 2y = 1, 3x + 4y = 1 Putting the above linear equation in augmented matrices form we get:\(\left[\begin{array}{ccc}1&2&|1\\3&4&|1\\\end{array}\right]\)
Performing row operations to solve the above matrix we get: \(\left[\begin{array}{ccc}1&2&|1\\0&-2&|-2\\\end{array}\right]\) so y = 1
and \(\left[\begin{array}{ccc}1&0&|\frac{-1}{2} \\0&1&|1\\\end{array}\right]\) so x = \frac{-1}{2}
c. 2x + 3y = -1, 3x + 4y = 2 Putting the above equation in matrix form we get: \(\left[\begin{array}{ccc}2&3&|-1\\3&4&|2\\\end{array}\right]\)
Performing row operations to solve the above matrix we get: \left[\begin{array}{ccc}2&3&|-1\\0&1&|2\\\end{array}\right] therefore y = 2
and \(\left[\begin{array}{ccc}1&0&|-7\\0&1&|2\\\end{array}\right]\) therefore x = -7
d. 3x + 4y = 1, 4x + Sy = -3 Putting the above equation in matrix form we get: \(\left[\begin{array}{ccc}3&4&|1\\4&S&|-3\\\end{array}\right]\)
As the above matrix is not in the echelon form, therefore we perform row operations to convert the matrix into echelon form: \\([\begin{array}{ccc}3&4&|1\\4&S&|-3\\\end{array}\right}]\)
Performing row operation R_{2}→ R_{2}-\frac{4}{3}R_{1}
We get: \(\left[\begin{array}{ccc}3&4&|1\\0&S-\fract{16}{3}&|\frac{-7}{3}\\\end{array}\right]\)
Therefore, either \(S = \frac{16}{3}\) and there are infinite solutions or S ≠ 16/3 and there are no solutions.
To learn more about "Augmented Matrices": brainly.com/question/12994814
#SPJ11
Prove ula kind of proof did you use? Prove that if n is an integer, then n2 + 3n + 2 is an even integer. What method of proof did you use? In this problem, we outline a proof of the following theorem: Theorem 5.6. Let x and y be real numbers. If xy > 1/2, then x2 + yz > 1. "Your mission is to fill in the gaps and blanks, leaving no detail omitted. Proof. The proof will proceed by (insert name of proof technique or description of proof strategy here). So suppose that x- +y < 1. Now we know that (x - y) 2 0. (Insert missing steps of proof here.) Therefore xy < 1/2, and the proof is complete.
Answers
The method of proof used here is a proof by contradiction. We start by assuming that n2 + 3n + 2 is not an even integer, and show that it is not possible for this statement to be true. We then use this to conclude that our original assumption must be false, and thus n2 + 3n + 2 must be an even integer.
To begin, assume that n2 + 3n + 2 is not an even integer. We can represent this statement as "n2 + 3n + 2 = 2k+1, for some integer k." Since the left-hand side of this equation is clearly an even integer, we know that the right-hand side must also be an even integer. This leads to a contradiction, since the right-hand side of the equation is an odd integer.
Therefore, our initial assumption - that n2 + 3n + 2 is not an even integer - must be false. Since the negp-hat is the best estimator of the population mean. true falesation of this statement is true, we have proven that n2 + 3n + 2 must be an even integer.
know more about integer here
https://brainly.com/question/490943#
#SPJ11
Please help!! I’m having lots of trouble

Answers
x=4/tan(20)
Make sure your calculator is in degree mode
What is the product of 234 and 9? 27, 243, 2106, or 1834? (Plz include your working out)
Answers
Hello! :)
Answer:
2,106
Step-by-step explanation:
So let’s see the work:
234x9
First let’s break up 234
Into ones, tens and hundreds.
234
X 9
_____
So we do 4x9=36, we put the 6 in the ones place and have 3 left over
Now do 9x3=27 but...we have to add the 3 which was left over from before
27+3=30, put the zero in the tens place and we have left over 3
9x2=18 now remember to add the 3 from the 30. 18+3=21, put 21 at the hundreds place
So the answer is 2,106
Hope this helps! :)
By, BrainlyMember ^-^
✨ Good luck! ✨
will the sampling distribution of x always be approximately normally distributed? Explain. Choose the correct answer below 0 ?. Yes, because the Central Limit Theorem states that the sampling distribution of x is always approximately normally distributed O B. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough O C. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the population being sampled is normally distributed O D No, because the Central Limit Theorem states that the sampling d bution of x is approximately no aly distribui d only i the sa le sae is mere than 5% of the population.
Answers
B. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough.
The Central Limit Theorem (CLT) is a fundamental concept in statistics that states that as the sample size increases, the sampling distribution of the sample means will approach a normal distribution. However, this is only true if certain conditions are met, one of which is having a large enough sample size.
The CLT states that the sampling distribution of x will be approximately normally distributed if the sample size is large enough (usually greater than 30). If the sample size is small, the sampling distribution may not be normally distributed. In such cases, other statistical techniques like the t-distribution should be used.
Furthermore, the CLT assumes that the population being sampled is not necessarily normally distributed, but it does require that the population has a finite variance. This means that even if the population is not normally distributed, the sampling distribution of x will still be approximately normal if the sample size is large enough.
In conclusion, the answer is B, as the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough.
To learn more about Central Limit Theorem, refer:-
https://brainly.com/question/18403552
#SPJ11
using f(x)=2x^2 and g(x)=3x+4. whats (g of f)(5)?
whats (f of g)(5)?
Answers
Answer:
f(g(x)) = 722, and g(f(x)) = 154
Step-by-step explanation:
f(x) = 2x²
g(x) = 3x + 4
g(f(x)) = 3(2x²) + 4
g(f(5)) = 3(2 × 5²) + 4
g(f(5)) = 3(2 × 25) + 4
g(f(5)) = 3 × 50 + 4
g(f(5)) = 154
f(g(x)) = 2(3x + 4)²
f(g(5)) = 2(3 × 5 + 4)²
f(g(5)) = 2 × 19²
f(g(5)) = 2 × 361
f(g(5)) = 722
Is the vertical component of velocity ever zero? If so, where?
Answers
The vertical component of velocity can be zero at specific points in the motion of an object.
What is Velocity?
Velocity is a vector quantity that describes the rate of change of an object's position in space over time. It is defined as the displacement of an object divided by the time interval during which the displacement occurred.
The vertical component of velocity can be zero at specific points in the motion of an object. This occurs when the object reaches the highest point in its vertical motion and begins to fall back down. At this point, the vertical component of velocity changes direction from upward to downward, and its magnitude becomes zero. This moment is known as the "instant of maximum height" or "instant of maximum altitude." Beyond this point, the vertical component of velocity becomes negative, indicating that the object is moving downward.
To learn more about Velocity, Visit
https://brainly.com/question/80295
#SPJ4
please help me it takes do long to do this please

Answers
Answer:
Step-by-step explanation:
a. (I) x = 65
(ii) vertically opposite angles are equal.
b. (i) 71 degrees
(ii) alternate interior angles are equal
c. (i) z = 180 - 71 = 109 degrees
(ii) angles on a line add up to 180 degrees
Hope this helpsAnswer:
x = 65°, y = 71°, z = 44°
Step-by-step explanation:
x and 65 are vertical angles and congruent, thus
x = 65°
y and 71 are alternate angles and congruent, thus
y = 71°
The sum of the 3 angles in a triangle = 180°, thus
z = 180° - (65 + 71)° = 180° - 136° = 44°
Hence
x = 65°, y = 71° and z = 44°
Identify the sampling technique used in each study. Explain your reasoning. (a) A journalist goes to a campground to ask people how they feel about air pollution (b) For quality assurance, every tenth machine part is selected from an assembly line and measured for accuracy. (c) A study on attitudes about smoking is conducted at a college. The students are divided by class (freshman, sophomore, junior, and senior). Then a random sample is selected from each class and interviewed.
Answers
The sampling technique used in each study is as follows: (a) convenience sampling, (b) systematic sampling, and (c) stratified random sampling.
(a) In the first study, where a journalist goes to a campground to ask people about their feelings regarding air pollution, the sampling technique used is convenience sampling. This is evident because the journalist approaches individuals who are readily available and easily accessible at the campground. However, convenience sampling may introduce bias as it does not ensure a representative sample of the population.
(b) In the second study, where every tenth machine part is selected from an assembly line for measurement, the sampling technique used is systematic sampling. Systematic sampling involves selecting every nth element from a population after establishing a sampling interval. In this case, every tenth machine part is selected to ensure a systematic and unbiased approach to quality assurance.
(c) In the third study, where attitudes about smoking are studied at a college and students are divided by class and then randomly sampled from each class for interviews, the sampling technique used is stratified random sampling. Stratified random sampling involves dividing the population into homogeneous subgroups (strata) and then randomly selecting samples from each subgroup. By dividing the students into different class strata and randomly selecting samples from each class, this study aims to ensure representation from each class in the final sample.
Learn more about sampling technique here:
https://brainly.com/question/31697553
#SPJ11
in a study, researchers wanted to measure the effect of alcohol on the hippocampal​ region, the portion of the brain responsible for​ long-term memory​ storage, in adolescents. the researchers randomly selected 17 adolescents with alcohol use disorders to determine whether the hippocampal volumes in the alcoholic adolescents were less than the normal volume of 9.02 cm3. an analysis of the sample data revealed that the hippocampal volume is approximately normal with x = 8.16 cm3 and and s = 0.7 cm3. conduct the appropriate test at the alpha = 0.01 level of significance.
Answers
The hippocampal volumes in the alcoholic adolescents are significantly less than the normal volume at the alpha = 0.01 level of significance.
The appropriate test to conduct is a one-tailed t-test since the researchers are interested in whether the hippocampal volumes in alcoholic adolescents are less than the normal volume of 9.02 cm3.
Null hypothesis: H0: μ ≥ 9.02 (the hippocampal volumes in the alcoholic adolescents are greater than or equal to the normal volume)
Alternative hypothesis: Ha: μ < 9.02 (the hippocampal volumes in the alcoholic adolescents are less than the normal volume)
The level of significance, α = 0.01, and the degrees of freedom for the t-test are df = n - 1 = 16.
Using a t-table or a t-distribution calculator, the critical t-value for a one-tailed test with α = 0.01 and df = 16 is -2.602.
The test statistic is calculated as:
t = (x - μ) / (s / √(n)) = (8.16 - 9.02) / (0.7 / √(17)) = -2.79
Since the test statistic (-2.79) is less than the critical t-value (-2.602), we reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis.
Therefore, the hippocampal volumes in the alcoholic adolescents are significantly less than the normal volume at the alpha = 0.01 level of significance.
Learn more about hippocampal cells
https://brainly.com/question/14004187
#SPJ4
What fraction form have 6 letters
Answers
Answer:
tenth
Step-by-step explanation:
Please help This is due today help please ASAP

Answers
Answer:
6:05 PM
Step-by-step explanation:
Answer:
6:05 P. M.
Step-by-step explanation:
3 hours after 2:45 pm is 5:45 pm. 20 minutes after 5:45 pm is 6:05 pm.
sec(pi/2 -x) =csc x true or false
Answers
Answer:
true
Step-by-step explanation:
if you rewrite \(sec\left(\frac{\pi }{2}\:-x\right)\) with trigonometric identities:
\(sec\left(\frac{\pi }{2}\:-x\right)\) \(=\frac{1}{\sin \left(x\right)}\)
\(\frac{1}{\sin \left(x\right)}\) \(=\csc \left(x\right)\)
so, yes, \(sec\left(\frac{\pi }{2}\:-x\right)\) \(=\csc \left(x\right)\)
hope this helps!!
(Statistical Measurements MC)
The stem-and-leaf plot displays the distances that a heavy ball was thrown in feet.
2 0, 1, 4
3 1, 2, 6
4 1, 3, 7
5 1, 1
6 5
Key: 3|2 means 3.2
What is the mean, and what does it tell you in terms of the problem?
3.85 feet; The value means that a typical throw of the ball results in 3.85 feet.
3.2 feet; The value means the furthest the ball went.
5.1 feet; The value means this measurement had the most occurrences.
4.62 feet; The value means that a typical throw of the ball results in 4.62 feet.
Answers
The value means that a typical throw of the ball results in 4.62 feet.
Therefore, the correct answer is: 4.62 feet;
To find the mean from the given stem-and-leaf plot, we need to calculate the average of all the distances.
Let's add up all the values and divide by the total number of data points:
(20 + 21 + 24 + 31 + 32 + 36 + 41 + 43 + 47 + 51 + 51 + 56) / 12 = 503 / 12 = 41.92
Rounding to two decimal places, the mean distance is approximately 41.92 feet.
The mean, in this case, tells us the average distance that the heavy ball was thrown.
It represents a typical throw, calculated by summing all the distances and dividing by the number of throws.
In this context, the mean of 41.92 feet indicates the average or typical distance of a throw.
For similar question on distance.
https://brainly.com/question/30395212
#SPJ8
in cubic closest packing, the unit cell is body-centered cubic. true or false
Answers
False. In cubic closest packing (CCP) or face-centered cubic (FCC) structure, the unit cell is not body-centered cubic (BCC). The unit cell in CCP/FCC is composed of a cube with lattice points at the corners and an additional lattice point at the center of each face.
The term "cubic closest packing" refers to the arrangement of atoms or spheres in a cubic lattice where the spheres touch each other along their faces.
This arrangement is achieved by stacking layers of spheres in an ABCABC... pattern. Each sphere is in contact with 12 surrounding spheres, resulting in a coordination number of 12.
On the other hand, the body-centered cubic (BCC) structure has a different arrangement. In BCC, the unit cell consists of a cube with lattice points at the corners and an additional lattice point at the center of the cube. Each atom or sphere in BCC is in contact with eight neighboring atoms.
Therefore, the statement that the unit cell in cubic closest packing is body-centered cubic is false. The correct unit cell for cubic closest packing or face-centered cubic packing is the face-centered cubic (FCC) structure.
To know more about CCP refer here:
https://brainly.com/question/30399141#
#SPJ11
Help Pleaseeee........

Answers
Answer:
5/90
Step-by-step explanation:
5/90 is the answer
I have to put it as a point (x,y)
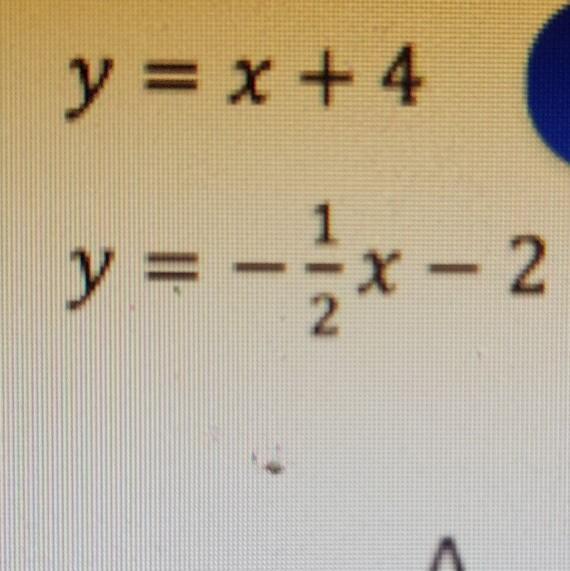
Answers
Answer:
(4,-2) is the answer to that equation.
Answer:
(-4,0)
Step-by-step explanation:
solve for the first variable in one of the equations,then substitute the result into the other equation
what is the main difference in calculations for the independent samples t-test when the variances are equal and the variances are unequal?
Answers
The main difference in calculations for the independent samples t-test when the variances are equal and the variances are unequal is the method used to calculate the pooled variance, the t-value, and the degrees of freedom.
1. When variances are equal (also called pooled variance):
- Calculate the pooled variance using the formula:
\(Sp^2 = [(n1-1) × s1^2 + (n2-1) × s2^2] / (n1 + n2 - 2)\)
- Calculate the t-value using the formula:
\(t = (M1 - M2) / sqrt(Sp^2 × (1/n1 + 1/n2))\)
- Determine the degrees of freedom using the formula:
df = n1 + n2 - 2
2. When variances are unequal (also called Welch's t-test):
- Calculate the t-value using the formula:
\(t = (M1 - M2) / sqrt((s1^2 / n1) + (s2^2 / n2))\)
- Determine the degrees of freedom using the formula:
\(df = [(s1^2 / n1 + s2^2 / n2)^2] / [(s1^2 / n1)^2 / (n1 - 1) + (s2^2 / n2)^2 / (n2 - 1)]\)
In summary, the main difference in calculations for the independent samples t-test when the variances are equal and the variances are unequal is the method used to calculate the pooled variance, the t-value, and the degrees of freedom.
for such more question on t-test
https://brainly.com/question/6589776
#SPJ11
Determine whether each function represents exponential growth or decay. Select the correct option for each function
Answers
Answer:
Determine whether each function represents exponential growth or decay
If a is positive and b is greater than 1 , then it is exponential growth. If a is positive and b is less than 1 but greater than 0 , then it is exponential decay.
Step-by-step explanation:
By analyzing the bases of the exponential equations, we can see that:
Exponential decay Exponential growth.
h(x) = 1.02*(0.06)^2 h(x) = 0.98*(3)^x
h(x) = 4*(0.74)^x h(x) = 9*(1.3)^x
What is exponential function?A general exponential function is written as:
f(x) = A*(b)^x
Where A is the initial value, b is the base, and x is the variable.
An exponential function is an exponential growth if b > 1.
An exponential function is an exponential decay if 0 < b < 1
here, we have,
The first one is:
h(x) = 0.98*(3)^x
The base is b = 3, so this is an exponential growth.
The second one is:
h(x) = 1.02*(0.06)^2
The base is b = 0.06, smaller than 1, then this is an exponential decay.
The third one is:
h(x) = 4*(0.74)^x
The base is b = 0.74, again this is smaller than 1, so we have an exponential decay.
The last one is:
h(x) = 9*(1.3)^x
The base is b = 1.3 > 1, then we have an exponential growth.
Learn more about exponential equations:
brainly.com/question/11832081
#SPJ3