What’s the correct answer for this?

Compute the first two derivative.

\(f(x) = x \sqrt{16 - x^2} = x (16 - x^2)^{1/2}\)

\(f'(x) = x \dfrac{d}{dx} (16 - x^2)^{1/2} + (16 - x^2)^{1/2} \dfrac{d}{dx} x \\\\ ~~~~ = \dfrac x2 (16 - x^2)^{-1/2} \dfrac{d}{dx} (16-x^2) + (16 - x^2)^{1/2} \\\\ ~~~~ = \dfrac x2 (16 - x^2)^{-1/2} (-2x) + (16 - x^2)^{1/2} \\\\ ~~~~ = (16-x^2)^{-1/2} \left(-x^2 + (16 - x^2)\right) \\\\ ~~~~ = \dfrac{16 - 2x^2}{(16 - x^2)^{1/2}}\)

\(f''(x) = \dfrac{(16-x^2)^{1/2} \frac d{dx} (16-2x^2) - (16-2x^2) \frac{d}{dx} (16-x^2)^{1/2}}{\left((16-x^2)^{1/2}\right)^2} \\\\ ~~~~ = \dfrac{(16-x^2)^{1/2} (-4x) - (8-x^2) (16 - x^2)^{-1/2} \frac{d}{dx} (16-x^2)}{16 - x^2} \\\\ ~~~~ = \dfrac{-4x (16-x^2) - (8-x^2) (-2x)}{(16 - x^2)^{3/2}} \\\\ ~~~~ = \dfrac{2x^3-48x}{(16 - x^2)^{3/2}}\)

Take note of the domain of \(f(x)\). We must have \(16-x^2\ge0\) for the square root to be defined, so

\(16 - x^2 \ge 0 \implies x^2 \le 16 \implies |x| \le 4\)

and \(f(x)\) exists only for \(-4 \le x \le 4\).

Intercepts

Set \(x=0\) to find the \(y\)-intercepts. The only one is (0, 0), since

\(f(0) = 0 \sqrt{16-0^2} = 0\)

The first intercept you listed is not a valid intercept. One or both coordinates must be 0.

Set \(f(x)=0\) and solve for \(x\) to find \(x\)-intercepts. We already found (0, 0); there are two others at (-4, 0) and (4, 0).

\(f(x) = x \sqrt{16 - x^2} = 0 \\\\ x = 0 \text{ or } \sqrt{16 - x^2} = 0 \\\\ x = 0 \text{ or } 16 - x^2 = 0 \\\\ x = 0 \text{ or } x^2 = 16 \\\\ x = 0 \text{ or } x = \pm4\)

The instructions say to list these in order from smallest to largest by \(x\)-coordinate first, then by \(y\)-coordinate. So the proper order of the intercepts would be (-4, 0), (0, 0), and (4, 0).

Relative minima/maxima

Find the critical points. We have \(f'(x) = 0\) when

\(f'(x) = \dfrac{16 - 2x^2}{(16 - x^2)^{1/2}} = 0 \\\\ 16 - 2x^2 = 0 \\\\ x^2 = 8 \\\\ x = \pm2\sqrt2 \approx \pm 2.83\)

and \(f'(x)\) is undefined when

\((16 - x^2)^{1/2} = 0 \\\\ 16 - x^2 = 0 \\\\ x^2 = 16 \\\\ x = \pm4\)

Check the sign of the second derivative at the first two critical points.

\(f''(-2\sqrt2) = 4 > 0 \implies \text{rel. min. at }  f(-2\sqrt2) = -8\)

\(f''(2\sqrt2) = -4 < 0 \implies \text{rel. max. at } f(2\sqrt2) = 8\)

For posterity, we should also check the value of \(f(x)\) at the endpoints of the domain.

\(f(-4) = f(4) = 0\)

So \(f(x)\) has a relative minimum at (-2.83, -8) and a relative maximum at (2.83, 8).

Inflection points

We have \(f''(x) = 0\) for

\(f''(x) = \dfrac{2x^3-48x}{(16 - x^2)^{3/2}} = 0 \\\\ 2x^3 - 48x = 0 \\\\ 2x (x^2 - 24) = 0 \\\\ 2x = 0 \text{ or } x^2 - 24 = 0 \\\\ x = 0 \text{ or } x = \pm2\sqrt6\approx\pm4.90\)

The two non-zero solutions fall outside the domain, so the only inflection point is (0, 0).

Answer:

y=3x-8

Step-by-step explanation:

Answer:

0

Step-by-Step Explanation:

The opposite sign of the supplied integer is called additive inverse. (For instance, + becomes - and - becomes +.)

As a result, -2/3 = 2/3 is the additive inverse. (It went from being negative to being positive.)

Let's add them up now.

-2/3 + 2/3 = 0/3 = 0 ( This is because when a number is added to its additive inverse , the numbers cancel out and the sum is 0. )

As a result, the product of -2/3 and its additive inverse (2/3) equals 0. (additive identity).

The slope of the tangent line is:

a = (df(x1)/dx)

The slope of the normal one is:

a' = -1/(df(x1)/dx)

For any function y = f(x), we define the slope of the tangent line at the point x as the derivative evaluated in x.

So if we want to find the slope of the tangent line at the point (x1, y1), we just need to differentiate and evaluate in x1, then the slope will be given by:

df(x1)/dx

And the normal slope is the slope of the perpendicular line, two slopes are perpendicular if the product is -1, then:

a*(df(x1)/dx) = -1

a = -1/(df(x1)/dx)

Where df/dx reffers to the derivative of f(x).

Learn more about tangent lines at:

https://brainly.com/question/30162650

#SPJ1

Answer:

6pi meters

Step-by-step explanation:

The formula for area of a circle is

A = pi r^2

9 pi  = pi r^2

Divide each side by pi

9 = r^2

Take the square root of each side

sqrt(9) = sqrt(r^2)

3 =r

Now we can find the circumference

C = 2 * pi *r

C = 2 * pi *3

C = 6pi meters

Answer:

6pi meters

Step-by-step explanation:

give the person above brainliest

have a good one!

The number of hours (time) after which both Remi and Pam would be exactly 15 miles apart is 3 hours.

First of all, we would have to determine the amount of distance (d) covered by both Remi and Pam.

Mathematically, the distance covered (traveled) by a physical body (object) can be calculated by using this formula:

Distance = speed × time

For the distance covered (traveled) by Remi, we have:

r = 3 × t

r = 3t.

For the distance covered (traveled) by Pam, we have:

p = 4 × t

p = 4t.

Also, the amount of distance (d) covered by both Remi and Pam forms a right-angled triangle as they both jogged East and South respectively. Therefore, there distances can be modeled by Pythagorean theorem:

d = r² + p²

Substituting the parameters into the formula, we have;

15² = 3t² + 4t²

225 = 9t² + 16t²

225 = 25t²

Dividing both sides by 25, we have:

t² = 225/25

t² = 9

t = √9

Time, t = 3 hours.

Read more on distance here: https://brainly.com/question/14697939

#SPJ1

Answer:

-4, -3, -2, -1, 0, 1, and 2

Answer:

-4,-3,-2,-1,0,1,2

Step-by-step explanation:

Answer:

5 hours, and 30 minutes ago, which would be 7:15 AM

Step-by-step explanation:

add hours, then minutes, then subtract both times: 12:45 - 5:30 = 7:15

Answer 25:

Step-by-step explanation:

x int = 15

y int = -10

y intercept can be found bt setting X to 0

x intercept can be found by setting Y to 0

2(0) - 3y = 30 --> -3y = 30 --> y = -10

2x - 3(0) = 30 --> 2x = 30 --> x = 15

alternatively, y int is "b" in eq. y = mx + b

-3y = 30 -2×

y = -10 + (2/3)x

y = (2/3)x - 10

b = -10

Using  the associative law of multiplication we get this two solution of the given expression: (12x)y = (12 * x) * y , (12x)y = 12 * (x * y)

The associative law of multiplication states that when multiplying three or more numbers, the product is the same regardless of the order in which the numbers are grouped. In other words, it doesn't matter which numbers we multiply first, the result will be the same.

Using the associative law of multiplication, we can group the factors in any way we like. Therefore, we can write an equivalent expression to (12x)y by changing the grouping of factors.

One way to group the factors is to group the two numerical coefficients (12 and y) together.

Another way to group the factors is to group the variable x and the coefficient y together.

Both of these expressions are equivalent to (12x)y and they all follow the associative law of multiplication.

For such more questions on associative law

https://brainly.com/question/30034923

#SPJ8

Answer:

192 in cubed

Step-by-step explanation:

Multiply 12*2= 24*8

Answer:

192 should be yyour answer

Step-by-step explanation:

There is a 'strike-through' root at -1 and a double root at 2, so the equation is of the form

\(y=a(x+1)^3 (x-2)^2\)

Since the y-intercept is 4,

\(4=a(0+1)^3(0-2)^2 \implies 4a=4 \implies a=1 \\ \\ \therefore \boxed{y=(x+1)^3 (x-2)^2}\)

Answer:

m

Step-by-step explanation:

mmm

Answer:

The answer is 7680

Step-by-step explanation:

First you multiply 32 by 4(the usual formula) which gives you 128. However, the time changes the some things. So then you must multiply 128 by 60 (60 minutes in one hour). Which gives you 7680

hope i helped :D

Answer:

The remainder is \(4\).

The quotient is \(3x^{2}+6x+1\)

Step-by-step explanation:

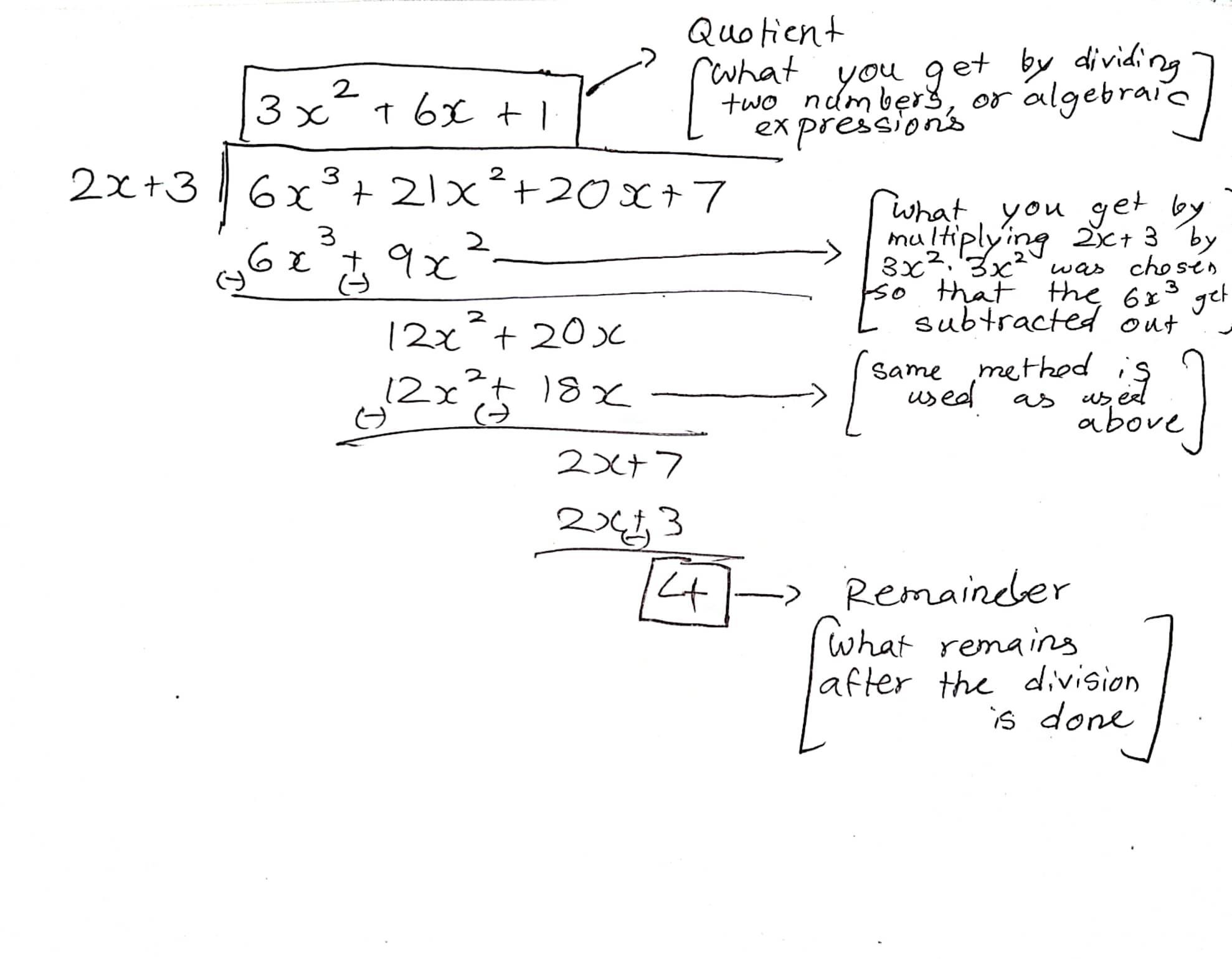
Step 1: Do long division

To divide these expressions, we will have to make use of long division, which is shown in the picture.

Step 2: Identifying the remainder and quotient

The remainder is \(4\).

The quotient is \(3x^{2}+6x+1\)

Answer:

2

Step-by-step explanation:

Answer:

B. x = 4 and x = -10

Step-by-step explanation:

First, expand the equation

(x + 3)² = 49

(x + 3)(x + 3) = 49

x² + 6x + 9 = 49

Subtract 49 from both sides

x² + 6x -40 = 0

Factor

(x + 10)(x - 4) = 0

Solve

x + 10 = 0

x = -10

x - 4 = 0

x = 4

So, the correct answer is B. x = 4 and x = -10

The value of the number is x = 34.

Let's break down the problem and solve it step by step.

1. "Five less than twice the value of a number": This can be represented as 2x - 5, where x is the number.

2. "Three times the quantity of 4 more than 1/2 the number": This can be represented as 3 * (x/2 + 4).

According to the problem statement, the two expressions are equal. We can set up the equation as follows:

2x - 5 = 3 * (x/2 + 4)

Now, let's solve the equation:

2x - 5 = 3 * (x/2 + 4)

Distribute the 3 to both terms inside the parentheses:

2x - 5 = (3/2)x + 12

Multiply through by 2 to eliminate the fraction:

2(2x - 5) = 2((3/2)x + 12)

4x - 10 = 3x + 24

Next, let's isolate the x term by moving the constant terms to the other side of the equation:

4x - 3x = 24 + 10

Simplify:

x = 34

For more such questions on number,click on

https://brainly.com/question/24644930

#SPJ8

The linear program shows that there are different attainable arrangements that accomplish the same ideal objective function value..

Based on the given data, since the objective function values at the five corner points are diverse, able to conclude that there's no one-of-a-kind ideal arrangement for this linear program.

The reality that there are numerous distinctive objective function values at the corner points suggests that there are numerous ideal arrangements or that the objective work isn't maximized or minimized at any of the corner points.

In this case, the linear program may have numerous ideal arrangements, showing that there are different attainable arrangements that accomplish the same ideal objective function value.

Learn more about Objective function value here:

https://brainly.com/question/14309521

#SPJ1

Answer:

We are 95% confident that the true proportion of U.S. adults who live with one or more chronic conditions is between 39.7% and 46.33%

Step-by-step explanation:

From the question we are told that

  The  sample  proportion is \(\r p = 43\%  = 0.43\)

   The  standard error is \(SE =  0.017\)

Given that the confidence level is 95%  then the level of significance is mathematically represented as  

      \(\alpha =  (100-95)\%\)

=>   \(\alpha = 0.05\)

Generally from the normal distribution table the critical value  of  \(\frac{\alpha }{2}\) is  

   \(Z_{\frac{\alpha }{2} } =  1.96\)

Generally the margin of error is mathematically represented as

     \(E = Z_{\frac{\alpha }{2} } *  SE\)

=>    \(E = 1.96 *  0.017\)

=>     \(E = 0.03332 \)

Generally 95% confidence interval is mathematically represented as

      \(\r p -E <  p <  \r p +E\)

=>   \(0.43 -0.03332 <  p <  0.43 + 0.03332\)

=>    \( 0.39668 <  p <  0.46332\)

Converting to percentage

\( (0.39668 * 100)<  p <  (0.46332*100)\)        

\( 39.7\% <  p < 46.33 \%\)    

Answer:

Solving the radical \(\pm\sqrt{-81}\)  we get \(\mathbf{\pm9 \ i}\)

Step-by-step explanation:

We need to express the radical \(\pm\sqrt{-81}\) using the imaginary unit i

Prime factors of 81 are: 3x3x3x3

and \(\sqrt{-1}=i\)

Solving:

\(\pm\sqrt{-81}\\=\pm\sqrt{81}\sqrt{-1}\\=\pm\sqrt{3\times3\times3\times3}i\\ =\pm\sqrt{3^2\times3^2}i\\=\pm3\times3\ i\\=\pm9 \ i\)

So, Solving the radical \(\pm\sqrt{-81}\)  we get \(\mathbf{\pm9 \ i}\)

The vertex of the graph is a maximum at (-2, 4)

From the question, we have the following parameters that can be used in our computation:

The graph

The graph is a quadratic function

From the graph, we can see that the graph has a maximum value

This maximum value represents the vertex of the graph

And it is located at (-2, 4)

So, we have

Maximum = (-2, 4)

Hence, the maximum value of the function is (-2, 4)

Read more about vertex at

brainly.com/question/28180581

#SPJ1

Answer:

EXPLAIN

Step-by-step explanation:EXPLAIN

EXAMPLE

Answer:

Set your calculator to Degree mode.

a² = 17² + 20² - 2(20)(17)cos(89°)

a² = 677.13236

a = 26.0 in.

sin(89°)/26.02177 = (sin B)/17

sin B = 17sin(89°)/26.02177

B = 40.8°

C = 50.2°

Answer:

b

Step-by-step explanation:

-a-(a-b)

Distribute the negative sign to get -a+a+b

-a cancels out a, and you're left with b.

Answer:a²-ab

Step-by-step explanation:

since the negative symbol is on the outside of the parenthesis all values inside the parenthesis get reversed. so:

-a(-a+b)

Then multiply by -a:

a²-ab

Answer:

Most likely C

Step-by-step explanation:

where's is the other info. If no there info is provided then its most likely c because there's an obvious relationship. If I didn't help delete my answer thx.

Answer:

-1 6/10

is greater than

- 5/3

Step-by-step explanation: