Whats the InversE of Y=3x+2
Answers
Related Questions
Find the lateral surface area of the cylinder. Use 3.14 for π.
will make brainliest if answer correctly with work
Answers
The lateral surface area of the cylinder is 344.64 centimeter square
The radius of the cylinder = 4.9 centimeter
The height of the cylinder = 11.2 centimeter
The lateral surface area of the cylinder = 2 × π × r × h
Where r is the radius of the cylinder
h is the height of the cylinder
The value of π = 3.14
Substitute the values in the equation and find the lateral surface area of the cylinder
The lateral surface area of the cylinder = 2 × 3.14 × 4.9 × 11.2
Multiply the terms
= 344.64 centimeter square
Therefore, the lateral surface area is 344.64 centimeter square
Learn more about lateral surface area here
brainly.com/question/11385509
#SPJ4
The given question is incomplete, the complete question is:
Find the lateral surface area of the cylinder. Use 3.14 for π.

Use a geometric tool to draw a circle. Draw and measure a radius and a diameter of the circle .
Answers
Answer:
Attached is an example of a circle with a radius of 5 and a diameter of 10.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

Solve the trigonometric equation: 5sin theta+3=0 for values of theta from 0° to 360
Answers
Answer:
126.9° and 323.°1
Step-by-step explanation:
I'll use x instead of theta and you can replace it by theta
5 sin x + 3 = 0
5 sin x = - 3
Sin x = - 3/5
Key angle = sin¯¹ 3/5 = 36.8698
Sin negative, so we use the third and fourth quadrants
X = 90+36.8698, 360-36.8698
X = 126.8698, 323.1302
Theta = 126.9°, 323.°1
Guys please help! i will mark brainliest to the right answers
Note: in order for me to mark a brainliest 2 people need to answer

Answers
Answer: \(\frac{3}{2}x+y=-\frac{17}{2}\)
Step-by-step explanation:
The standard form of a linear equation is \(ax+by=c\)
So we need to solve for c
Start by simplifying everything in the equation
\(y+7=-\frac{3}{2} (x+1)\)
Use the Distributive Property
\(y+7=-\frac{3}{2}x-\frac{3}{2}\)
Now subtract 7 from both sides
\(y+7=-\frac{3}{2}x-\frac{3}{2}\\y+7-7=-\frac{3}{2}x-\frac{3}{2}-7\\y=-\frac{3}{2}x-\frac{17}{2}\)
Add \(\frac{3}{2} x\) to both sides
\(y+\frac{3}{2}x=-\frac{3}{2}x+\frac{3}{2}x-\frac{17}{2}\\\frac{3}{2}x+y=-\frac{17}{2}\)
NOTE: \(-\frac{17}{2}\) simplifies to -8.5 if you find that more desirable
Christian opened a savings account with $3250. His account will earn 5.2% simple interest.
How much money will be in his account after 6 years?
Answers
The total amount of money will be in his account after 6 years is $4264.
Given that, principal = $3250, rate of interest = 5.2% and time period = 6 years.
What is the simple interest?Simple interest is a method to calculate the amount of interest charged on a sum at a given rate and for a given period of time.
Simple interest is calculated with the following formula: S.I. = P × R × T, where P = Principal, R = Rate of Interest in % per annum, and T = Time, usually calculated as the number of years.
Substitute P=$3250, R=5.2% and T=6 years in simple interest formula
That is, S.I. = (3250 × 5.2 × 6)/100
= $1014
Amount = Principal + Simple interest
= 3250 + 1014
= $4264
Therefore, the total amount of money will be in his account after 6 years is $4264.
To learn more about the simple interest visit:
https://brainly.com/question/25845758.
#SPJ6
Find the arc length of the partial circle.
Either enter an exact answer in terms of \piπpi or use 3.14 π and enter your answer as a decimal.

Answers
Answer:
arc = 7.5π units
Step-by-step explanation:
the arc length is calculated as
arc = circumference of circle × fraction of circle
the angle subtended at the centre by the arc is 360° - 90° = 270° , then
arc = 2π × 5 × \(\frac{270}{360}\)
= 10π × \(\frac{3}{4}\)
= \(\frac{30\pi }{4}\)
= 7.5π
15. Many people swimming in a pool experience pain in their ears if they dive to the
bottom. Why is this?
A. Pressure increases as the depth of the water column above them increases.
B. The area of the pool is wider where it's deeper.
C. Pressure decreases as the depth of the water column above them increases.
D. The vapor pressure at the surface is removed.
Answers
Answer:
The answer is Ahope this helps
Give the value of x.
128 2x
Answers
Which statement describes A′B′?

Answers
Answer:
1 answer to your question
Solve for y.
(4y + 5) (-2y + 3) = -3-7y - 8y2 +9y - 9

Answers
Step-by-step explanation:
hope this will help you......

Answer:
\((4y + 5)( - 2y + 3) =-3 -7y - 8 {y}^{2}+9y - 9 \\ - 8 {y}^{2} + 12y - 10y + 15 = - 12 + 2y - 8 {y}^{2} \\ - 8 {y}^{2} + 2y + 15 = - 12 + 2y - 8 {y}^{2} \)
value of y is getting cancelled outso value of y does not exist.HELP ASAP
The histogram below shows information about the hours students spent exercising in a week:
A histogram is titled Weekly Exercise, the horizontal axis is labeled Hours of Exercise, and the vertical axis is labeled Students. The range on the horizontal axis is 0 to 4, 5 to 9, and 10 to 14. The values on the vertical axis are from 0 to 10 at intervals of 1. The first bin goes to 4, the second bin to 9, the third bin to 5.
Which information is provided in the histogram? (4 points)
a
The number of students who exercised 4 hours or more
b
The number of students who exercised 9 hours or fewer
c
The mean hours of exercise
d
The median hours of exercise

Answers
The information from the histogram are as follow,
Students exercised for 4 or more hours are 14.
Students exercised for 9 or fewer hours are 13.
Mean of the data = 7.3.
median of the data = 6.33.
The histogram provides information about the distribution of hours students spent exercising in a week.
The number of students who exercised 4 hours or more,
= adding up the counts in the first and second bins.
= 9 + 5
= 14 students
The number of students who exercised 9 hours or fewer,
= adding up the counts in the first and second bins
= 9 + 4
= 13 students
The mean hours of exercise is not provided by the histogram
use the formula,
Mean = Σ\(x_{i} y_{i}\) / N
where
\(x_{i}\) is the midpoint of the ith bin
\(y_{i}\) is the frequency of the ith bin
N is the total sample size
Mean = [(2)(4) + (7)(9) + (12)(5)] / 18
= 7.3
The median hours of exercise is not provided by the histogram.
Median = L + ( (n/2 – F) / f ) × w
where
L=The lower limit of the median group
n = The total number of observations
F = The cumulative frequency up to the median group
f =The frequency of the median group
w = The width of the median group
median = 5 + ( ( 14/2 - 4 ) /9 × 4
= 6.33
Therefore, from the histogram the number of students exercised for ,
4 hours or more are 14.
9 hours or fewer are 13.
mean = 7.3
Median = 6.33
learn more about histogram here
brainly.com/question/9696858
#SPJ1
calculate the following 2+2
Answers
Answer:4
Step-by-step explanation:
2+2 is 4
Multiply: -12y(y - 6) Enter the correct answer.
Answers
(-12y x y) -(-12y x -6)
= 12y^2 +72y
2x-1=y
3x-1=y
Consider the system of equations above. Which of the following statements about this system is true?

Answers
Answer:
B; There is only one (x,y) solution and y is negative
Step-by-step explanation:
First, I graphed the two equations. Attached is an image of the equations graphed. Next, I looked for overlapping points. Wherever the two points overlap, there is a solution. When looking at the graph, we can see the lines overlap at only one point, (0,-1). Since y is negative, the answer must be B; there is only one (x,y) solution and y is negative.
If this answer helped you, please leave a thanks!
Have a GREAT day!!!

How to solve and answer

Answers
Answer:
D. (-2, 0) and (3, 0).
Step-by-step explanation:
At the x -intercepts the function = 0, so
(2x + 4)(x - 3) = 0
2x + 4 = 0 and x - 3 = 0
x = -4/2 = -2 and x = 3.
So they are (-2, 0) and (3, 0).
x = 3 or x = -2
Step-by-step explanation:
f(x) = (2x + 4)(x - 3)
y = (2x + 4)(x - 3)
x - intercept occurs when y = 0
0 = (2x + 4)(x - 3)
0 = 2x² - 6x + 4x - 12
2x² - 2x - 12 = 0
(2x² - 2x - 12)/2 = 0/2
x² - x - 6 = 0
From the quadratic formula,
x = (-b +- √(b² - 4ac))/2a
x = (- ( -1 ) +- √(( -1)² - 4( 1 )( -6 )))/2( -1 )
x = (1 +- √(1 - ( -24)))/-2
x = (1 +- √25)/-2
x = (1 +- 5)/-2
x = 3 or x = -2
Review the graph.
On a coordinate plane, a circle has center (4, 0) and radius 4. Another circle has center (2, negative 3) and radius 6. The area inside of the first circle and outside of the second circle between the 2 circles is shaded.
Which system of inequalities is shown in the graph?
36 > (x + 3)2 + (y – 2)2 and 16 > (x – 4)2 + y2
36 > (x – 2)2 + (y + 3)2 and 16 > (x – 4)2 + y2
36 < (x + 3)2 + (y – 2)2 and 16 > (x – 4)2 + y2
36 < (x – 2)2 + (y + 3)2 and 16 > (x – 4)2 + y2

Answers
Answer:
36 < (x - 2)² + (y + 3)² and 16 > (x - 4)² + y²
Step-by-step explanation:
This is because the shaded area is inside the first circle (centered at (4, 0) with a radius of 4) but outside the second circle (centered at (2, -3) with a radius of 6). The inequalities reflect these conditions by setting the inequality signs accordingly. The inequality with "<" for the first circle ensures that the shaded area is within the circle, and the inequality with ">" for the second circle ensures that the shaded area is outside the circle.
if 3 -letter words'' are formed using the letters a, b, c, d, e, f, g, how many such words are possible for each of the following conditions:
Answers
The possible number of 3 -letter words that can be formed with given conditions.
(a) No condition is imposed: 343
(b) No letter can be repeated in a word: 210
(c) Each word must begin with the letter 'a' : 49
(d) The letter 'c' must be at the end: 49
(e) The second letter must be a vowel: 98
In this question we have been given that 3 -letter words' are formed using the letters a, b, c, d, e, f, g.
We need to find the possible number of 3 -letter words that can be formed with given conditions.
(a) No condition is imposed.
the possible number of 3 letters words would be,
7³ = 343
(b) No letter can be repeated in a word.
Using the formula of Permutation,
^{7}P_3 = 7!/(7 - 3)!
= 210
(c) Each word must begin with the letter a.
If each word begins with letter 'a' there would be possible combinations of remaining 6 letters at 2nd and 3rd position of 3-letter word.
So, the possible number of 3 letters words would be,
7² = 49
(d) The letter c must be at the end.
If each word ends with letter c there would be possible combinations of remaining 6 letters at 1st and 2nd position of 3-letter word.
So, the possible number of 3 letters words would be,
7² = 49
(e) The second letter must be a vowel.
In the 3 letter word, the second letter must be vowel which is either a or e.
So, the possible number of 3 letters words would be,
49 + 49 = 98
Therefore, the possible number of words would be (a) No condition is imposed: 343
(b) No letter can be repeated in a word: 210
(c) Each word must begin with the letter 'a' : 49
(d) The letter 'c' must be at the end: 49
(e) The second letter must be a vowel: 98
Learn more about permutation here:
https://brainly.com/question/28720645
#SPJ4
The complete question is:
3 -letter words'' are formed using the letters a, b, c, d, e, f, g. How many such words are possible for each of the following conditions?
(a) No condition is imposed.
(b) No letter can be repeated in a word.
(c) Each word must begin with the letter a.
(d) The letter c must be at the end.
(e) The second letter must be a vowel.
What are the dimensions, a, b, and c, of the net? a = cm b = cm c = cm
Answers
In an attempt to clean up your room, you have purchased a new floating shelf to put some of your 17 books you have stacked in a corner. These books are all by different authors. The new book shelf is large enough to hold 10 of the books.
(a) How many ways can you select and arrange 10 of the 17 books on the shelf? Notice that here we will allow the books to end up in any order. Explain.
(b) How many ways can you arrange 10 of the 17 books on the shelf if you insist they must be arranged alphabetically by author? Explain.
Answers
Answer:
19448 ways
70572902400 ways
Step-by-step explanation:
(a)
To arrange 17 books on a shelf from a possible we use the combination formula :
nCr = n! ÷ (n-r)!r!
17C10 = 17! ÷ 7! 10!
17C10 = 19448 ways
To arrange the books in alphabetical order :
2)
In question, 2, the order of arrangement matters ; hence, we use permutation ;
nPr = n! ÷ (n-r)!
17P10 = 17! ÷ (17 - 10)! = 17! ÷ 7!
17P10 = 70572902400
A research study indicated a negative linear relationship between two variables: the number of hours per week spent exercising (exercise time) and the number of seconds it takes to run one lap around a track (running time). Computer output from the study is shown below.
A figure of a computer output is shown. At the top is a table with two rows. The first row reads variable, N, mean, S E mean, and standard deviation. The second row reads running time, 11, 74.81, 2.21, and 7.33. Below this is a second table with three columns labeled predictor, coefficient, and S E coefficient. The first row reads constant, 88.01, and 0.49. The second row reads exercise time, negative 2.20, and 0.07. At the bottom it reads S equals 0.76 and R squared equals 99 percent.
Assuming that all conditions for inference are met, which of the following is an appropriate test statistic for testing the null hypothesis that the slope of the population regression line equals 0 ?
Answers
Answer:
The appropriate test statistic for testing the null hypothesis that the slope of the population regression line equals 0 is the t-statistic.
The t-statistic for testing the slope coefficient is calculated as follows:
t = (b1 - 0) / SE(b1)
where b1 is the estimated slope coefficient, and SE(b1) is the standard error of the estimated slope coefficient.
From the computer output, we see that the estimated slope coefficient for exercise time is -2.20, and the standard error of the estimated slope coefficient is 0.07.
Therefore, the t-statistic is:
t = (-2.20 - 0) / 0.07 = -31.43
This t-statistic follows a t-distribution with n-2 degrees of freedom, where n is the sample size. The sample size is not given in the output, so we cannot determine the exact degrees of freedom.
How far would the plane fly in t hours at this speed
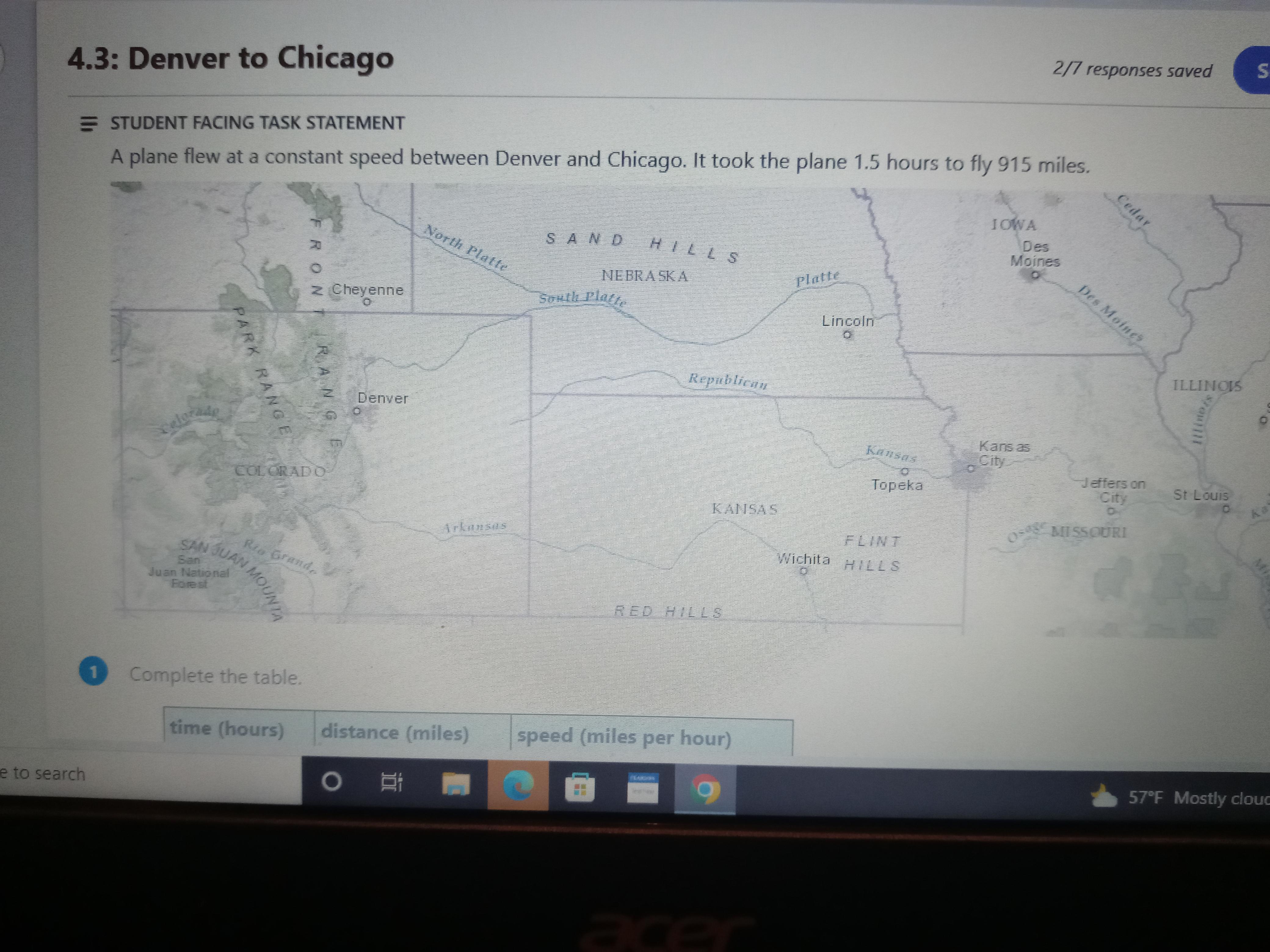
Answers
Answer: 610 MPH
Step-by-step explanation:
915 divided by 1.5=610 MPH
610 divided by 2=305 MP Half n Hour
610+305=915
points that don't belong to any line

Answers
Answer:
Noncollinear points
Step-by-step explanation:
Collinear points lie on the same line. Noncollinear points are the opposite.
Question 10
Five numbers are described below.
Drag the values described into the correct order from LEAST to GREATEST. Use the number line as needed to help you order the values.

Answers
Answer:
the opposite of the opposite of -9, the opposite of 6, the opposite of 4, the opposite of 0, the opposite of the opposite of 7
Explanation:
the opposite of 4 = -4
the opposite of the opposite of -9 = -9
the opposite of 6 = -6
the opposite of the opposite of 7 = 7
the opposite of 0 = 0
Then you just put them in order.
Hope this helps!
Please help and I need you to explain why but I’m the simplest way possible :)

Answers
Answer:
Parallelogram
Step-by-step explanation:
Observation 1:
the sides do not have the same measure √53≠√68 so is NOT a square and NOT a rhombus
Observation 2:
the opposite sides are congruent
AB=CD=√53, and BC=DA=√68
Observation 3:
lines that have the same slope are parallel so opposite sides are also parallel
slope of AB =slope of CD =-2/7, and slope of BC=slope of DA=8/2
so we have 2 pair of sides congruent and parallel but to decide if is a parallelogram or rectangle we need to see if the adjacent sides form 90° or not
Observation 4:
lines that are perpendicular form 90° and their slope is negative reciprocal.
AB slope =-2/7 and slope of BC =8/2 so are NOT perendicular therefore is a parallelogram
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
helo please show work

Answers
Answer:
Step-by-step explanation:
Solution:
We can simplify the ratio 305 : 60 by dividing both terms by the greatest common factor (GCF).
The GCF of 305 and 60 is 5.
Divide both terms by 5.
305 ÷ 5 = 61
60 ÷ 5 = 12
Therefore:
305 : 60 = 61 : 12
URGENT!!!! Find the y-intercept of the line that passes through the points (-3, 7) and (3, −9).
Answers
Answer:
\(m = \frac{ - 9 - 7}{3 - ( - 3)} = \frac{ - 16}{6} = - \frac{8}{3} \)
\(7 = - \frac{8}{3} ( - 3) + b\)
\(7 = 8 + b\)
\(b = - 1\)
\(y = - \frac{8}{3} x - 1\)
The y-intercept is -1.
Help Quickly! A truck needs 7 gallons of fuel to travel 56 miles. Can the truck travel 48 miles with 6 gallons of fuel? Explain.
Giving brainliest

Answers
Yes, 7/56 and 6/48 are proportional because 7×48 = 56×6. Therefore, the correct answer is option B.
Given that, a truck needs 7 gallons of fuel to travel 56 miles.
The truck travel 48 miles with 6 gallons of fuel.
Here, the proportion is
7:56::6:48
We know that, the proportion is product of extremes = product of means
7×48 = 56×6
336 = 336
Therefore, the correct answer is option B.
To learn more about the proportional relationship visit:
brainly.com/question/12917806.
#SPJ1
what is the probability that either event will occur?

Answers
The probability that either event will occur is P ( C ) = 0.89
Given data ,
Let the probability that either event will occur be P ( C )
P ( A ) = 20/36
P ( B ) = 12/36
where P ( A or B ) = P ( C )
P ( C ) = P ( A ) + P ( B )
P ( C ) = 32/36
P ( C ) = 0.88888
Hence , the probability is P ( C ) = 0.89
To learn more about probability click :
https://brainly.com/question/17089724
#SPJ1
Determine g(x + a) – g(x) for the following function.
g(x) = 5x2 + 2x
Answers
Answer:
\(g(x + a) - g(x) = 10ax + 5a^2 + 2a\)
Step-by-step explanation:
We are given the function:
\(g(x) = 5x^2 + 2x\)
And we want to determine:
\(\displaystyle g(x+a) - g(x)\)
Substitute:
\(\displaystyle \begin{aligned}g(x + a) - g(x) &=\left[5(x+a)^2 + 2(x+a)\right] -\left[5x^2+2x\right] \end{aligned}\)
And simplify:
\(\displaystyle \begin{aligned}g(x + a) - g(x) &=\left[5(x+a)^2 + 2(x+a)\right] -\left[5x^2+2x\right] \\ \\ &= \left(5(x^2 + 2ax + a^2) + (2x + 2a) \right) + \left(-5x^2 - 2x\right) \\ \\ &= \left((5x^2 + 10ax + 5a^2) + (2x + 2a)\right) + \left(-5x^2 - 2x\right) \\ \\ &= (5x^2-5x^2) + (10ax + 2x - 2x) + (5a^2+2a) \\ \\ &= 10ax + 5a^2 + 2a \end{aligned}\)
In conclusion:
\(g(x + a) - g(x) = 10ax + 5a^2 + 2a\)