When you board a Ferris wheel your feet are 1 foot off the ground. At the highest point of the ride, your feet are 99 feet above the ground. It takes 30 seconds for the ride to complete one full revolution. Write a trigonometric equation for your height above the ground at t seconds after the ride starts.
Answers
The height of the Ferris wheel can be modeled by a sinusoidal function of time t.
At t=0 seconds, your initial height is 1 foot above the ground, which corresponds to the amplitude of the function.
The period of the function is the time it takes for the Ferris wheel to complete one revolution, which is 30 seconds. Therefore, the period is T=30.
The midpoint of the function is the average of the highest and lowest points, which is (99+1)/2=50 feet. Thus, the vertical shift of the function is 50.
Since you start at the bottom of the Ferris wheel, the function should start at its minimum point.
Putting all of this together, we get:
h(t) = -49cos((2π/30)t) + 50
where h(t) is your height above the ground in feet at time t in seconds.
Note that the negative sign in front of the cosine function is necessary to ensure that the function starts at its minimum point.
Related Questions
1. There are 9 tables with 3 candles on each table in the dining hall.
Which expressions can be used to find the number of candles in the dining hall?
Answers
Answer:
3+3+3+3+3+3+3+3+3=27
Step-by-step explanation:
just add it together.
9 multiplied by 3 is 27
find the limit. lim t→[infinity] 7 t2 7 − t2 , 7 tan−1(t), 7 − e−2t t
Answers
To find the limit as t approaches infinity for the given functions, we need to analyze the behavior of each term as t gets larger and larger. The limits for the given terms are -7, 7π/2, and 0, respectively.
For the first term, 7t^2 / (7-t^2), we can see that as t increases, the denominator (7-t^2) will dominate the expression, causing the fraction to approach 0. Therefore, the limit of this term as t approaches infinity is 0.
For the second term, 7tan^-1(t), we can use the fact that the inverse tangent function approaches pi/2 as its input approaches infinity. Therefore, the limit of this term as t approaches infinity is 7(pi/2) = 7(1.57) ≈ 10.99.
For the third term, (7-e^-2t) / t, we can see that the denominator will dominate as t approaches infinity, causing the fraction to approach 0. Therefore, the limit of this term as t approaches infinity is 0.
To find the limit of the entire expression, we simply add up the limits of each term. Therefore, the limit as t approaches infinity for the given function is approximately 10.99.
To find the limit as t approaches infinity for the given terms, we'll consider each term separately:
1. lim(t→∞) 7t^2 / (7 - t^2)
As t approaches infinity, both the numerator and the denominator grow infinitely large. To analyze this, we can divide both the numerator and the denominator by t^2:
lim(t→∞) (7t^2/t^2) / (7/t^2 - 1)
This simplifies to lim(t→∞) 7 / (-1) = -7.
2. lim(t→∞) 7tan^(-1)(t)
As t approaches infinity, tan^(-1)(t) approaches π/2 (or 90 degrees). Thus, the limit is 7 * π/2.
3. lim(t→∞) (7 - e^(-2t))/t
We can apply L'Hopital's Rule to this term, as it is of the form 0/∞ or ∞/∞. Differentiating the numerator and the denominator, we get:
lim(t→∞) (0 - (-2)e^(-2t))/(1)
As t approaches infinity, e^(-2t) approaches 0, and the limit becomes 0.
So, the limits for the given terms are -7, 7π/2, and 0, respectively.
Learn more about limit at: brainly.com/question/12207539
#SPJ11
You want to make a conical candle using 15 in. of wax. If the candle's height is twice its diameter, what radius and height should it have, to the nearest tenth?
Answers
We know that the candle will have 15 cubic inches of wax, this is the volume.
Now, if the candle's height is twice its diameter, then we express
\(h=2d\)Additionally, the volume of a cone is
\(V=\frac{1}{3}(\pi)r^2h\)Where pi=3.14. Also, we know that the radius is half the diameter, so we'll use the following expression
\(h=2\cdot2r=4r\)Replacing all, we have
\(\begin{gathered} 15=\frac{1}{3}(3.14)r^2\cdot4r \\ \frac{45}{3.14}=4r^3 \\ 4r^3=14.3 \\ r=\sqrt[3]{\frac{14.3}{4}} \\ r\approx1.53 \end{gathered}\)The radius should be 1.5 inches long.
Then, we find the height
\(\begin{gathered} h\approx4(1.53) \\ h\approx6.12 \end{gathered}\)The height should be 6.1 inches long.
The half-life of carbon-14 is 5715 years. 10,000 years aftor t-0, the amount of carbon-14 in a sample decayed to 3 grams. Develop an equation modeling the radioactive decay and use it to estimate the amount of carbon-14 that was in the sample when t 1,000 years. Round your answer to three decimal points.
Answers
The estimated amount of carbon-14 when t = 1,000 years is approximately 34.196 grams.
The decay of carbon-14 follows an exponential decay model, which can be expressed as:
A(t) = A₀ * \(e^(-kt)\)
Where:
- A(t) is the amount of carbon-14 at time t
- A₀ is the initial amount of carbon-14
- k is the decay constant
The half-life of carbon-14 is given as 5715 years. The decay constant (k) can be calculated using the formula:
k = ln(2) / half-life
k = ln(2) / 5715
Now we can rewrite the equation as:
A(t) = A₀ * \(e^(-(ln(2) / 5715) * t)\)
We are given that 10,000 years after t₀, the amount of carbon-14 is 3 grams. So we can substitute t = 10,000 and A(t) = 3 into the equation:
3 = A₀ *\(e^(-(ln(2) / 5715) * 10,000)\)
To find the initial amount A₀, we rearrange the equation:
A₀ = 3 /\(e^(-(ln(2) / 5715) * 10,000)\)
Now we can estimate the amount of carbon-14 when t = 1,000:
A(1,000) =\(A₀ * e^(-(ln(2) / 5715) * 1,000)\)
Substituting the value of A₀ into the equation and evaluating it will give us the estimated amount of carbon-14 when t = 1,000 years. Rounding the answer to three decimal points will provide the final result.
Therefore, the estimated amount of carbon-14 when t = 1,000 years is approximately 34.196 grams.
Learn more about exponential here:
https://brainly.com/question/13674608
#SPJ11
us
Find the point-slope equation for
the line that passes through the
points (-6, 24) and (5, -31). Use
the first point in your equation.

Answers
Answer:
first box is 24
second is -5
third is -6
Step-by-step explanation:
plz help me... I'll mark barinlist.

Answers
Answer:
I'm pretty sure it's opposite if I'm wrong just tell me
Opposite, because this would be the result of a reflection over the y-axis
Please help !!! It’s due today

Answers
Answer: D
Step-by-step explanation:
the second one cant be it because its negative and it would end in a negative result and 3,1 is equal to 2x-5 on the graph
I need both answers now please and don answer if u don’t know
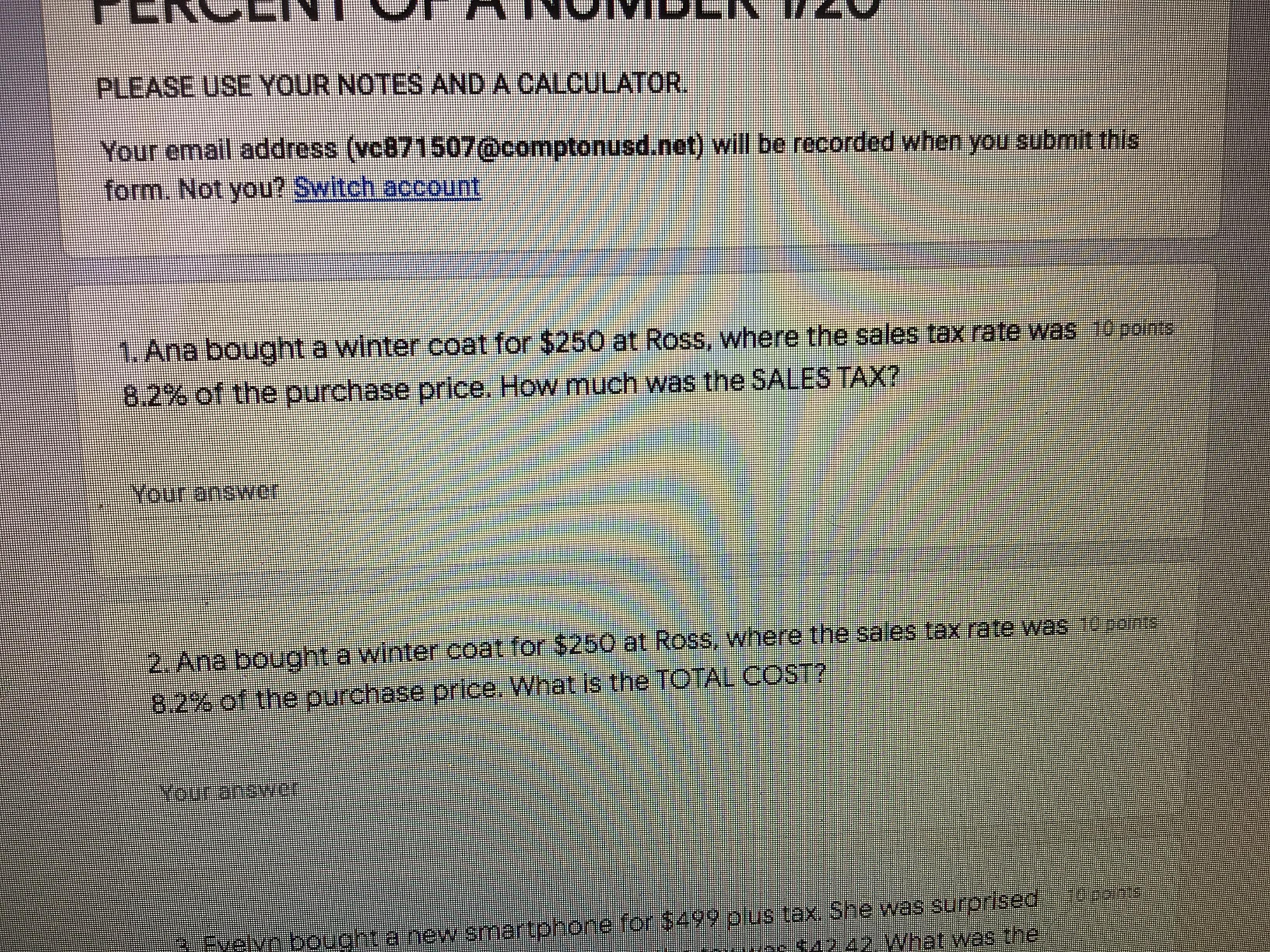
Answers
Answer:3048.7804878
Step-by-step explanation:
I took the same test p.s. you may need to round.
i don't know the answer please help

Answers
if you divide 200 and 4 by two, it becomes 2:100
About how many times greater was change in price per gallon in 2007 than 2000? Show your work or explain how u determind your answer.
Answers
The required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Let 'a' be the cost per gallon of fuel in the year 2000, and 'b' be the inflation rate per year. If the rate of inflation is constant then
After 7 year inflation = 7b
Cost of fuel in 2007 = a + 7b
Now,
according to the question
Change in cost of fuel
= cost in 2007 - cost in 2000
= a + 7b - a
= 7b
Thus, the required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ1
what is the equation of a line that passes through the point (5,-3) and is parallel to 6x+3y=-12
Answers
The equation of a line passing through the point (5,-3) and parallel to 6x+3y=-12 is y =-2x+7.
What does equation of parallel lines mean?Parallel lines are those that never intersect. As a result, two parallel lines must have the same slope but different intercepts (if they had the same intercepts, they would be identical lines).
The equation of the line is 6x+3y=-12.
6x+3y=-12
3y =-12-6x
y = -2x-4
The slope of this line is -2.
Because parallel lines have the same slope, the new line will also have a slope of -2.
You now have a point (5,-3) and a slope; thus, use the Point-Slope form to solve the equation of a line.
y-y₁= m(x-x₁)
y+3 = -2(x -5)
y+3 = -2x+10
y =-2x+7
The equation of a line passing through the point (5,-3) and parallel to 6x+3y=-12 is y =-2x+7.
To know more about equation of parallel lines, visit:
https://brainly.com/question/402319
#SPJ9
Describe a strategy to visualize and calculate=20% off
40.
Answers
Answer:
32
Step-by-step explanation:
First you're going to change 20% to a decimal which would be 0.20
Next, multiply .20 by 40
You should get 8
Subtract 8 from 40
You're answer is 32
y=2x^(2)-3x+4 determine whether the equation defines y as a function of x
Answers
Yes, the given equation y = 2x² - 3x + 4 defines the variable y as a function of x.
What is a quadratic equation?A quadratic equation is a polynomial with a degree of 2 or the maximum power of the variable is 2 in quadratic equations. It has two solutions as its maximum power is 2.
The quadratic equation y = 2x² - 3x + 4 is showing y as the function of the variable x. The graph of the equation is attached with the answer below. in which the latex is at ( 0.75, 2.875).
Therefore, the given equation y = 2x² - 3x + 4 defines the variable y as a function of x.
To know more about quadratic equations follow
https://brainly.com/question/1214333
#SPJ2
Can someone help me find the value of x

Answers
Answer: 4
Step-by-step explanation:
Use the triangle to the right to find the measure of the side the two triangles share. That side is 8.06 roughly and squared it’s 65. I used the 65 to solve for b in a^2 + b^2 = c^2
65 + b^2 = 81
b^2 = 16
b = 4
Answer the following: (10 points) a. Find the area to the right of z= -1 for the standard normal distribution. b. First year college graduates are known to have normally distributed annual salaries wi
Answers
The area to the right of z = -1 for the standard normal distribution is approximately 0.8413.
a. To find the area to the right of z = -1 for the standard normal distribution, we need to calculate the cumulative probability using the standard normal distribution table or a statistical calculator.
From the standard normal distribution table, the area to the left of z = -1 is 0.1587. Since we want the area to the right of z = -1, we subtract the left area from 1:
Area to the right of z = -1 = 1 - 0.1587 = 0.8413
Therefore, the area to the right of z = -1 for the standard normal distribution is approximately 0.8413.
b. To answer this question, we would need additional information about the mean and standard deviation of the annual salaries for first-year college graduates. Without this information, we cannot calculate specific probabilities or make any statistical inferences.
If we are provided with the mean (μ) and standard deviation (σ) of the annual salaries for first-year college graduates, we could use the properties of the normal distribution to calculate probabilities or make statistical conclusions. Please provide the necessary information, and I would be happy to assist you further.
Learn more about area here
https://brainly.com/question/25292087
#SPJ11
James lives in san francisco and works in mountain view. in the morning, he has 333 transportation options (bus, cab, or train) to work, and in the evening he has the same 333 choices for his trip home.
Answers
The probability that James will take the same mode of transportation twice is 1/9.
To find the probability that James will take the same mode of transportation twice, we need to calculate the probability of each individual transportation option and then multiply them together.
In the morning, James has 3 transportation options: bus, cab, or train. Since he randomly chooses his ride, the probability of selecting any particular option is 1 out of 3 (assuming all options are equally likely).
Therefore, the probability of James selecting the same transportation mode in the morning and evening is 1/3.
Hence, the probability that James will take the same mode of transportation twice is 1/3 multiplied by 1/3:
P(same mode of transportation twice) = 1/3 * 1/3 = 1/9.
Therefore, the probability that James will take the same mode of transportation twice is 1/9.
To know more about probability:
https://brainly.com/question/31828911
#SPJ4
which type of armored cable is listed under ul 4, which is a prescriptive standard, with permitted conductor sizes of 14 awg through 1 awg only?
Answers
The type of armored cable listed under UL 4 with permitted conductor sizes of 14 AWG through 1 AWG only is Type AC Cable.
Type AC Cable is also known as armored cable or BX cable, and it is a type of electrical wiring that consists of two or more insulated conductors that are wrapped in a flexible metal sheath. The metal sheath provides protection against physical damage and also serves as a grounding conductor.
UL 4 is a standard for Armored Cable and it covers various types of armored cables, including Type AC cable. UL 4 specifies the construction, performance, and testing requirements for armored cables. It also includes requirements for the thickness and composition of the metal sheath, as well as the thickness and type of insulation on the conductors.
In summary, Type AC Cable is the type of armored cable that is listed under UL 4 and has permitted conductor sizes of 14 AWG through 1 AWG only.
To learn more about armored cable please click on below link.
https://brainly.com/question/30579494
#SPJ4
Which value is equivalent to 93.982
ОА 911
o
B
924
O c 8111
c

Answers
Help pls. HJ is an altitude of triangle FGH. M

Answers
stella and zeke have 26$ left for a cab fare home. the cab far is 4$ per mile plus 2$ fixed charge, what is the maximum number of miles they will be able to travel in the cab
Answers
Answer:
6miles
Step-by-step explanation:
They can go 6 miles because 26-2=24 24/6=4 4x6=24 so they can go 6 miles
Answer:
6 miles is the maximum amount they can afford
minus 2 from 26
2-26=24
then divide the total amount by 4
24/4= 6
The figure shows two lines cut by transversal.wich statement correctly explains why the two lines are parallel

Answers
Answer:
D
Step-by-step explanation:
This is because the angle are corresponding which mean they are on the same side and are the same number
Hope this Helped
Write an equation to model the given scenario, then solve:
Each year the local country club sponsors a tennis tournament. Play starts with 128 participants. During each
round, half of the players are eliminated. How many players remain after 5 rounds?
Answers
Given:
Initial number of participants = 128
During each round, half of the players are eliminated.
To find:
The number of players remain after 5 rounds.
Solution:
It is given that, the initial number of participants is 128 and during each round, half of the players are eliminated.
If half of the players are eliminated, then half of the players are remained.
So, the initial value is 128 and the decay factor is \(\dfrac{1}{2}\).
The general exponential decay model is:
\(y=a(b)^x\)
Where, a is the initial value and b is the decay factor.
Putting \(a=128\) and \(b=\dfrac{1}{2}\) in the above model, we get
\(y=128\left(\dfrac{1}{2}\right)^x\)
Here, y is the number of remaining players after x rounds.
Substituting \(x=5\), we get
\(y=128\left(\dfrac{1}{2}\right)^5\)
\(y=128\left(\dfrac{1}{32}\right)\)
\(y=4\)
Therefore, the required model is \(y=128\left(\dfrac{1}{2}\right)^x\) and the number of players remain after 5 rounds is 4.
a naturalist relocated 12 wild bears in 6 months. the naturalist relocated the same number of wilde bears each month how many wild bears did the naturalist relocate per month HELP SUPER URGENT
Answers
The number of wild bears the naturalist can relocate per month is 2 wild bears.
Number of wild bears relocated by the naturalist = 12 wild bears
Time taken by the naturalist to relocate these wild bears = 6 months
Thus the number of bears the naturalist can relocate in 1 month can be found out by using unitary method
This implies that the number of bears relocated by the naturalist in 1 month or per month = 12 / 6 = 2 wild bears
Thus the number of wild bears the naturalist can relocate per month is 2 wild bears .
To know more about unitary method or related problems you may visit the link which is mentioned below:
https://brainly.com/question/23423168
#SPJ1
Taylor is decorating for a party. She cuts 5 equal-length streamers from a strip of yellow paper that is 9 feet long. How long is each streamer in fraction form?
Answers
Answer: 1 4/5 feet
Step-by-step explanation:
Length of the strip of yellow paper = 9 feet.
Number of streamers that were cut = 5
Length of each streamer will then be:
= Length of the strip of yellow paper = 9 feet / Number of streamers that were cut
= 9 feet / 5
= 1 4/5 feet
PLEASE HELP ME!!!!
Given that f(x)=x+2 and g(x)=3x^2-1. What is (fg)(x)?
Answer: ???
PLEASE EXPLAIN YOUR REASONING!!
Answers
Done!
Which descriptions can describe more than one triangle? Select two options.
• side lengths of 6 ft, 8 ft, and 10 ft
0 angle measurements of 35°, 35°, and 110°
O angle measurements of 30°, 40°, and 50°
O angle measurements of 40°,
60°, and 80°
side lengths
of 4 cm, 6 cm, and 9 cm
Answers
The descriptions that can describe more than one triangle are
angle measurements of 35, 35, and 110°angle measurements of 40°, 60°, and 80°This is further explained below.
What is an angle?Generally, An angle is a figure produced in Euclidean geometry by two rays, which are referred to as the sides of the angle, and which have a common endpoint, which is referred to as the vertex of the angle. The plane that includes two rays will always contain the angles that are generated by the beams. Another way that angles are created is when two planes cross with one another. These particular angles are referred to as dihedral angles.
In conclusion, Measurements of 40 degrees, 60 degrees, and 80 degrees in relation to one another may define more than one triangle.
Read more about angle
https://brainly.com/question/13954458
#SPJ1
The first three cards dealt from a
well-shuffled deck of cards are spades. What is the probability that the next card dealt will be a spade?
Answers
666 views
Related Questions (More Answers Below)
Given AHAN = AJMS. If mZH = (3x + 22), mZA== (3x+22)", m_A = (2x+5)°, and m2J = (5x – 16)°,determine mZM.

Answers
Here is a speed-time graph. Speed (m/s) Time (t seconds)
a) Work out an estimate of the gradient of the graph at t = 2
Note: you must show how you use the graph to reach your answer.
b) What does the area under the graph represent?
Answers
Answer:
(a) - Refer to the step-by-step explanation.
(b) - Displacement of the object.
Step-by-step explanation:
To estimate the gradient of the graph at t = 2, we need to look at the slope of the line at that specific point. The gradient represents the rate of change of speed with respect to time.
Part (a) - Estimate of the gradient at t = 2:
To find an estimate of the gradient at t = 2, we can draw a tangent line to the curve at that point and determine its slope. If you could provide the specific values of speed (m/s) at different times around t = 2 (e.g., the speeds at t = 1.9 and t = 2.1), we can calculate the slope using the formula:
Slope = (Change in speed) / (Change in time).
With the additional information, we can proceed to estimate the gradient at t = 2.
Part (b) - The area under the graph represents the displacement or distance traveled.
The area under the speed-time graph corresponds to the distance or displacement traveled by the object. Since speed is the rate of change of distance, the area under the graph gives us the total distance covered during the given time interval. To calculate the area under the graph, you can divide it into individual shapes (rectangles, triangles, etc.) or use integrals and find their respective areas. Then, summing up these areas will give you the total distance traveled.
Please help with this question!!! It’s rlly simple!

Answers
Answer:
D. Multiply the second equation by 5
The best answer would have been to multiply the first equation by 1
I hope it helps