Answers
Related Questions
The chart below represents the steps in the process of a bill becoming a law. Use the chart to answer the following question.
The image represents the process of a bill becoming a law. It shows a set of parallel lines that merge, then split into two, and then merge again. Moving left to right, the top line has boxes labeled: A, C, E, G, and H. The bottom line has boxes labeled: B, D, F, and I. Boxes A and B, C and D, E and F, H and I, are paired. G is the only box on the top line without a corresponding box on the bottom line. Continuing to move from left to right, the two lines merge into one and have one box labeled J. Then the lines separate into two parallel lines again. The top line is labeled with box K and the bottom line is labeled with box L. The two parallel lines continue to the right where they again merge into one line, with an arrow pointing to a final box labeled M.
© 2011 FLVS
Which section of this chart represents the point where a bill is first debated in subcommittees?
A and B
H and I
C and D
K and L
Answers
Based on the description provided, the section of the chart that represents the point where a bill is first debated in subcommittees is: C and D
How to explain the informationIn the given chart, the parallel lines represent the progression of a bill through various stages in the legislative process. The boxes on the top line represent one set of actions or steps, while the boxes on the bottom line represent another set of actions or steps.
Moving from left to right on the chart, the boxes A and B are paired, representing a particular stage in the process. Similarly, the boxes C and D are paired, indicating another stage in the process.
In the context of the question, the stage where a bill is first debated in subcommittees is represented by the boxes C and D.
Learn more about chart on
https://brainly.com/question/25032284
#SPJ1
An octagon is a polygon with eight sides. Which of the following
this definition as a biconditional statement?
O If a polygon has eight sides, then it is an octagon
O A polygon is an octagon if and only if it has eight sides.
If a polygon is an octagon, then it has eight sides.
Answers
Answer:
The second answer option:
"A polygon is an octagon if and only if it has eight sides."
Step-by-step explanation:
A biconditional statement needs to have a conditional statement and also its reverse. This is in general happening in a case of a statement with the "If-and-only-if" form.
helpppp me pleassse its one tiny easy little question I give brainliest !!! ^^ I would really appreciate it <3
Answers
Answer:
where's the question?
a certain washing machine uses 29 gallons of water for each load of laundry washed. How many gallons of water would the washing machine use for 156 loads of laundry?
Answers
Answer:156
Step-by-step explanation:
The National Assessment of Educational Progress (NAEP) includes a mathematics test for eighth‑grade students. Scores on the test range from 0 to 500. Demonstrating the ability to use the mean to solve a problem is an example of the skills and knowledge associated with performance at the Basic level. An example of the knowledge and skills associated with the Proficient level is being able to read and interpret a stem‑and‑leaf plot.
In 2019, 147,400 eighth‑graders were in the NAEP sample for the mathematics test. The mean mathematics score was Xbar=282. We want to estimate the mean score in the population of all eighth‑graders. Consider the NAEP sample as an SRS from a Normal population with standard deviation =40.
If we take many samples, the sample mean Xbar varies from sample to sample according to a Normal distribution with mean equal to the unknown mean score in the population. What is the standard deviation of this sampling distribution?
Give your answer to four decimal places.
Answers
The standard deviation of the sampling distribution is approximately 0.3292.
What is central limit theorem?The behaviour of the sampling distribution of the mean is described by the central limit theorem, a key conclusion in statistics. It asserts that regardless of how the population distribution is shaped, if a random sample of size n is taken from a population with mean and standard deviation, the distribution of sample means will tend towards a normal distribution as n increases.
Because it enables us to utilise the normal distribution to draw conclusions about the population mean based on sample means, the central limit theorem has significant practical ramifications. Additionally, it offers a foundation for confidence interval estimation and statistical hypothesis testing.
The standard deviation is given by the formula:
SD = σ/√(n)
Now, substituting the value of σ = 40, n = 147,400 we have:
SD = σ/√(n) = 40/√(147400) ≈ 0.3292
Hence, the standard deviation of the sampling distribution is approximately 0.3292.
Learn more about central limit theorem here:
https://brainly.com/question/18403552
#SPJ1
g the mean value of land and buildings per acre from a sample of farms is $1300 with a standard deviation of $200. the data set has a bell shaped distribution. assume the number of farms in a sample is 80
Answers
With the empirical rule, we can estimate that the number of farms in the sample whose land and building values per acre are between $1100 and $1500 is approximately 50 farms.
The empirical rule (also known as the 68-95-99.7 rule) states that for data sets with a bell-shaped distribution:
68% of the data falls within one standard deviation of the mean.
95% of the data falls within two standard deviations of the mean.
99.7% of the data falls within three standard deviations of the mean.
Using this rule, we can estimate the number of farms whose land and building values per acre are between $1100 and $1500 as follows:
The mean value of land and buildings per acre from the sample of farms is $1300, and the standard deviation is $200.
$1100 is 1.5 standard deviations below the mean:
($1100 - $1300) / $200 = -1.0.
$1500 is 1 standard deviation above the mean:
($1500 - $1300) / $200 = 1.0.
Therefore, we can estimate that approximately:
68% of the farms in the sample have land and building values per acre between $1100 and $1500 plus or minus one standard deviation of $200. This is equivalent to approximately 50 farms, which is 68% of the sample size of 74 farms.
95% of the farms in the sample have land and building values per acre between $900 and $1700 plus or minus two standard deviations of $200. This is equivalent to approximately 70 farms, which is 95% of the sample size of 74 farms.
99.7% of the farms in the sample have land and building values per acre between $700 and $1900 plus or minus three standard deviations of $200. This is equivalent to approximately 73 farms, which is almost the entire sample size of 74 farms.
To learn more about Empirical rule :
https://brainly.com/question/28873888
#SPJ4
Note: The full question is:-
The mean value of land and buildings per acre from a sample of farms is $1300, with a standard deviation of $200. The data set has a bell-shaped distribution. Assume the number of farms in the sample is 74. Use the empirical rule to estimate the number of farms whose land and building values per acre are between $1100 and $1500.
A= 25 ft
B = 45 ft
A new arboretum was designed to contain two circular gardens. Garden A has a diameter of 25
ft and Garden B has a diameter of 45 ft.
a.
If the gardener wants to outline the gardens in edging, how many feet will be needed to
outline the smaller garden? (Express as an exact answer in terms of .)
Formula:
Answers
The perimeter of smaller circle is 78.5 ft
What is area?
Area is that the amount that expresses the extent of a vicinity on the plane or on a semicircular surface. space|the world|the realm} of a plane region or plane area refers to the world of a form or planate plate, whereas area refers to the world of associate degree open surface or the boundary of a three-dimensional object.
Main Body:
A new arboretum was designed to contain two circular gardens. Garden A has a diameter of 25 ft and Garden B has a diameter of 45 ft.
outline the smaller garden means circumference of the circle.
Perimeter of circle is 2πr.
diameter = 25 ft
radius = 25/2 = 12.5 ft
Radius = 2π *12.5
= 25 π
= 25*3.14
= 78.5 ft
Hence the perimeter of circle is 78.5 ft
to know more perimeter , visit :
https://brainly.com/question/397857
#SPJ1
NO LINKS!! Please assist me with this problem Part 1m

Answers
Answer:
(x + 8)² + (y - 8)² = 64=======================
Given ConditionsTangent to x-axis,Tangent to y-axis,In the second quadrant,Radius is 8 units.SolutionEquation of circle:
(x - h)² + (y - k)² = r², where (h, k) is center and r - radiusThe center is the radius long distance from the x- axis to left and y-axis up same distance, this makes it in the second quadrant.
So the coordinates of the center are:
x = - 8, y = 8The equation is:
(x - (-8))² + (y - 8)² = 8²(x + 8)² + (y - 8)² = 64
Answer:
\((x+8)^2+(y-8)^2=64\)
Step-by-step explanation:
Required conditions:
Tangent to both axes.Center in the second quadrant.Radius = 8 units.If the circle is tangent to both axes, its center will be the same distance from both axes. That distance is its radius.
If the center of the circle is in quadrant II, the center will have a negative x-value and a positive y-value → (-x, y).
Therefore, the coordinates of the center will be (0-r, 0+r) where r is the radius.
If the radius is 8 units, then the center is (-8, 8).
\(\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Substitute the found center and given radius into the formula to create an equation for the circle that satisfies the given conditions:
\(\implies (x-(-8))^2+(y-8)^2=8^2\)
\(\implies (x+8)^2+(y-8)^2=64\)

How can the graph of f(x) = 35x be transformed to represent the function g(x) = 35x – 3?
Translate the graph of f(x) - 3 units.
The point is on the graph of g(x).

Answers
Answer: Down | ( 8, -1 )
Step-by-step explanation:
Did the assignment
What is the answer to this question
Answers
Answer:
Excuse me, I believe you forgot to put your questio! To get the desired answer, I highly recommend to oost another question!
Have a great day!
Yours Truely, TheAnimeCatUwU
Step-by-step explanation:
-6z+(-5.5) + 3.5z + 5y - 2.5?
Answers
Answer:
-3.5z - 8 + 5y
Step-by-step explanation:
simplify -6z + -5.5 + 3.5z + 5y - 2.5
− 25z+5y−8
DIFFERENTIATE W.R.T. Z
−2.5
Five different awards are to be given to three students. Each student will receive at least one award. In how many different ways can the awards be distributed?
Answers
Answer:
A) 120
Step-by-step explanation:
A factorial is represented with an !
Ex: 7! = 7*6*5*4*3*2*1
In this case, we would use 5! which equals 120.
120 should be your answer.
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
Answers
Answer:
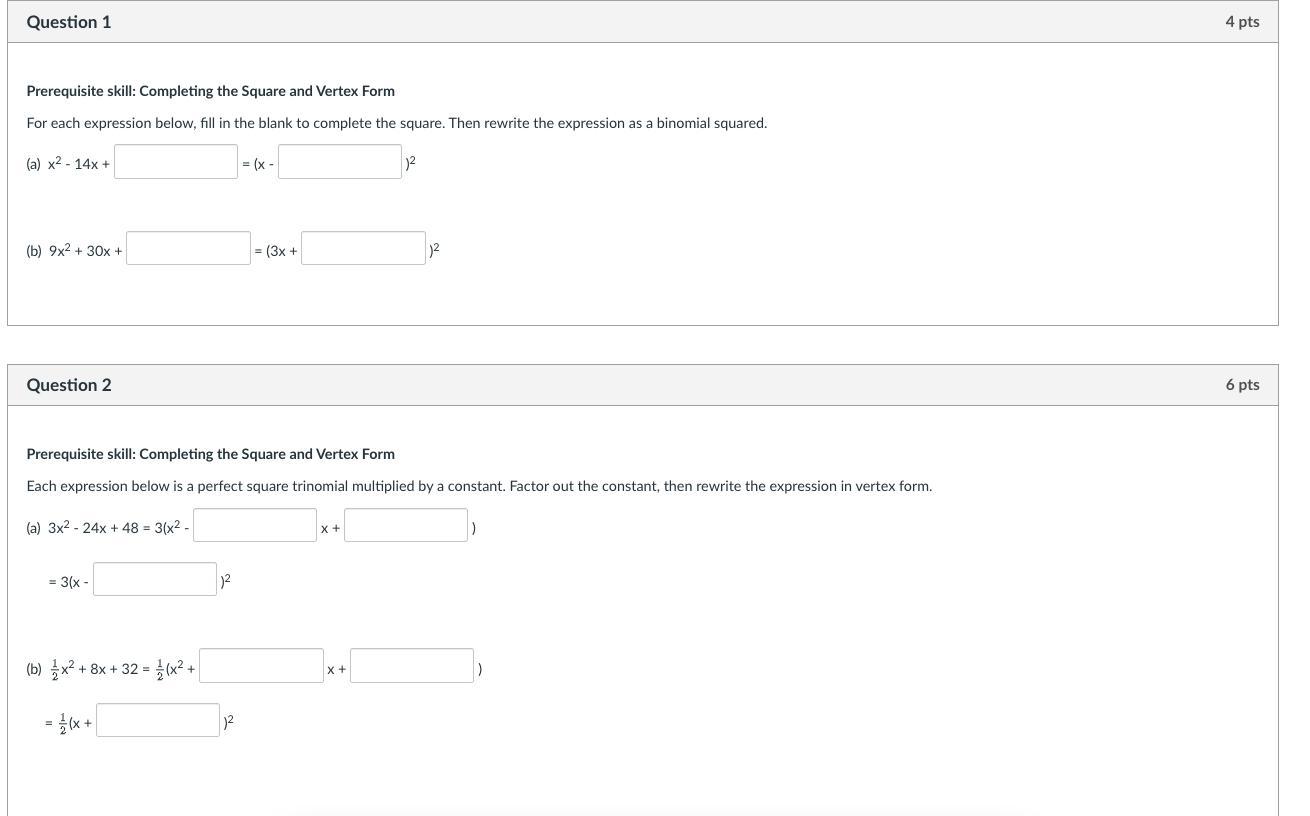
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Solve the system of equations below by graphing both equations with a pencil and paper. What is the solution? 3x + 4y = 38 5x - 5y = 30
Answers
The solution of given system of equations is (10, 4).
What is a linear system of equations?A system of linear equations consists of two or more equations made up of two or more variables such that all equations in the system are considered simultaneously. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.
The given system of equations are 3x+4y=38 -----(I) and 5x-5y=30 -------(II)
x-y=6 -------(III)
x=6+y
Substitute x=6+y in equation (I), we get
3(6+y)+4y=38
18+1y+4y=38
5y=20
y=4
Substitute y=4 in equation (III), we get
x=10
So, the solution is (10, 4)
Therefore, the solution of given system of equations is (10, 4).
To learn more about the linear system of an equations visit:
https://brainly.com/question/27664510.
#SPJ1

Given: m || n
What is the value of x?
x =

Answers
Explanation: 46 degrees is a vertical angle to the equation, and when you plus in 8 you get 48, then subtract 2 you end up with 46 degrees. Hope this helps.
Which number is a solution of the inequality: B > 2.1
A: -8
B: -12
C:5
D: 1
Answers
Answer:
C. 5 is solution of the inequality: B>2.1
What is the slope of the line in this graph?
A) -5/3
B) -3/5
C) 3/5
D) 5/3

Answers
Answer:
A)
Step-by-step explanation:
rise/run
down 5, left 3
Multiply.
(2x+6)²
NEED ANSWER ASAPP
Answers
Answer:
4x² + 24x + 36
Step-by-step explanation:
(2x + 6)² = (2x + 6)(2x + 6) = 4x² + 12x + 12x + 36 = 4x² + 24x + 36
Find the amount of tax and the tax rate. Round to two decimal places.
Cost of item: $71
Selling price: $86.45
Tax amount: $
Tax rate: %
Answers
well, the tax amount is simple, it was $71 and it went up to $86.45, that's a 15.45 difference, so that IS the tax amount.
now, if we take 71(origin amount) to be the 100%, what's 15.45 off of it in percentage?
\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 71 & 100\\ 15.45& x \end{array} \implies \cfrac{71}{15.45}~~=~~\cfrac{100}{x} \\\\\\ 71x=1545\implies x=\cfrac{1545}{71}\implies x\approx 21.76\)
I need Help please!!!

Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
HELLPPPP PLEASE
I WILLL MARK YOU BRILL

Answers
Answer:
13
Step-by-step explanation:
71-6=65
65/5=13
therefore the answer is 13
5d + 6 = 71
5d = 71 - 6
5d = 65
d = 65/5
d = 13
6. How many cans each 1.5 litres in capacity can be filled from a tank containing 63 litres of water?
Answers
42 cans each 1.5 litres in capacity can be filled from a tank containing 63 litres of water.
Given, the capacity of each can is 1.5 litres and the tank holding 63 litres of water. We have to find the number of cans that can be filled from the tank containing 63 litres of water.
Let x number of cans can be filled from the tank containing 63 litres of water having each 1.5 litres in capacity, we have
x = 63/1.5
x = 630/15
x = 42
∴ The required answer is 42.
Hence, 42 cans each 1.5 litres in capacity can be filled from a tank containing 63 litres of water.
Learn more in depth about capacity at https://brainly.com/question/17303238
#SPJ9
Which of the following represents the series? –13 + (–7) + (–1) + 5 + 11
Answers
Answer:
Adding +6 in turn
Step-by-step explanation:
-13+6=(-7)
(-7)+6=(-1)
(-1)+6=5
5+6=11
11+6=17
17+6=23
23+6=29
29+6=35
........... And so on
if it helped uh please mark me a brainliest :))What is the measure of the angle indicated?
ANSWER CHOICES
120 Degrees
155 Degrees
85 Degrees
60 Degrees

Answers
A dairy needs 258 gallons of milk containing 7% butterfat how many gallons each of milk containing 8% butterfat and milk containing 2% butterfat must be used to obtain the desired 258 gallons
Answers
Let's assume x gallons of milk containing 8% butterfat and y gallons of milk containing 2% butterfat are used.
The total amount of milk is x + y gallons, and we want it to be equal to 258 gallons.
To determine the amount of butterfat in the mixture, we can multiply the volume of each type of milk by its respective butterfat percentage and sum them up.
For milk containing 8% butterfat, the amount of butterfat is 0.08x (8% is equivalent to 0.08 as a decimal).
For milk containing 2% butterfat, the amount of butterfat is 0.02y (2% is equivalent to 0.02 as a decimal).
Since we want the final mixture to contain 7% butterfat, we can set up the following equation:
0.08x + 0.02y = 0.07(258)
Simplifying the equation, we have:
0.08x + 0.02y = 18.06
To solve for x and y, we need another equation. Since the total amount of milk is x + y = 258, we can rearrange it to y = 258 - x.
Substituting this value into the equation above, we get:
0.08x + 0.02(258 - x) = 18.06
Solving this equation will give us the values of x and y, which represent the gallons of milk containing 8% butterfat and 2% butterfat, respectively, needed to obtain the desired 258 gallons.
For such more question on gallons
https://brainly.com/question/28274339
#SPJ8
Find the domain and range of the function f(x) = sqrt(2 - x - x ^ 2) .
Answers
Answer:
See belowStep-by-step explanation:
Given function:
\(f(x) = \sqrt{2 - x - x ^ 2}\)As any square root function, its range is all non-negative numbers:
f(x) ≥ 0 or f(x) ∈ [0, +∞)The domain the x values when the expression under root is non-negative:
2 - x - x² ≥ 0x² + x - 2 ≤ 0(x + 2)(x - 1) ≤ 0- 2 ≤ x ≤ 1or
x∈ [-2, 1]ASAPP PLEAASSEE!!!
Nathan deposits $940 every 2 months into his daughter's RESP. If the account earns 3.99% / annual, compound quarterly, how much will be in the account after 25 years?
Answers
There will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
To calculate the amount in Nathan's daughter's RESP after 25 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount (amount in the account after 25 years)
P = Principal amount (amount deposited every 2 months)
r = Annual interest rate (in decimal form)
n = Number of times the interest is compounded per year
t = Number of years
In this case, Nathan deposits $940 every 2 months, so the principal amount (P) is $940. The annual interest rate (r) is 3.99% or 0.0399 in decimal form. Since the interest is compounded quarterly, the compounding frequency (n) is 4. The number of years (t) is 25.
Since Nathan deposits every 2 months, we need to calculate the total number of deposits made over 25 years. There are 12 months in a year, so in 25 years, there will be 25 * 12 = 300 months. However, since Nathan deposits every 2 months, the number of deposits (m) is 300 / 2 = 150.
Now, we can substitute these values into the formula:
A = 940(1 + 0.0399/4)^(4*25)
Calculating the exponent first:
(1 + 0.0399/4)^(4*25) ≈ 2.703236
Now, substituting the calculated exponent and the number of deposits into the formula:
A = 940 * 2.703236 * 150 ≈ $594,311.34
Therefore, there will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
It's important to note that this calculation assumes Nathan makes the same $940 deposit every 2 months consistently over the 25-year period and does not make any withdrawals from the account during that time. Additionally, the actual amount may vary slightly due to rounding and any potential changes in interest rates over the years.
For more such questions on compounded visit:
https://brainly.com/question/24274034
#SPJ8
The volume of the prism below is 180in3. What is the value of x?

Answers
To find the volume of a cuboid, you do the length x width x height
3 x 5 x ´x’ = 180
Simplify:
15 x ´x’ = 180
To find ´x’, divide 180 by 15
180 / 15 = 12
x = 12
When x > 0 and y > 0, what expression is equivalent to √180x^9y^16 in simplest form?
Answers
Answer:
\(6x^4y^8\sqrt{5x}\)
Step-by-step explanation:
\(\textsf{When $x > 0$ and $y > 0$, we want to find the expression that is equivalent to}\) \(\sqrt{180x^9y^{16}}.\)
\(\textsf{First, apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{180}\sqrt{x^9}\sqrt{y^{16}}\)
\(\textsf{Rewrite $x^9$ as $x^{8+1}$:}\)
\(\sqrt{180}\sqrt{x^{(8+1)}}\sqrt{y^{16}}\)
\(\textsf{Apply the exponent rule:} \quad a^{b+c}=a^b \cdot a^c\)
\(\sqrt{180}\sqrt{x^{8}\cdot x^1}\sqrt{y^{16}}\)
\(\sqrt{180}\sqrt{x^{8}}\sqrt{x}\sqrt{y^{16}}\)
\(\textsf{Apply\:the\:radical\:rule:\:}\sqrt[n]{a^m}=a^{\frac{m}{n}},\:\quad a\geq 0\)
\(\sqrt{180}\;x^{\frac{8}{2}}\sqrt{x}\;y^{\frac{16}{2}}\)
\(\sqrt{180}\;x^4\sqrt{x}\;y^8\)
\(\sqrt{180}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Rewrite $180$ as $(6^2 \cdot 5)$:}\)
\(\sqrt{6^2 \cdot 5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{6^2} \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a^2}=a, \quad a \geq 0\)
\(6 \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a}\sqrt{b}=\sqrt{ab}\)
\(6 \sqrt{5x}\;x^4\;y^8\)
\(\textsf{Rearrange:}\)
\(6x^4y^8\sqrt{5x}\)
\(\textsf{Therefore, when $x > 0$ and $y > 0$, the expression that is equivalent to}\)
\(\sqrt{180x^9y^{16}}\;\textsf{is}\;\;\boxed{6x^4y^8\sqrt{5x}}\:.\)
Help me with this pls!!

Answers
Answer:
5 3/4 hours
Step-by-step explanation:
They drove 3 1/2 hours then 2 1/4 hours. We need to find the total of these to find how long this part of the trip was
(3 + 1/2) + (2 + 1/4) = 5 + 1/2 + 1/4
For 1/2, we can multiply both the numerator and denominator by 2 to get
1/2 = 2/4
Substituting that in, we get
5 + 2/4 + 1/4
= 5 + 3/4 hours
