Which is the minimum or maximum value of the given function? A parabola declines through (negative 5, negative 2), (negative 3, negative 4) and rises through (negative 2, negative 3 point 5), (negative 1, negative 2), (0, 0), (0 point 5, 2) and (1, 4) on the x y coordinate plane. A. The function has a minimum value of -4. B. The function has a maximum value of -4. C. The function has a minimum value of -3. D. The function has a maximum value of -3.
Answers
The parabola function has a minimum value of -4.
How to determine the maximum or the minimum?The given parameters are:
Declines through (-5,-2), (-3,-4)Rises through (-2, -3), (-1, -2), (0, 0), (0, 2) and (1, 4)Because the parabola declines before it rises, it means that the function has a minimum
From the point of decline;
-4 is less than -2
Hence, the parabola function has a minimum value of -4.
Read more about parabola at:
https://brainly.com/question/1480401
#SPJ1
Related Questions
Find an equation or inequality that describes the following object. A ball with center (9,-9, -1) and radius 8. Choose the correct answer below. A. (X + 9)2 + (y - 9)2 + (z − 1)2 564 B. (X-9)2 + (y + 9)2 + ( + 1)2 = 64 C. (X-9)2 + (y + y + 9)2 + (x + 1)2 564 D. (X+9)2 + (y-9)2 + (2-1)2264
Answers
The equation \((x-9)^2 + (y + 9^2 + (z + 1)^2 = 64\) represents a ball with a center at (9, -9, -1) and a radius of 8. Therefore, correct option is B.
To find the equation or inequality that describes the given object, we need to consider the equation of a sphere in three-dimensional space. The general equation of a sphere with center (a, b, c) and radius r is:
\((x - a)^2 + (y - b)^2 + (z - c)^2 = r^2\)
In this case, the center of the ball is given as (9, -9, -1), and the radius is 8. Plugging these values into the equation, we have:
\((x - 9)^2 + (y + 9)^2 + (z + 1)^2 = 8^2\)
Simplifying the equation gives:
\((x - 9)^2 + (y + 9)^2 + (z + 1)^2 = 64\)
Therefore, the correct equation that describes the ball is B.
\((x-9)^2 + (y + 9)^2 + (z + 1)^2 = 64.\)
This equation can be used to determine if a given point lies inside or outside the ball. By substituting the coordinates of a point into the equation, we can compare the value to the radius squared (64) to determine the position of the point relative to the ball.
To know more about Equation, visit
https://brainly.com/question/29174899
#SPJ11
A church has 475 members of the congregation. 32% of the congregation are senior citizens and 24% are children. work out the number of members from the congregation who are neither
Answers
24% of 475 = 114
Remaining = 475-152-114=209 is the amount who are neither
Use this figure. Help me answer this please

Answers
f(x) = 3x + 5
g(x) = 4x² - 2
h(x) = x²-3x+1
Find f(x) + g(x) - h(x).
O 3x² + 6x + 2
-O 3x²+2
O 6x2² +6x-1
O 5x² +4
Answers
After solving the expression we get 3x² ₊ 6x ₊ 2 .
Given f(x) = 3x₊5
g(x) = 4x² ₋ 2
h(x) = x² ₋ 3x ₊ 1
f(x) ₊ g(x) ₋ h(x)
substitute the values.
3x ₊ 5 ₊ 4x² ₋ 2 ₋ (x² ₋ 3x ₊ 1)
4x² ₊ 3x ₊ 3 ₋ x² ₊ 3x ₋ 1
3x² ₊ 6x ₊ 2
hence we get 3x² ₊ 6x ₊ 2 .
Learn more about Functions here:
brainly.com/question/15602982
#SPJ9
(1-1) what proportion of a normal distribution is located in the tail beyond z = 1.00? (1) 0.1587
(2)-0.3413
(3)-0.1587
(4)0.8413
Answers
The proportion of a normal distribution located in the tail beyond z = 1.00 is 0.1587.
The normal distribution is a continuous probability distribution, and the area under its curve is 1.0. The normal distribution is symmetric with respect to the mean, which is zero, and has a bell-shaped curve. The tails of the normal distribution approach the horizontal axis, but they never meet it. The curve is entirely above the horizontal axis, and its total area equals 1.The standard normal distribution's curve, which is a normal distribution with a mean of 0 and a standard deviation of 1, has a total area of 1.0. Half of the total area is located on each side of the mean. Half of the area of the standard normal distribution is located in the right-hand tail beyond z=0. The area of the standard normal distribution located in the left-hand tail beyond z=0 is also half. Half of the tail area of the standard normal distribution beyond z=1.00 is located in the right-hand tail beyond z=0. The left-hand tail area beyond z= -1.00 is also half of the total area beyond z= -1.00. Therefore, the proportion of a normal distribution located in the tail beyond z = 1.00 is 0.1587.
Know more about normal distribution here:
https://brainly.com/question/32093921
#SPJ11
i got the first part but cant figure out the second, help would be appreciated

Answers
Answer:
see explanation
Step-by-step explanation:
look at the explanation& answer photo


Consider the system of equations
5x+3y=30
−5x−2y=−25
Part A: Solve the system. Show your work.
_______
Part B: Use the solution to your equation to find the value of x – y. Show your work.
x−y = _____
Answers
By solving the two equations, the values of x , y and x-y are found to be 1, 25/3 and -22/3 respectively.
Given two equations are;
5x+3y=30..........(1)
−5x−2y=−25.........(2)
Now , from (2)
−5x−2y=−25
⇒ 5x +2y = 25 (multiply both sides with '-' sign)
⇒ y = \(\frac{(25 -5x)}{2}\)
Solving the system;
substitute the above vale of y in eq (1)
5x + 3y = 30
⇒ 5x + 3 ( \(\frac{(25 -5x)}{2}\)) = 30
⇒ 5x + (\(\frac{(75 - 15x)}{2}\)) = 30
⇒ \(\frac{10x+75-15x}{2}\) = 30
⇒ -5x + 75 = 60
⇒ -5x = -5
⇒ x = 1
∴ x = 1
Now substitute the value of x in (1)
5x + 3y = 30
⇒ 5 × 1 + 3y = 30
⇒ 3y = 25
⇒ y = 25/3
∴ y = 25/3
Now using the value of x and y , we can find the value of x - y
x - y = 1 -25/3 = (3 - 25)/ 3 = -22/3
∴ x - y = -22/3
Learn more about solving equation here;
https://brainly.com/question/22688504
#SPJ1
Reduce this question to lowest terms 4/5 divided by 16/15
Answers
i found 3/4 but am not that sure if it's correct
If f(x)=3x-1 and g(x)=x+2, find (f+g)(x)

Answers
Answer:
4x+1
Step-by-step explanation:
Perform the indicated operations and simplify.
(x - 3y)² + 3(x + y)(x − 4y) + x(3x + 4y + 3)
Answers
Let's simplify the expression step by step: Expand the squared term:
(x - 3y)² = (x - 3y)(x - 3y) = x² - 6xy + 9y²
Expand the second term:
3(x + y)(x − 4y) = 3(x² - 4xy + xy - 4y²) = 3(x² - 3xy - 4y²)
Expand the third term:
x(3x + 4y + 3) = 3x² + 4xy + 3x
Now, let's combine all the expanded terms:
(x - 3y)² + 3(x + y)(x − 4y) + x(3x + 4y + 3)
= x² - 6xy + 9y² + 3(x² - 3xy - 4y²) + 3x² + 4xy + 3x
Combining like terms:
= x² + 3x² + 3x² - 6xy - 3xy + 4xy + 9y² - 4y² + 3x
= 7x² - 5xy + 5y² + 3x
The simplified form of the expression is 7x² - 5xy + 5y² + 3x.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
TRUE/FALSE. in a poisson distribution, the probability of success may vary from trial to trial.
Answers
The statement is false because in a Poisson distribution, the probability of success does not vary from trial to trial.
The Poisson distribution is a discrete probability distribution that describes the number of times an event occurs in a fixed time interval or spatial region, given the average rate of occurrence and assuming that the events are independent and random.
The Poisson distribution has only one parameter, λ, which represents the average rate of occurrence of the event.
The probability of observing k events in the interval is given by the Poisson probability mass function:
P(k) = (e^(-λ) * λ^k) / k!
where e is the base of the natural logarithm, and k is a non-negative integer.
The Poisson distribution assumes that the probability of observing an event at any given point in time or space is constant, and that the events are independent of each other.
To know more about Poisson distribution refer here:
https://brainly.com/question/30388228#
#SPJ11
For the standard normal random variable z, find z for each situation. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)'
a. The area to the left of z is 0.1827. z =
b. The area between −z and z is 0.9830. z =
c. The area between −z and z is 0.2148. z =
d. The area to the left of z is 0.9997. z =
e. The area to the right of z is 0.6847. z=
Answers
The z-values for the given situations are approximate:
a. The area to the left of z is 0.1827. z = -0.90
b. The area between −z and z is 0.9830. z = 2.17
c. The area between −z and z is 0.2148. z = 0.85
d. The area to the left of z is 0.9997. z = 3.49
e. The area to the right of z is 0.6847. z= -0.48
a. For an area of 0.1827 to the left of z, the corresponding z-value can be found using a standard normal distribution table or a statistical calculator. The z-value is approximately -0.90.
b. To find the z-value for an area between -z and z equal to 0.9830, we need to find the value that corresponds to (1 - 0.9830)/2 = 0.0085 in the upper tail of the standard normal distribution. Using the table or calculator, the z-value is approximately 2.17.
c. Similarly, for an area between -z and z equal to 0.2148, we find the value that corresponds to (1 - 0.2148)/2 = 0.3926 in the upper tail. The z-value is approximately 0.85.
d. For an area of 0.9997 to the left of z, we find the value that corresponds to 0.9997 in the upper tail. The z-value is approximately 3.49.
e. To find the z-value for an area to the right of z equal to 0.6847, we find the value that corresponds to 1 - 0.6847 = 0.3153 in the upper tail. The z-value is approximately -0.48.
In summary, the z-values for the given situations are approximate:
a. -0.90
b. 2.17
c. 0.85
d. 3.49
e. -0.48
These values can be used to determine the corresponding percentiles or probabilities for the standard normal distribution. The values are typically found using standard normal distribution tables or statistical calculators that provide the cumulative probability distribution function (CDF) for the standard normal distribution.
For more such answers on z-values
https://brainly.com/question/28000192
#SPJ8
Can someone help me with number 8 :(

Answers
Answer:
a1=5
d=9-5=4
a20=5+19×4=81
when 7 is added to 3 times a certain number, the result is 22"
Answers
Answer:
The answer would be 5!
Step-by-step explanation:
22-7= 15
15/3 = 5
You can plug the 5 back in to check your work like so:
5 x 3 = 15
15 + 7 = 22
How do you eliminate negative exponents?.
Answers
To eliminate negative exponents the base is inverted by taking its reciprocal, and the exponent then becomes positive.
Given:
Eliminating negative exponents:
Example:
1) \(x^{-5}\)
on reciprocal:
= 1/x^5
eliminated negative
2) \(x^{-7}y^{-4}\)
= x^-7*1/y^4
= 1/x^7y^4
Therefore To eliminate negative exponents the base is inverted by taking its reciprocal, and the exponent then becomes positive.
Learn more about the exponents here:
https://brainly.com/question/15993626
#SPJ4
Find values of m so that the function y xm is a solution of the given differential equation. x^2y''-7xy' 15y=0
Answers
If \(y=x^m\) is a solution to the ODE
\(x^2 y'' - 7xy' + 15y = 0\)
then substituting \(y\) and its derivatives
\(y' = mx^{m-1} \text{ and } y'' = m(m-1)x^{m-2}\)
gives
\(m(m-1)x^2x^{m-2} - 7mxx^{m-1} + 15x^m = 0\)
\(m(m-1)x^{m} - 7mx^{m} + 15x^m = 0\)
\((m(m-1) - 7m + 15)x^{m} = 0\)
We ignore the trivial case of \(y=x^m=0\). Solve for \(m\).
\(m(m-1) - 7m + 15 = 0\)
\(m^2 - 8m + 15 = 0\)
\((m - 3) (m - 5) = 0\)
\(\implies \boxed{m=3} \text{ or } \boxed{m=5}\)
Characterize the slope of the line in the graph.
A. Zero
B. Undefined
C. Negative
D. Positive
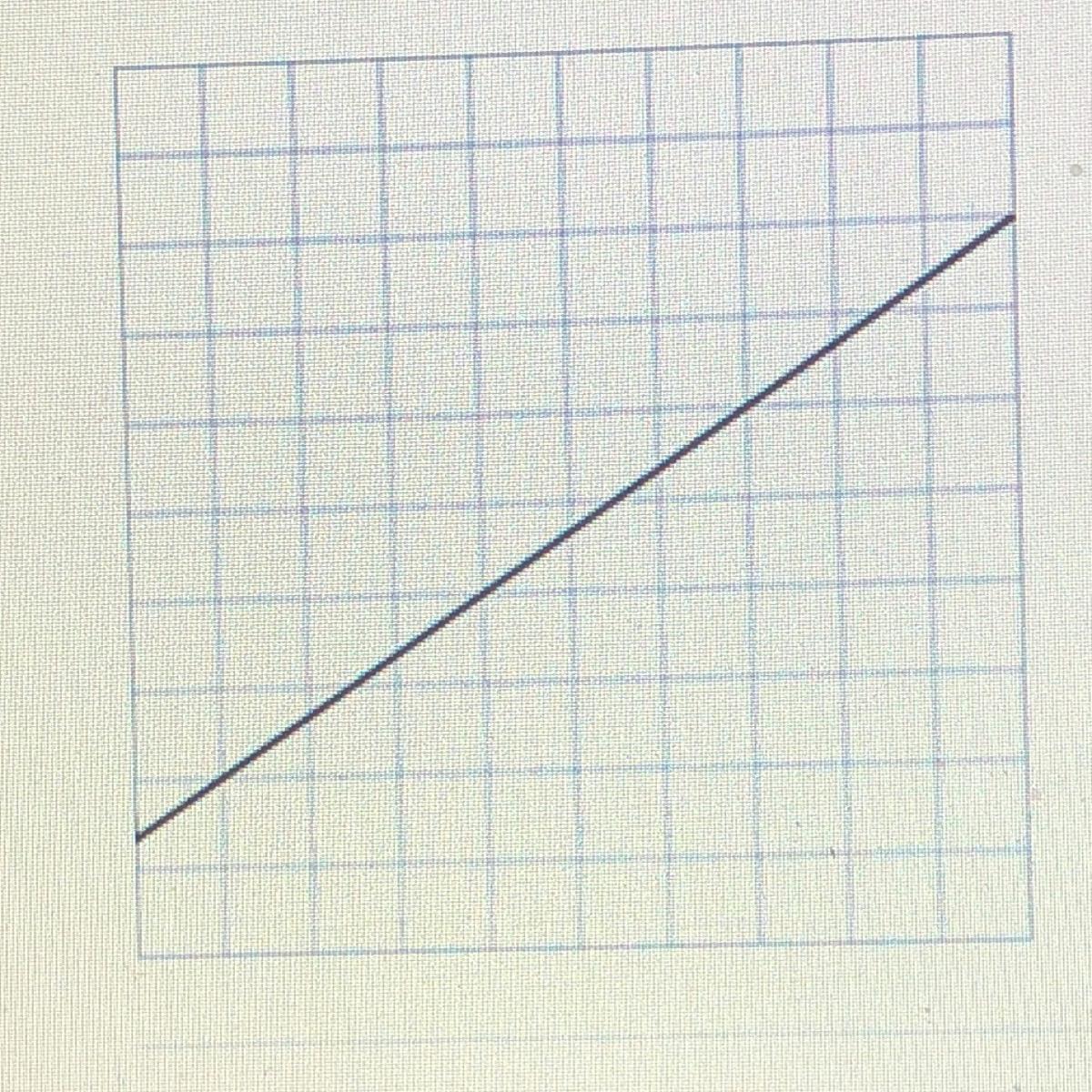
Answers
D.Positive
1. At dinner Mr. Murphy’s bill came out to $39.99 before tax and tip sales tax is 6% he wants to also have a 20% tip how much money will he end up spending altogether.
2. What’s 15% of 180
Answers
$39.99 / 100 = 0.399
0.399 x 126 = $50.39
Total = $50.39
2. 180 / 100 = 1.8 (1%)
X 15
= 27
Answer is 27.
By the way a quicker method would be to:
180 x 0.15 = 27
If you understand it.
If tori decides to make 200 chocolate chip cookies and no vanilla sprinkle cookies, which constraint would be binding?.
Answers
Oven hours are a binding constraint because Tori needs 0.04 x 200, or 8 hours, to manufacture 200 chocolate chips, and the same is true for the upper-level restriction.
Binding restrictions are those whose removal would lead to the largest advances in entrepreneurship and growth. Some locations are unbound. The dual value measures how much the objective function's value rises for each additional unit of the variable's value. A constraint's dual value only deviates from zero when it equals its bound.
This is a binding constraint, and during optimization, its value was pushed as close as possible to the bound. If your answer matches the Right-Hand Side (RHS) of the inequality, the constraint is BINDING. If your response does not match the RHS of the inequality, the constraint is NON-BINDING.
To read more about Binding Constraints, visit https://brainly.com/question/14582910
#SPJ4
Mikah and Gracie were running laps at the local gym. Mikah ran 1 and 4/8 laps, and Gracie ran 1 and 1/2 laps. Who ran a further distance?
Answers
Answer:
Trick question they both ran equal distance
Step-by-step explanation:
Gracies distand 1 and 1/2 is already in simplist form, but Mikahs distance 1 and 4/8 can be reduced.
More specifically the fration 4/8 can be reduced, finding the largest common multiple between 4 and 8 we find that 4 is the largest number that goes into both.
This results in the simplification of 1 and 4/8 to 1 and 1/2 which is the same as Gracies distance.
dan spent 40$ at thr grocery store. of this amount he spen 8$ on fruit. what percentgae of the total did he spend on fuit
Answers
The percentage of the total which he spend on fruits is 20 %.
He spent $40 in total and $8 on fruit,
therefore he spent $8/40 on fruit.
This number can be made simpler because both the numerator and denominator are even.
8/40 ÷ 8/8 = 1/5
This means that he spends a total of 20 % on fruits.
There is no dimension to percentages. As a result, it is known as a dimensionless number. When we say a number is 50% of anything, we mean that it is 50% of everything.
As in 0.6%, 0.25%, etc., percentages can also be expressed as decimals or fractions. The grades earned in any topic are calculated in terms of percentages in academics.
Ram, for instance, scored 78% in his final exam. This percentage is derived based on Ram's overall grade point average (GPA) across all disciplines.
To learn more about percentage
brainly.com/question/29306119
#SPJ4
Evaluate the function when x = -5.
f(x) = 2x + 7
answer:
Answers
Answer:
Step-by-step explanation:
Replace x with -5
2(-5)+7
-10+7
-3
Answer:
-3
Step-by-step explanation:
Evaluate 2 x + 7 where x = -5:
2 x + 7 = 7 - 5×2
Hint: | Multiply 2 and -5 together.
2 (-5) = -10:
-10 + 7
Hint: | Subtract 10 from 7.
7 - 10 = -3:
Answer: -3
a student on the 20 m line of a metric football field kicks a football at an angle of 53 with an initial velocity of 25 m/s find the time the football is in the air, what meter line the football lands on and the ball's maximum height
Answers
The time the football is in the air is approximately 4.07s and the football lands on or around the 81.23meter line. the ball's maximum height is approximately 20.33 meters.
How can we calculate the time of flight at an angle with a given initial velocity?
The time of flight can be calculated using the equation:
\(\frac{(2 * initial velocity * sin(angle))}{gravitational acceleration}\). The meter line the football lands on can be found by calculating the horizontal distance traveled using the equation (initial velocity * cos(angle) * time of flight). The maximum height can be determined using the formula \(\frac{ (initial velocity^2 * sin^2(angle)) }{(2 * gravitational acceleration)}\).
To find the time the football is in the air, the meter line it lands on, and the ball's maximum height, we can use the equations of motion for projectile motion.
1.Time of flight:
The time the football is in the air can be determined using the formula:
Time of flight = \(\frac{(2 * initial velocity * sin(angle))}{gravitational acceleration}\)
Given:
Initial velocity (u) = 25 m/s
Angle (θ) = 53°
Gravitational acceleration (g) = 9.8 m/s²
Time of flight =\(\frac{(2 * 25 * sin(53\°))}{9.8}\)
≈ 4.07 seconds
Therefore, the time the football is in the air is approximately 4.07 seconds.
2.Meter line the football lands on: To determine the meter line the football lands on, we need to calculate the horizontal distance traveled by the football.
Horizontal distance = initial velocity * cos(angle) * time of flight
Horizontal distance = 25 * cos(53°) * 4.07
≈ 61.23 meters
Since the student is on the 20-meter line, adding the horizontal distance to the starting position gives us:
Meter line the football lands on = 20 + 61.23 ≈ 81.23 meters
Therefore, the football lands on or around the 81.23-meter line.
3.Maximum height: The maximum height reached by the football can be found using the formula:
Maximum height = \(\frac{(initial velocity^2* sin^2(angle))}{ (2 * gravitational acceleration)}\)
Maximum height = \(\frac{(25^{2} * sin^2(53\°))}{(2 * 9.8)}\)
≈ 20.33 meters
To learn more about the time of flight from the given link
brainly.com/question/30337310
#SPJ4
list the 10 possible samples (without replacement) of size 2 that can be obtained from the population of five officials.
If a simple random sampling procedure is used to obtain a sample of two officials, what are the chances that it is the first sample on your list in part​ (a)? the second​sample? the tenth​ sample?
Answers
On solving the provided question, we can say that the random sampling is \(^5C_{2}\) = 4X5/ 2= 10
What is Random Sampling?A simple random sample may be 25 employees chosen at random from a firm with 250 workers. Since there are 250 of her employees in total, and each one has an equal probability of being chosen, the sample in this instance is random. The sampling technique of random sampling, also known as probabilistic sampling, enables the randomization of sample selection. It is crucial to keep in mind that populations as a whole are not always accurately represented by sampling. Sampling error is the term used to describe all variance.
population size, \(N = 5\)
sample size, \(n = 2\\\)
\(^5C_{2}\) = 4X5/ 2
= 10
To know more about Random Sampling visit:
https://brainly.com/question/12719656
#SPJ4
Alexander found the means to MAD ratio of 2 data sets to be 2. 1
What can he conclude Bout the distributions?
Answers
Alexander can conclude that the inconstancy (spread) of the information in one dataset is twice as much as the changeability of the information within the other dataset.
The mean absolute deviation (MAD) could be a degree of inconstancy that depicts the normal separation between each information point and the cruelty of the dataset. The bigger the Frantic esteem, the more spread out the information is. The proportion of the implies to MADs of two datasets can be utilized to compare their spread.
In this case, the proportion of implies to MADs is 2.1. This implies that the cruelty of one dataset is 2.1 times bigger than the Frantic of that dataset, whereas the cruelty of the other dataset is as if it were 1 times bigger than its Frantic. Hence, the dataset with the bigger proportion (2.1) encompasses a bigger spread (inconstancy) compared to the other dataset.
To learn about mean absolute deviation visit:
https://brainly.com/question/10528201
#SPJ4
Find the value of x. Then find the angle measures of the polygon.
Please help me as soon as possible, it would be great if you gave me an explanation!

Answers
For number 20:
Because a triangle is 180 degrees, we will equal all the angles we know to that. So, this is how we will write our equation:
Solve for x:
60 + x + 20 + 3x = 180
4x = 100
x = 20
Using 75, you can find the angle measure by plugging 75 where x is present in the angle measures. For example:
x = 20,
20 + 20 = 40
3(20) = 60
-
For number 21:
The shape shown is basically two triangles, so 180 x 2 is 360. Again, same procedure. Add all known angle measures and make an equation where they all equal 360.
Solve for x:
x-5+x+35+1.4x+x=360
x = 75
By isolating x, you should get an answer of 75. Now, plug that into each of the equations:
x = 75
75 + 35 = 110
75 - 5 = 70
1.4(75) = 105
help:(
Use the table of values to evaluate the expressions below. f(x) g(x) 4 7 6 9 7 3 5 4 1 8 0 1 3 5 8 0 2 6 9 2 08 1 2 6789SAW3 4 5 f(g(1)) = = g(f(5)) = f(f(9)) 9(g(3)) = = P 00
Answers
Using the table of values, we have:
f(1) = 7,
g(1) = 4,
and f(g(1)) = f(4) = 1. Thus, f(g(1)) = 1.
g(5) = 1,
g(5) = 8. Thus, g(f(5)) = g(7) = 4. Therefore, g(f(5)) = 4.
Since f(9) is not in the table of values, we cannot evaluate it directly. However, we can use f(8) = 2, f(2) = 6, and f(6) = 5 to find f(f(9)).
f(f(9)) = f(f(8)) = f(2) = 6. Thus, f(f(9)) = 6.
Using the table of values, we have g(3) = 9, and 9(g(3)) = 9.
Therefore, 9(g(3)) = 9.
Thus, the values of the expressions are:
f(g(1)) = 1,
g(f(5)) = 4,
f(f(9)) = 6,
9(g(3)) = 9.
To know more about expressions visit :
https://brainly.com/question/28170201
#SPJ11
let x denote the number of canon slr cameras sold during a particular week by a certain store. the pmf of x is x 0 1 2 3 4 px(x) 0.1 0.2 0.3 0.25 0.15
Answers
P(X = 4, Y = 2) = 0.055131
P(X = Y) = 0.35607
From the information given:
X represent no of Canon SLR
The PMF is given as:
X : 0 1 2 3 4
p(x) : 0.1 0.2 0.3 0.25 0.15
p = P(customers that purchase the camera & also purchase an extended warranty.
As a result, the conditional distribution Y provided X approaches a Binomial distribution with n = x and p = 0.55 as the parameter.
\(\frac{Y}{X}\) ~ Bin ( n= x , p =0.55) y
= 0.1 ........ x and X = 0,1,2,3,4.
The condition probabilities Y given X is:
\(P (\frac{Y = 0}{X = 0} ) =1\)
\(P (\frac{Y = 0}{X = 1} ) = 0.45 and P (\frac{Y = 1}{X = 1} ) =0.55\)
\(P (\frac{Y = 0}{X = 2} ) = 0.2025 and P (\frac{Y = 1}{X = 2} ) =0.495, P (\frac{Y = 2}{X = 2} ) =0.3025\)
\(P (\frac{Y = 0}{X = 3} ) = 0.091125 and P (\frac{Y = 1}{X = 3} ) =0.334125, \\P (\frac{Y = 2}{X = 3} ) =0.408375 and P (\frac{Y = 3}{X = 3} ) = 0.166375\)
\(P (\frac{Y = 0}{X = 4} ) = 0.0.041006 and P (\frac{Y = 1}{X = 4} ) =0.0.200475, P (\frac{Y = 2}{X = 3} ) =0.367538\)
\(P (\frac{Y = 3}{X = 4} ) = 0.299475 and P (\frac{Y = 4}{X = 4} ) =0.091506\)
Now, the joint P.D (probability Dist.) of X & Y is expressed as:
\(P (\frac{Y = y}{X = x} ) = P (\frac{Y = y. X = x}{X = x} )\)
\(P( X = x , Y = y) = P(\frac{Y = y}{X =x} ) * P(X =x)\)
The Joint P.D is;
Y Total
0 1 2 3 4
X 0 0.1 0 0 0 0 0.1
1 0.09 0.11 0 0 0 0.2
2 0.06075 0.1485 0.09075 0 0 0.3
3 0.022781 0.083531 0.102094 0.041594 0 0.25
4 0.006151 0.030071 0.055131 0.044921 0.013726 0.15
Total 0.279682 0.372103 0.247974 0.086515 0.013726 1
(a)
P(X=4,Y=2)
From the table above:
P(X=4,Y=2)
= 0.055131
(b)
P(X= Y)
= (P = 0 , Y = 0) + P( X =1, Y =1) + P( X=2, Y=2) + P(X=3,Y=3) + P(X=4,Y=4)
= 0.1 + 0.11 + 0.09075 + 0.041594 + 0.013726
= 0.35607
Learn more about Probability mass Function:
https://brainly.com/question/18688445
#SPJ4
Solve the word problem below. Enter your answer, using the slash (/) as the
fraction bar.
Students were asked to choose their favorite season and 6/9 chose either
spring or summer. If 5/9 chose spring, what fraction chose summer?
Answers
Answer:
10/9
Step-by-step explanation:
10/9
which statement about qualitative design is true? the goal of many qualitative designs is to permit causal inferences most qualitative designs involve an explicit, preplanned comparison qualitative researchers strive to achieve constancy of conditions in terms of research settings qualitative researchers often put together a complex array of data from a variety of sources
Answers
The true statement about qualitative design is "qualitative researchers regularly prepare a complicated array of records from a variety of sources."
Qualitative research usually includes accumulating records from multiple sources, along with interviews, observations, and files, among others. Researchers analyze those records in-depth to identify themes, styles, and relationships amongst them, frequently the use of an iterative technique to refine their expertise.
at the same time as qualitative research can offer valuable insights into complex phenomena, it isn't commonly designed to permit causal inferences, as it frequently involves small samples and is centered on exploring the reviews and views of contributors in place of testing hypotheses or making predictions.
Qualitative research may additionally contain some level of assessment, however that is commonly not pre-planned and can be extra exploratory in nature. in addition, reaching constancy of conditions in terms of research settings isn't always normally a number one goal of qualitative studies.
Learn more about Qualitative research:-
https://brainly.com/question/24197126
#SPJ4