Which of the following choices can be used to check the answer in this equation?
205 – 110 = 95
Answers
Answer:
Step-by-step explanation:
95+110 should equal 205 if 95 is the answer. This is how you check it.
Related Questions
Medical researchers have determined that for exercise to be beneficial, a person’s desirable heart rate, r, in beats per minute, can be approximated by the formulas r = 143 minus 0.65 a for women r = 165 minus 0.75 a for men, where a represents the person’s age. if the desirable heart rate for a man is 135 beats per minute, how old is he? a. 22.5 years old b. 40 years old c. 45 years old d. 42.5 years old
Answers
Age will be 40 years old.
R, in beats per minute, can be approximated by the formulas, where a represents the person's age.
where R= 143 - 0.65a for women.... (1)
and R= 165 - 0.75a for men,..... (2)
So by implementing these two equation we get a = 40
If the sum of ages is X and Y, and the ratio of their ages is p:q, then the age of Y can be calculated using the formula shown below: Y's age = Y's ratio/Sum of ratios x sum of ages The age dependency ratio is the ratio of dependents (people under the age of 15 or over the age of 64) to the working-age population (people between the ages of 15 and 64). The proportion of dependents per 100 working-age population is shown in the data.
Learn more about Age here
https://brainly.com/question/26423521
#SPJ4
16227Find the exact value of z.2=
Answers
Do you have a picture of your question?
To solve this problem, I'll use proportions.
\(\begin{gathered} \frac{27}{16}\text{ = }\frac{z}{27} \\ z\text{ = 27}\frac{27}{16} \\ z\text{ = }\frac{27^2}{16} \\ z\text{ = }\frac{729}{16} \\ z\text{ = 45.56} \end{gathered}\)Result z = 45.56
It's correct
find the answer to this question
4.2÷0.07
Answers
4.2 divided by 0.07 is 60
Answer:
60
Step-by-step explanation:
Make 4.20 to 420
Make 0.07 to 7
We do this so they can be whole numbers not decimals. (also because it is easier)
420÷7=60
60
I hope this helped! :)
HURRY!! A church group set off from their church at 9:00AM for the beach. The group had to change a tire at 9:31AM. The group noted that the trip took them 63 minutes to finish. What time did the church group arrive at the beach?
Answers
answer:
10:03 am
explanation:
9:00 am + 1 hour (60 min) + 3 min = 10:03 am.
4. Ayla purchased two pairs of jeans for $30.50 and a shirt for $20.75. She paid with a one hundred dollar bill
How much change will Ayla get back?
851.25
$48.75
$81.75
$18.25
Answers
Answer:
i believe its $48.75
Step-by-step explanation:
I didn't know if each pair of jean was 30.50 each. I just did 30.50 + 20.75 to get 51. 25. Then i subtracted that from 100, 100- 51.25, to get 48.75
Consider the probability distribution of the random variable X
X P(X)
0 0.1
1 0.2
2 0.3
3 ?
a. Find the missing (?) probability value
b. Find E(X).
c. Find Var(X) and x.
d. If Z = 1 + 2/3X, find E(Z), Var(Z) and z.
Answers
a. The missing probability value is 0.4.
b. E(X) = 1.4.
c. Var(X) = 0.56 and σx = 0.75.
d. E(Z) = 2.27, Var(Z) = 2.56, and σz = 1.60.
The given probability distribution of the random variable X shows the probabilities associated with each possible outcome. To find the missing probability value, we know that the sum of all probabilities must equal 1. Therefore, the missing probability can be calculated by subtracting the sum of the probabilities already given from 1. In this case, 0.1 + 0.2 + 0.3 = 0.6, so the missing probability value is 1 - 0.6 = 0.4.
To find the expected value or mean of X (E(X)), we multiply each value of X by its corresponding probability and then sum up the results. In this case, (0 * 0.1) + (1 * 0.2) + (2 * 0.3) + (3 * 0.4) = 0.4 + 0.2 + 0.6 + 1.2 = 1.4.
To calculate the variance (Var(X)) of X, we use the formula: Var(X) = Σ[(X - E(X))^2 * P(X)], where Σ denotes the sum over all values of X. The standard deviation (σx) is the square root of the variance. Using this formula, we find Var(X) = [(0 - 1.4)² * 0.1] + [(1 - 1.4)^2 * 0.2] + [(2 - 1.4)² * 0.3] + [(3 - 1.4)² * 0.4] = 0.56. Taking the square root, we get σx = √(0.56) ≈ 0.75.
Now, let's consider the new random variable Z = 1 + (2/3)X. To find E(Z), we substitute the values of X into the formula and calculate the expected value. E(Z) = 1 + (2/3)E(X) = 1 + (2/3) * 1.4 = 2.27.
To calculate Var(Z), we use the formula Var(Z) = (2/3)² * Var(X). Substituting the known values, Var(Z) = (2/3)² * 0.56 = 2.56.
Finally, the standard deviation of Z (σz) is the square root of Var(Z). Therefore, σz = √(2.56) = 1.60.
Learn more about probability value
brainly.com/question/30897652
#SPJ11
Can someone help please this so due tonight

Answers
The fraction of crayons that are blue triangle is 1/5.
The ratio of blue rounds to non-blue crayons is
The fraction of footballs that are brown rubber footballs is 8/15 and here are 4 times as many rubber footballs as non-rubber footballs
What is Fraction?A fraction represents a part of a whole.
1. Let's say Alexa had a total of 5x crayons in the bag.
the number of blue crayons in the bag is 2x,
There is one triangle for every two round crayons,
(1/2) × 2x = x (By condition)
So, the fraction of crayons that are blue triangle is x / 5x = 1/5.
The number of blue round crayons is 2x.
The number of non-blue crayons is 5x - 2x = 3x,
The ratio of blue rounds to non-blue crayons is 2x / 3x = 2/3.
2.
4 out of 5 wall footballs are rubber, 4/5 of the footballs in the bag are rubber.
The fraction of rubber footballs that are brown is 2/3.
The fraction of footballs that are brown rubber footballs is (4/5) × (2/3) = 8/15.
The fraction of non-brown rubber footballs is (4/5) - (8/15) = 4/15.
The ratio of rubber footballs to non-rubber footballs is (4/5) / (1/5) = 4.
So there are 4 times as many rubber footballs as non-rubber footballs
Hence, the fraction of crayons that are blue triangle is 1/5.
The ratio of blue rounds to non-blue crayons is
The fraction of footballs that are brown rubber footballs is 8/15 and here are 4 times as many rubber footballs as non-rubber footballs
To learn more on Fractions click:
https://brainly.com/question/10354322
#SPJ1
So say someone did 1000 push ups a day for 8 years 2920 days in 8 years and you want to do the same amount but in 2 months how many would you have to do a day
Answers
Answer:
48,667 if you round it..
Step-by-step explanation:
1000x2920 = 2,920,000
divided by 2 months
2,920,000/2 = 1,460,000
and theres 30-31 days in a month
1,460,000/30 = 48,666.67
Mo and Alex share some raisins in the ratio 7:5. Mo gets 14 more raisins than Alex. How many raisins did they share?
Answers
Answer:
8.12:5.8
Step-by-step explanation:
you use adam
add=7+5=12
divied=14 divided by 12=1.16
multiply
7x1.16=8.12
5x1.16=5.8
Answer:84
Step-by-step explanation: first find the difference between 7 and 5 which is 2 this means that 14 = 2 . ? = 7 . ? = 5 . to find the ? = 7 you divide 14 by 2 which is 7. this means that 7 = 1 . multiply 7 by 7 to get 49 .
49 = 7 . do the same thing with ? = 5 , 7 multiplied by 5 = 35 . 35 = 5 .
7:5 = 49:35 . to get How many raisins they shared just get the sum of 49+35 which is 84
find the critical numbers of the function. g(x) = x1/5 − x−4/5
Answers
There are no critical numbers of g(x) since g'(x) does not exist anywhere and g(x) is not differentiable
To find the critical numbers of the function g(x), we need to find the values of x where g'(x) = 0 or g'(x) does not exist.
First, we find g'(x) by using the power rule and the chain rule:
g'(x) = (1/5)x^-4/5 - (-4/5)x^-9/5
g'(x) = (1/5)x^-4/5 + (4/5)x^-9/5
To find where g'(x) = 0, we set the derivative equal to 0 and solve for x:
(1/5)x^-4/5 + (4/5)x^-9/5 = 0
Multiplying both sides by 5x^9/5, we get:
x^5 + 4 = 0
This equation has no real solutions, since x^5 is always non-negative and 4 is positive.
Therefore, there are no critical numbers of g(x) since g'(x) does not exist anywhere and g(x) is not differentiable.
To learn more about differentiable visit:
https://brainly.com/question/24898810
#SPJ11
Eleri books a climbing activity. There are 138 people in total on the activity. The people are put into teams. There are 12 people in each team. Any people left over are in a small group. How many teams are there? Show how many people are in the small group.
Answers
Answer:
12
Step-by-step explanation:
138÷12=11R6
11 + 1 =12
a folder and a paper clip cost $1.10 in total. the folder costs $1.00 more than the clip. how much does the paper clip cost?
Answers
The paper clip costs $0.05 and the folder Costs $1.00 more, which is $1.05. Together, they add up to the total of $1.10.
Let's solve this problem step by step:
Let's assume the cost of the paper clip is x dollars.
According to the information given, the folder costs $1.00 more than the paper clip, so the cost of the folder would be (x + $1.00).
The total cost of the folder and the paper clip is $1.10, so we can write the equation:
x + (x + $1.00) = $1.10
Combining like terms, we have:
2x + $1.00 = $1.10
Subtracting $1.00 from both sides of the equation, we get:
2x = $0.10
Dividing both sides by 2, we find the value of x:
x = $0.10 / 2
x = $0.05
Therefore, the paper clip costs $0.05.
In summary, the paper clip costs $0.05 and the folder costs $1.00 more, which is $1.05. Together, they add up to the total of $1.10.
For more questions on Costs .
https://brainly.com/question/25109150
#SPJ8
Solve please for one two three and four please

Answers
1) 60 - this is an alternate interior angle to given 60* so it’s congruent, or the same, so it is also 60.
2) 30 - the given 60* and 2 make a right angle of 90*, so 90 - 60 = 30. It is also an alternate interior angle with given angle of 30, so it is congruent and also 30.
3) 30 - the triangle sum is 180, The interior angle at the bisect is 90, and the given angle of 60. 180 -90 -60 = 30
4) 60 - right angle sum of 3 and 4 is 90. 90 - 30 of angle 3 = 60
Explanation
Rectangle angle rules
All the interior angles of a rectangle add up to 360°.
Each interior angle is equal to 90 degrees.
The diagonals bisect each other.

What is 11 x 15? plz help...
Answers
Answer: 165.
Step-by-step explanation: You can multiply 11 by 15 to get 165. If that is too difficult, you can multiply 11 by 5 and 11 by 10 and add them. 11*5 is 55 and 11*10 is 110. 110 + 55 = 165.
ANSWER
Find the scale factor of the dilation shown in the diagram. 1/2 1/3 2 3
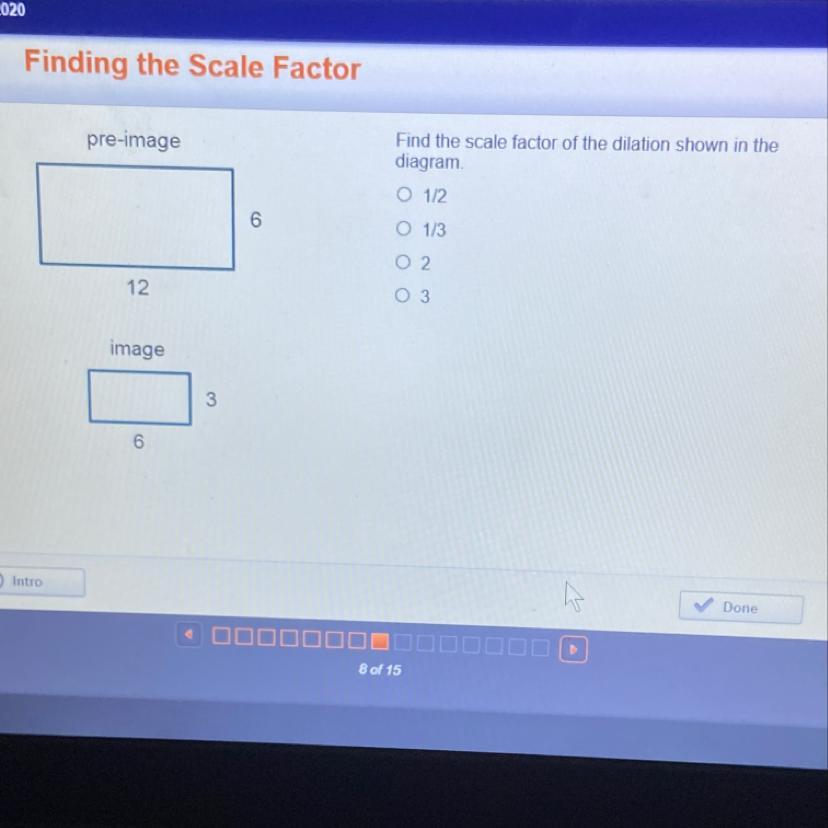
Answers
The scale factor of the dilation shown in the diagram 2.
What is Division method?Division method is used to distributing a group of things into equal parts. Division is just opposite of multiplications. For example, dividing 20 by 2 means splitting 20 into 2 equal groups of 10.
We have to given that;
The image and pre image are shown in figure.
Now, We know that;
The basic formula to find the scale factor of a dilated figure is,
⇒ Scale factor = Dimension of the new shape ÷ Dimension of the original shape.
Substitute the given values, we get;
⇒ Scale factor = 6 / 3
⇒ Scale factor = 2
Thus, The scale factor of the dilation shown in the diagram 2.
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ1
Answer:1/2
Step-by-step explanation:
got it right on edge
which has the least result? A. 3/4-3/4 B. 3/4+3/4 C. -3/4 + 3/4 D. -3/4-3/4?
Answers
Answer: D
Step-by-step explanation:
The solution to both A and C would total to about 0. Also, in B both numbers are positives, so that would also be out of the case. If you are looking for the least value, the answer would be D since -3/4 -3/4 would equal -1.5, (or -1 1/2). Therefore, your answer would be D.
Hope that helps :D
Answer:
D. -3/4 - 3/4
Step-by-step explanation:
A. 3/4 -3/4 = 0
B. 3/4 + 3/4 = 1 1/2
C. -3/4 + 3/4 = 0
D. -3/4 - 3/4 = -1 1/2
Explain what values must be known to write the explicit formula for both an arithmetic and geometric sequence?
PLEATHE!!
Answers
The explicit formula for an arithmetic sequence is:
an = a1 + (n-1)d
The explicit formula for a geometric sequence is:
an = a1 * \(r^{(n-1)}\)
What is arithmetic sequence?
An arithmetic sequence is a sequence of numbers in which each term after the first is found by adding a fixed constant number, called the common difference, to the preceding term.
To write the explicit formula for both an arithmetic and geometric sequence, the following values must be known:
For an Arithmetic Sequence:
The first term (a1) of the sequence.
The common difference (d) between consecutive terms in the sequence.
The explicit formula for an arithmetic sequence is:
an = a1 + (n-1)d
Where:
an is the nth term of the sequence.
a1 is the first term of the sequence.
d is the common difference between consecutive terms.
n is the position of the term in the sequence.
For a Geometric Sequence:
The first term (a1) of the sequence.
The common ratio (r) between consecutive terms in the sequence.
The explicit formula for a geometric sequence is:
an = a1 * r^(n-1)
Where:
an is the nth term of the sequence.
a1 is the first term of the sequence.
r is the common ratio between consecutive terms.
n is the position of the term in the sequence.
Therefore, The explicit formula for an arithmetic sequence is:
an = a1 + (n-1)d
The explicit formula for a geometric sequence is:
an = a1 * \(r^{(n-1)}\)
To learn more about arithmetic sequence from the given link:
https://brainly.com/question/15412619
#SPJ1
Matina made deposits of $2,000 at the beginning of each year for four years. The rate she earned is 5% annually. What's the value of Martina's account in four years?
Answers
The value of Matina's account in four years, considering the $2,000 deposits at the beginning of each year and a 5% annual interest rate, would be approximately $8,620.25.
To calculate the value of Matina's account in four years, we can use the formula for the future value of an ordinary annuity.
The formula is:
\(FV = P \times [(1 + r)^n - 1] / r\)
Where:
FV is the future value of the annuity
P is the periodic payment or deposit amount
r is the interest rate per period
n is the number of periods.
P = $2,000 (deposit amount)
r = 5% = 0.05 (annual interest rate)
n = 4 (number of years)
Plugging in the values into the formula:
\(FV = $2,000 \times[(1 + 0.05)^4 - 1] / 0.05.\)
Simplifying the expression:
\(FV = $2,000 \times [1.05^4 - 1] / 0.05\)
Calculating the exponential term:
\(1.05^4\approx 1.21550625\)
Plugging in the calculated value:
\(FV = $2,000 \times (1.21550625 - 1) / 0.05\)
\(FV ≈ $2,000 \times 0.21550625 / 0.05\)
FV ≈ $8,620.25
For similar question on annual interest rate.
https://brainly.com/question/31261623
#SPJ8
Jared made a scale drawing of his classroom for his tech project. He used a scale of 1 cm = 3.5 ft. If the length of his classroom on the drawing measured 30 cm, What is the actual length of his classroom?
Answers
Answer: 105ft
Step-by-step explanation: If 1cm is 3.5ft then you should multiply 3.5ft by 30 cm to get 105ft.
asymptotic distribution of x(n-x)/n(n-1)
Answers
Asymptotic distribution of x(n-x)/n(n-1) is 0.
Let's discuss it further below.
To find the asymptotic distribution of x(n-x)/n(n-1), we will follow these steps:
1. Rewrite the expression as a ratio of two variables: X = x/n and Y = (n-x)/n.
2. Rewrite the expression in terms of X and Y: Z = X * Y / ((X + Y) * (X + Y - 1)).
3. Find the limit of Z as n approaches infinity, which represents the asymptotic distribution.
Let's proceed with these steps:
1. Rewrite the expression as a ratio of two variables:
X = x/n and Y = (n-x)/n
2. Rewrite the expression in terms of X and Y:
Z = X * Y / ((X + Y) * (X + Y - 1))
3. Find the limit of Z as n approaches infinity:
Since X = x/n and Y = (n-x)/n, as n approaches infinity, both X and Y will approach 0. Therefore, the limit of Z as n approaches infinity is 0.
In conclusion, the asymptotic distribution of x(n-x)/n(n-1) is 0.
Learn more about asymptotic distribution.
brainly.com/question/30077272
#SPJ11
Determine the two unit vectors in which the directional derivative of f at (a,b) is equal to zero. Show your work.
f(x,y)=x^3y-x^2y^2
x=6
y=2
Answers
Therefore, the two unit vectors in which the directional derivative of f at (6,2) is equal to zero are:
v_1 = <-9/10, √(100/81)> ≈ <-0.707, 0.707>
v_2 = <-9/10, -√(100/81)> ≈ <-0.707, -0.707>
The directional derivative of a function f(x,y) at point (a,b) in the direction of a unit vector v = <u, v> is given by the dot product of the gradient of f at (a,b) and v:
D_v(f) = ∇f(a,b) · v
where ∇f(a,b) is the gradient of f at (a,b).
To find the unit vectors in which the directional derivative of f at (a,b) is equal to zero, we need to find the gradient of f at (a,b) and then solve for v such that D_v(f) = 0.
First, we find the gradient of f(x,y):
∇f(x,y) = <∂f/∂x, ∂f/∂y>
= <3x^2y-2xy^2, x^3-2xy>
Now, we evaluate the gradient at (a,b) = (6,2):
∇f(6,2) = <3(6)^2(2)-2(6)(2)^2, (6)^3-2(6)(2)>
= <204, 180>
Next, we solve for v such that D_v(f) = 0:
D_v(f) = ∇f(6,2) · <u, v>
= 204u + 180v
Setting D_v(f) = 0, we get:
204u + 180v = 0
u = -9/10 v
Since v is a unit vector, we have:
1 = ||<u, v>||^2
= u^2 + v^2
= (-9/10)^2v^2 + v^2
= (81/100)v^2
Solving for v, we get:
v = ± √(100/81)
v_1 = <-9/10, √(100/81)> ≈ <-0.707, 0.707>
v_2 = <-9/10, -√(100/81)> ≈ <-0.707, -0.707>
To know more about directional derivative,
https://brainly.com/question/20733439
#SPJ11
Which expression shows a way to find 22 x 46?
(22 x 4) + (22 x 6)
(22 x 40) + (22 x 6)
(11 x 40) + (11 x 6)
(2 x 4) + (2 x 6)
Answers
Step-by-step explanation:
We can use the expression (22 x 40) + (22 x 6).
I NEED HELP THIS WORKSHEET IS DUE IN AN HOUR!!!!!!!!
14/15 + x = 4/9
Answers
Answer:
So let's rearrangeWe get x= -22/45
Solve the following differential equation by using the method of Laplace transforms \[ y^{\prime \prime}-y^{\prime}-2 y=t, y(0)=2, y^{\prime}(0)=0 \]
Answers
The solution to the given differential equation is:
\(\[ y(t) = -\frac{1}{2} + \frac{5}{4}e^{2t} + \frac{1}{4}(t+2) \]\).
1. Taking the Laplace transform of the given differential equation, we have:
\(\[ s^2 Y(s) - sy(0) - y'(0) - (sY(s) - y(0)) - 2Y(s) = \frac{1}{s^2} \]\)
Substituting the initial conditions (y(0) = 2) and (y'(0) = 0), we simplify the equation to:
\(\[ s^2 Y(s) - 2s - sY(s) - 2Y(s) = \frac{1}{s^2} \]\)
2. Rearranging the terms and solving for (Y(s)), we get:
\(\[ Y(s) = \frac{2s + 1}{(s^2 - s - 2)(s^2)} \]\)
3. Decompose the right side into partial fractions:
\(\[ Y(s) = \frac{A}{s} + \frac{B}{s-2} + \frac{Cs+D}{s^2} \]\)
Multiply through by the common denominator to get:
\(\[ 2s + 1 = A(s-2) + B(s^2) + (Cs+D)(s-2) \]\)
Expanding and comparing coefficients, we find:
\(\[ A = -\frac{1}{2}, \quad B = \frac{5}{4}, \quad C = \frac{1}{4}, \quad D = \frac{1}{2} \]\)
So, the partial fraction decomposition of (Y(s)) is:
\(\[ Y(s) = -\frac{1}{2s} + \frac{5}{4(s-2)} + \frac{s+2}{4s^2} \]\)
4. Take the inverse Laplace transform of (Y(s)) using Laplace transform table or formula. After simplifying the fractions, we obtain the solution in the time domain:
\(\[ y(t) = -\frac{1}{2} + \frac{5}{4}e^{2t} + \frac{1}{4}(t+2) \]\)
Therefore, the solution to the given differential equation is:
\(\[ y(t) = -\frac{1}{2} + \frac{5}{4}e^{2t} + \frac{1}{4}(t+2) \]\).
Learn more about Laplace Transform at:
https://brainly.com/question/29583725
#SPJ4
A 5-inch candle burns down in 11 hours. Assuming the candles are the same
thickness and make (that is, directly proportional), how long would it take a 4-inch
candle to burn down?
Answers
The time to burn 4 inches is 8.8 hours
How to determine the time to burnFrom the question, we have the following parameters that can be used in our computation:
A 5-inch candle burns down in 11 hours.
This can be expressed as
Time : Length = 11 hours : 5 inches
For 4 inches, we have
Time : 4 inches = 11 hours : 5 inches
Express as fraction
Time = 4 * 11/5
Evaluate
Time = 8.8
Hence, the time is 8.8 hours
Read more about rate at
brainly.com/question/24178013
#SPJ1
Select interior, exterior, or on the circle (x - 5) 2 + (y + 3) 2 = 25 for the following point.
(5, 2)
exterior
interior
on the circle
Answers
For the point (x, y), calculate the distance from the center using the distance formula:
Distance = sqrt((x - 5)^2 + (y + 3)^2)
The given equation represents a circle with center (5, -3) and radius 5. To determine if a point is inside, outside, or on the circle, we can compare the distance from the point to the center with the radius.
Next, compare the distance to the radius (5) to determine the point's location:
1. If Distance < 5, the point is in the interior of the circle.
2. If Distance = 5, the point is on the circle.
3. If Distance > 5, the point is in the exterior of the circle.
Using these criteria, you can classify any given point as interior, exterior, or on the circle.
To learn more about : distance
https://brainly.com/question/26046491
#SPJ11
in euclidean geometry the sum of the angles in a triangle equals 180 degrees. is this also true in spherical geometry?
Answers
The statement is not true for spherical geometry. Because the sum of the angles in a triangle in spherical geometry is not equal to 180 degrees.
"Information available from the question"
In the question:
In Euclidean geometry the sum of the angles in a triangle equals 180 degrees.
We have to identify that this is true for spherical geometry also;
Now, According to the question:
In a Euclidean space, the sum of angles of a triangle equals the straight angle (180 degrees, π radians, two right angles, or a half-turn). A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
The sum of the angles of a spherical triangle is not equal to 180°. A sphere is a curved surface, but locally the laws of the flat (planar) Euclidean geometry are good approximations. In a small triangle on the face of the earth, the sum of the angles is only slightly more than 180 degrees.
Learn more about Euclidean geometry at:
https://brainly.com/question/4637858
#SPJ4
What is the measure of \angle D∠Dangle, D?

Answers
Answer:
74⁰
Step-by-step explanation:
As in cyclic quadrilateral sum of opposite angles us equal to 180⁰
someone answer this correctly please, I’ll give you brainliest and your getting 50 points someone answer this no fraud answers don’t be weird.

Answers
The proof of the congruent sides RU and TS is given below.
What is congruent triangles?
In any orientation, two triangles are said to be congruent if their three sides and three angles are equal.
Therefore, if two triangles have the same number of sides on each side, they are said to be congruent. Additionally, we can determine that they are congruent if we have a side, an angle between the sides, and then another side that is congruent, in that order: side, angle, side.
Let the given figure is a rectangle RSTU.
Since the all four angles of rectangle are of 90 degree.
So, each angle of rectangle RSTU is 90 degree.
Let, US divides the angle RUT and angle RST and form two new triangles, ΔSRU and ΔSTU.
Both the triangles having same measure of angles and sides.
⇒ ΔSRU ≅ ΔSTU
As the triangles are congruent so their sides are congruent.
Hence, RU is congruent to TS.
To know more about congruent triangles, click on the link
https://brainly.com/question/29789999
#SPJ1
the aquarium has 3 more yellow fish than green fish. 60% of the fish are yellow. how many green fish are in the aquarium? show your work.
Answers
The number of green fish are in the aquarium is 6.
Given that,
The aquarium has 3 more yellow fish than green fish.
60 percent of the fish are yellow.
Let us assume the green fishes be x and the yellow fishes are y.
Total no of fished = x + y.
And, y = x + 3
Based on the above information, the calculation is as follows:
Now, put y = x + 3
So,
60%(y+x)=y
\(\frac{60}{100}(x+3+x)=x+3\)
60(2x+3)=100(x+3)
120x + 180 = 100x + 300
20x = 120
x = 6
Hence the number of green fishes are x=6
To learn more about linear equations, visit:
https://brainly.com/question/29268835
#SPJ4