Answers
Answer:
Second photo
I hope this helps!


Related Questions
in , the sports league introduced a salary cap that limits the amount of money spent on players' salaries. the quadratic model approximates this cap in millions of dollars for the years -, where x0 represents , x1 represents , and so on. complete parts a and b.
Answers
a) The approximate sports league salary cap in 1995 was $35.17 million. b) According to the model, the salary cap reached $65 million in the year 2001.
To approximate the sports league salary cap in millions of dollars for a given year using the quadratic model, we substitute the corresponding value of x into the equation \(y = 0.2313x^2 + 2.600x + 35.17\).
a) To approximate the sports league salary cap in a particular year, we need to determine the value of y when x represents that year. Let's calculate:
For the year 1995 (x = 0):
\(y = 0.2313(0)^2 + 2.600(0) + 35.17\)
y ≈ 35.17 million dollars
Therefore, the sports league salary cap in 1995 was approximately 35.17 million dollars.
b) We can use the quadratic equation to determine the year when the salary cap reached 65 million dollars. Let's solve the equation for y = 65:
\(65 = 0.2313x^2 + 2.600x + 35.17\)
To solve this quadratic equation, we can rearrange it to:
\(0.2313x^2 + 2.600x + 35.17 - 65 = 0\)
\(0.2313x^2 + 2.600x - 29.83 = 0\)
To solve this equation, we can use the quadratic formula:
x = (-b ± √(b²- 4ac)) / 2a
where a = 0.2313, b = 2.600, and c = -29.83.
Substituting these values into the quadratic formula, we get:
x = (-2.600 ± √(2.600² - 4 * 0.2313 * (-29.83))) / (2 * 0.2313)
Calculating the expression within the square root:
x = (-2.600 ± √(6.76 + 27.4376)) / 0.4626
x = (-2.600 ± √(34.1976)) / 0.4626
x = (-2.600 ± 5.8456) / 0.4626
Now we can calculate the two possible values for x:
x1 = (-2.600 + 5.8456) / 0.4626 ≈ 6.22
x2 = (-2.600 - 5.8456) / 0.4626 ≈ -14.09
The value of x represents the number of years since 1995. Therefore, -14.09 is not a valid solution in this context.
According to the model, the salary cap reached 65 million dollars approximately 6.22 years after 1995. Adding this to 1995, we find:
1995 + 6.22 ≈ 2001.22
Therefore, according to the model, the salary cap reached 65 million dollars around the year 2001.
Learn more about quadratic equation here: https://brainly.com/question/30098550
#SPJ11
The complete question is:
In 1995, the sports league introduced a salary cap that limits the amount of money spent on players' salaries. The quadratic model y=0.2313x2+2.600x+35.17 approximates this cap in millions of dollars for the years 1995-2006, where x=0 represents 1995, x=1 represents 1996, and so on. Complete parts a and b.
a) Approximate the sports league salary cap in .
b) According to the model, in what year did the salary cap reach 65 million dollars?
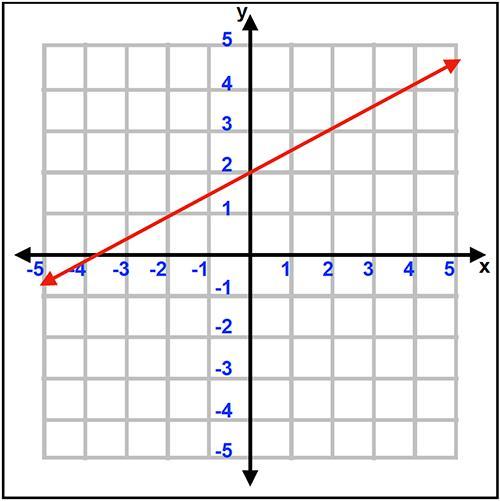
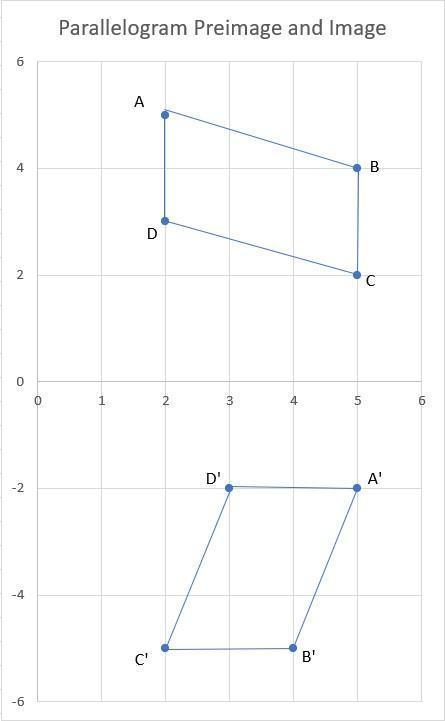
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Select the elements in
A
.
A
=
{
x
:
x
−
3
=
5
}
Answers
Answer:
3
Step-by-step explanation:
Suppose that X1, . . . , Xn form a random sample from a Normal distribution for which mean μ is known, but the variance σ 2 is unknown. Find the MLE (maximum likelihood estimation) of σ.
Answers
the MLE of the unknown variance σ{power}2 of a Normal distribution when the mean μ is known is the sample variance, which is the sum of the squared deviations of the observations from the mean, divided by the sample size.
Suppose X1, . . . , Xn are iid samples from a Normal distribution with mean μ and unknown variance σ{power}2. The likelihood function for this model is given by:
L(σ{power}2|x) = (1/σ{power}(n)) {product} exp(-(1/2σ{power}2) {product}Σ(xi - μ){power}2)
where Σ denotes the sum over i=1 to n.
To find the MLE of σ{power}2, we differentiate the log-likelihood function with respect to σ{power}2 and set the derivative equal to zero:
d/d(σ{power}2) log L(σ{power}2|x) = -(n/2σ{power}2) + (1/2σ{power}4) {product}Σ(xi - μ){power}2 = 0
Solving for σ{power}2, we get:
σ{power}2 = (1/n) {product} Σ(xi - μ){power}2
This means that the MLE of σ{power}2 is the sample variance, which is the sum of the squared deviations of the observations from the mean, divided by the sample size.
To show that this is indeed the MLE, we need to check that it is a maximum. We can do this by computing the second derivative of the log-likelihood function with respect to σ{power2:
d{power}2/d(σ{power}2){power}2 log L(σ{power}2|x) = n/(2σ{power}4) - Σ(xi - μ){power}2/(σ{power}6)
If we plug in the value of σ{power}2 = (1/n) {product} Σ(xi - μ){power}2 into this expression, we get:
d{power}2/d(σ{power}2){power}2 log L((1/n) {product}Σ(xi - μ){power}2|x) = -n/(2((1/n) {product} Σ(xi - μ){power}2){power}2) < 0
This shows that the MLE of σ{power}2 is indeed a maximum.
In conclusion, the MLE of the unknown variance σ{power}2 of a Normal distribution when the mean μ is known is the sample variance, which is the sum of the squared deviations of the observations from the mean, divided by the sample size. This estimator is unbiased and efficient, meaning it has the smallest variance among all unbiased estimators.
To know more about MLE click here:
brainly.com/question/30447662
#SPJ4
Mariya is solving the quadratic equation by completing the square.
4x2-20x+3=0
4x2-20x=-3
A(x2-5x)=-3
Mariya is solving the quadratic equation by completing the square.
4x2-20x+3=0
4x2-20x=-3
A(x2-5x)=-3
What is the value of A?
-20
3
4
5
Answers
Answer:
4
Step-by-step explanation:
just 4 -_-
4x^2-20x
=4(x^2-5x)
so the value is 4
By solving the quadratic equation, the value of A is 4
Option (3) is correct.
What is a quadratic equation?A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is \(ax^{2}+bx+c=0\), where a and b are the coefficients, x is the variable, and c is the constant term.
Given quadratic equation
\(4x^{2} -20x+3=0\)
⇒ \(4x^{2} -20x=-3\)
By taking 4 as common in \(4 x^{2}\) and 20x
⇒ \(4(x^{2} -5x)=-3\)...................(1)
According to the question by solving the quadratic equation. Mariya got, \(A(x^{2} -5x)=-3\) .....................(2)
By comparing equation 1 and 2 we can clearly see that A = 4
Hence, by solving the quadratic equation, the value of A is 4
Option (3) is correct.
Learn more about quadratic equation here
https://brainly.com/question/1863222
#SPJ2
(9-6)x8+2 CAN SOMEONE HELP PLS AND THANK U
Answers
3x8+2
24+2
answer= 26
Answer:
26
Step-by-step explanation:
This is what I got! I hope this helps!
A factory produces 100 units of a certain product and 6 of them are defective. If three units are picked at random then what is the probability that at least one of them is defective?.
Answers
The probability that at least one of them is defective if three units are picked at random is 0.8560.
We would define Ai as the event that the i th chosen unit is not defective, for I = 1, 2, 3. We are interested in P (A1 ∩ A2 ∩ A3). Note that
P(A1) = 95/100
Given that the first chosen item was good, the second item will be chosen from 94 good units and 5 defective units, thus
P (A2 ∣ A1) = 94/99
Given that the first and second chosen items were okay, the third item will be chosen from 93 good units and 5 defective units, thus
P (A3∣ A2, A1) = 93/98
Thus, we have
P(A1∩ A2 ∩ A3) = P(A1) P(A2∣ A1) P(A3∣ A2, A1)
=95/100*94/99*93/98
=0.8560
To learn more about probability. Click, https://brainly.com/question/21333099
#SPJ4
Find the Area of the triangle below

Answers
Answer:20.25
Step-by-step explanation:
I NEED PROBLEM 3 BUT they said something to do with 2nd problem.2ND PROBLEM IN THE COMMENTS

Answers
Answer:
Sssssnake ssssssnake sssssnake........../////////////////////////................
Step-by-step explanation:
Consider the following function f(x)=x4+3, x>=0.Find an explicit formula for f^-1
Answers
The explicit formula for f^-1 is (x-3)^(1/4) and this is obtained by switching the roles of x and y and solving for y in terms of x.
To find the inverse function of f(x)=x^4+3, we need to switch the roles of x and y, and solve for y.
Let y = x^4+3
Subtract 3 from both sides to get:
y - 3 = x^4
Take the fourth root of both sides to isolate x:
(x^4)^(1/4) = (y-3)^(1/4)
Simplify:
x = (y-3)^(1/4)
So the inverse function of f(x) is:
f^-1 (x) = (x-3)^(1/4)
This is the explicit formula for the inverse function of f(x).
To know more about explicit formula visit:
https://brainly.com/question/18069156
#SPJ11
Which ordered pair is the vertex of ?
Answers
Answer:
Got this from the internet.
Step-by-step explanation:
The vertical line dividing the parabola into two equal portions is called the line of symmetry. All parabolas have a vertex, the ordered pair that represents the bottom (or the top) of the curve. The vertex of a parabola has an ordered pair \begin{align*}(h, k)\end{align*}.

Students wash cars to raise funds for class trips. The class made a profit of $326.60 from last Saturday’s car wash, which was 92% of its revenue. How much was the revenue(commission) for the car wash? (plsssssss answer someone)
Answers
Answer:627.072
Step-by-step explanation:
A solution to the equation 4x+2y=20 must also be a solution to which of the following equations?1) 8x+2y=402) 2x+2y=103) 2x+y=104) 4x+4y=40
Answers
As given by the question,
There are given that the equation:
\(4x+2y=20\)Now,
First, suppose any number, for which the given equation has satisfied.
So, the number is, x = 2 and y = 6
Then,
Put both values into the given equation
\(\begin{gathered} 4x+2y=20 \\ 4(2)+2(6)=20 \\ 8+12=20 \\ 20=20 \end{gathered}\)Then,
Put the same value of x and y into the given option and check whether it is satisfied:
So,
From option 3:
\(\begin{gathered} 2x+y=10 \\ 2(2)+6=10 \\ 4+6=10 \\ 10=10 \end{gathered}\)Hence, the correct option is 3.
f ( x ) = − x + 1 f(x)=−x+1, find f ( − 1 ) f(−1).
Answers
\(f(x) = - x + 1 \iff f(-1) = - (-1) + 1 = 1+1 = 2\)
\(\implies \bf f(-1) = 2\)
Answer: f(-1) = 2
Step-by-step explanation:
To find f(-1), we simply need to substitute -1 for x in the given expression for f(x):
f(x) = -x + 1
f(-1) = -(-1) + 1 [substitute x=-1]
f(-1) = 1 + 1
f(-1) = 2
MAKE ME THE BRAINLIEST PLS
A) Suppose that the events A and B are disjoint. Under what conditions are AC and BC disjoint? B) Suppose that a committee of 12 people is selected in a random manner from a group of 100 people. Determine the probability that two particular people A and B will both be selected.
Answers
Tthe probability that two particular people A and B will both be selected is:
P(A and B) = (2! * C(98,10)) / C(100,12)
How we prove it?A) If events A and B are disjoint, it means that they have no elements in common, i.e., A ∩ B = ∅. In this case, AC and BC are disjoint if and only if AC and BC have no elements in common, i.e., (AC) ∩ (BC) = ∅.
B) To find the probability that two particular people A and B will both be selected, we need to find the number of favorable outcomes (where both A and B are selected) and divide it by the number of total possible outcomes (the number of ways to select 12 people from 100).
The number of favorable outcomes is the number of ways to select the two people A and B, which is 2!, and the number of ways to select the remaining 10 people, which is (100-2) choose 10, i.e., C(98,10). So, the number of favorable outcomes is 2! * C(98,10).
The number of total possible outcomes is the number of ways to select 12 people from 100, which is C(100,12).
So, the probability that two particular people A and B will both be selected is:
P(A and B) = (2! * C(98,10)) / C(100,12)
What is probability?Probability is a mathematical concept that quantifies the likelihood of an event occurring. It is a value between 0 and 1, where 0 represents an event that is impossible to occur, and 1 represents an event that is certain to occur.
Probabilities can be calculated based on the number of favorable outcomes (the number of ways the event of interest can occur) and the number of possible outcomes (the number of possible outcomes in the sample space).
For example, if you roll a fair six-sided die, the probability of rolling a 4 is 1/6, because there is only one favorable outcome (rolling a 4) out of six possible outcomes (rolling a 1, 2, 3, 4, 5, or 6).
Probability is used in many fields, including mathematics, statistics, finance, insurance, and the natural sciences, to make predictions and inform decision-making under uncertainty.
Learn more about probability here
https://brainly.com/question/30034780
#SPJ1
PLS HELP I REALLY NEED HELP

Answers
Answer:
a) AB = 10 unitsb) Midpoint is (2, 6)===================
GivenPoints A( - 1, 10) and B(5, 2)To finda) The length of ABb) The midpoint of ABSolutiona) Use the distance formula:
\(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Substitute the coordinates and calculate:
\(d=\sqrt{(5-(-1))^2+(2-10)^2} =\sqrt{6^2+(-8)^2} =\sqrt{36+64} =\sqrt{100} =10\)
The distance is AB = 10 units
b) Use midpoint formula and find x and y- coordinates of this point:
\(x= \cfrac{x_1+x_2}{2}\) and \(y= \cfrac{y_1+y_2}{2}\)
Substitute coordinates and find the midpoint:
\(x= \cfrac{-1+5}{2} =2\) and \(y= \cfrac{10+2}{2}=6\)
The midpoint is (2, 6)
Answer:
Length of line segment AB = 10 units
Midpoint of line segment AB = (2, 6)
Step-by-step explanation:
To find length, apply the distance formula :
AB = √(5 - (-1))² + (2 - 10)²AB = √36 + 64 = √100\(\fbox {AB = 10 units}\)To find the midpoint :
M = (-1 + 5 / 2, 10 + 2 / 2)\(\fbox {Midpoint = (2, 6)}\)Round to the nearest ten, then estimate the product. 35 x 99 = ___
a. 2,700
b. 3,000
c. 3,600
d. 4,000
Answers
Answer:
The answer is 4,000.
Step-by-step explanation:
The closest to 35xn= 3,465
Answer:
Step-by-step explanation:
35 to the nearest 10 is 40 and 99 to the nearest 10 is 100 so 4 times 100 is 4,000 so your answer should be d. 4,000
Write each fraction in simplest form. Write simplified if the fraction is already simplest form. 6/16a 1/3 b. 12/32c. 3/8d. simplified
Answers
Given:
\(\frac{6}{16}\)To find:
Write each given fraction in the simplest form.
Explanation:
Write given terms in numerator and denominator as factorize form,
\(\frac{6}{16}=\frac{3\times2}{8\times2}\)Cancel out the common terms in numerator and denominator,
\(\frac{6}{16}=\frac{3}{8}\)Which is the simplest form.
Final answer:
Hence, the required simplest form is:
what’s the solution by graphing?

Answers
Find the distance between points P(9,8) and Q(7,6) to the nearest tenth.
Answers
Answer:
2.8 units
Step-by-step explanation:
Think of this distance as the hypotenuse of a right triangle that has a vertical leg and a horizontal one as well.
Going from P to Q, the change in x is 2 and the change in y is also 2.
Thus, by the Pythagorean Theorem, this desired distance is:
d = √(2^2 + 2^2) = 2√2 units, or 2.8 units
what is the difference between the critical value of z and the observed value of z (test statistic)?
Answers
The critical value of z separates the rejection region from the nonrejection region while observed value of z is the value calculated for a sample statistic such as x.
A critical value of z is used when the sampling distribution is normal, or close to normal. The critical value of z refers to the point that cuts off area under graph for the standard normal distribution separating the rejection and nonrejection region of the data. The Critical value of z can indicate what probability any particular variable will have. These values are typically obtained from a table such as the standard normal distribution table. The observed value of z is a value determined for a sample statistic x. It is a test statistic for Z-tests that measures the difference between an observed statistic and its hypothesized population parameter in units of the standard deviation.
Learn more about Critical value of z:
https://brainly.com/question/15728178
#SPJ4
7x + 3(5 - 3x) =5
i keep seeing answers on here claiming to be step by step but i end up confused. what is x equal to?
Answers
Answer:
x=5
Step-by-step explanation:
7x+15-9x=5
-2x+15=5
-2x=-10
x=5
Answer:
X = 5
Step-by-step explanation:
First expand, 7x + 15 - 9x = 5
Simplify, -2x + 15 = 5
Additive property of Addition/Subtraction , (-2x + 15) - 15 = (5) -15
Simplify, -2x = -10
Divide by -2, (-2x)/-2 = (-10)/-2
Simplify, x = 5
Substitution for checking your answer, 7(5) + 3(5-3(5)) = 5
35 + (15-45), simplify, 35 - 30 = 5
Thus the final answer can be concluded as X = 5
the square root of 90 is it closer to 9 or 10
Answers
Answer:
9
Step-by-step explanation:
9² = 81
10² = 100
81 ... 90 ... 100
90 - 81 = 9
100 - 90 = 10
9 is less than 10
Hence, √90 is closer to 9
The shirt was $7.45 he pays with a $20 how much he getting back
Answers
Answer:
$12.55
Step-by-step explanation:
20-7.45=12.55
please help, need asap

Answers
Answer:
x= 1
y= 3
Step-by-step explanation:
21(-2+y) +7y = 42
-42 +28y+42
28y = 42+42
28y= 84
divide both sides y= 3
x= -2+3 x=1
x= + (3-2) = 1
42=42
10=10
The volume of a rectangular prism can be found by multiplying the base area, B, times the height. If the volume of the prism is represented by 15x2 + x + 2 and the height is x2, which expression represents B, the area of the base? 15x + + 15x + + 15 + + 15 + +
Answers
Answer:
\(Base (B) = /frac{15x² + 1 + 2}{x}\)
Step-by-step Explanation:
==>Given:
Dimensions of a rectangular prism are expressed as follow:
Volume (V) = 15x² + x + 2
Height (h) = x²
==>Required:
Expression of the Base area (B)
==>Solution:
Volume (V) = Base (B) × Height (h)
15x² + x + 2 = B × x²
Divide both sides by x²
\(\frac{15x² + x + 2}{x²} = B
\(Base (B) = /frac{15x² + 1 + 2}{x}\)
Answer: c
Step-by-step explanation:
given sine of x equals negative 15 over 17 and cos x > 0, what is the exact solution of cos 2x? 161 over 289 225 over 289 negative 161 over 289 negative 225 over 169
Answers
The value of cos2x when sine of x equals negative 15 over 17 and cos x > 0 is -161/289.
What is cosine function?The ratio of the neighboring side's length to the longest side, or hypotenuse, in a right triangle is known as the cosine. Let's say that the hypotenuse of a triangle ABC is written as AB, and the angle between the hypotenuse and base is written as.
It's interesting to see that cos's value varies depending on the quadrant. As observed in the above table, cos 0°, 30°, etc. have positive values while cos 120°, 150°, and 180° have negative values. Cos will have a good value in the first and fourth quadrants.
Given that, sin x equals negative 15 over 17.
Using the Pythagoras theorem we have:
(17)² = (- 15)² + y²
y = 8
The value of cos x = 8/17
Then the value of cos2(x) is calculated using the formula:
cos2x = cos²x - sin²x
cos2x = (8/17)² - (15/17)²
cos2x = -161/289
Hence, the value of cos2x when sine of x equals negative 15 over 17 and cos x > 0 is -161/289.
Learn more a cosine function here:
https://brainly.com/question/29277391
#SPJ1
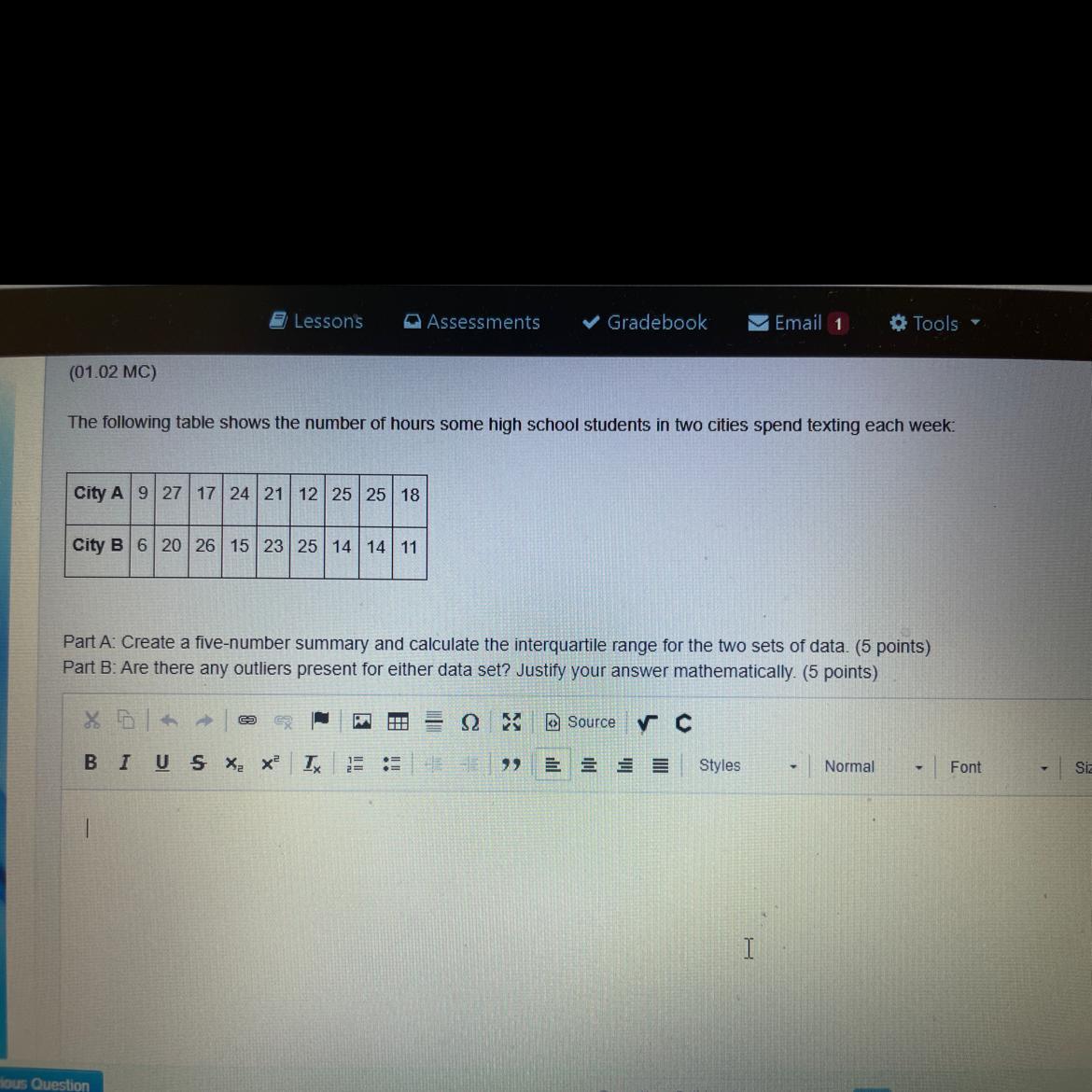
The following table shows the number of hours some middle school students in two cities spend texting each week: City A 9 27 17 24 21 12 25 25 18 City B 6 20 26 15 23 25 14 14 11 Part A: Create a five-number summary and calculate the interquartile range for the two sets of data. (5 points) Part B: Are there any outliers present for either data set ?Justify your answer. (5 points)
Answers
A. Five-number summary for City A and B are given below. IQR for City A is 10.5; IQR for City B is 11.5
B. There are no outliers present in either data set.
What is the Five-number Summary?The values in the five-number summary include, lower and upper quartiles, max and min values, and the median.
What is the Interquartile Range (IQR)?Interquartile range (IQR) = upper quartile (Q3) - lower quartile (Q1)
What is an Outlier?Outlier of a data set is any value that is lower than Q1 - 1.5 × IQR or greater than Q3 + 1.5 × IQR.
The five-number summary for City A, 9, 27, 17, 24, 21, 12, 25, 25, 18, is:
Minimum: 9Quartile Q1: 14.5Median: 21Quartile Q3: 25Maximum: 27IQR = 25 - 14.5 = 10.5
Outlier for City A:
Q1 - 1.5 × IQR = 14.5 - 1.5 × 10.5 = -1.25
Q3 + 1.5 × IQR = 25 + 1.5 × 10.5 = 40.75
No value is less than -1.25 or greater than 40.75, therefore, there is no outlier in City A.
The five-number summary for City B, 6, 20, 26, 15, 23, 25, 14, 14, 11, is:
Minimum: 6Quartile Q1: 12.5Median: 15Quartile Q3: 24Maximum: 26IQR = 24 - 12.5 = 11.5
Outlier for City B:
Q1 - 1.5 × IQR = 12.5 - 1.5 × 11.5 = -4.75
Q3 + 1.5 × IQR = 24 + 1.5 × 11.5 = 41.25
No value is less than -4.25 or greater than 41.25, therefore, there is no outlier in City B.
Learn more about the five-number summary on:
https://brainly.com/question/24809873
#SPJ1
a chart that compares three set of values in a three-dimensional chart is _____.
Answers
A chart that compares three sets of values in a three-dimension chart is called surface.
A two-dimensional collection of points (flat surface), a three-dimensional collection of points with a curved cross section (curved surface), or the perimeter of any three-dimensional solid are all examples of surfaces in geometry.
A surface is typically a continuous boundary that separates two areas of a three-dimensional space. For instance, a sphere's surface divides its interior from its exterior, and a horizontal plane divides the half-planes above and below it. Despite the fact that regions they contain are three-dimensional and have a volume, surfaces are basically two-dimensional and have an area. Despite this, surfaces are frequently referred to by the names of the regions they surround. Differential geometry studies the characteristics of surfaces, particularly the concept of curvature.
You can learn more about 3D surface at
https://brainly.com/question/16012416
#SPJ4
Which ordered pairs are solutions to the inequality 2x + y > - 4?
Select each correct answer.
(-1, -1), (4, -12), (5, -12), (0, 1), (-3, 0)
Answers
Answer:
Which ordered pairs are solutions to the inequality 2x + y > - 4?
Select each correct answer.
(-1, -1), (4, -12), (5, -12), (0, 1), (-3, 0)
The correct answer is:
(4, -12)