Which of the following represents the distributive property?
2x+3 = 2(x+3)
2(x +3) = 2x +6
2x+3 = 3(x+2)
2(x+3) = x +6
Answers
Answer:
2(x+3)=2x+6
Step-by-step explanation:
Because You multiply 2*x and 2*3.
The X is a variable and it actually equals to 1. so it's basically 2*1
After you multiply 2*x and 2*3 you will get 2x+6
Have a nice day!
Related Questions
Q9. Your team wanted to explore the effects of lack of sleep among UMD students. You randomly assigned those who volunteered to two groups. You asked the treatment group to keep awake for 19 hours; after they could sleep as much as they wanted. You asked the control group to sleep as much as they wanted and whenever they wanted. You made sure at the start that both groups had roughly the same mean blood pressure on average and then you checked their blood pressure again after two days. Let µt be mean blood pressure at the end for the treatment group and µC for the control group. Theory that you have read predicts that sleep deprivation will lead in higher blood pressure, even two days later. To test this, you compute a 95% confidence interval for the difference µt - µC, which you found to be (3.5, 16.8). Which of the following is true based on this study? a. Your team should conclude that sleep deprivation raises blood pressure. b. The data provide no evidence that sleep deprivation raises blood pressure. c. The confidence interval is too wide for a valid comparison. d. Based on this study you can conclude a causal relationship between sleep deprivation and blood pressure, as well as generalize your conclusions to all UMD students. e. The data provide evidence that blood pressure causes sleep deprivation.
Answers
Based on the study, the team cannot conclude that sleep deprivation raises blood pressure (option b). The confidence interval (3.5, 16.8) indicates that there is a range of possible values for the difference between the mean blood pressure of the treatment group and the control group.
The confidence interval being wide does not invalidate the comparison (option c). A wide interval simply indicates a larger range of plausible values, which may result from variability within the data or a smaller sample size. It does not invalidate the validity of the comparison itself. However, it does highlight the uncertainty in estimating the true difference between the two groups.
It's important to note that this study alone does not establish a causal relationship between sleep deprivation and blood pressure (option d). While the theory suggests such a relationship, this particular study's results do not provide conclusive evidence for causation. Additionally, the generalization of the conclusions to all UMD students would require a more diverse and representative sample.
The true difference could be anywhere within that range. Since the interval includes zero, it suggests that there is no statistically significant difference between the two groups' mean blood pressure after two days. Therefore, the data do not provide sufficient evidence to support the theory that sleep deprivation leads to higher blood pressure.
Finally, the data do not support the idea that blood pressure causes sleep deprivation (option e). The study design does not focus on examining the causal direction in that manner, and the results do not provide evidence to support this hypothesis.
Learn more about interval here:
https://brainly.com/question/11051767
#SPJ11
In triangle PQR, the length of PQ is 5 inches and the length of PR is 9 inches. Give all the possible whole-number lengths of side QR.
Answers
Answer:
\(4<QR<14\)
5, 6, 7, 8, 9, 10, 11, 12, and 13.
Step-by-step explanation:
We can use the triangle inequality. By the triangle inequality, the sum of any two sides of a triangle must be greater than the remaining side.
In other words, the sum of the two shorter sides must be greater than the longest side.
We know that PQ is 5 and PR is 9.
For the first case, let's say that neither PQ nor PR is the longest side. Instead, QR is the longest side. Then their sum must be greater than QR. Thus:
\(5+9>QR\Rightarrow QR<14\)
However, for the second case, let's say that QR is not the longest side. In this case, PR will be the longest side. Therefore, QR plus PQ must be greater than PR:
\(QR+5>9\Rightarrow QR>4\)
Thus, we have a compound inequality:
\(4<QR<14\)
Therefore, the possible whole-number lengths of QR are:
5, 6, 7, 8, 9, 10, 11, 12, and 13.
How do you prove that -4+1=-3?
Answers
Answer:
-4+1=-3
Step-by-step explanation:
If you were to use a number line=
-4 -3 -2 -1 0 1 2 3
-------------------------------------------------
+1
On the number line, if you move 1 up from -4, it moves to -3
EASY 25 POINTS
IF YOU GET IT WRONG I WILL NOT MARK BRAINLYEST

Answers
Answer: minimum: free
maximum: infinite
Use 3 0 x2 dx = 9 to evaluate each definite integral without using the Fundamental Theorem of Calculus. (a) 3 −3 x2 dx (b) 0 −3 x2 dx (c) 3 0 −8x2 dx (d) 3 −3 5x2 dx
Answers
To evaluate each definite integral without using the Fundamental Theorem of Calculus.
Integrals -
(a) ∫(3 to -3) \(x^2 dx = 0\)
(b) ∫(0 to -3) \(x^2 dx = 9\)
(c) ∫(3 to 0) \(-8x^2 dx = -72\)
(d) ∫(3 to -3) \(5x^2 dx = 0\)
What is Integrals?
In mathematics, the integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise from combining infinitesimally small data. The process of finding integrals is called integration.
To evaluate the definite integrals without using the Fundamental Theorem of Calculus, we can make use of the given information:
∫(0 to x) \(x^2 dx = 9\)
(a) To evaluate the integral ∫(3 to -3) \(x^2 dx\):
We can rewrite this integral as the sum of two integrals: ∫(3 to 0) \(x^2 dx\) + ∫(0 to -3)\(x^2 dx.\)
Using the given information, we have:
∫(3 to 0) \(x^2 dx\) = -∫(0 to 3)\(x^2 dx\)\(x^2 dx\) = -9
∫(0 to -3) \(x^2 dx\) = 9
Thus, ∫(3 to -3) \(x^2 dx\) = ∫(3 to 0) \(x^2 dx\) + ∫(0 to -3) \(x^2 dx\) = -9 + 9 = 0.
(b) To evaluate the integral ∫(0 to -3) \(x^2 dx\):
We already have ∫(0 to -3) \(x^2 dx\) = 9.
(c) To evaluate the integral ∫(3 to 0) \(-8\)\(x^2 dx\):
Since the given information is in terms of positive values of x, we need to reverse the limits of integration and change the sign:
∫(3 to 0) \(-8x^2 dx\) = -∫(0 to 3) \(-8x^2 dx\) = -8 * ∫(0 to 3) \(x^2 dx\) = -8 * 9 = -72.
(d) To evaluate the integral ∫(3 to -3) \(5x^2 dx\):
Similar to part (a), we can split this integral into two parts:
∫(3 to 0) \(5x^2 dx\) + ∫(0 to -3) \(5x^2 dx\).
Using the given information, we have:
∫(3 to 0)\(5x^2 dx\) = -∫(0 to 3) \(5x^2 dx\) = -5 * 9 = -45
∫(0 to -3)\(5x^2 dx\) = 5 * 9 = 45
Thus, ∫(3 to -3) \(5x^2 dx\)= ∫(3 to 0) \(5x^2 dx\) \(5x^2 dx\) + ∫(0 to -3)\(5x^2 dx\) = -45 + 45 = 0.
Therefore:
(a) ∫(3 to -3) \(x^2 dx\) = 0
(b) ∫(0 to -3)\(x^2 dx\) = 9
(c) ∫(3 to 0) \(-8x^2 dx\) = -72
(d) ∫(3 to -3) \(5x^2 dx\) = 0
To learn more about Integrals from the given link
https://brainly.com/question/12231722
#SPJ4
PLEASE HELP ASAP. What rule do you think is used at the pizza store to decide the final cost of pies?
Total cost in
Number of
pies
dollars
1
13
2
23
3
33
5
53

Answers
Answer:
13 dollars for the first 10 for each additional one ( i think)
Step-by-step explanation:
Answer:
the answer is it is $10 for each one with an additional cost as $3 at the end
> Chapter 8 > Lesson 8. 3. 2 > Problem 8-70
Assume Figure A and Figure B, at right, are similar.
a. If the ratio of similarity is then what is the ratio of the perimeters of Figures A and B?
Answer (a):
b. If the perimeter of Figure A is p and the linear scale factor is r, what is the perimeter of Figure B?
Hint (b):
C. If the area of Figure A is a and the linear scale factor is r, what is the area of Figure B?
Hint (c):
How do I do this????
Answers
Two figures are similar if their corresponding sides are in proportion and their corresponding angles are equal. In this case, Figure A and Figure B are similar, with a similarity ratio of r.
a. The ratio of the perimeters of similar figures is equal to the ratio of their corresponding sides. Since Figure A and Figure B are similar with a ratio of r, the ratio of their perimeters is also r.
b. If the perimeter of Figure A is p and the linear scale factor is r, the perimeter of Figure B can be found by multiplying the perimeter of Figure A by the linear scale factor:
Perimeter of Figure B = p * r
c. The area of similar figures is equal to the square of the linear scale factor multiplied by the area of the original figure. So, if the area of Figure A is a and the linear scale factor is r, the area of Figure B can be calculated as:
Area of Figure B = a * r^2
These formulas can be used to find the ratios and calculate the perimeters and areas of similar figures. Make sure to substitute the appropriate values given in the problem to find the specific answers.
Learn more about angles from
https://brainly.com/question/25716982
#SPJ11
Solve using the FOIL method
1. (x - 2)(x + 8)
2. (x + 6)(x - 12)
3. (x + 9)(x + 4)
4. (x + 6)(x + 2)
5. (x + 6)(x + 9)
6. (x - 4)(x + 5)
7. (x + 3)(x - 3)
8. (x + 10)(x + 10)
9. (x - 3)(x + 12)
10. (x + 4)(x - 3)
11. (x + 5)(x + 2)
12. (x - 3)(x - 4)
13. (x + 8)(x - 8)
14. (x -6)(x+3)
15. (x + 1)(x - 5)
Answers
Using the FOIL method, the products are:
1. x² + 6x - 16
2. x² - 6x - 72
3. x² + 13x + 36
4. x² + 8x + 12
5. x² + 15x + 54
6. x² + x - 20
7. x² - 9
8. x² + 20x + 100
9. x² + 9x - 36
10. x² + x - 12
11. x² + 7x + 10
12. x² - 7x + 12
What is the FOIL Method?The FOIL method is an acronym that stands for "First, Outside, Inside, and Last". This method simply describes the order you use in multiplying the terms of a given expression, that is, you have to multiply first terms, then outside terms, then inside terms, then last terms. The final step is to combine like terms together to arrive at your final answer.
Therefore, using the FOIL method, we have the following products:
1. (x - 2)(x + 8)
x² + 8x -2x - 16
Combine like terms
x² + 6x - 16
2. (x + 6)(x - 12)
x² - 12x + 6x - 72
Combine like terms
x² - 6x - 72
3. (x + 9)(x + 4)
x² + 4x + 9x + 36
x² + 13x + 36
4. (x + 6)(x + 2)
x² + 2x + 6x + 12
Combine like terms
x² + 8x + 12
5. (x + 6)(x + 9)
x² + 9x + 6x + 54
Combine like terms
x² + 15x + 54
6. (x - 4)(x + 5)
x² + 5x - 4x - 20
x² + x - 20
7. (x + 3)(x - 3)
x² - 3x + 3x - 9
x² - 9
8. (x + 10)(x + 10)
x² + 10x + 10x + 100
x² + 20x + 100
9. (x - 3)(x + 12)
x² + 12x - 3x - 36
x² + 9x - 36
10. (x + 4)(x - 3)
x² - 3x + 4x - 12
x² + x - 12
11. (x + 5)(x + 2)
x² + 2x + 5x + 10
x² + 7x + 10
12. (x - 3)(x - 4)
x² - 4x - 3x + 12
x² - 7x + 12
Learn more about the FOIL method on:
https://brainly.com/question/4053601
#SPJ1
Item 11
A 10-foot ladder leans against a wall so that it is 6 feet high at the top. The ladder is moved so that the base of the ladder travels toward the wall twice the distance that the top of the ladder moves up. How much higher is the top of the ladder now? (Hint: Let 8−2x be the distance from the base of the ladder to the wall.)
Answers
Answer:
4 ft higher
Step-by-step explanation:
Since the ladder is 10 ft long and its top is 6 feet high(above the ground), we find the distance of its base from the wall since these three (the ladder, wall and ground) form a right angled triangle. Let d be the distance from the wall to the ladder.
So, by Pythagoras' theorem,
10² = 6² + d² (the length of the ladder is the hypotenuse side)
d² = 10² - 6²
d² = 100 - 36
d² = 64
d = √64
d = 8 ft
Since the ladder is moved so that the base of the ladder travels toward the wall twice the distance that the top of the ladder moves up.
Now, let x be the distance the top of the ladder is moved, the new height of top of the ladder is 6 + x. Since the base moves twice the distance the top of the ladder moves up, the new distance for our base is 8 - 2x(It reduces since it gets closer to the wall).
Now, applying Pythagoras' theorem to the ladder with these new lengths, we have
10² = (6 + x)² + (8 - 2x)²
Expanding the brackets, we have
100 = 36 + 12x + x² + 64 - 32x + 4x²
collecting like terms, we have
100 = 4x² + x² + 12x - 32x + 64 + 36
100 = 5x² - 20x + 100
Subtracting 100 from both sides, we have
100 - 100 = 5x² - 20x + 100 - 100
5x² - 20x = 0
Factorizing, we have
5x(x - 4) = 0
5x = 0 or x - 4 = 0
x = 0 or x = 4
The top of the ladder is thus 4 ft higher
please help me i am trying to get al over do work turned in

Answers
Answer:
expanding
commutative prop
factorisation
simplifying
Step-by-step explanation:
The distributive property states that a(b+c) is equal to ab+ac and (a+b)c is equal to ac+bc. The commutative property states that a+b=b+a.
solving by elimination
7x-y=19
2x-3y=19
Answers
Answer:
2x + y = -2, x + 2y = 2
4x + y - 2z = 0, 2x+ 3z = 9 , -6x - 2y + z = 0
x + y = 4 , x - y = 2
Step-by-step explanation:
Answer:
x=2 and y=−5
Step-by-step explanation:
Let's solve your system by elimination.
7x−y=19;2x−3y=19
Multiply the first equation by -3,and multiply the second equation by 1.
−3(7x−y=19)
1(2x−3y=19)
Becomes:
−21x+3y=−57
2x−3y=19
Add these equations to eliminate y:
−19x=−38
Then solve−19x=−38for x:
−19x=−38
(Divide both sides by -19)
x=2
Now that we've found x let's plug it back in to solve for y.
Write down an original equation:
7x−y=19
Substitute2forxin7x−y=19:
(7)(2)−y=19
−y+14=19(Simplify both sides of the equation)
−y+14+−14=19+−14(Add -14 to both sides)
−y=5
y=-5
I only need help with number 1 and 2

Answers
Answer:
1. 12
2. 8
Step-by-step explanation:
\PLEASE MARK BRAINLIEST IT WILL HELP SM
What is the classification of AABC with vertices A(0, 0), B(4, 3), and C(4, -3) by
its sides?
(A) equilateral
(B) isosceles
(C) scalene
(D) right
Answers
Check the picture below.
well, let's take a peek at the distances of each side.
\(~\hfill \stackrel{\textit{\large distance between 2 points}}{d = \sqrt{( x_2- x_1)^2 + ( y_2- y_1)^2}}~\hfill~ \\\\[-0.35em] ~\dotfill\\\\ A(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad B(\stackrel{x_2}{4}~,~\stackrel{y_2}{3}) ~\hfill AB=\sqrt{[ 4- 0]^2 + [ 3- 0]^2} \\\\\\ ~\hfill AB=\sqrt{25}\implies \boxed{AB=5} \\\\\\ B(\stackrel{x_1}{4}~,~\stackrel{y_1}{3})\qquad C(\stackrel{x_2}{4}~,~\stackrel{y_2}{-3}) ~\hfill BC=\sqrt{[ 4- 4]^2 + [ -3- 3]^2} \\\\\\ ~\hfill BC=\sqrt{36}\implies \boxed{BC=6}\)
\(C(\stackrel{x_1}{4}~,~\stackrel{y_1}{-3})\qquad A(\stackrel{x_2}{0}~,~\stackrel{y_2}{0}) ~\hfill CA=\sqrt{[ 0- 4]^2 + [ 0- (-3)]^2} \\\\\\ ~\hfill CA=\sqrt{25}\implies \boxed{CA=5} \\\\\\ \textit{so it's an \underline{isosceles triangle}}\)

←C=$● RATIOS, PROPORTIONS, AND PERCENTSFinding the principal, rate, or time of a simple interest loan or...https://www-awuExplanationAldo borrowed money from a credit union for 6 years and was charged simple interest at an annual rate of 8%. The total interest that he paid was $1920. Howmuch money did he borrow?If necessary, refer to the list of financial formulas.I need help with this problem.
Answers
To solve this problem, you can use the following formula for simple interest:
\(A=Prt,\)where P is the initial amount, r is the rate of interest in decimal form, and t is the time in years.
Substituting A=1920, r=0.08, t=6, and solving for P, you get:
\(\begin{gathered} 1920=P(0.08)(6), \\ P=\frac{1920}{0.08(6)}. \end{gathered}\)Simplifying, you get:
\(P=4000.\)Answer: \(\text{ \$4000.}\)What is the radius of the circle shown, given that point P is its center?
A)13.5 ft
B)27 ft
C)54.5 ft
D)729 ft. PLSSS HELP ASAP

Answers
The radius of the circle with point P as its center is 13.5 ft.
A circle is the locus of a point such that its distance from a fixed point is always constant (the same).
The diameter of a circle is a straight line segment that passes through the center of the circle and has endpoints on the circle.
The radius of a circle is half the diameter of the circle.
Given that the diameter of the circle is 27 ft. hence, the radius of the circle is:
Radius = Diameter / 2
Radius = 27 ft / 2 = 13.5 ft.
Hence the radius of the circle is 13.5 ft.
Find out more at: https://brainly.com/question/14866670
g assuming the traditional denominations of coins available in the usa, which function should be used to determine how many pennies are required if we want to minimize the overall number of coins in making change for value v?
Answers
To minimize the overall number of coins the value would be V mod (100 + 50 + 25 + 10 + 5) so option d is correct choice.
This function returns the remainder when the V value is divided by the total value of the largest coin denomination available (100) plus the four next largest coin denominations (50, 25, 10, 5). As a result, a number of changes that cannot be implemented using only the largest denominations of coins must be implemented using smaller denominations, including pennies.
A legitimate capability would consider the value of the various coin sections and use that data to decide the most effective method for rolling out the improvement with the fewest coins possible.
The capability would almost certainly include division and modulus activities to compute the remainder of the value of V when partitioned by the value of each coin group.
The result of the capability would be the number of pennies required to complete the exchange, as pennies are the smallest denomination of coin that anyone could hope to find.
To learn more about traditional denominations
https://brainly.com/question/13122424
#SPJ4
HELP ASAP WILL GIVE FIRST ANSWER BRAINLEIST
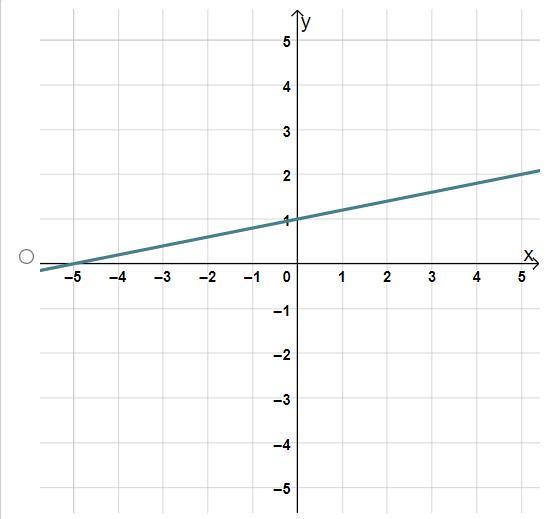
Which graph represents the linear equation y equals one fourth times x plus 1 on the coordinate plane?



Answers
Answer:
Below
Step-by-step explanation:
y= 1/4 x + 1
The graph has a y-axis intercept of +1 (y = mx + b form)
last one looks correct....at x = 4 the value is 2 which is correct
On a piece of paper, graph yz-2x-2. Then determine which answer choice
matches the graph you drew.
A
B
с
5
(-2,2)
(-2,2)
(-2,2)
(-2,2)
-5
0.-23
0.-27
(0.25
0.-235
-5
A. Graph D
B. Graph B
O C. Graph A
D. Graph C

Answers
Answer:B
Step-by-step explanation:
Option B is correct, the inequality y≥-2x-2 is represented in the second graph or graph B.
What is Graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points.
The given inequality is y≥-2x-2
y greater than or equal to minus two times of x minus two.
y≥-2x-2
The line passes through the points (-2, 2) and (0, -2).
As there is given greater than or equal to the line should be solid not dotted.
Greater than or equal to means we have to shade away from the origin.
The second graph satisfy all these properties.
y≥-2x-2 is represented in the second graph.
Hence, the inequality y≥-2x-2 is represented in the second graph.
To learn more on Graph click:
https://brainly.com/question/17267403
#SPJ7
A contractor builds homes of 12 different models and presently has 5 lots to build on. in how many different ways can he arrange homes on these lots? assume 5 different models will be built.
Answers
The number of different ways in which it can be built in the mentioned lots, using only five models as a reference is: 120.
What are Factorial Numbers?Factorial numbers are the products of all natural numbers before a particular number, it is usually represented with an exclamation mark at the end of the number (!) and they are usually used to represent the possible combinations of a certain number of elements.
In the case of the five models, this can be represented by 5! to identify the number of possible combinations that can be made with these five models, which are calculated as follows:
5! = 5 * 4 * 3 * 2 * 15! = 120Taking into account the calculation made, houses on the five lots can be arranged in 120 different ways.
If you want to learn more about Mathematics, you can visit the following link: https://brainly.com/question/17312578
#SPJ4
What is the answer to 2[5+2(8-6)]
Answers
Step-by-step explanation:
=2[5+2(8-6)]
=2[5+2(2)]
=2[5+4]
=2×9
=18
Answer: 18
Concept:
When encountering a question that needs to do operations with expressions, using the PEMDAS method will ease the process.
ParenthesesExponentsMultiplicationDivisionAdditionSubtractionSolve:
Given
2 [5 + 2 (8 - 6)]
Simplify values in the parentheses
=2 [5 + 2 × 2]
Simplify with multiplication
=2 [5 + 4]
Simplify the parentheses
=2 × 9
=18
Hope this helps!! :)
Please let me know if you have any questions
How many extraneous solutions does the equation below have?(2m)/(2m+3)-(2m)/(2m-3)=10123
Answers
Both solutions satisfy the original equation. As a result, there are no extraneous solutions in this case.
To determine the number of extraneous solutions in the given equation, let's simplify it step by step:
Step 1: Let's find the common denominator for the two fractions on the left side of the equation. The common denominator is (2m + 3)(2m - 3).
Step 2: Apply the common denominator to both fractions:
[(2m)(2m - 3)]/[(2m + 3)(2m - 3)] - [(2m)(2m + 3)]/[(2m + 3)(2m - 3)] = 1
Step 3: Simplify the numerators:
\([4m^2 - 6m - 4m^2 - 6m]/[(2m + 3)(2m - 3)] = 1\)
[-12m]/[(2m + 3)(2m - 3)] = 1
Step 4: Cancel out common factors:
-12m = (2m + 3)(2m - 3)
\(-12m = 4m^2 - 9\)
Step 5: Rearrange the equation:
\(4m^2 + 12m - 9 = 0\)
Step 6: Solve the quadratic equation using factoring, completing the square, or using the quadratic formula. Let's use the quadratic formula:
\(m = (-b ± √(b^2 - 4ac))/(2a)\)
For our equation, a = 4, b = 12, and c = -9. Substituting these values:
m = (-(12) ± √((12)^2 - 4(4)(-9)))/(2(4))
m = (-12 ± √(144 + 144))/(8)
m = (-12 ± √288)/8
m = (-12 ± 12√2)/8
Simplifying further:
m = (-3 ± 3√2)/2
So, we have two potential solutions for m:
m = (-3 + 3√2)/2 and m = (-3 - 3√2)/2
Now we need to check if these solutions satisfy the original equation. Let's substitute these values back into the equation:
For m = (-3 + 3√2)/2:
[(2(-3 + 3√2))/(2(-3 + 3√2) + 3)] - [(2(-3 + 3√2))/(2(-3 + 3√2) - 3)] = 1
Simplifying this equation, we find that it holds true.
For m = (-3 - 3√2)/2:
[(2(-3 - 3√2))/(2(-3 - 3√2) + 3)] - [(2(-3 - 3√2))/(2(-3 - 3√2) - 3)] = 1
Simplifying this equation, we also find that it holds true.
Therefore, both solutions satisfy the original equation. As a result, there are no extraneous solutions in this case.
To know more about solutions check the below link:
https://brainly.com/question/29174899
#SPJ4
Let U and V be independent random variables with means μ and variances σ2. Let Z = αU + V √ 1 − α2. Find E(Z) and rhoUZ.
Answers
The expected value of Z, E(Z), is αμ + μ * √(1 - α²).
The correlation coefficient between U and Z, ρUZ, is α.
These results provide insights into the relationship between the independent random variables U and V, and the newly defined random variable Z.
The expected value of a random variable represents the average value we would expect to obtain if we were to repeat the experiment many times. To find E(Z), we need to calculate the average value of Z.
We have Z = αU + V * √(1 - α²). Since U and V are independent, their expected values are simply their means, which are μ.
Now, let's calculate E(Z):
E(Z) = E(αU + V * √(1 - α²))
= αE(U) + E(V * √(1 - α²)) (by linearity of expectation)
= αμ + E(V) * √(1 - α²) (since E(U) = μ)
= αμ + μ * √(1 - α²) (since U and V have the same variance, their variances are both σ²)
Therefore, the expected value of Z, E(Z), is equal to αμ + μ * √(1 - α²).
Correlation coefficient between U and Z (ρUZ):
The correlation coefficient measures the linear relationship between two random variables. In this case, we want to find the correlation coefficient between U and Z, denoted as ρUZ.
The correlation coefficient ρUZ is defined as the covariance between U and Z divided by the product of their standard deviations.
To calculate ρUZ, we need to find the covariance between U and Z. The covariance between two random variables U and Z is given by:
Cov(U, Z) = E[(U - E(U))(Z - E(Z))]
Since U and V are independent, the covariance between U and V is zero. Therefore, we have:
Cov(U, Z) = Cov(U, αU + V * √(1 - α²))
= Cov(U, αU) + Cov(U, V * √(1 - α²))
= αCov(U, U) + 0
= αVar(U) (since Cov(U, U) = Var(U))
Using the given information that U has variance σ², we have:
Cov(U, Z) = ασ²
Next, let's calculate the standard deviations of U and Z.
Standard deviation of U (σU) = √(Var(U)) = √(σ²) = σ
Standard deviation of Z (σZ) = √(Var(Z))
= √(Var(αU + V * √(1 - α²)))
= √(α²Var(U) + Var(V * √(1 - α²))) (by independence)
= √(α²σ² + Var(V * √(1 - α²))) (since Var(U) = σ²)
= √(α²σ² + (1 - α²)Var(V)) (since Var(V * c) = c²Var(V), where c is a constant)
= √(α²σ² + (1 - α²)σ²) (since V has variance σ²)
= σ * √(α² + 1 - α²)
= σ * √(1)
Therefore, the standard deviation of Z, σZ, is equal to σ.
Now, we can calculate the correlation coefficient ρUZ:
ρUZ = Cov(U, Z) / (σU * σZ)
= ασ² / (σ * σ)
= α
Hence, the correlation coefficient between U and Z, ρUZ, is equal to α.
To know more about standard deviation here
https://brainly.com/question/16555520
#SPJ4
Find the area of the following shape. Use pi on your calculator when necessary.
9 mi
O 216 m²
O 108 m²
O 113.8 mi²
O 227.6 mi²
12 mi

Answers
The volume of the right cylinder is 1017.88 m² = 324π m²
One of the most fundamental curvilinear geometric shapes, a cylinder has traditionally been a three-dimensional solid. It is regarded as a prism with a circle as its base in basic geometry. In several contemporary fields of geometry and topology, a cylinder can alternatively be characterized as an infinitely curved surface.
The properties of cylinder are :
It features two flat circular faces, two curved edges, and one curved surface.
The two circular flat bases are parallel to one another.
There isn't a vertex on it.
The radius of a circular base and the height of a cylinder determine its size.
The radius of the cylinder = 6 m
Height = 9 m
The volume of the right cylinder is π(radius)²height
= π * 6² * 9 = 1017.88 m² = 324π m²
To learn more about Cylinder refer to :
brainly.com/question/28001461
#SPJ1
when using a graduated pipet, at which point do you measure the volume?
Answers
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
1. Place the graduated pipet on a flat surface and make sure it is level
2. Draw the liquid up until the meniscus is level with the etched line that corresponds to the desired volume
3. Make sure the liquid is not touching the etched line above it
4. Observe the bottom of the meniscus and take the reading at the point where the liquid level is between the two etched lines
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
6. bryce played the same song on guitar hero 8 times and scored the following percentages for his accuracy: 89%,82%,90%,88%,89%,91%,85%, and95% based on his scores, he wants to know the population mean that he will score a90%or better. which would be the best estimate? 0.5 0.625 0.25 0.375
Answers
The best estimate for the population mean that Bryce will score a 90% or better is 0.625.
Based on the given information, Bryce played the same song on Guitar Hero 8 times and scored percentages of 89%, 82%, 90%, 88%, 89%, 91%, 85%, and 95%. He wants to know the population mean that he will score a 90% or better. Which would be the best estimate?
To find the population mean, we need to calculate the average of Bryce's scores.
Step 1: Add up all the scores: 89 + 82 + 90 + 88 + 89 + 91 + 85 + 95 = 709.
Step 2: Divide the sum by the total number of scores (8): 709 / 8 = 88.625.
Therefore, the best estimate for the population mean that Bryce will score a 90% or better is 0.625.
To know more about population mean refer here:
https://brainly.com/question/33439013
#SPJ11
hey -
extra points for u *
what is 4 - 3?
what is 8 + 9?
what is 7 x 2?
goodbye now
Answers
Answer:
4-3=1
8+9=17
7 x 2= 14
Step-by-step explanation:
Answer:
1
17
14
Step-by-step explanation:
4 + -3 = 1
8 - -9=17
14/2=7
please i will give brainliest if right

Answers
Answer:
s = 156.25 square meters
Step-by-step explanation:
s = 2lw + 2lh + 2wh
s = 2(5.5)(3) + 2(3)(7.25) + 2(5.5)(7.25)
s = 33 + 43.5 + 79.75
s = 156.25 square meters
Answer:
We know,
\( \quad \)\({\boxed{ \rm{Surface \: Area_{ \: (rectangular \: prism)} = 2(lb + bh + hl)}}}\)
where,
Height (h) = 7.25mBreadth (b) = 3mLength (l) = 5.5m\( \: \)
\( {\longrightarrow { 2 ( 5.5 \times 3 + 3 \times 7.25 + 7.25 \times 5.5 ) }} \)
\( \longrightarrow \) 2 ( 16.5 + 21.75 + 39.875 )
\( \longrightarrow \) 2 ( 78.125 )
\( \longrightarrow \) 156.25
Thus, The Surface Area of rectangular prism is 156.25cm².
\( \rule{200pt}{2pt} \)
Additional Information:\(\footnotesize{\boxed{ \begin{array}{cc} \small\underline{ \sf{\pmb{ \blue{More \: Formula}}}} \\ \\ \bigstar \: \bf{CSA_{(cylinder)} = 2\pi \: rh}\\ \\ \bigstar \: \bf{Volume_{(cylinder)} = \pi {r}^{2} h}\\ \\ \bigstar \: \bf{TSA_{(cylinder)} = 2\pi \: r(r + h)}\\ \\ \bigstar \: \bf{CSA_{(cone)} = \pi \: r \: l}\\ \\ \bigstar \: \bf{TSA_{(cone)} = \pi \: r \: (l + r)}\\ \\ \bigstar \: \bf{Volume_{(sphere)} = \dfrac{4}{3}\pi {r}^{3} }\\ \\ \bigstar \: \bf{Volume_{(cube)} = {(side)}^{3} }\\ \\ \bigstar \: \bf{CSA_{(cube)} = 4 {(side)}^{2} }\\ \\ \bigstar \: \bf{TSA_{(cube)} = 6 {(side)}^{2} }\\ \\ \bigstar \: \bf{Volume_{(cuboid)} = lbh}\\ \\ \bigstar \: \bf{CSA_{(cuboid)} = 2(l + b)h}\\ \\ \bigstar \: \bf{TSA_{(cuboid)} = 2(lb +bh+hl )}\\ \: \end{array} }}\)
can someone help me with this

Answers
The area of the side of the cone is 100.53 cm² and the area of the cricle base is 50.27 cm² while the total surface area is 150.8 cm².
Understanding How to Solve Area of ConeFrom the diagram, we are given:
base radius (r) = 4cm
slant height (l) = 8cm
(a) To find the area of the side of the cone, we need to find the slant height and the base perimeter.
Using the Pythagorean theorem, we can find the height of the cone:
height = √(l² -r²)
= √(8² - 4²)
= √48
= 4√3 cm
The base perimeter is simply the circumference of the circle with radius 4 cm:
base perimeter = 2πr
= 2π(4)
= 8π cm
Now we can use the formula for the lateral surface area of a cone:
lateral surface area = 1/2 (base perimeter) (slant height)
= 1/2 (8π) (8)
= 32π cm²
= 100.53 cm²
Therefore, the area of the side of the cone is approximately 100.53 cm².
(b) The area of the circle base can be found using the formula:
base area = πr²
= π(4)²
= 16π cm²
= 50.27 cm²
Therefore, the area of the circle base is approximately 50.27 cm².
(c) The total surface area of the cone is the sum of the lateral surface area and the base area:
total surface area = lateral surface area + base area
= 32π + 16π
= 48π cm²
≈ 150.8 cm²
Therefore, the total surface area of the cone is approximately 150.8 cm².
Learn more about cone here:
https://brainly.com/question/30253224
#SPJ1
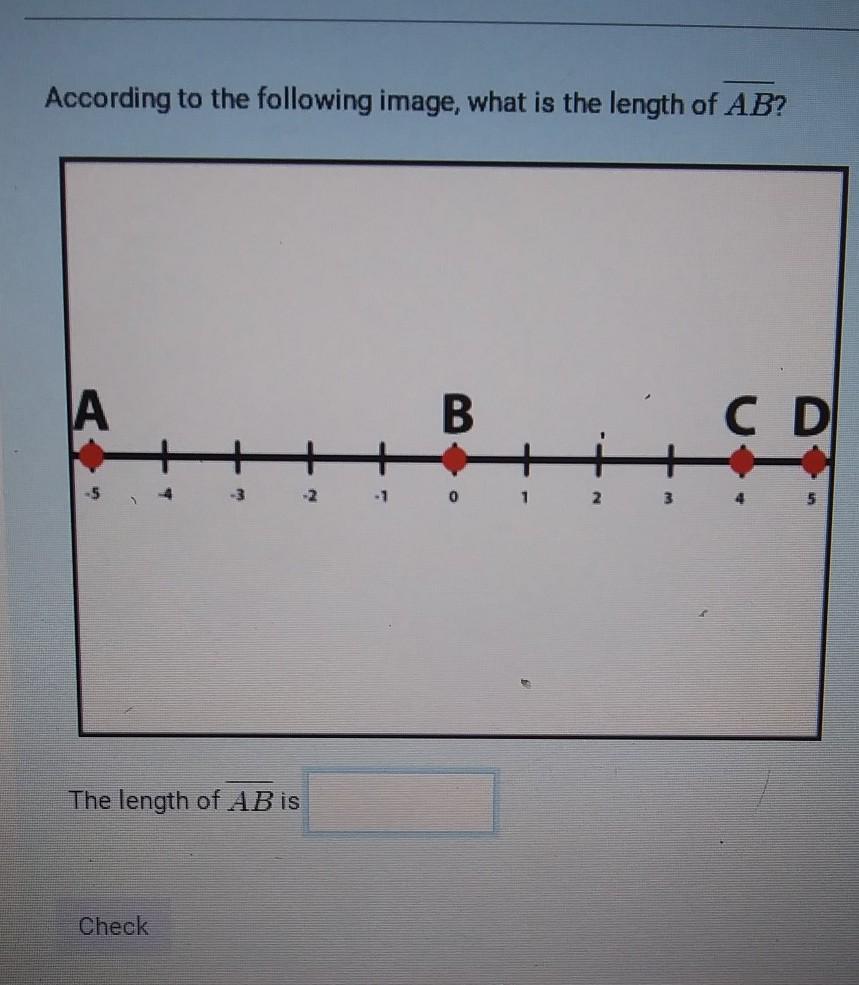
According to the following image, what is the length of AB?
Answers
Answer:
5
Step-by-step explanation:
The measure of the segment AB is 5 units.
Given that on a number line point A is at -5 and B is at 0 we need to find the measure of the segment AB,
To find the measure of the segment AB on a number line, we need to calculate the absolute difference between the coordinates of points A and B. In this case, point A is at -5, and point B is at 0.
The absolute difference between -5 and 0 is calculated as follows:
|(-5) - 0| = |-5| = 5
Therefore, the measure of the segment AB is 5 units.
Learn more about Absolute value click;
https://brainly.com/question/17360689
#SPJ2
you have a rectangle garden. the length is 5 more then twice the width. the perimeter is 100. how wide is the garden?
Answers
For the given algebraic expression, the value width is 15 units.
P = 2L + 2w (the perimeter is the two lengths and two widths put together) (the perimeter is the two lengths and two widths added together)
P = 100 (the perimeter is stated to be 100 feet).
L = 2w + 5 (length is 5 more than twice the width) (length is 5 more than twice the width)
Let's enter in some of the variable values we have now to see what results we have so far.
100 = 2(2w + 5) + 2w
Distribute 100 as follows: 4w + 10w + 2w
Rephrase: 100 = 6w + 10
You only need to separate w from here. Once you have that number, plug it into the equation L = 2w + 5 to determine the value of L, which will tell you the perimeter's length and breadth.
w = 100-10 / 6
w = 90/6
w = 15
To learn more about algebraic expression from given link
https://brainly.com/question/4344214
#SPJ9