Answers
Answer:
the third one
Step-by-step explanation:
v×k + 1/2v×9
v(k) + 1/2v (9)
Related Questions
30 POINTS!!!! What is the value of the y-coordinate of point A?

Answers
Answer:
0.65
Step-by-step explanation:
sin 15=0.65
Answer:
C
Step-by-step explanation:
the angle 15 is slanted on the lower left
Will give Brainliest and extra points if correct!!!
An experiment is conducted with a coin. The results of the coin being flipped twice 200 times is shown in the table.
Outcome Frequency
Heads, Heads 40
Heads, Tails 75
Tails, Tails 50
Tails, Heads 35
What is the P(No Heads)?
85%
75%
50%
25%
Answers
Answer:
To find the probability of getting no heads, we need to add the frequencies for the outcomes where tails appears twice and divide by the total number of trials:
No heads = Tails, Tails = 50
P(No Heads) = 50/200 = 0.25 = 25%
Therefore, the answer is 25%.
Answer:
The probability of getting no heads when flipping a coin twice is 25%.
The probability of getting heads on a single flip of a coin is 50%.
The probability of getting no heads when flipping a coin twice is:
```
(1 - 0.5)^2 = 0.25
```
Therefore, the probability of getting no heads when flipping a coin twice is 25%.
So the answer is 25%
Step-by-step explanation:
The box plots below show the math scores of students of two different classes, which statement is correct
Answers
Answer:
B
Step-by-step explanation:
Given the data:
Class A 55 72 75 89 95
Class B 55 70 75 94 100
CLASS A :
Minimum - 55
Lower quartile - 72
Median - 75
Upper quartile - 89
Maximum - 95
CLASS B :
Minimum - 55
Lower quartile - 70
Median - 75
Upper quartile - 94
Maximum - 100
Evaluating the statements given :
The median score of Class A is greater than the median score of Class B.
Median A = 75 ; Median B = 75 (median are equal), hence, A is not true
The lower quartile of Class A is greater than the lower quartile of Class B.
Lower quartile A = 72 ; Lower quartile B = 70 (A is greater than B) , hence, B is true
The upper quartile of Class A is greater than the upper quartile of Class B.
Upper quartile A = 89 ; Upper quartile B = 94 (A is less than B) , hence, statement is not true
The maximum score of Class A is greater than the maximum score of Class B.
Maximum A = 94 ; maximum B = 100 ; A < B ; Hence, statement is not true
Just need help on these two questions please

Answers
Using the standard normal distribution table, we can find the z-score corresponding to Lorena's score:
z = (x - μ) / σ = (554 - 495) / 20 = 2.95
Looking up the z-score of 2.95 in the standard normal distribution table, we find that the area to the left of this z-score is 0.9985.
Therefore, Lorena scored better than approximately 99.9% of the test takers, which we round to one decimal place as 99.9%.
On the 8th question, Given that the prices of bicycles are normally distributed with a mean (μ) of $208 and a standard deviation (σ) of $8, we need to find the percentage of bicycles priced greater than $203.
First, we need to calculate the z-score using the formula:
z = (X - μ) / σ
where X is the value we want to find the percentage for.
z = (203 - 208) / 8 = -0.625
Using a standard normal distribution table or calculator, we can find that the percentage of bicycles priced greater than $203 is 73.4% (rounded to one decimal place).
Therefore, approximately 73.4% of bicycles are priced greater than $203.
The area of a parallelogram is 240 in. If the base is 15 inches, find the height.
Answers
Answer:
The height would be 16 hope this helps:)!!!
The area of a parallelogram is the length x the height.
You are given the area and the length.
To find the height divide the area by the length.
Height = 240/15 = 16 inches.
Name
Fill in the blank to make the statement true.
1 3/4 + 1/6 +_____=7 1/2
Answers
Answer:
5
Step-by-step explanation:
For this question it is best to find the least common denominator (LCD) for all terms. In this case that denominator is 12.
Using the LCD you would convert all of the fractions into the following equation and solve:
1 9/12 + 2/16 + __ = 7 6/12
1 11/12 + __ = 7 6/12
___ = 7 6/12 - 1 11/12
___ = 5 7/12
Triangles DEF and D'E'F' are shown on the coordinate plane below: H F D D' 2 -8-7--5-4-3-2-1 1 2 3 4 5 6 7 8 T 20 F CO What rotation was applied to triangle DEF to create triangle D'E'F'?
Answers
No
Picture of coordinates (5,4) (3,4)
On a Cartesian plan
Answers
Both the coordinate points are plotted on the graph. The cartesian graph is attached with the answer.
What are coordinates?Coordinates are numbers which determine the position of a point or a shape in a particular space (a map or a graph). In the cartesian coordinate system, the coordinates are of the form (x, y).Other coordinate systems are : cylindrical and spherical coordinate systemGiven are the two coordinates to be plotted on a Cartesian plan -
(5, 4) , (3, 4).
The two given coordinate points are (5, 4) , (3, 4).
Refer to the graph attached. It shows both the points plotted.
Therefore, both the coordinate points are plotted on the cartesian graph.
To solve more questions on coordinates plotting and graphs, visit the link below -
https://brainly.com/question/24952385
#SPJ1

what is 12 wholes 1/4 Minus 9 wholes 3/4
Answers
Given:
12 wholes 1/4 Minus 9 wholes 3/4
The exponential function h whose graph is given below, can be written as h(x)=a*b^x Complete the equation for h(x)

Answers
Answer:
h(x) = 3*2^xStep-by-step explanation:
Given
Equation h(x)=a*b^x and its graphTwo points given on the graph:
h(0) = 3 and h(1) = 6Substitute the coordinates and simplify:
ab^0 = 3 ⇒ a = 3ab^1 = 6 ⇒ ab = 6Divide the second equation by the first to find the value of b:
b = 6/3 = 2The equation is:
h(x) = 3*2^xAnswer:
h(x) = 3*2^x
Step-by-step explanation:
The length of a rectangle is six times its width. If the perimeter of the rectangle is 70 cm, find its length and width.
length:
width:
Answers
Answer:
Step-by-step explanation:
Let's start by using the formula for the perimeter of a rectangle:
P = 2L + 2W
where P is the perimeter, L is the length, and W is the width.
We are given that the perimeter is 70 cm, so we can substitute this in the formula:
70 = 2L + 2W
Dividing both sides by 2, we get:
35 = L + W
We are also given that the length is six times the width, so we can write:
L = 6W
Substituting this in the equation we just derived, we get:
35 = 6W + W
Simplifying, we get:
35 = 7W
Dividing both sides by 7, we get:
W = 5
So the width of the rectangle is 5 cm.
Using the equation L = 6W, we can find the length:
L = 6 x 5 = 30
So the length of the rectangle is 30 cm.
Therefore, the length of the rectangle is 30 cm and the width is 5 cm.
Please answer this problem!

Answers
Answer:
a. volume= 784 is the answer
5. Solve the system of equations.
x + y = 6
2x - y = 9
Answers
x + y = 6
+
2x - y = 9
——————
3x = 15
x = 5
then just substitute that into one of the equations
(5) + y = 6
y = 1
then make into an ordered pair (x,y)
(5, 1)
For Field Day, the 72 students in fourth grade will be divided into tears with the same number of students on each team. The 60 students in third grade will be divided into teams that each have the same number of students as the fourth grade teams. What is the largest number of students that a team could have? Help meeee
Answers
We do this because the factors are the numbers determining the number of people and the number of teams, for example if they used the factors 6 and 10 for 60, they would make 6 teams of 10 people. And since factors are whole numbers, it makes sense for people and doesn’t cut ppl in half.
So the greatest factor that 72 and 60 gave have in common is 12, bc 5 x 12 is 60 and 6 x 12 is 72, and they don’t have other factors in common that are higher than 12.
This means that 12 is the answer, bc it’s the largest number of students that a team could have, in both the fourth and third grades.
how many points need to be removed from this graph so that it will be a function?
1 point
2 point
3 points
0 points

Answers
The number of points to be removed from the graph is 2
How many points to be removed from the graphfrom the question, we have the following parameters that can be used in our computation:
The graph
From the graph, we can see that
2 points have the same y coordinates
Another 2 points have the same y coordinates
For it to be a function, one of the 2 points must be removed each
So, we have the number of points to be removed from the graph is 2
Read more about functions at
https://brainly.com/question/27915724
#SPJ1
An inflatable ball can be modeled as a hollow sphere. Jace measures the outer diameter of the ball to be 50 cm. If the material that makes up the ball has a thickness of 1 cm, find the total volume of material that makes up the ball. Round your answer to the nearest hundredth if necessary. (Note: diagram is not drawn to scale.)

Answers
we have that
The volume of a sphere is given by the formula
\(V=\frac{4}{3}*pi*r^3\)The interior diameter is equal to
D=50-2(1)=48 cm
r=48/2=24 cm
The volume is equal to the volume of the sphere with the outer diameter minus the volume of the sphere with the interior diameter
so
\(\begin{gathered} V=\frac{4}{3}*pi*[25^3-24^3] \\ V=7,544.01\text{ cm}^3 \end{gathered}\)The volume is 7,544.01 cm3Help help ASAP please math nath

Answers
First, let's identify what r and h are from the equation by looking at the diagram of the cone
_______________
**Remember, r is the radius of a circle .... In the diagram, all we see is the diameter of the circle at the top of the cone. This is okay because radius is half of the diameter. The Diameter is 2
r = 1
Now h is the height of the cone. The diagram shows up that ...
h = 5
*Now let's plug in what we know into the equation they give us
V = πr²h / 3
*The instructions told us we can use "3" for π
V = 3(1)²(5) / 3
* quick tip! We see that the top AND bottom of the fraction both have the number 3, so we can cancel it out. (but you don't have to do this and you can work out the problem normally. We will still get the same answer) BUT, If we do cancel it out, now we are left with ...
V = (1)²(5)
1² = 1
so... V = 1 × 5
The volume of the cone is 5cm³
The median weekly income for a student who drops out of high school is 451. Someone with a bachelor's degree from college earns 1053 in that same week. Calculate each person's yearly income and then the difference between them.
Answers
The difference between their yearly incomes is $31,304.
To calculate each person's yearly income, we need to multiply their weekly income by the number of weeks in a year. Assuming there are 52 weeks in a year, the yearly income can be calculated as follows:
For the student who drops out of high school:
Yearly Income = Weekly Income x Number of Weeks
= 451 x 52
= 23,452
For someone with a bachelor's degree:
Yearly Income = Weekly Income x Number of Weeks
= 1053 x 52
= 54,756
The difference between their yearly incomes can be found by subtracting the student's yearly income from the bachelor's degree holder's yearly income:
Difference = Bachelor's Yearly Income - Student's Yearly Income
= 54,756 - 23,452
= 31,304
Therefore, the difference between their yearly incomes is $31,304.
It is important to note that these calculations are based on the given information and assumptions. The actual yearly incomes may vary depending on factors such as work hours, additional income sources, deductions, and other financial considerations.
Additionally, it is worth considering that educational attainment is just one factor that can influence income, and there are other variables such as experience, job type, and market conditions that may also impact individuals' earnings.
For more such answers on incomes
https://brainly.com/question/28414951
#SPJ8
help me please? i needa help. am bad at maths.

Answers
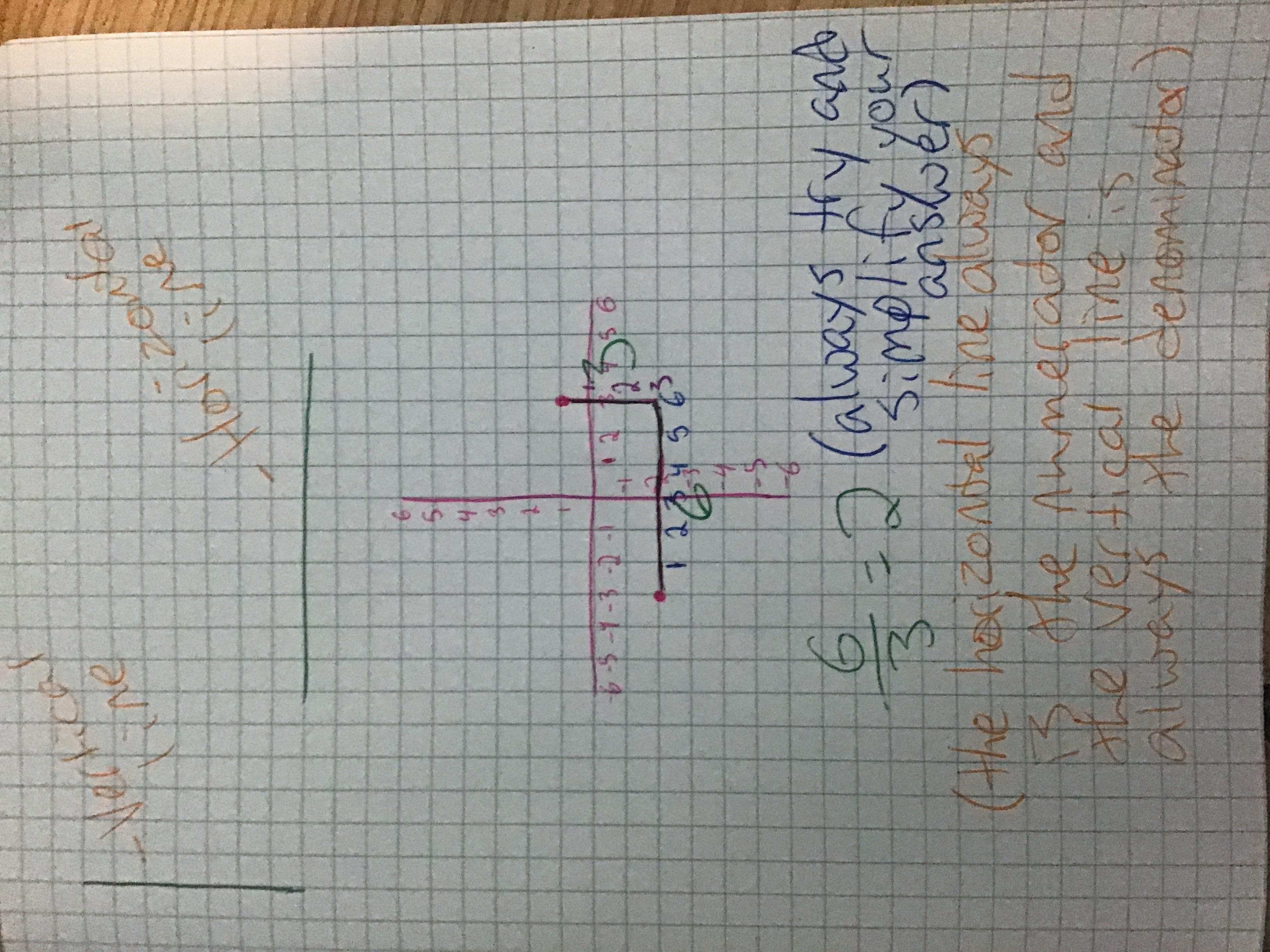
Answer:
6/3 or 2 (you should probably write 2 though)
(there’s a couple notes in the pic too that will help you with slopes)
Find the: x and y intercepts, asymptotes, x-coordinates of the critical points, open intervals where the function is increasing and decreasing, -coordinates of the inflection points, open intervals where the function is concave up and concave down, and relative minima and maxima. Using this information, sketch the graph of the function.
SHOW STEPS

Answers
The function has a relative minimum at (-1.278, -0.509) and a relative maximum at (1.278, 2.509).
How to find x-intercepts?
To find the x-intercepts, we set y = 0 and solve for x:
(x⁴/4) - x² + 1 = 0
This is a fourth-degree polynomial equation, which is difficult to solve analytically. However, we can use a graphing calculator or software to find the approximate x-intercepts, which are approximately -1.278 and 1.278.
To find the y-intercept, we set x = 0:
y = (0/4) - 0² + 1 = 1
So the y-intercept is (0, 1).
To find the vertical asymptotes, we set the denominator of any fraction in the function equal to zero. There are no denominators in this function, so there are no vertical asymptotes.
To find the horizontal asymptote, we look at the end behavior of the function as x approaches positive or negative infinity. The term x^4 grows faster than x^2, so as x approaches positive or negative infinity, the function grows without bound. Therefore, there is no horizontal asymptote.
To find the critical points, we take the derivative of the function and set it equal to zero:
y' = x³- 2x
x(x² - 2) = 0
x = 0 or x = sqrt(2) or x = -sqrt(2)
These are the critical points.
To determine the intervals where the function is increasing and decreasing, we can use a sign chart or the first derivative test. The first derivative test states that if the derivative of a function is positive on an interval, then the function is increasing on that interval. If the derivative is negative on an interval, then the function is decreasing on that interval. If the derivative is zero at a point, then that point is a critical point, and the function may have a relative maximum or minimum there.
Using the critical points, we can divide the real number line into four intervals: (-infinity, -sqrt(2)), (-sqrt(2), 0), (0, sqrt(2)), and (sqrt(2), infinity).
We can evaluate the sign of the derivative on each interval to determine whether the function is increasing or decreasing:
Interval (-infinity, -sqrt(2)):
Choose a test point in this interval, say x = -3. Substituting into y', we get y'(-3) = (-3)³ - 2(-3) = -15, which is negative. Therefore, the function is decreasing on this interval.
Interval (-sqrt(2), 0):
Choose a test point in this interval, say x = -1. Substituting into y', we get y'(-1) = (-1)³ - 2(-1) = 3, which is positive. Therefore, the function is increasing on this interval.
Interval (0, sqrt(2)):
Choose a test point in this interval, say x = 1. Substituting into y', we get y'(1) = (1)³ - 2(1) = -1, which is negative. Therefore, the function is decreasing on this interval.
Interval (sqrt(2), infinity):
Choose a test point in this interval, say x = 3. Substituting into y', we get y'(3) = (3)³ - 2(3) = 25, which is positive. Therefore, the function is increasing on this interval.
Therefore, the function is decreasing on the intervals (-infinity, -sqrt(2)) and (0, sqrt(2)), and increasing on the intervals (-sqrt(2), 0) and (sqrt(2), infinity).
To find the inflection points, we take the second derivative of the function and set it equal to zero:
y'' = 3x² - 2
3x² - 2 = 0
x² = 2/3
x = sqrt(2/3) or x = -sqrt(2/3)
These are the inflection points.
To determine the intervals where the function is concave up and concave down, we can use a sign chart or the second derivative test.
Using the inflection points, we can divide the real number line into three intervals: (-infinity, -sqrt(2/3)), (-sqrt(2/3), sqrt(2/3)), and (sqrt(2/3), infinity).
We can evaluate the sign of the second derivative on each interval to determine whether the function is concave up or concave down:
Interval (-infinity, -sqrt(2/3)):
Choose a test point in this interval, say x = -1. Substituting into y'', we get y''(-1) = 3(-1)² - 2 = 1, which is positive. Therefore, the function is concave up on this interval.
Interval (-sqrt(2/3), sqrt(2/3)):
Choose a test point in this interval, say x = 0. Substituting into y'', we get y''(0) = 3(0)² - 2 = -2, which is negative. Therefore, the function is concave down on this interval.
Interval (sqrt(2/3), infinity):
Choose a test point in this interval, say x = 1. Substituting into y'', we get y''(1) = 3(1)²- 2 = 1, which is positive. Therefore, the function is concave up on this interval.
Therefore, the function is concave up on the interval (-infinity, -sqrt(2/3)) and (sqrt(2/3), infinity), and concave down on the interval (-sqrt(2/3), sqrt(2/3)).
To find the relative extrema, we can evaluate the function at the critical points and the endpoints of the intervals:
y(-sqrt(2)) ≈ 2.828, y(0) = 1, y(sqrt(2)) ≈ 2.828, y(-1.278) ≈ -0.509, y(1.278) ≈ 2.509
Therefore, the function has a relative minimum at (-1.278, -0.509) and a relative maximum at (1.278, 2.509).
To know more about equations visit :-
https://brainly.com/question/22688504
#SPJ1
Enter the unknown value that makes this statement true:
20% of _ is 40.
Answers
Answer:
50
Step-by-step explanation:
0.8 * x = 40
40/0.8=50
Find function f(x) such that f(2x+1)=4x2 + 14x +7.
Answers
Answer: f=7 x=5
Step-by-step explanation:
I’m not sure because I solved on paper
help pls what is 4.05 × 0.8
Answers
Answer:
3.24
Step-by-step explanation:
character requirement
Answer:
3.24
Step-by-step explanation:
You could have used a calculator my dude. XD
1.
Use the formula d = rt. Find t for r = 39.5 m/h and d = 402.9 m.
15,915 h
0.1 h
10.2 h
363.4 h
Answers
What is the least common multiple of 3 and 16?
Answers
Need help with proofs, anyone know how?

Answers
Segments MS and QS are therefore congruent by the definition of bisector. Therefore, the correct answer option is: D. MS and QS.
What is a perpendicular bisector?In Mathematics and Geometry, a perpendicular bisector is a line, segment, or ray that bisects or divides a line segment exactly into two (2) equal halves and forms an angle that has a magnitude of 90 degrees at the point of intersection.
This ultimately implies that, a perpendicular bisector bisects a line segment exactly into two (2) equal halves, in order to form a right angle that has a magnitude of 90 degrees at the point of intersection.
Since line segment NS is a perpendicular bisector of isosceles triangle MNQ, we can logically deduce the following congruent relationships;
MS ≅ QSNS ≅ RSMN ≅ QN ∠NMS and ∠NQSΔMNS ≅ ΔQNSRead more on perpendicular bisectors here: brainly.com/question/19154899
#SPJ1
Complete Question:
The proof that ΔMNS ≅ ΔQNS is shown. Given: ΔMNQ is isosceles with base MQ, and NR and MQ bisect each other at S. Prove: ΔMNS ≅ ΔQNS
We know that ΔMNQ is isosceles with base MQ. So, MN ≅ QN by the definition of isosceles triangle. The base angles of the isosceles triangle, ∠NMS and ∠NQS, are congruent by the isosceles triangle theorem. It is also given that NR and MQ bisect each other at S. Segments _____ are therefore congruent by the definition of bisector. Thus, ΔMNS ≅ ΔQNS by SAS.
NS and NS
NS and RS
MS and RS
MS and QS
You only have 30 hours of vacation time left I always work 8 hours per day so that means that I can take ___ days off
Answers
Answer:
3
Step-by-step explanation:
If he always works 8 hours per day then he can take 3.75 days off.
What is division?Division is a mathematical operation, in which we distribute the number in equal parts, the number on the upper side is the total quantity and the number on the bottom side is equal parts of numbers which have to be distributed.
We denote division by '÷' this symbol.
Given that,
He has only have 30 hours of vacation time left,
Working time = 8 hours/day
Days off = ?
If he has 30 hours of vacation time left and you work 8 hours per day, you can take the following number of days off:
= 30 hours/8 hours per day
= 3.75 days
So, you can take 3.75 days off, which is equivalent to 3 full days and 12 hours.
To know more about division check:
https://brainly.com/question/21416852
#SPJ5
PLEASE HELP ON QUESTION ASAP !
Hi please help on question.If you get answer correct is be willing to give brainliest,a thanks, five stars and 10pts.
My question:
As an analogy of a circuit with resistance, think of an obstacle race . Which parts of a circuit do the obstacles represent? which part of the circuit do the people respresent?
Answers
The electric current to flow through the resistors and complete the circuit by reaching its intended destination or powering a device.
In the analogy of a circuit with resistance, we can compare it to an obstacle race. Here's how we can relate the different elements:
Circuit: The entire obstacle race course represents the circuit itself. It includes all the components and paths that the participants will go through.
Obstacles: The obstacles in the race represent the resistors in the circuit. Just like resistors impede the flow of electrical current in a circuit, obstacles in the race impede the progress of the participants.
People/Participants: The people participating in the race represent the flow of electric current in the circuit. They are the "charge" moving through the circuit, encountering and overcoming obstacles (resistors) to reach the finish line.
The goal of the participants (people) is to navigate through the obstacles (resistors) and complete the race (circuit) by reaching the finish line.
Similarly, in an electrical circuit, the goal is for the electric current to flow through the resistors and complete the circuit by reaching its intended destination or powering a device.
Learn more about analogy problem here:
https://brainly.com/question/13440226
#SPJ1
Please answer this before friday
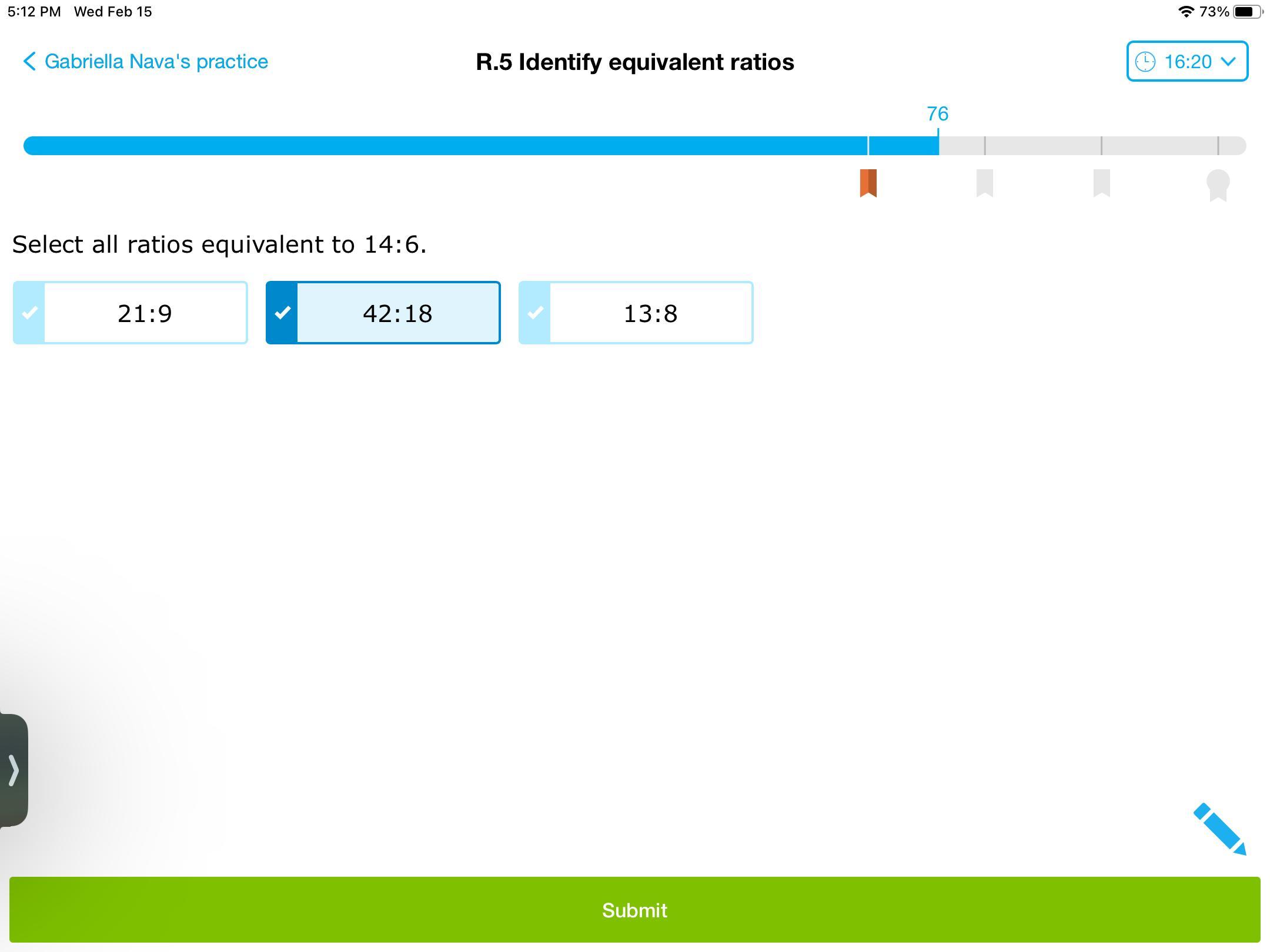
Answers
Answer: 21:9 and 42:18
Step-by-step explanation:
14:6 at its most basic form is 7:3, so find anything that could be equal to this if a number is multiplied on both sides.
21:9 is our simplified ratio multiplied by 3 on both sides.
42:18 is our simplified ratio multiplied by 6 on both sides.
But, the final ratio doesn't work, because 7 and 3 respectively cannot multiply to 13 and 8 with the same value.
Who can solve this for me real quick?

Answers
Answer:
Vertex (-3, -3)
Step-by-step explanation:
Highest or lowest point lying on the graph of a parabola is said to be the Vertex of a parabola.
By this definition, point P (lowest point) is the vertex of the given parabola.
Coordinates of the Vertex are (-3, -3).
Therefore, Vertex (-3, -3) is the answer.

