Which statement is true about the lengths of the sides?
Each side has a different length,
Two sides have the same length, which is less than
the length of the third side.
The three sides have the same length.
The sum of the lengths of two sides is equal to the
length of the third side.
Answers
Answer:
The three sides have the same length.
Step-by-step explanation:
Answer:
B. Two sides have the same length, which is less than the length of the third side.
Step-by-step explanation:
I think, :-P
Related Questions
The length of a colorado brook trout is normally distribute. what is the probability that a brook trout's length exceeds the mean? (round your answer to 2 decimal places.) the likelihood of a value greater than the mean is .50 because the whole area under the curve is 1 and the mean is the midway point.
Answers
The probability that a brook trout's length exceeds the mean is 0.50.
How to find the probability in normal distribution?One of the benefits of normal distributions is that we can find probabilities without being given the parameters of the distribution. This is achieved provided that we know the number of standard deviations from the mean the value of the random variable that delimits the indicated interval is.
We are given;
Distribution of length of a Colorado brook trout; Normal Distribution
Now, we want to find the likelihood of a value greater than the mean is 0.50.
We also know that if it is seen that the shape of the data is almost like a bell shape, then the data will be considered to have a normal distribution.
Thus, by the property of a normal distribution, the probability is 0.50.
Read more about probability in normal distribution at; https://brainly.com/question/4079902
#SPJ1
The corner Deli operates on an overhead percent of 20% of the selling price, which results on an overhead of $1.25 on the company's private-labeled bags of corn chips. If the corner Deli has a markup of $4.35 on the bag of corn chips, find (a) selling price, (b) net profit, and (c) cost.
Answers
a) The Selling price at a markup of $4.35 on the bag of corn chips is $6.25 b) The Net profit a markup of $4.35 on the bag of corn chips is $3.10 c) The cost at a markup of $4.35 on the bag of corn chips is $1.90.
How to find selling price,net profit, and cost.We can use the following equations to solve for the selling price, net profit, and cost of the corn chips:
(a) Selling price = cost + markup
(b) Net profit = selling price - cost - overhead
(c) Overhead = overhead percent x selling price
Given that the overhead is $1.25 and the overhead percent is 20%, we can calculate the selling price as follows:
Now that we know the selling price, we can use equation (a) to calculate the cost:
(a) Selling price = cost + markup
$6.25 = cost + $4.35
Cost = $6.25 - $4.35
Cost = $1.90
(b) Net profit = selling price - cost - overhead
Net profit = $6.25 - $1.90 - $1.25
Net profit = $3.10
(c) Overhead = overhead percent x selling price
$1.25 = 0.2 x selling price
Selling price = $1.25 / 0.2
Selling price = $6.25
Therefore, the selling price of the corn chips is $6.25, the net profit per bag is $3.10, and the cost is $1.90.
Learn more about Net profit at https://brainly.com/question/28390284
#SPJ1
A charge of −3.10nC is placed at the origin of an xy-coordinate system, and a charge of 1.90nC is placed on the y axis at y=4.50 cm. If a third charge, of 5.00nC, is now placed at the point x=2.65 cm,y=4.50 cm find the x and y components of the total force exerted on this charge by the other two charges. Enter your answers in newtons separated by a comma. Part B Find the magnitude of this force. Express your answer in newtons. Find the direction of this force. Express your answer in degrees.
Answers
The x and y components of the force are -3.10 x 10⁻⁵ N and 2.82 x 10⁻⁵ N, respectively.
The magnitude of the force is 3.96 x 10⁻⁵ N, and the direction of the force is -41.6 degrees.
Now, we can use Coulomb's law, which tells us that the force between two charges is given by:
F = k (q₁ q₂) / r²
where F is the force, k is Coulomb's constant (9.0 x 10⁹ N*m²/C²), q₁ and q₂ are the charges, and r is the distance between the two charges.
For the first charge at the origin and the third charge at (2.65 cm, 4.50 cm), the distance between them is:
r₁ = √((2.65 cm)² + (4.50 cm)²) = 5.23 cm
The direction of the force is along the line connecting the two charges and can be found using trigonometry:
θ₁ = tan⁻¹ (4.50 cm / 2.65 cm) = 59.0 degrees
The force exerted on the third charge by the first charge is then:
F₁ = (9.0 x 10⁹ Nm²/C²) (-3.10 nC) × (5.00 nC) / (5.23 cm)²
= -6.19 x 10⁻⁵ N
To find the x and y components of this force, we can use:
Fx1 = F₁ * cos(theta1) = -3.10 x 10⁻⁵ N
Fy1 = F₁ * sin(theta1) = -4.99 x 10⁻⁵ N
For the second charge on the y-axis and the third charge at (2.65 cm, 4.50 cm), the distance between them is:
r₂ = sqrt((2.65 cm)² + (4.50 cm - 4.50 cm)²) = 2.65 cm
The direction of the force is along the y-axis, so there is no x component. The y component of the force is:
Fy₂ = (9.0 x 10⁹ Nm²/C²) (1.90 nC) × (5.00 nC) / (2.65 cm)²
= 7.81 x 10⁻⁵ N
The total force on the third charge is the sum of the forces from the first and second charges:
Fx = Fx₁ + 0 = -3.10 x 10⁻⁵ N
Fy = Fy₁ + Fy₂ = 2.82 x 10⁻⁵ N
The magnitude of the force is:
F = √(Fx² + Fy²) = 3.96 x 10⁻⁵ N
The direction of the force is:
theta = tan⁻¹(Fy / Fx) = -41.6 degrees
(measured counterclockwise from the positive x-axis)
Therefore, the x and y components of the force are -3.10 x 10⁻⁵ N and 2.82 x 10⁻⁵ N, respectively.
The magnitude of the force is 3.96 x 10⁻⁵ N, and the direction of the force is -41.6 degrees.
Learn more about Coulomb's law visit:
https://brainly.com/question/506926
#SPJ4
Find the sum of the series.
[infinity] (−1)nπ2n
n=0
62n(2n)!
Answers
As per the Maclaurin series, the value of the function is written as 2.8521
The term Maclaurin series is defined as a function that has expansion series that gives the sum of derivatives of that function.
Here we have given that the function is \(\sum\frac{(-1)^n\pi^{2n}}{4^{2n}(2n)!}\)
And we need to find the sum of series by using the Maclaurin series as
Now, the sum of series is calculated as,
=>f(n) = \(\sum\frac{(-1)^n\pi^{2n}}{4^{2n}(2n)!}\)
When we put the value on n = 0, then we get,
=> f(0) = [1 x 3.14]/1] = 3.14
Now, we have to put the value of the function, the value of x as 1,
Then we get,
=> f(1) = [-1 x 9.8596] / [16 x 2]
=> f(1) = -0.308
And then we have to put the value of function for the value of x as 2,
Then we get,
=> f(2) = [1 x 30.959] / [64 x 24]
=> f(2) = 0.0201
Then the sum of the series is
=> 3.14 - 0.308 + 0.0201
=> 2.8521
To know more about function here.
https://brainly.com/question/28193995
#SPJ4
Please, Please, Please Help MEE!! ASAP!

Answers
1a. 35
b. 17.5
c. 3.5d
2. $4.5
We have an Hamiltonianstudent submitted image, transcription available belowwith the Eigenstatesstudent submitted image, transcription available belowand corresponding Eigenvaluesstudent submitted image, transcription available below. We have also a state
student submitted image, transcription available below.
Question: If we set up the system as
student submitted image, transcription available below
a) If we wait a timestudent submitted image, transcription available belowwhat is the probability that we getstudent submitted image, transcription available below?
b) If we saw that it was in the statestudent submitted image, transcription available belowthen after we wait for a timestudent submitted image, transcription available belowwhat is the probability that it is stillstudent submitted image, transcription available below?
c) If you do the measurements in short intervalls over and over again, what happens?
Answers
a) The probability of obtaining the state student submitted image after waiting a time student submitted image is given by the square of the corresponding coefficient in the state's expansion in terms of the eigenstates.
b) If the initial state is student submitted image and we wait for a time student submitted image, the probability of it remaining in the same state is given by the square of the absolute value of the corresponding coefficient in the state's expansion in terms of the eigenstates.
c) If measurements are performed repeatedly in short intervals, the system will collapse into one of the eigenstates with their associated probabilities, according to the principles of quantum mechanics.
a) To calculate the probability of obtaining the state student submitted image after waiting a time student submitted image, we need to express the state in terms of the eigenstates. The expansion coefficients in the state's expansion represent the probability amplitudes. The probability of obtaining a specific eigenstate is given by the square of its coefficient. Therefore, the probability of obtaining the state student submitted image is determined by squaring the corresponding coefficient in the state's expansion.
b) If the initial state is student submitted image and we wait for a time student submitted image, the state will evolve according to the time evolution operator. To find the probability of it remaining in the same state, we need to calculate the coefficient of the initial state in the evolved state after time student submitted image. The probability is then given by the square of the absolute value of this coefficient.
c) When measurements are performed repeatedly in short intervals, the system undergoes the process of wave function collapse. Each measurement projects the system onto one of the eigenstates with their associated probabilities. After each measurement, the state of the system is no longer in a superposition but rather in a definite eigenstate. Subsequent measurements will yield the same result with certainty, as the system remains in the collapsed state until another measurement disturbs it.
In summary, the probabilities in quantum mechanics are determined by the coefficients in the expansion of the state in terms of eigenstates. Waiting for a certain time leads to the evolution of the state, and the probability of remaining in the same state or transitioning to another state can be calculated. Repeated measurements cause the system to collapse into definite eigenstates, leading to consistent outcomes.
Learn more about Probability
brainly.com/question/31828911
#SPJ11
Alberto started out bench pressing 60 pounds. He then added 5 pounds every week. Determine whether the situation is linear or nonlinear, and proportional or nonproportional
Answers
Answer
linear
nonproportional
Step-by-step explanation:
Since for each equal change in time (1 week), there is an equal change in weight (5 lb), the situation is linear.
At time zero, the first week, the weight was not zero. It was 60 lb, so it is not proportional.
Answer:
linear
nonproportional
Mr. Jackson is ready to empty his backyard swimming pool for the winter. He knows that the time, T, required to empty the pool varies inversely as the rate, R, of pumping. Mr. Jackson's old pump could empty the pool in 55 minutes, pumping at a rate of 200 gallons per minute. This year he has a new pump which pumps at a rate of 325 gallons per minute. How long will it take to empty the pool this season? Round your answer to the nearest minute. DUE IN 2 HOURS, 15 POINTS, WILL GIVE BRAINLIEST.

Answers
Answer:
34 minutes
Step-by-step explanation:
Given that T varies inversely as R then the equation relating them is
T = \(\frac{k}{R}\) ← k is the constant of variation
To find k use the condition
T = 55 when R = 200, that is
55 = \(\frac{k}{200}\) ( multiply both sides by 200 )
11000 = k, thus
T = \(\frac{11000}{R}\) ← equation of variation
When R = 325, then
T = \(\frac{11000}{325}\) ≈ 34 minutes ( to the nearest minute )
Answer:
Option 2
Step-by-step explanation:
An inverse variation can be represented by the equation xy=k or y=kx .
If (x1,y1) and (x2,y2) are solutions of an inverse variation, then x1y1=k and x2y2=k
Substitute x1y1 for k
x1y1=x2y2 or x1x2=y2y1
The equation x1y1=x2y2 is called the product rule for inverse variations.
Let x be the time required, and y the rate of pumping.
x1 = 55min y1 = 200gal/min
x2 = Unknown y2 = 325gal/min
(55)(200) = x2(325)
11,000 = x2 (325)
11,000/325 = x2
33.84 = x2
34 minutes
Emilia and Rose ran around a track. Emilia ran 3 more laps than Rose. Altogether, they ran 11 laps.
How many laps did Rose run?
Answers
Please help for section d) 100 points, must show all working and step by step

Answers
Answer:
Step-by-step explanation:
(a) and (b) see diagram
(c) you can see from the graph, the purple line hits the parabola twice which is y=6 or k=6
(d) Solving simultaneously can mean to set equal
6x - x² = k >subtract k from both sides
6x - x² - k = 0 >put in standard form
- x² + 6x - k = 0 >divide both sides by a -1
x² - 6x + k = 0
(e) The new equation is the same as the original equation just flipped (see image)
(f) The discriminant is the part of the quadratic equation that is under the root. (not sure if they wanted the discriminant of new equation or orginal. I chose new)
discriminant formula = b² - 4ac
equation: x² - 6x + 6 = 0 a = 1 b=-6 c = 6
discriminant = b² - 4ac
discriminant= (-6)² - 4(1)(6)
discriminant = 36-24
discriminant = 12
Because the discriminant is positive, if you put it back in to the quadratic equation, you will get 2 real solutions.

Janet wants to invest a sum of money that will grow to $10,000 in 5 years. How much does she need to put now into an account that pays 4% interest per year, compounded monthly?
Answers
Janet needs to invest $8,164.86 now to have $10,000 in 5 years at a 4% annual interest rate, compounded monthly.
How to Calculate Compound Interest?To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
where A is the final amount, P is the initial amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
We want to find the initial amount, P, so we can rearrange the formula as follows:
P = A/(1 + r/n)^(nt)
Substituting the given values, we have:
A = $10,000
r = 4% = 0.04 (as a decimal)
n = 12 (monthly compounding)
t = 5 years
Therefore, the initial amount, P, is:
P = $10,000/(1 + 0.04/12)^(12*5)
= $8,164.86 (rounded to two decimal places)
Learn more about compound interest on:
https://brainly.com/question/24924853
#SPJ1
Answer:8,190
Step-by-step explanation:
Use the formula for present value:
PV = FV (1 +
)-nt
FV = $10,000
r = 0.04
n = 12
t = 5
PV = 10,000 (1 +
)12 · 5
= 8,190
Please help , I need help thanks
these are the questions there are five , I need this today
I will give out brainlist





Answers
The solution to the inequality problem is represent by the graph attached below.
Graph of InequalitiesTo solve this problem we simply need to use a graphing a calculator to plot the graph of the two inequalities. The points of intersection represents the solution of the graph.
The broken purple line represents the first inequality and the second straight line represents the second inequality.
Learn more on graph of inequalities here;
https://brainly.com/question/11234618
#SPJ1



if 2^6=y^3 what is y?
Answers

Answer:
y=4
Step-by-step explanation:
simplify 2^6 --> 64
find the cube root of 64,
y=4
(Q2) The set of line segments _____ meet the requirements to form a triangle.8 cm4 cm3 cm
Answers
To form a triangle, the set of line segments must satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Therefore, we need to check if the given line segments 8 cm, 4 cm, and 3 cm meet this requirement.
We can start by checking if the sum of the two smaller sides (3 cm and 4 cm) is greater than the largest side (8 cm). 3 cm + 4 cm = 7 cm, which is less than 8 cm. Therefore, these three line segments cannot form a triangle.
In general, for a set of line segments to form a triangle, the largest side must be smaller than the sum of the other two sides. In this case, the line segment of 8 cm is too long compared to the other two sides, which makes it impossible to form a triangle.
In conclusion, there are no line segments that meet the requirements to form a triangle with lengths of 8 cm, 4 cm, and 3 cm.
learn more about the inequality theorem here: brainly.com/question/1163433
#SPJ11
A jeweler has 20 ounces of a gold alloy worth $160 per ounce and 10 ounces of a silver alloy worth $140 per ounce. she has a third alloy that is worth $124 per ounce. how much of this third alloy must she combine with the other two to make 3-ounce pieces of jewelry worth $438 each?
Answers
The amount of ounces of the third alloy that will be used to make 3-ounce pieces of jewelry worth $438 is 1.1129 ounce
How to find the amount of the third alloyLet the first alloy be g
Let the second alloy be s
Let the third alloy be x
to get the amount of the third alloy that will have a combination worth $438
$160 + $140 + $x = $438
$300 + $x = $438
$x = $438 - $300
$x = $138
1 ounce of x is $124
? ounce = $138
cross multiplying
? * 124 = 138
? = 138 / 124
? = 1.1129 ounce of the third alloy will e required
Learn more about ounces in equation at:
https://brainly.com/question/19645621
#SPJ1
She combine with the other two to make 3-ounce pieces of jewelry worth $438 each is 0.75 ounces.
Let's define some variables:
g = ounces of gold per piece
s = ounces of silver per piece
x = ounces of other alloy per piece
There's twice as much gold as there is silver, so:
g = 2s
The total weight of the piece is 3 ounces, so:
g + s + x = 3
The total cost is $438, so:
160g + 140s + 124x = 438
Three equations, three variables. We can solve the system of equations. If we substitute the first equation into the second:
2s + s + x = 3
3s + x = 3
x = 3 − 3s
If we substitute this new equation and the first equation into the third equation:
160 (2s) + 140s + 124 (3 − 3s) = 438
320s + 140s + 372 − 372s = 438
88s = 66
s = 0.75
Now solve for g and x:
g = 2s = 1.5
x = 3 − 3s = 0.75
Therefore, the amount of alloy equals the amount of silver. The jeweler has 10 ounces of silver, so she needs 10 ounces of alloy.
HELP PLEASE 77 POINTS

Answers
Answer:
You find it by finding the dimensions of the X up and down, and Y left and right
Step-by-step explanation:
The volume of a hemisphere = (2/3)πr3 cubic units. Where π is a constant whose value is equal to 3.14 approximately. “r” is the radius of the hemisphere. volume of a cone is 1 3 π r 2 h \frac { 1 } { 3 } \pi r ^{ 2 } h 31πr2h, where r denotes the radius of the base of the cone, and h denotes the height of the cone. formula to find the volume of a hemisphere is 2TTr3 / 3, where pi is 3.14, and the radius is half of the diameter.
Since you have a width of 30 ft, I’m guessing 30 x 10 divided by half of 3.14. I hope this helped ! Please leave a brainliest mark and a thanks (:
Find each of the missing sides of the right triangles using Pythagorean Theorem.

Answers
We need to apply the Pythagorean Theorem, which says that the square of the Hypothenuse is equal to the sum of the squares of the cathetus. So we have:
\(\begin{gathered} 41^2=x^2+9^2 \\ 1681=x^2+81 \\ x^2=1681-81 \\ x^2=1600 \\ x=\sqrt[]{1600} \\ x=40 \end{gathered}\)The missing side is equal to 40.
Solve the equation
3(4z-7)=-21+12z
Answers
Answer:
Step-by-step explanation:
Let's open the brackets,
12z - 21 = -21 + 12z (distributive property)
12z - 12z = -21 + 21
0z = 0
z = 0
Ceiling Height: Suppose the ceiling of a home is 3.06 meters above the floor. Express the height of the ceiling in centimeters.The ceiling is ? centimeters tall.
Answers
One meter is equal to 100 centimeters.
Now, we need to know 3.06 meters in centimeters:
Use the rule of three to find this value
1meter-------------------- 100cm
3.06------------------------- x cm
Where x is = (3.06*100)/1
Then x=306
The ceiling is 306 centimeters tall.
use the given frequency distribution to find the (a) class width. (b) class midpoints of the first class. (c) class boundaries of the first class.
Answers
(a)The class width = 3
(b) The class midpoint of the first class = 51
(c) The class boundaries of the first class = (49.5, 52.5)
Consider the frequency distribution in the following image.
We know that in frequency distribution the class width is nothing but the distance between the lower limits of consecutive classes.
Whereas the range is the difference between the maximum and minimum data entries.
The smallest number is 50, and the largest is 62.
So the range is 62 - 50 = 12
We know that the formula for the class width:
Class width= upper limit – lower limit +1
So, the class width = 52 - 50 + 1
= 3
The formula for the midpoint of each class:
midpoint = (lower limit of class + upper limit of class)/2
Let us assume that m be the midpoint of the first class.
Using above formula of midpoint:
m = (50 + 52)/2
m = 51
We know that the class boundaries are nothing but the end points of an open interval which contains the class interval.
So, the class boundaries of the first class = (49.5, 52.5)
Learn more about the frequency distribution here:
https://brainly.com/question/14926605
#SPJ4

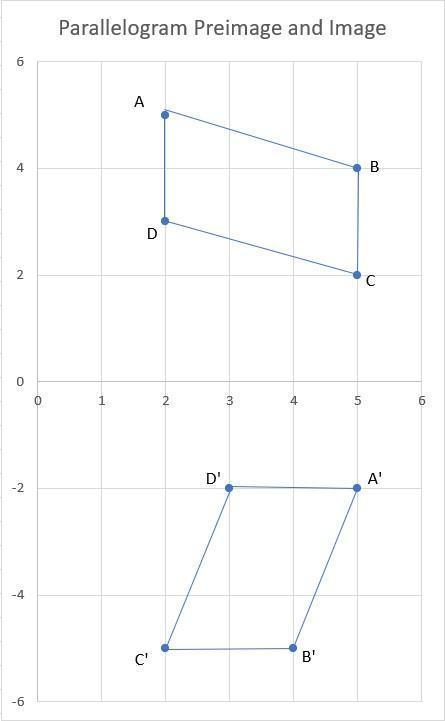
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Add. Write your answer as a fraction in simplest form. 6+(−4 3/4)+(−2 1/8)=
Answers
what assumption is necessary about the population distribution in order to perform a dependent means hypothesis test?
Answers
The assumption of the differences between the paired observations is necessary about the population distribution in order to perform a dependent means hypothesis test.
A dependent means hypothesis test, also known as paired or matched samples, must be conducted on the presumption that the population's differences between the paired observations are normally distributed. Because the test is dependent on the distribution of the sample mean differences, which is presumed to be normally distributed, this assumption is required.
The standard error of the mean difference and the construction of confidence intervals both need the assumption of normality. Other techniques, including non-parametric testing, may be more suited if the population distribution is not normal.
To know more about hypothesis, visit,
https://brainly.com/question/606806
#SPJ4
identify the key features of f(x)=√(x+1) -2



Answers
Answer: Represent functions using function notation. MM1A1b: Graph the basic functions f(x) = xⁿ, where n = 1 to 3, f(x) = √x, f(x) = 1*1 and f(x) = 1∕x. ... MM1A1f: Recognize sequences as functions with domains that are whole numbers.
Step-by-step explanation:
What types of concurrent constructions are needed to find the centroid of a triangle?
Answers
The types of concurrent constructions that are needed to find the centroid of a triangle include the following: B. intersection of the lines drawn to the midpoint of each side of the triangle to its opposite vertex.
What is the centroid theorem?In Mathematics and Geometry, the centroid theorem states that the centroid of a triangle is located at two-third (2/3) of the distance from the vertex to the midpoint of the (opposite) sides.
Generally speaking, the centroid of a triangle simply refers to the point where the three (3) medians of the triangle meet or intersect. This ultimately implies that, a centroid is a point of intersection of the lines from each vertex of a triangle to the midpoint of the opposite sides.
In this context, the types of concurrent constructions would be modeled by answer option B.
Read more on centroid theorem here: brainly.com/question/20627009
#SPJ1
Complete Question:
What types of concurrent constructions are needed to find the centroid of a triangle.
A. intersection of the lines drawn from each vertex of a triangle and perpendicular to its opposite side.
B. intersection of the lines drawn to the midpoint of each side of the triangle to its opposite vertex.
C. intersection of the lines drawn to bisect each vertex of the triangle.
D. intersection of the lines drawn perpendicular to each side of the triangle through its midpoint
15) Find x, y and z. **** Choose 3 Answers
x =52
X= 25
y = 25
y = 65
Z = 25
z = 90

Answers
Answer:
x= 52
y= 25
z= 90
pls mark me as BRAINLIAST
Put these fraction in order of size smallest to largest : 7/10, 2/3, 4/5, 11/15
Answers
7/10=0.7
2/3=0.667
4/5=0.8
11/15=0.733
Answer:
2/3, 7/10, 11/15 and 4/5
Step-by-step explanation:
2/3=0.66
7/10=0.7
11/15=0.73
4/5=0.8
a successful proof can turn a conditional statement into a theorem.T/F
Answers
The given statement "A successful proof can indeed turn a conditional statement into a theorem.'' is true because a successful proof can transform a conditional statement into a theorem by providing a logical and rigorous demonstration of its truth based on the given hypothesis.
In mathematics, a conditional statement is a proposition that asserts a relationship between two or more mathematical objects or concepts. It consists of a hypothesis and a conclusion.
A conditional statement is typically expressed in the form "If A, then B," where A represents the hypothesis and B represents the conclusion.
To establish a conditional statement as a theorem, one needs to provide a valid proof that demonstrates the truth of the statement. A proof is a logical argument that follows a series of logical deductions from axioms, definitions, and previously established theorems.
When a proof is successfully constructed for a conditional statement, it provides rigorous justification for the truth of the conclusion based on the given hypothesis.
By demonstrating the logical validity and coherence of the argument, the proof confirms the truth of the conditional statement and establishes it as a theorem.
The process of proving a conditional statement involves carefully reasoning through logical steps, utilizing mathematical principles and logical inference rules.
It requires precise and accurate reasoning, ensuring that each step in the proof is valid and consistent with the underlying mathematical framework.
Once a conditional statement has been proven, it is elevated to the status of a theorem. Theorems are fundamental results in mathematics that have been rigorously proven and hold true within a given mathematical system.
They serve as building blocks for further mathematical investigations and form the foundation of mathematical knowledge.
In summary, a successful proof can transform a conditional statement into a theorem by providing a logical and rigorous demonstration of its truth based on the given hypothesis.
To know more about conditional statement refer here:
https://brainly.com/question/14457027#
#SPJ11
The power for a one-sided test of the null hypothesis = 10 versus the alternative = 8 is equal to 0.8. Assume the sample size is 25 and = 4. What is , the probability of a Type I error?
Answers
The probability of a Type I error is 0.2 or 20%. This means that there is a 20% chance of rejecting the null hypothesis when it is actually true.
The power of a hypothesis test is the probability of rejecting the null hypothesis when the alternative hypothesis is true. In this case, the power of the test is given as 0.8, and the null hypothesis is that the true value of the parameter is 10, while the alternative hypothesis is that the true value is 8.
We are given the sample size, n = 25, and the standard deviation, σ = 4. To calculate the probability of a Type I error, we need to determine the significance level of the test, denoted by α.
The significance level is the probability of rejecting the null hypothesis when it is actually true. It is usually set before conducting the test, and commonly set at 0.05 or 0.01.
To calculate α, we can use the following formula:
α = 1 - power = 1 - 0.8 = 0.2
So, the probability of a Type I error is 0.2 or 20%. This means that there is a 20% chance of rejecting the null hypothesis when it is actually true.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
In the Diagram segment ad bisects angle bac

Answers
Since segment AD bisects angle BAC, the value of x is equal to 14.6.
What is an angle bisector?In Mathematics, an angle bisector can be defined as a type of line, ray, or segment, that bisects or divides a line segment exactly into two (2) equal angles.
By applying the angle bisector theorem to this triangle (ΔABC), we have:
AB/BD = AC/DC
19/x = 17/(20 - x)
17x = 19(20 - x)
17x = 380 - 19x
19x + 17x = 380
26x = 380
x = 380/26
x = 14.6.
In conclusion, we can reasonably infer and logically deduce that the value of x in triangle ABC is 14.6.
Read more on angle bisector here: brainly.com/question/18714022
#SPJ1