Which statement is true regarding the functions on the
graph?
° f(2) = g(2)
° f(0) = g(0)
° f(2)= g(0)
° f(0) = g(2)

Answers
Answer:
f(2) = g(2)
General Formulas and Concepts:
Alg I
Reading a Cartesian PlaneIdentifying CoordinatesSolutions of systems of equationsStep-by-step explanation:
We see from the graph that f(x) and g(x) intersect at x = 2. Therefore, the point at x = 2 would be equivalent in both graphs/be a solution to both equations.
Therefore, f(2) must equal g(2), as they intersect each other at that point and have the same value of 0.
Answer: A f(2) = g(2)
Step-by-step explanation: look at the picture

Related Questions
Can someone please provide a step-by-step explanation for the answer?
If the universe of discourse is the real numbers, give the truth value of each of the
following propositions:
(a) ∀x∃y(x = y²)
(b) ∀x∃y(x² = y)
(c) ∃x∀y(xy = 0)
(d) ∀x∃y(x + y = 1)

Answers
The Propositions are resulting
(a) ∀x∃y(x = y²) is False
(b) ∀x∃y(x² = y) is True.
(c) ∃x∀y(xy = 0) is True.
(d) ∀x∃y(x + y = 1) is True.
(a) ∀x∃y(x = y²)
This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².
Therefore, the proposition (a) is false.
(b) ∀x∃y(x² = y)
For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.
Therefore, the proposition (b) is true.
(c) ∃x∀y(xy = 0)
The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.
Therefore, the proposition (c) is true.
(d) ∀x∃y(x + y = 1)
To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.
Therefore, the proposition (d) is true.
Learn more about Proposition here:
https://brainly.com/question/30695879
#SPJ1
Random sample of 250 students taken with a population of 7500 surveyed about their majors. In the sample, 75 students were Art majors. How many students in total population are are Art majors?
Answers
Therefore, we estimate that there are 2250 Art majors in the total population.
What is proportion?In mathematics, a proportion is an equation that states that two ratios are equal. A ratio is a comparison of two quantities expressed as a fraction or a decimal. Since both sides of the equation are equal, the proportion is true. Proportions are used in many mathematical and real-world contexts, such as in geometry, finance, and statistics. They are useful for comparing and scaling quantities, and for solving problems involving unknown quantities or variables.
Here,
We can use proportions to estimate the total number of Art majors in the population based on the proportion of Art majors in the sample.
The proportion of Art majors in the sample is:
75/250 = 0.3
We can assume that this proportion is representative of the proportion of Art majors in the population.
So, if x is the total number of Art majors in the population, then we can set up the following proportion:
0.3 = x/7500
To solve for x, we can cross-multiply and simplify:
0.3 * 7500 = x
x = 2250
To know more about proportion,
https://brainly.com/question/31010676
#SPJ1
Pls help Darnell is an election officer. On election day, he travels to the polling place, which is 4.4 miles away from his home. On a map of Harrison County, these two places are 8 inches apart. What is the scale of the map? Write your answer in simplest form using whole numbers.
Answers
Answer:
The scale of the map is 1 : 34848---------------------------------
Real distance is 4.4 miles and on the map it is 8 inches.
The scale is:
8 in : 4.4 miles = Divide both sides by 81 in : 0.55 milesor
1 in : 0.55 * 63360 in = Convert 1 mile = 63360 inches1 : 34848Help please ASAP thanks

Answers
Answer: 71º
Step-by-step explanation:
I cant remeber the therum but basically its just the opposite, super simple!!
What is the simplified value of the expression below?
StartFraction 7 times 8 + 20 (4.5) over 16 times 0.5 EndFraction
18.25
21.38
110.25
119.50
Answers
Answer:
C: 110.25
Step-by-step explanation:
The simplification form of the provided expression is 18.25 option (A) is correct.
What is an expression?It is defined as the combination of constants and variables with mathematical operators.
We have a mathematical expression:
\(= \rm \dfrac{7\times8+20(4.5)}{16\times0.5}\)
= (56 + 90)/8
= 146/8
= 18.25
Thus, the simplification form of the provided expression is 18.25 option (A) is correct.
Learn more about the expression here:
brainly.com/question/14083225
#SPJ2
George is putting trim around his rectangular deck, including the gate. He will need 40 feet of trim to do the entire deck. if the deck is 12 feet long, how wide is the deck
Answers
The width of the deck given that the entire deck needs 40 feet to trim is 8 feet
How to determine how wide the deck isLet's assume the width of the rectangular deck is "w".
The perimeter of the deck can be calculated by using the formula: P = 2(l + w), where P is the perimeter, l is the length, and w is the width.
Here, the length of the deck is given as 12 feet.
So, P = 2(12 + w)
We also know that the total trim required is 40 feet.
So, P = 40 feet
Equating both the expressions for P, we get:
2(12 + w) = 40
Simplifying the equation, we get:
24 + 2w = 40
2w = 16
w = 8
Therefore, the width of the deck is 8 feet.
Read more about perimeter at
https://brainly.com/question/25092270
#SPJ1
Daniel bought 3 sweaters that each cost the same amount and a jacket that cost $40. The items he bought cost a total of $100 before tax was added. What was the cost of each sweater? Write an equation that represents this situation and solve.
Please somebody help with this question, thanks!!!.
Answers
subtract 40 from both sides
3x= 60
divide by 3
x=20
each Sweater cost 20
Pls I need help ASAP rn

Answers
Answer:
C (40)
Step-by-step explanation:
8^2 + 15^2 = C^2
64 + 225 = C^2
289 = C^2
17 = C
It's asking for the permiter, so you have to add up all the sides:
8 + 15 + 17 = 40
Calculate the maturity value of simple interest a seven months loan of $6,000 if the interest rate is 7.6%
Answers
ANSWER
\(6266\)EXPLANATION
Given;
\(\begin{gathered} p=6000 \\ R=7.6\% \\ T=\frac{7}{12} \end{gathered}\)Now using the formula for simple interest
\(I=\frac{PRT}{100}\)substituting the values we have;
\(\begin{gathered} I=\frac{6000\times7.6\times7}{100\times12} \\ =266 \end{gathered}\)Now the interest after 7 months would be
\(266\)The maturity value is
\(\begin{gathered} P+I \\ =6000+266 \\ =6266 \end{gathered}\)(a) Use appropriate algebra and Theorem to find the given inverse Laplace transform. (Write your answer as a function of t.)
L−1 {3s − 10/ s2 + 25}
(b) Use the Laplace transform to solve the given initial-value problem.
y' + 3y = e6t, y(0) = 2
Answers
(a) Expand the given expression as
\(\dfrac{3s-10}{s^2+25}=3\cdot\dfrac s{s^2+25}-2\cdot\dfrac5{s^2+25}\)
You should recognize the Laplace transform of sine and cosine:
\(L[\cos(at)]=\dfrac s{s^2+a^2}\)
\(L[\sin(at)]=\dfrac a{s^2+a^2}\)
So we have
\(L^{-1}\left[\dfrac{3s-10}{s^2+25}\right]=3\cos(5t)-2\sin(5t)\)
(b) Take the Laplace transform of both sides:
\(y'(t)+3y(t)=e^{6t}\implies (sY(s)-y(0))+3Y(s)=\dfrac1{s-6}\)
Solve for \(Y(s)\):
\((s+3)Y(s)-2=\dfrac1{s-6}\implies Y(s)=\dfrac{2s-11}{(s-6)(s+3)}\)
Decompose the right side into partial fractions:
\(\dfrac{2s-11}{(s-6)(s+3)}=\dfrac{\theta_1}{s-6}+\dfrac{\theta_2}{s+3}\)
\(2s-11=\theta_1(s+3)+\theta_2(s-6)\)
\(2s-11=(\theta_1+\theta_2)s+(3\theta_1-6\theta_2)\)
\(\begin{cases}\theta_1+\theta_2=2\\3\theta_1-6\theta_2=-11\end{cases}\implies\theta_1=\dfrac19,\theta_2=\dfrac{17}9\)
So we have
\(Y(s)=\dfrac19\cdot\dfrac1{s-6}+\dfrac{17}9\cdot\dfrac1{s+3}\)
and taking the inverse transforms of both sides gives
\(y(t)=\dfrac19e^{6t}+\dfrac{17}9e^{-3t}\)
(02.02 MC)
If trapezoid ABCD was reflected over the y-axis, reflected over the x-axis, and rotated 180°, where would point A′′′ lie?
Trapezoid formed by ordered pairs A at negative 4, 1, B at negative 3, 2, C at negative 1, 2, D at 0, 1.
(1, −1)
(−4, 1)
(1, 1)
(−4, −1)
Answers
The location of point A''' after the three transformations would be (-4, 1).
To determine the location of point A''', we need to apply the three transformations (reflection over the y-axis, reflection over the x-axis, and rotation of 180°) to point A.
When a point is reflected over the y-axis, the x-coordinate is negated while the y-coordinate remains the same.
So, the reflection of point A (-4, 1) over the y-axis would be (4, 1).
When a point is reflected over the x-axis, the y-coordinate is negated while the x-coordinate remains the same. So, the reflection of point (4, 1) over the x-axis would be (4, -1).
When a point is rotated 180°, the x-coordinate and y-coordinate are both negated. So, the rotation of point (4, -1) by 180° would be (-4, 1).
To learn more on Transformation click:
https://brainly.com/question/11709244
#SPJ1
What is the value of p?133990°OA. 133°B. 90°C. 43°O D. 47°

Answers
ANSWER:
The value of x is 43°
STEP-BY-STEP EXPLANATION:
We know that the sum of the internal angles in a triangle is equal to 180°
We also know that the sum of the internal and external angle is also equal to 180°
Therefore:
The first thing is to calculate the value of the internal angles, like this
\(\begin{gathered} 180-133=47 \\ 180-90=90 \end{gathered}\)replacing:
\(\begin{gathered} 180=47+90+p \\ p=180-47-90 \\ p=43 \end{gathered}\)What is the value of x in the figure shown below?
5.5
3.4 82°
A
5.5
38°
B
20
3.4
D

Answers
Check the picture below.

Matthew examines the relation shown in the below.
{(4,-11), (3,1), (0,1), (2,6), (3, -1)}
Is the relation a function? Why or why not?
No. There are x values which map to more than 1 y-value.
Yes. Every y-value maps to exactly 1 x-value.
No. There are y-values which map to more than 1 x-value.
Yes. Every x-value maps to exactly 1 y-value.
Answers
No, there are x values which map to more than 1 y-value.
Given that Matthew examines the relation as shown in the below.
{(4, -11), (3,1), (0,1), (2,6), (3, -1)}
We need to check whether the relation is a function or not,
So, we know that,
A relation can map inputs to multiple outputs. It is a function when it maps each input to exactly one output. The set of all functions is a subset of the set of all relations.
If any x values are repeated, and the corresponding y values are different, then we have a relation and not a function.
Here we can see that the y values are repeated, so it is not a function.
Learn more about functions click;
https://brainly.com/question/31062578
#SPJ1
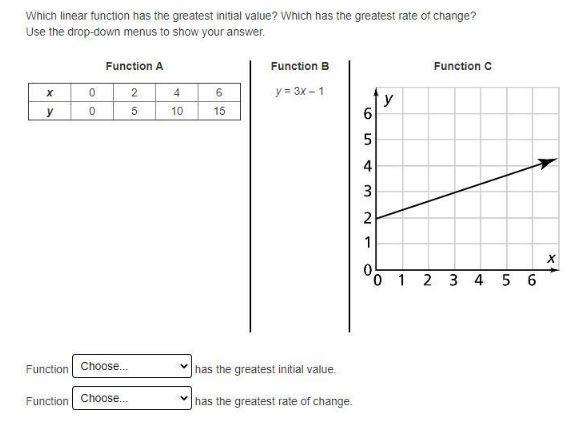
Which linear function has the greatest initial value? Which has the greatest rate of change?
Use the drop-down menus to show your answer.
WILL GIVE BRANLIEST IF ANSWERED

Answers
The linear function C has the greatest initial value is 2. And the linear function B that has the greatest rate of change is 3.
The complete question is attached below.
What is the equation of line?The equation of line is given as
y = mx + c
Where m is the slope and c is the y-intercept.
Then the equations of the functions A, B, and C is given as
Function A: y = 5/2 x
Function B: y = 3x - 1
Function C: y = 1/3x + 2
Then graph of the functions is given below.
The linear function C has the greatest initial value is 2.
The linear function B that has the greatest rate of change is 3.
More about the equation of line link is given below.
https://brainly.com/question/21511618
#SPJ1

what is 38 as a product of prime
Answers
Answer:
38 = 1 x 38 or 2 x 19. Factors of 38: 1, 2, 19, 38. Prime factorization: 38 = 2 x 19
Simply expression
Please show steps

Answers
Answer:
3(x + 5y) - 2(x + y)
3x + 15y - 2x - 2y
x + 13y
(3x + 15y) + (-2x + -2y)
x + 13y
Please help me with my homework!
Alexis says she is thinking about a number whose absolute value is 19. What are the possible numbers she could be thinking of? Mark them on the number line.

Answers
Answer:
-19 and 19
Step-by-step explanation:
The only values that have an absolute value of 19 are -19 and 19.
The Price of Pollo
In El Salvador, "Country Chicken" is the most popular fried chicken franchise
in the country. Like most fast-food establishments, they provide a carry-out
service on their menu. You can buy their chicken in several different
quantities: 2, 6, 9, 15, or 21 pieces per box.
Over the years, prices have steadily risen, as things have a way of doing in
many areas of modern life. For example, on July 1, 1993, a box of two
pieces cost 8.35 colones, and on December 31, 1995, that same purchase
would cost you 11.25 colones.
(Note: prices are given in their original Salvadorean currency, colones; $1 U.S
colones.)
Using these two data 'points', you can form a linear equation of the slope-inter
mx + b. The independent variable x is time; the dependent variable y represe
Your task for this problem is to:
1. Find this equation.
2. Use your equation to predict what the price should have been for a 2
July 1, 1999.
Answers
Answer:
Hope I helped!~
Step-by-step explanation:
To find the equation of the line, we can use the slope-intercept form of the equation:
y = mx + b
where m is the slope of the line and b is the y-intercept.
Using the two data points given, we can calculate the slope:
m = (11.25 - 8.35) / (1995 - 1993) = 1.95
To find the y-intercept, we can use one of the data points:
8.35 = 1.95(1993) + b
b = -3884.65
So the equation of the line is:
y = 1.95x - 3884.65
To predict the price of a box of two pieces on July 1, 1999, we can substitute x = 6 (since 1999 is 6 years after 1993) into the equation:
y = 1.95(6) - 3884.65
y = 11.7 - 3884.65
y = -3872.95
This gives us a negative price, which obviously does not make sense. It is likely that the price of a box of two pieces was not linearly increasing during this time period, or that there were other factors influencing the price. Therefore, we cannot use this equation to accurately predict the price of a box of two pieces on July 1, 1999.
Piecewise linear relations

Answers
The required piecewise linear relations are f(x) = 4 if [0, 2), and f(x) = -2x + 8 if [2, 4).
What is a piecewise function?A piecewise-defined function (also known as a piecewise function or a hybrid function) is a function defined by multiple sub-functions, each of which applies to a different interval of the main function's domain (a sub-domain).
The graph is given in the question, as shown
f(x) = 2x + 4 if [-2, 0]
This the sub-function define between the interval [-2, 0].
f(x) = 4 if [0, 2)
This the sub-function define between the interval [0, 2).
f(x) = -2x + 8 if [2, 4)
This the sub-function define between the interval [2, 4).
Learn more about the piecewise function here:
https://brainly.com/question/12700952
#SPJ1
The sum of the squared differences of scores from their mean is zero.
True or False?
Answers
Answer:
False
Step-by-step explanation:
We have several terms that we can take reference to in this true or false situation. The first is Central Tendency which measures for locating a single score that's most representative or descriptive of all scores in a distribution.
Given text:
The sum of the squared differences of scores from their mean is zero.
The main term within this sentence is the word mean. This term is the sum of a set divided by the total (#) of scores summed.
In order to determine whether this is true or false, we must list what is referred to as the 5 characteristics of the term Mean.
1. Changing an existing score will change the mean.
2.Adding a new score or removing an existing score will change the mean, unless that value equals the mean.
3. Adding, subtracting, multiplying, or dividing each score in a distribution by a constant will cause the mean to change by that constant.
4. The sum of the differences of scores from their mean is zero.
5. The sum of the squared differences of scores from their mean is minimal.
After taking closer analysis, there has been clarification within the characteristics of the mean confirming that the answer is indeed false.
#SPJ1
Diseases tend to spread according to the exponential growth model. In the early days of AIDS, the growth multiplier (i.e. common ratio) was around 2.0. In 1983, about 1800 people in the U.S. died of AIDS. We can use the exponential model:
P
n
=
1800
(
2.0
n
)
.
If the trend had continued unchecked, how many people would have died from AIDS in 2004?
Answers
If the trend had continued unchecked, 3,774,873,600 people would have died from AIDS in 2004
How many people would have died from AIDS in 2004?The equation of the function is given as
P(n) = 1800(2.0)^n
Where n represents the number of years since 1983
There are 21 years from 1983 to 2004
This is calculated as
n = 2004 - 1983
n = 21
Substitute 21 for n in the equation P(n) = 1800(2.0)^n
So, we have
P(21) = 1800(2.0)^21
Evaluate
P(21) = 3774873600
Hence, if the trend had continued unchecked, 3,774,873,600 people would have died from AIDS in 2004
Read more about exponential model at:
https://brainly.com/question/27161222
#SPJ1
HELPPPPPP PLEASE I AM STRUGLING]
![HELPPPPPP PLEASE I AM STRUGLING]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qit2mdTQcYii48p4GpHsBTaPT7M8sEiP.png)
Answers
10 is the answer
why are you struggling
so simple
hope it helps you ❣❣Mark me as brainliest
Hi, image is shown below. Please help if able to.. thank you.

Answers
Answer:
50 days
Step-by-step explanation:
Grace=3x+200
Joseph=6x+50
3x+200=6x+50
3x=150
x=50
Evaluate the function at each specified value of the independent variable and simplify. (If an answer is undefined, enter UNDEFINED.) g(y) = 3 − 2y
(a) g(0) =
(b) g(3over2)=
(c) g(s + 1) =
Answers
Answer:
UNDEFINED
Step-by-step explanation:
Can't further simplify the function
Write as a ratio in lowest terms. 2 feet to 36 inches
Answers
Answer: 1:18
Step-by-step explanation:
Answer:
2 inches : 3 inches
Step-by-step explanation:
Start with turning the 2 feet into inches
2(12)
24
Then to simplify a ratio just find the Greatest Common Factor, which is 12 in this case
24:36
\(\frac{24}{12} : \frac{36}{12}\)
= 2:3
Check for extraneous solutions when plugging -7 into x-5=2(x+1).
Check for extraneous solutions when plugging 1 into x-5=-2(x+1)
Please hurry
Answers
There are no extraneous solutions when plugging -7 into x-5=2(x+1).
So extraneous solutions means the solutions that you get by solving an equation, but after you try plugging it back into your original equation, the solution does not work.
Now we have our solutions of x=7, and we just need to check whether it is extraneous or not. We can do this by taking x=1 and plugging it back into your original equation x - 5 = 2(x + 1)
x - 5 = 2(x + 1)
-7 - 5 = 2(-7 + 1)
-12 = -14 + 2
-14 + 14
0 = 0
We end up getting that 0 = 0 which is correct,
Thus, there are no extraneous solutions.when plugging -7 into x-5=2(x+1).
To learn more about extraneous solutions refer here
https://brainly.com/question/12361474
#SPJ9
What is the solution to this equation?
7x-3(x-6)= 30
A. X= 3.
B. x = 12
C. X= 9
D. x=6
Answers
Answer:
A
Step-by-step explanation:
To solve the equation 7x-3(x-6)=30, we need to use the distributive property to simplify the left-hand side of the equation:
7x - 3(x-6) = 30
7x - 3x + 18 = 30
4x + 18 = 30
Next, we need to isolate the variable term on one side of the equation. To do this, we can subtract 18 from both sides:
4x + 18 - 18 = 30 - 18
4x = 12
Finally, we can solve for x by dividing both sides by 4:
4x/4 = 12/4
x = 3
Therefore, the solution to the equation 7x-3(x-6)=30 is x = 3. Answer A is correct.
Solve 4|x + 5| + 8 = 24.
A. x= 1 and x = -1
B. x = -1 and x = 9
C. x = 1 and 2 = -9
D. x= -1 and x = -9
Answers
consider the following code segment, which is intended to store the sum of all multiples of 10 between 10 and 100, inclusive (10 20 ... 100), in the variable total. int x
Answers
The missing code that can be used to replace / missing code / so that the code segment works as intended is x >= 10.
The code segment is intended to store the sum of all multiples of 10 between 10 and 100, inclusive. The value of x starts at 100 and is decremented by 10 on each iteration of the loop, until it reaches 10. The sum of all the multiples of 10 between 10 and 100 is stored in the variable total.
The missing code in the while statement determines when the loop will stop. If we use x >= 10 as a replacement for / missing code /, the loop will run as long as x is greater than or equal to 10. When x reaches 10, the loop will stop.
Here's the complete code:
int x = 100;
int total = 0;
while(x >= 10)
{
total = total + x;
x = x - 10;
}
Learn more about looping and control structures here: https://brainly.com/question/14515869
#SPJ4
Your question is incomplete but probably the complete question is:
Consider the following code segment, which is intended to store the sum of all multiples of 10 between 10 and 100, inclusive (10 + 20 + ... + 100), in the variable total.
int x = 100;
int total = 0;
while( / missing code / )
{
total = total + x;
x = x - 10;
}
Which of the following can be used as a replacement for / missing code / so that the code segment works as intended?
A x < 100
B x <= 100
C x > 10
D x >= 10
E x != 10