which two line are parallel? how do you know A.2x-y=5 B.2x+y=3 C.y=2x+3
Answers
To know if two lines are parallel when defined in the xy-plane is to compare the slopes.
If the slopes are equal, the lines are parallel.
In order to compare the slopes, we need to put them in the form:
\(y=mx+b\)Then, we have for A:
\(\begin{gathered} 2x-y=5 \\ y=2x-5 \end{gathered}\)B.
\(\begin{gathered} 2x+y=3 \\ y=-2x+3 \end{gathered}\)C.
\(y=2x+3\)The only lies that have the same slope, hence, they are parallel, are A and C (slope: 2).
Note: B is perpendicular to A and C as the slope of B is the slope of A but opposite sign (multiplied by -1).
Related Questions
the standard deviation of f$ ar{x},f$ is usually called the
Answers
The standard deviation of f$ ar{x},f$ is usually called the "sample standard deviation".
This is a commonly used statistical measure that represents the amount of variation or dispersion within a set of data. It is calculated by taking the square root of the variance, which is the average of the squared differences from the mean.
The sample standard deviation is often used to compare the variability of different sets of data and to determine the significance of differences between them. Financial contracts known as derivatives are those entered into by two or more parties and whose value is derived from an underlying asset,
collection of assets, or benchmark. A derivative may be traded over-the-counter or on an exchange. Derivative prices are based on changes in the underlying asset.
To know more about derivative click here
brainly.com/question/29096174
#SPJ11
Please help me with this one!!

Answers
Answer:
\(21 in^{2}\)
Step-by-step explanation:
The square in the middle has a length and width of 3, so multiply. 9.
All of the triangles have a base of 3 and a height of 2. The area equation for triangles is
\(A=bh\frac{1}{2}\)
So base*height is 6. Divide that by 2 or multiply by 1/2.
You get 3. There are 4 triangles, so multiply that by 4. 12.
Add 12 and 9 together, and you get:
\(21 in^{2}\)
I hope this helps!
How many different two digit numbers can be formed from the digits, 7,8, and 9 if the numbers must be even and no digit can be repeated?
Answers
Answer:
2
Step-by-step explanation:
If the number must be even, the units digit must be 8. That leaves 2 choices for the tens digit. The possible numbers are ...
78
98
There are 2 of them.
Answer: Only two: 78 and 98
Step-by-step explanation: 8 is the only even number available to put in the units place where even or odd is determined. With no repetition allowed, the only possibilities left are to switch positions of the 7 and 9 in the tens place.
Solve the following system of equations:(1 point) x − 2y = 6 2x − 4y = 10
Answers
The value of the variables on the equation:
x - 2y = 6 and 2x - 4y = 10 is 0.
What is the variables in the equation?An equation is the statement that illustrates the variables given. In this case, two or more components are taken into consideration to describe the scenario.
The equation is illustrated thus:
x - 2y = 6 ..... i
2x - 4y = 10 ... . ii
Equation ii can be reduced to x - 2y = 5
The equation will be:
x - 2y = 6
x - 2y = 5
Subtract the equations
In this case, the equations will give 0. It can't be solved further than this.
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
A binary (categorical) predictor should not be used along with nonbinary (numerical) predictors O True False
Answers
Binary predictors behave like any other except they look weird on a scatter plot.
False, a binary (categorical) predictor should not be used along with nonbinary (numerical) predictors
What is a binary operator?It is important to note that binary and non-binary predictors can both be utilized.
Categorical variables with two possible outcomes, such as yes/no or true/false, are represented by binary predictors. On the other hand, nonbinary predictors indicate numerical variables that can have a variety of values.
It is feasible to capture the links between several sorts of variables and enhance the predictive ability of a model by using both types of predictors. Utilizing methods like logistic regression and
Learn more about binary operator at: https://brainly.com/question/32042263
#SPJ4
the following data represent the means for each treatment condition in a two-factor experiment. note that one mean is not given. what value for the missing mean would result in no main effect for factor a?
Answers
The value for the missing mean which would result in no main effect for Factor as calculated from the given data , A is 2
Given ,
B1 B2
A1 6 8
B1 12 ?
Let X = missing mean
mean of A1,
( 6 + 8 ) / 2 = 14 / 2 = 7
mean of A2
(12 + x ) / 2 = 7
x + 12 = 14\x = 14 -12 = 2
Therefore the value for the missing mean would result in no main effect for Factor A is 2
In addition to the mode and median, the mean is one of the measurements of central tendency. Simply put, the mean is the average of the values in the given set. It indicates that values in a particular data set are distributed equally. The three most frequently employed measures of central tendency are the mean, median, and mode.
The total values provided in a datasheet must be added, and the sum must be divided by the total number of values in order to determine the mean.
To learn more about missing mean
https://brainly.com/question/19569311
#SPJ4
What is the right translation of these expressions and equations? (with solution)
1. 7 - 2m
2. 3( m + 2) = 15
3. 5m - m(2 - m)
Answers
Answer:
7 - 2m can be translated to "7 minus two times m" or "the difference between 7 and twice m".
3(m + 2) = 15 can be translated to "three times the sum of m and 2 is equal to 15" or "the product of 3 and the sum of m and 2 is 15".
To solve the equation, we can start by distributing the 3 on the left side:
3(m + 2) = 15
3m + 6 = 15
Then, we can subtract 6 from both sides:
3m + 6 - 6 = 15 - 6
3m = 9
Finally, we can divide both sides by 3:
3m/3 = 9/3
m = 3
Therefore, the solution to the equation 3(m + 2) = 15 is m = 3.
5m - m(2 - m) can be translated to "5m minus the product of m and the difference between 2 and m" or "the difference between 5m and m times the quantity 2 minus m".
To simplify the expression, we can use the distributive property to expand the second term:
5m - m(2 - m) = 5m - 2m + m^2 = m^2 + 3m
Therefore, the simplified expression is m^2 + 3m.
What is 20% of 14.98
Answers
Answer:
2.996
Step-by-step explanation:
14.98 * 0.20 = 2.996
Hope this helps!
I NEED AN ANSWER FAST
2. If x = -8, which inequality is true?
A. -3x - 2 = 24
B. 12 + 2x > 9
C. 4x -19 318
D. 17 + x>10
Answers
The equation would add up to 9, and 9 is less than 10
Answer:
[C] 4x - 19 < 318
Step-by-step explanation:
For [C] I think you meant: [C] 4x - 19 < 318
Since, x = -8
then we can plug it in to each answer choice to find the answer:
[A] -3x - 2 = 24
⇒ -3(-8) - 2 = 24
-3(-8) = 24
24 -2 = 22 not 24
False.
[B] 12 + 2x > 9
⇒ 12 + 2(-8) > 9
12 -16 > 9
-4 > 9
False.
[C] 4x -19 < 318
⇒ 4(-8) -19= 318
-51 < 318
True.
[D] 17 + x>10
⇒ 17 + (-8) >10
-25 > 10
False.
Hence, the answer is [C] 4x - 19 < 318
Kavinsky
determine whether the series is convergent or divergent. [infinity] 8 en 3 n(n 1) n = 1
Answers
The series ∑[n=1 to ∞] \(8e^n\) / (3n(n+1)) is convergent.
How we determine the series?To determine whether the series ∑[n=1 to ∞] \(8e^n\) / (3n(n+1)) is convergent or divergent, we can apply the ratio test.
Using the ratio test, we calculate the limit as n approaches infinity of the absolute value of the ratio of the (n+1)-th term to the n-th term:
lim(n→∞) |\((8e^(^n^+^1^) / (3(n+1)(n+2))) / (8e^n / (3n(n+1)))\)|
Simplifying the expression:
lim(n→∞) |\((8e^(^n^+^1^) * 3n(n+1)) / (8e^n * 3(n+1)(n+2))\)|
The common factors cancel out:
lim(n→∞) |e * n / (n+2)|
As n approaches infinity, the ratio tends to e, which is a finite non-zero value.
Since the ratio is a constant (e), which is less than 1, the series is convergent by the ratio test.
Learn more about Convergent
brainly.com/question/28202684
#SPJ11
someone this is due at 11:59 i will give brainliest
A student misses 6 questions on an exam. His final score was an 80%\
how many questions were on the test

Answers
EASY GEOMETRY! SOMEONE PLS HELP!
Part A: An angle is two collinear rays with a common endpoint. Find an example that contradicts this definition. How would you change the definition to make it more accurate? (5 points)
Part B: Give an example of an undefined term and how it pertains to angles. (5 points)
Answers
To make the definition more accurate, we should change it to: "An angle is formed by two non-collinear rays with a common endpoint."
Part A:
The given definition of an angle is incorrect, as it states that an angle is two collinear rays with a common endpoint. In reality, an angle is formed by two non-collinear rays with a common endpoint. An example that contradicts the given definition would be two rays that are collinear, which means they lie on the same line. In this case, no angle would be formed.
Part B:
An example of an undefined term in geometry is a "point." A point is a basic building block of geometric concepts and does not have a specific definition but is used to define other terms. It pertains to angles because angles are formed by two rays with a common endpoint, which is a point. The concept of a point helps us understand and visualize the formation of angles.
to learn more about common endpoint click here:
brainly.com/question/10727163
#SPJ11
(SOMEONE HELP ASAPP )In triangle QRS below, 2Q = 53.13º and ZR = 36.87°
Which of the following are true?

Answers
Can you please show the triangle?
What's the prime factorization of 663
Answers
A prime number is a number which has exactly two factors its self and on not prime.
The orange divisor above are the prime factors of the number 663 if we put all of it together we have the factors 3*13*17=663. it can also be written in exponential form as 3^1 * 13^1 * 17^1.
Answer:
3 x 13 x 17
Step-by-step explanation:
a gorcery store sells a smal case of 6 bottles of water $4 and large case of q8 bottles for $10. Is the price per bottle pf water proportional?
Answers
6 bottles for $4 each bottle cost $1.50
one more than the difference between 18 and 7 times a number is -9
eight times a number plus 6 less than twice the number is 34
twelve less than the quotient of a number and 8 is -1
i don't think they're supposed to be fractions as going over the others in class didn't and tried checking over my work
Answers
Answer:
The difference between 18 and seven times a number: 18 - 7x
Step-by-step explanation:
(ii) One more than the difference between 18 and seven times a number:
Add 1 to the expression from step (i) and get
1 + (18 - 7x)
(iii) One more than the difference between 18 and seven times a number is -9:
Set expression from step (ii) equal to -9 and get
1 + (18 - 7x) = -9
You can simplify and solve for x.
3. What is the volume of the prism shown?
5.27 in
8.13 in
9.69 in
6.81 in

Answers
The volume of the prism shown is equal to 145.89 cubic inches.
How to calculate the volume of a triangular prism?In Mathematics and Geometry, the volume of a triangular prism can be determined or calculated by using the following formula:
Volume of triangular prism, V = 1/2 × b × h.
Where:
b represent the base area of a triangular prism.h represent the height of a triangular prism.By substituting the given dimensions (side lengths) into the formula for the volume of a triangular prism, we have;
Volume of triangular prism, V = 1/2 × 5.27 × 8.13 × 6.81
Volume of triangular prism, V = 291.775131/2
Volume of triangular prism, V = 145.89 cubic inches.
Read more on triangular prism here: brainly.com/question/21173224
#SPJ1
The volume of the prism is 145.89 cubic inches.
To find the volume of a prism, multiply the area of the base by the height of the prism.
We know the formula for the volume of a triangular prism is:
\(V = \frac{1}{2}\times b \times h\)
Where:
b represent the base area of a triangular prism.
h represent the height of a triangular prism.
Therefore, we can calculate the volume of the prism by cubing the length of one of its sides:
\(V = \frac{1}{2}\times 5.27\times 8.13 \times 6.81\)
\(V= \frac{291.775131}{2}\)
\(V = 145.89\) cubic inches.
For such more question on volume
https://brainly.com/question/28795033
#SPJ8
A stone is thrown horizantally with a velocity of 50 m/s from the top of a building. Find its velocity after 2 seconds.
Answers
Answer:
V = 53.7 m/s ∠-21.41°
Step-by-step explanation:
Since the stone's initial vertical velocity, u is 0m/s(since it is thrown horizontally), we find the stone's final vertical velocity, v from v = u - gt where u and v have the meanings as given above, g = acceleration due to gravity = 9.8 m/s² and t = time = 2 s
So, v = u - gt
v = 0 m/s - 9.8 m/s² × 2 s
v = 0 m/s - 19.6 m/s
v = - 19.6 m/s
Since the stone's horizontal velocity is u' = 50 m/s, we find the resultant magnitude of velocity V from V = √(u'² + v²)
So, V = √((50 m/s)² + (-19.6 m/s)²)
V = √(2500 m²/s² + 384.16 m²/s²)
V = √(2884.16 m²/s²)
V = 53.7 m/s
Its direction Ф = tan⁻¹(v/u')
Ф = tan⁻¹(-19.6 m/s/50 m/s)
Ф = tan⁻¹(-0.392)
Ф = -21.41°
So it velocity V = 53.7 m/s ∠ -21.41°
suppose a juice box contains 30% juice with the remaining portion of the drink composed of water. what is the solute in this type of juice box?
Answers
Suppose a juice box contains 30% juice with the remaining portion of the drink composed of water alcohol is the solute in this type of juice box.
Ethanol; Ethanol, a drab liquid with a pleasing scent this is produced evidently from fermentation through yeasts and different microorganisms. It is utilized in alcoholic beverages, as a solvent, and withinside the manufacture of different chemicals. Ethanol is a fairly poisonous and colorless compound.
Alcohol is the solute in this type of juice box is the solvent as alcohol is easily soluble as the solvent and has best property of a solute and csn pass through the semipermeable permeability and others solvent also. The alcohol is actually acting as the solute here to dissolve the solvent.
Read more about the solute;
https://brainly.com/question/16083884
#SPJ4
You are standing above the point (2,4) on the surface z=15−(3x
2
+2y
2
). (a) In which direction should you walk to descend fastest? (Give your answer as a unit 2-vector.) direction = (b) If you start to move in this direction, what is the slope of your path? slope = The temperature at any point in the plane is given by T(x,y)=
x
2
+y
2
+3
100
. (c) Find the direction of the greatest increase in temperature at the point (−2,2). What is the value of this maximum rate of change, that is, the maximum value of the directional derivative at (−2,2)? (d) Find the direction of the greatest decrease in temperature at the point (−2,2). What is the value of this most negative rate of change, that is, the minimum value of the directional derivative at (−2,2)?
Answers
a) The direction in which you should walk to descend fastest is: (-12, -16)
b) The slope of your path is: -88
c) The direction of the greatest increase in temperature at the point (−2, 2) is: (-4, 4)
The maximum rate of change is: 4√2
d) The direction of the greatest decrease is: (4, -4).
The most negative rate of change is: 4√2
How to solve Directional Derivative Problems?(a) The equation on the surface is:
z = 15 - (3x² + 2y²)
The gradient of this surface will be the partial derivatives of the equation. Thus:
Gradient of the surface z:
∇z = (-6x, -4y)
Since you are standing above the point (2,4), then the direction to descend fastest is:
∇z(2,4) = (-6(2), -4(4))
∇z(2,4) = (-12, -16)
That gives us the direction to descend fastest is in the direction.
(b) If you start to move in the direction (-12, -16) above, then slope of your path (rate of descent) is given by the dot product expressed as:
Slope = ∇z(2,4) · (-12, -16)
= (2)(-12) + (4)(-16)
= -24 - 64
= -88
(c) We want to find the direction of the greatest increase in temperature at the point (−2,2).
Thus, the gradient of T(x,y) is given by:
∇T = (2x, 2y).
The direction is:
∇T(-2, 2) = (2(-2), 2(2))
∇T(-2,2) = (-4, 4)
The maximum rate of change is:
∇T(-2,2) = √((-4)² + 4²)
= √(16 + 16)
= √(32)
= 4√2
(d) The direction of the greatest decrease is:
(-∇T(-2, 2)) = (-(-4), -4)
= (4, -4).
The most negative rate of change is:
∇T(-2, 2) = √(4² + (-4)²)
= √(16 + 16)
= √(32)
= 4√2
Read more about Directional Derivatives at: https://brainly.com/question/30048535
#SPJ4
An arch is in the shape of a parabola. It has a span of 364 feet and a maximum height of 26 feet.
Find the equation of the parabola.
Determine the distance from the center at which the height is 16 feet.
Answers
The equation of the parabola is given as follows:
y = -16/33124(x - 182)² + 26.
The distance from the center at which the height is 16 feet is given as follows:
38.12 ft and 325.88 ft.
How to obtain the equation of the parabola?The equation of a parabola of vertex (h,k) is given by the equation presented as follows:
y = a(x - h)² + k.
In which a is the leading coefficient.
It has a span of 364 feet, hence the x-coordinate of the vertex is given as follows:
x = 364/2
x = 182.
It has a maximum height of 26 feet, hence the y-coordinate of the vertex is obtained as follows:
y = 26.
Considering that h = 182 and k = 26, the equation is:
y = a(x - 182)² + 26.
When x = 0, y = 0, hence the leading coefficient a is obtained as follows:
33124a + 26 = 0
a = -26/33124
Hence:
y = -16/33124(x - 182)² + 26.
For a height of 16 feet, we have that
y = 16
16/33124(x - 182)² = 10
(x - 182)² = 33124 x 10/16
(x - 182)² = 20702.5.
Hence the heights are:
x - 182 = -sqrt(20702.5) -> x = -sqrt(20702.5) + 182 = 38.12 ft.x - 182 = sqrt(20702.5) -> x = sqrt(20702.5) + 182 = 325.88 ft.More can be learned about quadratic functions at https://brainly.com/question/1214333
#SPJ1
The__________of an angle is the point where the sides of the angle intersect
Help please<3
Answers
Help me please, I’ll give brainliest!!

Answers
Answer:
A line that is perpendicular to y=2/5x-5 must have a slope of -5/2, but a line parallel to line y=5/2x+6 must have a slope of 5/2, and these slopes do not match up.
Explanation:
In order for a line to be parallel to another line, they must have the same slope. In order for a line to be perpendicular to another line, their slopes must be opposite reciprocals (meaning that when they are multiplied, the product is -1). From here you can find what slope the line must have to perpendicular or parallel to another line, and then you can see that the answers to not match up to be the same line!
Hope this helped :)
suppose you have three possible risk scenarios x, y, and z. your initial assessment found that x is twice as likely as z, and y is three times as likely as z. what is p(x), p(y), and p(z)?
Answers
Given,Three possible risk scenarios X, Y and Z. The initial assessment found that X is twice as likely as Z and Y is three times as likely as Z.
Probability of X is p(X) = 2p(Z)
Probability of Y is p(Y) = 3p(Z)
Probability of Z is p(Z)Let the probability of Z be p. So, the probability of X and Y can be written as:
p(X) = 2p(Z)p(Y) = 3p(Z). And, Total probability, p(X) + p(Y) + p(Z) = 1. Given that, p(X) + p(Y) + p(Z) = 12p(Z) + 3p(Z) + p(Z) = 1(6p(Z) = 1)p(Z) = 1/6. Therefore, p(X) = 2p(Z) = 2(1/6) = 1/3p(Y) = 3p(Z) = 3(1/6) = 1/2. Hence, the probability of X, Y, and Z are p(X) = 1/3, p(Y) = 1/2, and p(Z) = 1/6 respectively.
To know more about Probability refer here:
https://brainly.com/question/30034780
#SPJ11
The expression in each circle is the result of the sum of the two non outlined boxes connected to it, complete writing the expression in simplified form.
4x+3y---------(5x+7y)---------x+4y
! !
! !
! !
(Blank.) (4x+5y)
! !
! !
2x-y---------(Blank)-----------3x+y
Answers
Answer:
5x
Step-by-step explanation:
Answer/Step-by-step explanation:
The circle by your left:
(4x + 3y) + (2x - y)
Distribute +1
4x + 3y + 2x - y
Add like terms together
6x + 2y
The rectangle by at the bottom right:
(4x + 5y) - (x + 4y)
Distribute -1
4x + 5y - x - 4y
Group like terms
4x - x + 5y - 4y
3x + y
The circle at the bottom middle:
(2x - y) + (3x + y)
Distribute +1
2x - y + 3x + y
Group like terms
2x + 3x - y + y
5x
A test started at 10:55. the teacher collected the answer scripts 1 hour and 15 minutes later . At what time did she collect them?
Answers
Answer:
10+1=11 but the 55 so it is now 11:55+15min so it makes it 12:10
Answer:
Hello! The answer to your question is 12:10.
Step-by-step explanation:
1 hour after 10:55 is equivalent to 11:55. Now, we have 15 minutes remaining. We can add in increments of 5 to get to 15 in terms of time:
11:55 + 5 minutes
= 12:00 + 5 minutes
= 12:05 + 5 minutes
= 12:10
5 + 5 + 5 = 15, so we reached 15.
The teacher collected the answer scripts at 12:10.
Is this proportional? What is the function tule? How do you know?

Answers
A function rule describes how to convert an input value (x) into an output value (y) for a given function.
it’s not constant throughout the table. or doesn’t have the same rate through the table.
nine packeges of basil cost $27 how many packeges of basil can you buy with $9
Answers
Answer:
3 packages of basil
Step-by-step explanation:
27/9 = 3 --> each package costs $3
9/3 = 3 --> amount of packages you can buy with $9
The diagram shows a triangle.
All the measurements are in cm.
The perimeter of the triangle is 70 cm.
The area of the triangle is A cm.
Work out the value of A.
4x + 1
3x - 1
-
Зх
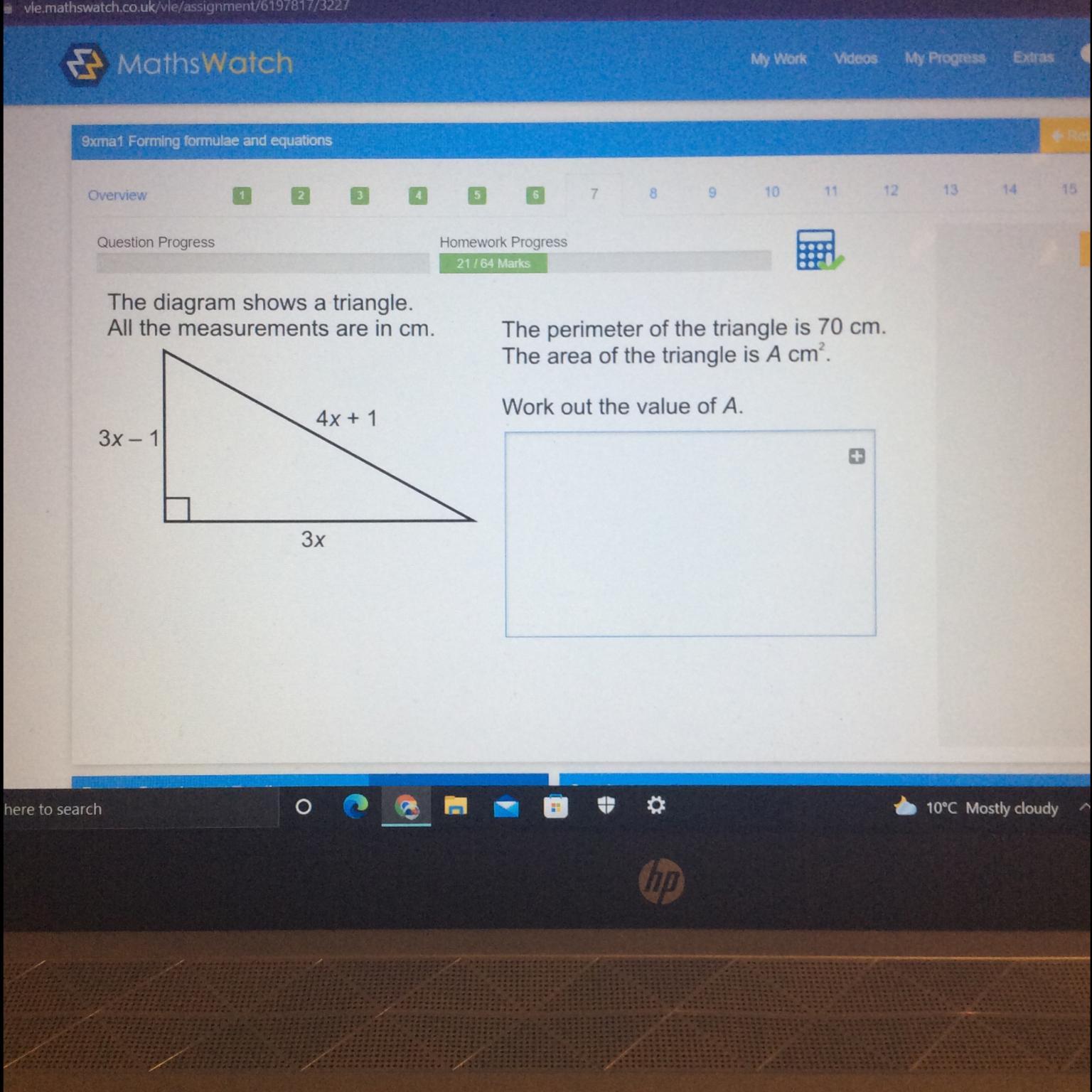
Answers
Answer: 210
Explanation:
Recall that the perimeter is the distance around the figure. It's the amount of fencing needed to enclose such a shape.
Add up all three sides and set the sum equal to the perimeter 70. Then solve for x.
side1+side2+side3 = perimeter
(3x)+(3x-1)+(4x+1) = 70
10x = 70
x = 70/10
x = 7
We can then calculate each side
horizontal leg = 3x = 3*7 = 21vertical leg = 3x-1 = 3*7-1 = 21-1 = 20hypotenuse = 4x+1 = 4*7+1 = 28+1 = 29Notice how 21+20+29 = 70 to confirm we have the correct side lengths.
Once we know the horizontal and vertical leg (aka base and height), we can find the area.
Area = 0.5*base*height
Area = 0.5*21*20
Area = 210 square cm
Step-by-step explanation:
first you have to find x . Then you can add them and equal them with triangle area.


what is the simple interest on 5000 for 219 days 4% per annum
Answers
The simple interest on 5000 for 219 days at 4% per annum would be $120.
What is the formula for simple interest?The formula for simple interest is -
A = P(1 + rt)
Given is a to find simple interest on $5000 for 219 days at 4% per annum.
We can write the interest as -
I = P x R x T
I = 5000 x 0.04 x 0.6
I = 120
Therefore, the simple interest on 5000 for 219 days at 4% per annum would be $120.
To solve more questions on simple interest, visit the link -
brainly.com/question/30098550
#SPJ1