While filing your income tax, you report annual contributions of $100 to a public radio station, $300 to PBS (television station), $150 to a woman’s shelter, and $450 to other charitable organizations.
Find your monthly expense.
Answers
Hey there! I'm happy to help!
Let's add up all of these contributions.
100+300+150+450=1000
However, this is annual. We want monthly. So, we simply divide by 12.
1000/12≈83.33
Therefore, the monthly expense is $83.33
I hope that this helps! Have a wonderful day!
Related Questions
URGENT *EASY 10 POINTS* : Show steps to get the expression ln(sqrt(2) +1) - ln(1/sqrt(2)) equal to -ln(1-(1/sqrt2))
Answers
Answer:
Step-by-step explanation:
To show that the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\), we can simplify both sides of the equation using the properties of logarithms. Here are the steps:
Step 1: Simplify the expression on the left side:
\(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\)
Step 2: Apply the logarithmic property \(\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)\) to combine the logarithms:
\(\ln\left(\frac{\sqrt{2} + 1}{\frac{1}{\sqrt{2}}}\right)\)
Step 3: Simplify the expression within the logarithm:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)}\right)\)
Step 4: Simplify the denominator by multiplying by the reciprocal:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)} \cdot \sqrt{2}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right) \cdot \sqrt{2}}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
Step 5: Simplify the numerator:
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
\(\ln\left(\sqrt{2}(\sqrt{2} + 1)\right)\)
\(\ln\left(2 + \sqrt{2}\right)\)
Now, let's simplify the right side of the equation:
Step 1: Simplify the expression on the right side:
\(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\)
Step 2: Simplify the expression within the logarithm:
\(-\ln\left(\frac{\sqrt{2} - 1}{\sqrt{2}}\right)\)
Step 3: Apply the logarithmic property \(\ln\left(\frac{a}{b}\right) = -\ln\left(\frac{b}{a}\right)\) to switch the numerator and denominator:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
Step 4: Simplify the expression:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
\(-\ln\left(\frac{\sqrt{2}(\sqrt{2} + 1)}{1}\right)\)
\(-\ln\left(2 + \sqrt{2}\right)\)
As we can see, the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) simplifies to \(\ln(2 + \sqrt{2})\), which is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\).
Emilio made 51 potholders. Each potholder cost him $2.80 to make. If he sells each potholder for $3.26, how much profit will he make =)
Answers
Answer:
Your answer will be $166.26
Step-by-step explanation:
i found this out because i multiplied 51 times 3.26
For what values of a and b is x^64 + ax^b +25 a perfect square for all integer values of x?
Answers
For the expression \(x^64 + ax^b + 25\) to be a perfect square for all integer values of x, b must be 64, and a must be a perfect square, written as a = \(y^2.\)
To determine the values of a and b such that the expression\(x^64 + ax^b\) + 25 is a perfect square for all integer values of x, we need to analyze the properties of perfect squares.
A perfect square is an expression that can be written as the square of another expression. In this case, we want the given expression to be in the form of\((x^n)^2,\) where n is an even integer.
Let's examine the given expression: \(x^64 + ax^b\) + 25
For it to be a perfect square, the quadratic term \(ax^b\)must have the same exponent as the leading term\(x^6^4.\) This means b must be equal to 64.
So we have:\(x^64 + ax^64 + 25\)
Now, we can rewrite this as:\((x^32)^2 + 2(x^32) (\sqrt{a}) + (\sqrt{25})^2\)
By comparing this with the standard form of a perfect square, (\(x^n +\sqrt{k} )^2\), we can deduce that √a must be equal to x^32 and \(\sqrt{25}\) must be equal to \(\sqrt{k.}\)
Therefore, we have: \(\sqrt{a} = x^3^2\)and\(\sqrt{25} = \sqrt{k}\)
From the second equation, we know that k = 25.
Now, substituting the value of k back into the first equation, we have: \(\sqrt{a} = x^3^2\)
To satisfy this equation for all integer values of x, a must be a perfect square. Therefore, we can express a as a =\(y^2\), where y is an integer.
For more such information on: expression
https://brainly.com/question/1859113
#SPJ8
Put =, >, or < between
-0.171100011 _____ -0.171100010
Answers
Answer:
Put "<" between -0.171100011 _____ -0.171100010
Step-by-step explanation:
-0.171100010 is greater than -0.171100011 because they are negative numbers so -0.171100011 is further than -0.171100010 to 0, therefore -0.171100010 is greater.
Mark brainliest if this helped :)
In the 2012 Olympics a U.S. athlete Nathan Adrian finished the 100-meter freestyle swim in 47.52 seconds. If nathan swam the same pace in a regular 25-meter pool what would his time have been per lap?
Answers
At the same rate as his 100-meter freestyle swim in the 2012 Olympics, Nathan Adrian could have completed one loop of a 25-meter pool in 11.88 seconds.
To solve this problem
The idea of proportionality can be applied. The time it would take Nathan Adrian to complete one lap in a 25-meter pool is known to be 47.52 seconds for the 100-meter freestyle. Since the tempo is constant while the distance varies, we can establish a ratio:
100 meters / 47.52 seconds = 25 meters / x seconds
where x is the unknown time for one lap in the 25-meter pool.
To solve for x, we can cross-multiply:
100 meters * x seconds = 47.52 seconds * 25 meters
100x = 1188
Dividing both sides by 100, we get:
x = 11.88 seconds
Therefore, at the same rate as his 100-meter freestyle swim in the 2012 Olympics, Nathan Adrian could have completed one loop of a 25-meter pool in 11.88 seconds.
Learn more about idea of proportionality here : brainly.com/question/870035
#SPJ1
Determine which ordered pair(s) lies on the function
f(x) = -25^x+1
[] (1, 625)
[] (0, -25)
[] (-1, -1)
Answers
Parallel lines j and k are cut by a transversal l. Which pair of angles are alternate interior angles?
A. 2 and 5
B. 2 and 6
C. 4 and 2
D. 1 and 7

Answers
Answer:
1 and 7
Step-by-step explanation:
Given that,
The parallel lines j and k are cut by a transversal l.
We need to find the pair of angles are alternate interior angles.
Angles that are on opposite sides of the transversal and are in between the other two lines are alternate angles.
In this figure, angles 1 and 7 form alternate interior angles. Hence, the correct option is (D).
Answer:3 and 7
Stepby-step explanation:
please help me figure this out
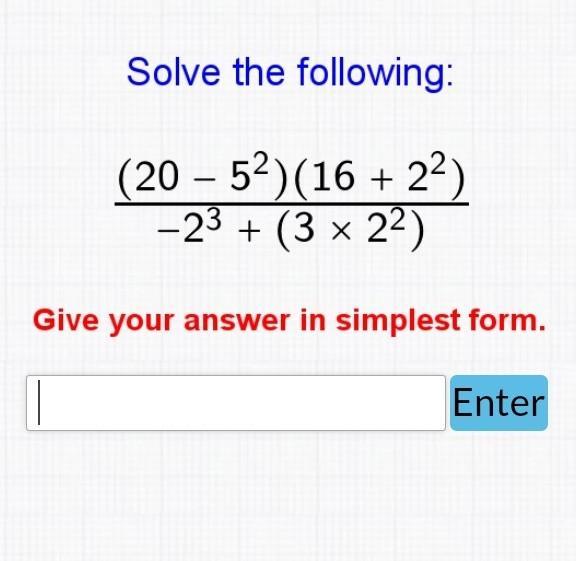
Answers
Answer:
-25
Step-by-step explanation:
\( \dfrac{(20 - 5^2)(16 + 2^2)}{-2^3 + (3 \times 2^2)} = \)
First, do all exponents.
\( = \dfrac{(20 - 25)(16 + 4)}{-8 + (3 \times 4)} \)
Now do each operation in parentheses.
\( = \dfrac{(-5)(20)}{-8 + 12} \)
Multiply in the numerator. Add in the denominator.
\( = \dfrac{-100}{4} \)
Divide the numerator by the denominator.
\( = -25 \)
Answer:
-25
Step-by-step explanation:
PEMDAS
The PEMDAS rule is an acronym representing the order of operations in math:
ParenthesesExponentsMultiplication and Division (from left to right)Addition and Subtraction (from left to right)Given expression:
\(\sf \dfrac{(20-5^2)(16+2^2)}{-2^3+(3 \times 2^2)}\)
As the given expression is a fraction, carry out the operations in the numerator and denominator first before finally dividing them.
Following PEMDAS, carry out the calculations inside the parentheses first, then carry out the rest of the calculations following the order of operations:
Parentheses
Calculate the exponents inside the parentheses:
\(\implies \sf \dfrac{(20-25)(16+4)}{-2^3+(3 \times 4)}\)
Multiply:
\(\implies \sf \dfrac{(20-25)(16+4)}{-2^3+(12)}\)
Add and subtract:
\(\implies \sf \dfrac{(-5)(20)}{-2^3+(12)}\)
Exponents
Calculate the exponent:
\(\implies \sf \dfrac{(-5)(20)}{-8+(12)}\)
Multiply and Divide
Multiply:
\(\implies \sf \dfrac{-100}{-8+(12)}\)
Add and Subtract
Add:
\(\implies \sf \dfrac{-100}{4}\)
Finally, divide the numerator by the denominator:
\(\implies \sf -25\)
Solve 2x²-x-6=0 by factorisation
Answers
Answer:
x = 2, x = -3/2
Step-by-step explanation:
Factors to be (x-2)(2x+3) = 0
x =2, x = -3/2
Answer:
Step-by-step explanation:
2x²-x-6=0
2x²-(4-3)x-6=0
2x²-4x+3x-6=0
2x(x-2)+3(x-2)=0
(x-2)(2x+3)=0
pless i really need help

Answers
Perimeter of the parallelogram = 210 in.
Area of parallelogram = 2,484 in.²
What are the Perimeter and Area of a Parallelogram?Perimeter of parallelogram = 2(a + b), where a and b are its sides.
Area of parallelogram = (b)(h), where h is its height and b is the length of one of its bases.
Given:
a = 51 in.
b = 54 in.
h = 46 in.
Perimeter of the parallelogram = 2(54 + 51) = 210 in.
Area of parallelogram = (b)(h) = (54)(46) = 2,484 in.²
Learn more about parallelogram on:
https://brainly.com/question/3050890
#SPJ1
how to calculate area when you are given volume of 182m3 and height of 2.8m
Answers
Hey there!
We simply have to do 182/2.8, and you will get the area (65m^2).
We know that the formula for area is length x width, and the formula for volume is length x width x height. In the volume formula, we can see it can also be area x height to get volume. So, we know that area x height = volume, right? And in this equation, we are given volume and height. If V = ha, with V = volume; h = height; a = area, we can divide "h" on both sides, and we get V/h = a, or volume divided by height is area. To solve for the above equation, we can plug the numbers in the formula: 182/2.8 = a, or 65 = a.
Hope this helps! Have an amazing day, and remember, you've got this!
The coordinates of the vertices of a polygon are shown on the graph below.
What is the name of the polygon?
octagon
pentagon
quadrilateral
triangle

Answers
Answer:
Triangle
Step-by-step explanation:
It has three side unlike the others can't have three sides
Will give brainlist!!! Please help

Answers
Answer:
total is (12-4=5(^19 <6>) THIS IS MY ANWER
A rancher wishes to build a fence to enclose a rectangular pen having area 24 square yards. Along one side the fence is to be made of heavy duty material costing $6 per yard, while the remaining three sides are to be made of cheaper material costing $3 per yard. Determine the least cost of fencing for the pen.
Answers
At the point of the least cost of fencing the cost function has a zero
derivative.
The least cost of fencing for the pen is $72.00Reasons:
Shape of the pen = Rectangular
Area of the pen = 24 yd²
Cost of material on one side of the fence = $6 per yard
Cost of material on the remaining three sides = $3 per yard
Required:
The least cost of fencing the pen
Solution:
The least cost is a minimum value of the cost function
Let L represent the length of the fence and let W represent the width of the fence
We have;
The perimeter of the fence = 2·L + 2·W
The area of the pen, A = L × W = 24
One of the length, L, of the fence costs $6 per yard and the other length L,
of the opposite side costs $3 per yard.
The cost of fencing, C 3 × 2·W + 3 × L + 6 × L = 6·W + 9·L
C = 6·W + 9·L
\(\displaystyle W = \mathbf{\frac{24}{L}}\)
Which gives;
\(\displaystyle C = 6 \cdot \frac{24}{L} + 9 \cdot L = \frac{144}{L} + 9 \cdot L = \mathbf{\frac{144 + 9 \cdot L^2}{L}}\)
The shape of the above function is concave upwards.
At the minimum value, we have;
\(\displaystyle \frac{dC_{min}}{dL} = \frac{d}{dL} \left(\frac{144}{L} + 9 \cdot L\right) = 9 - \frac{144}{L^2} = 0\)
Which gives;
\(\displaystyle \frac{144}{L^2} = 9\)
\(\displaystyle \frac{144}{9} = L^2\)
By symmetric property, we have;
\(\displaystyle L^2 = \frac{144}{9}\)
\(\displaystyle L = \sqrt{ \frac{144}{9}} = \frac{12}{3} = 4\)
The length of the fence that gives the least cost, L = 4 yards
\(\displaystyle At \ L = 4, \ W = \frac{24}{4} = 6\)
The width of the fence at least cost, W = 6 yards
Cost, C = 6·W + 9·L
Least cost, \(C_{min}\) = 6 × 6 + 9 × 4 = 72
The least cost of the fencing, \(C_{min}\) = $72.00
Learn more about the minimum values of a function here:
https://brainly.com/question/7243840

What color is the height?
Area= 1/2 base . height
I gave Brainlist

Answers
Answer:
The red one?
Step-by-step explanation:
Sorry if my answer is wrong
NO LINKS!! URGENT HELP PLEASE!!!
What formula can you use if the sides are slanted/diagonal to find the lengths?

Answers
Answer:
If you have the coordinates of two points, you can use the distance formula to find the length of the line segment between them. The distance formula is:
\(d =\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
where:
d is the distance between the two pointsx1 and y1 are the coordinates of the first pointx2 and y2 are the coordinates of the second pointAnd to find a perimeter add all the sides as the perimeter is the sum of all sides of the shape or object.
Perimeter: Sum of all sides
Area : Length * breadth or base*height for rectangle
Helpppppp PLEASEEE GIVING BRAINLIEST

Answers
Answer:
-12x + 5 > -19
-12x > -24
x < 2
C 5) Identify 2/10 as a decimal. * O 10.2 2.10 O .2 o O .02
Answers
Answer:
0.2
Step-by-step explanation:
need as soon a posible within 2 minutes enjoy your points

Answers
Answer:
(x+6)^2+(y-7)^2= 29
Step-by-step explanation:
general exqn-> (x-h)^2+(y-k)^2=(r)^2
here, h= -6 and k=7
r= √ 29
Therefore, exqn of circle=
(x+6)^2+(y-7)^2= 29
Answer:
(x + 6)² + (y - 7)² = 29
Step-by-step explanation:
the equation of a circle in standard form is
(x - h )² + (y - k )² = r²
where (h, k ) are the coordinates of the centre and r is the radius
here (h, k ) = (- 6, 7 ) and r = \(\sqrt{29}\) , then
(x - (- 6) )² + (y - 7)² = (\(\sqrt{29}\) )² , that is
(x + 6 )² + (y - 7 )² = 29
Does the graph represent a function? Why or why not ?

Answers
Answer:
A.
Step-by-step explanation:
The vertical line test is a way of finding out if a relation is a function.
Graph the relation.
Then imagine a vertical line moving from left to right over the graph of the relation.
If the vertical line intersects at most one point of the graph in any position you place the vertical line, then the relation is a function.
This function passes the vertical test since it never intersects more than one point on the vertical line at a time.
Answer: A.
help plssssssssssssss

Answers
Answer:
Step-by-step explanation:
Figure 1 = (-1,1)
Figure 2 = (-2,5)
So the answer should be x + (-1) and y + (4)
A truck with 30-in.-diameter wheels is traveling at 50 mi/h.
Find the angular speed of the wheels in rad/min, "hint convert miles to inches & hours to minutes:
_________rad/min
How many revolutions per minute do the wheels make?
___________rpm
Answers
Answer:
A. the angular speed is 3771.4 rad/min
b. 5921 rpms
Step-by-step explanation: I just got this same question right on a test.
Shen the trainer has two solo workout plans that he offers his clients: Plan A and Plan B. Each client does either one or the other (not both). On Wednesday there were clients who did Plan A and who did Plan B. On Thursday there were clients who did Plan A and who did Plan B. Shen trained his Wednesday clients for a total of hours and his Thursday clients for a total of hours. How long does each of the workout plans last?
Answers
The length of time that it will take for each of the workout sessions would be: Plan A = 1.5 hours, and Plan B = 0.5 hours.
What would be the length of the sessions?The length of the sessions can be obtained by first obtaining drawing a system of equations for the two cases. On Wednesday, we can represent the sessions as follows:
2A + 12B = 9 hours
On Thursday, we would have
5A + 3B = 9 hours
2A + 12B = 9 Eqn 1
5A + 3B = 9 Eqn 2
Multiply equation 2 by -4
2A + 12B = 9
-20A - 12B = -36
2A - 20A = 9 -36
-18A = -27
Divide both sides by -18
A = 1.5 hours
For B, substitute A in the first equation
2(1.5) + 12B = 9
3 + 12B = 9
12B = 9 - 3
12B = 6
Divide both sides by 12
B = 0.5
Learn more about simultaneous equations here:
https://brainly.com/question/148035
#SPJ1
Complete Question:
Ann the trainer has two solo workout plans that she offers her clients: Plan A and Plan B. Each client does either one or the other (not both). On Wednesday there were 2 clients who did Plan A and 12 who did Plan B. On Thursday there were 5 clients who did Plan A and 3 who did Plan B. Ann trained her Wednesday clients for a total of 9 hours and her Thursday clients for a total of 9 hours. How long does each of the workout plans last?
Factor this expression.
3х2 - 15х
O A. 3(x - 5)
O B. 3(x2 - 5)
O C. 3x(x2 - 5)
O D. 3x(x - 5)
Answers
Answer:
D
Step-by-step explanation:
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
=
Find the x and y intercepts of the graph of the equation: y= |3x-7|. Select all that
apply.
Answers
0 = |3x - 7|
We can split this into two cases: 3x - 7 = 0 and 3x - 7 = 0. Solving each case, we get:
Case 1: 3x - 7 = 0
3x = 7
x = 7/3
Case 2: -(3x - 7) = 0 (Note that we use the negative sign outside the absolute value to account for the other case)
3x - 7 = 0
3x = 7
x = 7/3
So the x-intercept is (7/3, 0).
To find the y-intercept, we need to set x = 0 and solve for y:
y = |3(0) - 7|
y = |-7|
y = 7
So the y-intercept is (0, 7).
Therefore, the answer is:
- The x-intercept is (7/3, 0).
- The y-intercept is (0, 7).
Aanya lives in Ohio. She immigrated with her family from India to North America. Aanya wants to visit a cousin in Toronto by driving. The gate person at the Peace Bridge in Buffalo, NY tells her that Toronto is 500 km north on Highways 400/401. How far is that in miles? After Aanya arrives, she and her cousin compare efficiencies of their cars. Aanya’s car averages 30 mi/gallon, but she needs to convert that to km/liter. Using the conversions 1 km = 0.62 mi, 1 mi = 1.61 km, and 1 qt = 0.946 liters, determine the distance from the Peace Bridge to Toronto in miles and the efficiency of Aanya’s car in km/liter (hint on the latter—first get km/gallon, then km/liter). Both parts of an answer must be correct.
(a) 300 mi, 48.3 km/liter (b) 310 mi, 12.76km/liter (c) 320 miles, 14 km/liter
(d) 330 miles, 7.5 km/liter (e) 620 miles, 48.3 km/liter (f) none of the above
Answers
Answer:
(b) 310 mi, 12.76km/liter
Step-by-step explanation:
We are told that Toronto is 500 km north on Highways. Since 1 km = 0.62 mi, then Toronto is: 500 × 0.62 = 310 miles
Aanya’s car averages 30 mi/gallon.
We are told that 1 mi = 1.61 km
Thus, her average is now;
30 × 1.61 km/gallon = 48.3 km/gallon
We are told that 1 qt = 0.946 liters
But also, 0.25 gallon = 1 qt
Thus;
0.25 gallon = 0.946 litres
Thus, 1 gallon = 0.946/0.25 litres = 3.784 litres
Thus, 48.3 km/gallon to km/litres = 48.3/3.784 = 12.76 km/litres
Answer is 310 miles and 12.76 km/litres
what is the scale factor of the dilation
Answers:
A: 3
B:1/4
C:4
D:1/3

Answers
What is the median of the following set of data ?
56.2 112.8 90.4 95.5 103.7 87.6 99.1 112.4 59.7
Answers
Answer: 95.5
Step-by-step explanation:
If you order the numbers from least to greatest and alternate revoking numbers the number in the middle, or median will be 95.5
Bridge Ais 4780 feet long. Bridge B, in the same state, is 650 feet shorter than Bridge A. Find the length of Bridge B.
The length of Bridge Bis feet
Answers
Answer:
4,130
Step-by-step explanation:
4780-650=4130 ft