Who is the dictator of USSR
Answers
Answer:
No. Leaders Date of death
1 Vladimir Lenin January 21, 1924
2 Joseph Stalin March 5, 1953
3 Georgy Malenkov January 14, 1988
4 Nikita Khrushchev September 11, 1971
Step-by-step explanation:
Related Questions
Beth wants to paint the four walls of her rectangular bedroom. Her room is 10 feet wide, 13 feet long, and 8 feet high. She will not paint her
rectangular door, which is 3 feet wide and 7 feet high.
What is the total area of the walls that Beth needs to paint?
Answers
Answer:The answer is 1040
Answer:
Okay so Basically I looked at all the answers people are given and I narrowed it down. Its either 1040 or 1019
Step-by-step explanation:
a red die and a blue die are tossed. what is the probability that the red die shows a three and the blue die shows a number greater than three?
Answers
The probability that the red die shows a three and the blue die shows a number greater than three is 1/12
How to determine the probability of a three and and a number greater than three?From the question, we have the following parameters that can be used in our computation:
Red die
Blue die
The sample space of a die is
{1, 2, 3, 4, 5, 6}
using the above as a guide, we have the following:
P(3) = 1/6
P(Greater than 3) = 1/2
So, we have
P = 1/2 * 1/6
Evaluate
P = 1/12
Hence, the probability of a three and and a number greater than three is 1/12
Read more abot probability at
https://brainly.com/question/31649379
#SPJ1
if p > 5 is prime and p is divided by 10, show that the remainder is 1, 3, 7, or 9
Answers
If p > 5 is prime and p is divided by 10, then the remainders are 1, 3, 7, or 9
The given information, we know that p is a prime number greater than 5, and that p is divided by 10. This means that p must end in either 0 or 5. since those are the only digits that allow for a number to be divisible by 10.
However, we also know that p is prime, which means it cannot be divisible by any number other than 1 and itself. This rules out the possibility of p ending in 0. since any number ending in 0 is divisible by 10 (and therefore not prime).
Therefore, p must end in 5. This means that p can be written in the form:
p = 10n + 5
where n is some integer. Now, let's consider what happens when we divide p by 10:
p/10 = (10n + 5)/10 = n + 0.5
Since p/10 is not an integer (it has a decimal component of 0.5), we know that p cannot be evenly divided by 10. Therefore, when p is divided by 10, there must be a remainder.
To determine what possible remainders there could be, we can look at the possible values for the last digit of p. Since p ends in 5, the last digit can only be 1, 3, 7, or 9 (since these are the only digits that, when multiplied by 5 and added to 10n, result in a number ending in 5).
Therefore, if p > 5 is prime and p is divided by 10, the remainder must be either 1, 3, 7, or 9.
Know more about Prime numbers here :
https://brainly.com/question/145452
#SPJ11
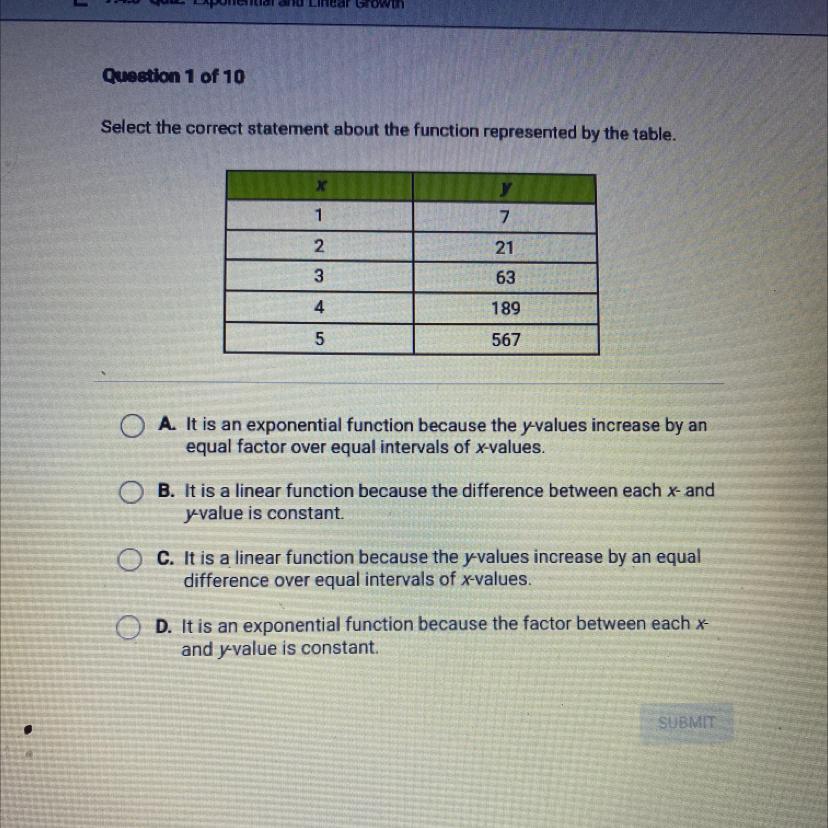
Select the correct statement about the function represented by the table.
X Y
1. 7
2. 21
3. 63
4. 189
5. 567
PLEASEEE HELPPPP
Answers
The correct statement about the function represented by the table is:
It is an exponential function because the factor between each x and y value is constant.
Option D is the correct answer.
What is a function?A function has an input and an output.
A function can be one-to-one or onto one.
It simply indicated the relationships between the input and the output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
In this case, we can see that the ratio between each x and y value is constant.
Specifically, the ratio is 7 between x = 1 and x = 2, 3 between x = 2 and
x = 3, 3 between x = 3 and x = 4, and 3 between x = 4 and x = 5.
Therefore,
The function is exponential.
Additionally, we can observe that the function has the form y = ab^x, where a is the initial value and b is the common ratio.
To find the values of a and b, we can use the first two data points.
y = a x b^x
7 = a x b^1
21 = a x b^2
Dividing the second equation by the first equation.
21 / 7 = (a x b²) / (a x b^1)
3 = b
Substituting b = 3 into the first equation.
7 = a x 3^1
a = 7 / 3
So,
The function represented by the table is:
y = (7/3) x 3^x
which is an exponential function with an initial value of a = 7/3 and a common ratio of b = 3.
Thus,
It is an exponential function because the factor between each x and y value is constant.
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ7
Find the slope of the tangent line to the given polar curve at the point specified by the value of \( \theta \). \[ r=\cos (\theta / 3), \quad \theta=\pi \]
Answers
The derivative of \(r\) with respect to \(\theta\) can be found using the chain rule. Let's proceed with the differentiation:
\frac{dr}{d\theta} = \frac{d}{d\theta}\left(\cos\left(\frac{\theta}{3}\right)\right)
To differentiate \(\cos\left(\frac{\theta}{3}\right)\), we treat \(\frac{\theta}{3}\) as the inner function and differentiate it using the chain rule. The derivative of \(\cos(u)\) with respect to \(u\) is \(-\sin(u)\), and the derivative of \(\frac{\theta}{3}\) with respect to \(\theta\) is \(\frac{1}{3}\). Applying the chain rule, we have:
\frac{dr}{d\theta} = -\sin\left(\frac{\theta}{3}\right) \cdot \frac{1}{3}
Now, let's evaluate this derivative at \(\theta = \pi\):
\frac{dr}{d\theta} \bigg|_{\theta=\pi} = -\sin\left(\frac{\pi}{3}\right) \cdot \frac{1}{3}
The value of \(\sin\left(\frac{\pi}{3}\right)\) is \(\frac{\sqrt{3}}{2}\), so substituting this value, we have:
\frac{dr}{d\theta} \bigg|_{\theta=\pi} = -\frac{\sqrt{3}}{2} \cdot \frac{1}{3} = -\frac{\sqrt{3}}{6}
Therefore, the slope of the tangent line to the polar curve \(r = \cos(\theta / 3)\) at the point specified by \(\theta = \pi\) is \(-\frac{\sqrt{3}}{6}.
Learn more about Tangent Line here :
https://brainly.com/question/31179315
#SPJ11
Find the interval of convergence for the power series ∑n=2[infinity] n(x−5)^n/(5^2n) interval of convergence =
Answers
The interval of convergence for the power series is -20 < x < 30. The interval of convergence is (-infinity, infinity).
To find the interval of convergence for the power series ∑n=2[infinity] n(x−5)^n/(5^2n), we can use the ratio test:
|[(n+1)(x-5)^(n+1)/(5^2(n+1))]/[n(x-5)^n/(5^2n)]| = |(n+1)(x-5)/(25)|
Taking the limit as n approaches infinity, we get:
lim |(n+1)(x-5)/(25)| = |x-5| lim (n+1)/25
Since lim (n+1)/25 = infinity, the series diverges if |x-5| > 25, and the series converges if |x-5| < 25. We need to test the endpoints of the interval to determine if they converge:
When x = 5 - 25 = -20, we have:
∑n=2[infinity] n(-20-5)^n/(5^2n) = ∑n=2[infinity] (-1)^n n(25/400)^n
Using the ratio test, we have:
lim |[(n+1)(25/400)^n+1]/[n(25/400)^n]| = lim |(n+1)/25| = 0
Therefore, the series converges when x = -20.
When x = 5 + 25 = 30, we have:
∑n=2[infinity] n(30-5)^n/(5^2n) = ∑n=2[infinity] n(25/625)^nUsing the ratio test, we have:
lim |[(n+1)(25/625)^n+1]/[n(25/625)^n]| = lim |(n+1)/25| = infinity
Therefore, the series diverges when x = 30.
Therefore, the interval of convergence for the power series is -20 < x < 30.
Learn more about interval of convergence here
https://brainly.com/question/31398445
#SPJ11
Lorelei and Chance run a bakery. They have been making wedding cakes for several years and they have found the time L it takes Lorelei to frost a randomly selected 3-layer cake is approximately Normally distributed with a mean of 37 minutes and a standard deviation of 12 minutes. The time C it takes Chance to decorate a randomly selected 3-layer cake is approximately Normally distributed with a mean of 52 minutes and a standard deviation of 7 minutes. Assume that L and C are independent random variables.
Use the z-table to answer the question.
Let the random variable T = L + C be the total time it takes Lorelei, then Chance to each totally finish a different randomly selected 3-layer wedding cake.
The shape of T is
.
The center of T is Mu Subscript T =
.
The variability of T is Sigma Subscript T =
.
The probability that Lorelei and Chance totally finish a randomly selected 3-layer wedding cake in under 90 minutes is
Answers
Where the above conditions exist,
The shape of T is also Normally distributedMu_T = 89Var(T) = 193Sigma_T = 13.89the probability that Lorelei and Chance totally finish a randomly selected 3-layer wedding cake in under 90 minutes is 0.5287. What is the rationale for the above response?The random variable T = L + C represents the total time it takes Lorelei and Chance to finish a randomly selected 3-layer wedding cake. Since L and C are independent and Normally distributed, T is also Normally distributed with mean:
Mu_T = Mu_L + Mu_C = 37 + 52 = 89
and variance:
Var(T) = Var(L) + Var(C) = 12^2 + 7^2 = 193
So the standard deviation of T is:
Sigma_T = sqrt(Var(T)) = sqrt(193) = 13.89
The shape of T is also Normally distributed, since it is a sum of two independent Normally distributed variables.
To find the probability that Lorelei and Chance finish a randomly selected 3-layer wedding cake in under 90 minutes, we need to calculate the z-score for this value and then find the corresponding probability from the z-table. The z-score is:
z = (90 - 89) / 13.89
= 0.072
From the z-table, we find that the probability of a Z-score less than or equal to 0.072 is 0.5287.
Therefore, the probability that Lorelei and Chance totally finish a randomly selected 3-layer wedding cake in under 90 minutes is 0.5287 or approximately 53%.
Learn more about probability at:
https://brainly.com/question/30034780
#SPJ1
if AB= 2x + 3 and BC= x + 7, find CD explain it too pls
Answers
2x+3=x+7
x=4
So AB = 2(4)+3=11
CD is congruent (similar) to AB, so CD =11
the answer should be 11
Explain why 51 is not a prime number
Answers
Step-by-step explanation:
51 is not a prime number because it is divisible by 1,3 and 17
and we know prime number are only those number who arenot divisible by any other number except 1
Answer:
57 is divisible by 1,3,19 and 57
Step-by-step explanation:
A prime number is a number that is divisible only by 1 and itself; and 57 is not among the numbers like 2,3,5,7,11 etc
Please help me with this, quickly.

Answers
Answer: That would odd.
Are the triangles similar? Explain why or why not

Answers
Answer:
Two triangles are similar if they have:
Step-by-step explanation:
all their angles equal
corresponding sides are in the same ratio
But we don't need to know all three sides and all three angles ...two or three out of the six is usually enough.
There are three ways to find if two triangles are similar: AA, SAS and SSS:
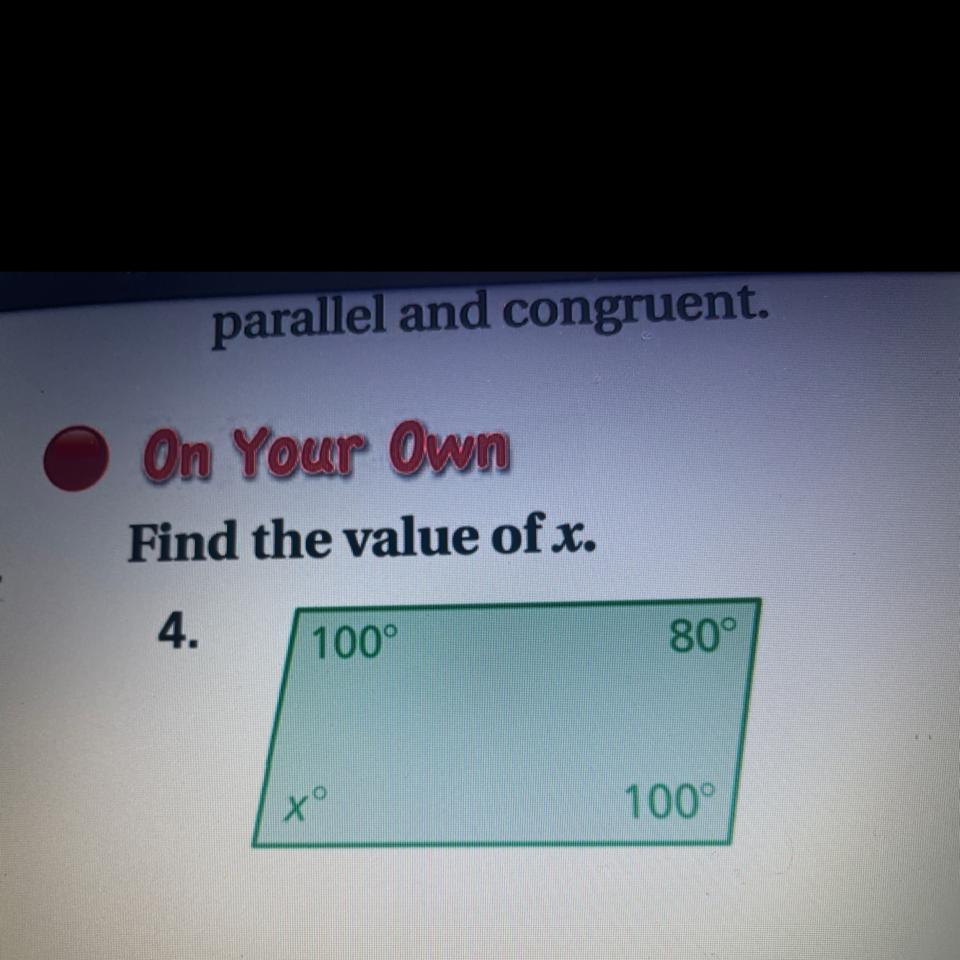
Find the Value of X.
Answers
Answer: 80
Step-by-step explanation:
If you look at the top left and bottom right corner, you see that they are identical, so basically you would do the same to 80.
Well lets see...
Solution 1. The sum of angles of a quadrilateral is 360˚ 100˚+100˚+80˚=280 degrees 360˚-280˚=80˚.
Solution 2. Opposite angles on a parallelogram are equal so x=80˚.
HOPE THIS HELPED!!!!!!!!!!
Please help with this question, thank you.

Answers
Hope this helps, and merry Christmas!!
A sandbox
is
advertised to
hold 240 cubic feet
of sand. If the base
of the sandbox has
an area of 12 square
feet, then what is the
height of the
sandbox?
Answers
Answer:
20
Step-by-step explanation:
240 divided by 12 = 20
PLEASE HELP! 50 Points!
A plane is heading due south with an airspeed of 239 mph. A wind from a direction of 53° is blowing at
10 mph. Find the bearing of the plane.
Answers
The bearing of the plane is approximately 178.037°. \(\blacksquare\)
Procedure - Determination of the bearing of the planeLet suppose that bearing angles are in the following standard position, whose vector formula is:
\(\vec r = r\cdot (\sin \theta, \cos \theta)\) (1)
Where:
\(r\) - Magnitude of the vector, in miles per hour.\(\theta\) - Direction of the vector, in degrees.That is, the line of reference is the \(+y\) semiaxis.
The resulting vector (\(\vec v\)), in miles per hour, is the sum of airspeed of the airplane (\(\vec v_{A}\)), in miles per hour, and the speed of the wind (\(\vec v_{W}\)), in miles per hour, that is:
\(\vec v = \vec v_{A} + \vec v_{W}\) (2)
If we know that \(v_{A} = 239\,\frac{mi}{h}\), \(\theta_{A} = 180^{\circ}\), \(v_{W} = 10\,\frac{m}{s}\) and \(\theta_{W} = 53^{\circ}\), then the resulting vector is:
\(\vec v = 239 \cdot (\sin 180^{\circ}, \cos 180^{\circ}) + 10\cdot (\sin 53^{\circ}, \cos 53^{\circ})\)
\(\vec v = (7.986, -232.981) \,\left[\frac{mi}{h} \right]\)
Now we determine the bearing of the plane (\(\theta\)), in degrees, by the following trigonometric expression:
\(\theta = \tan^{-1}\left(\frac{v_{x}}{v_{y}} \right)\) (3)
\(\theta = \tan^{-1}\left(-\frac{7.986}{232.981} \right)\)
\(\theta \approx 178.037^{\circ}\)
The bearing of the plane is approximately 178.037°. \(\blacksquare\)
To learn more on bearing, we kindly invite to check this verified question: https://brainly.com/question/10649078
15% discount off of $35.
Original:
Discount:
New price
Plz help
Answers
Answer:
It $29.75
Step-by-step explanation:
Answer:
Orignal Price: $35
Discount Price: $29.75
Step-by-step explanation:
The original price is $35 since it says 15% off of $35. To get the discount price you would use the equation 35-15%, which would give you $29.75. Your new price is $29.75.
Hope this is what you were looking for. :D
Can someone please put these in order from least to greatest? Thanks
12x+6y=18
-0.5
12x+1.75
4
Answers
Answer:
Luna wanna play among us with me (sorry I’m bored) the code is: PXQMKF
Step-by-step explanation:
A house has increased in value by 35% since it was purchased. If the current value is 648,000, what was the value when it was purchased?
Answers
Answer:
Purchase rate of the house is $480000.
Step-by-step explanation:
Let the purchase rate of the house = $p
Current value of the house = $648000
If the current rate of the house has increased by 35% of the purchase rate,
Current rate = Purchase rate + 35% of the purchase rate
648000 = p + (35% of p)
648000 = p + \(p\times \frac{35}{100}\)
648000 = p + 0.35p
648000 = (1.35)p
p = \(\frac{648000}{1.35}\)
p = $480000
Therefore, purchase rate of the house is $480000.
Solve the equation. Then check your solution.
6= -2(10n + 7)
A. 1
B 0.4
C. -1
D. 0.05
Answers
Carlos has \dfrac45 5 4 start fraction, 4, divided by, 5, end fraction of a tank of fuel in his car. He uses \dfrac{1}{10} 10 1 start fraction, 1, divided by, 10, end fraction of a tank per day. How many days will his fuel last? Carlos has \dfrac45 5 4 start fraction, 4, divided by, 5, end fraction of a tank of fuel in his car. He uses \dfrac{1}{10} 10 1 start fraction, 1, divided by, 10, end fraction of a tank per day. How many days will his fuel last? 10
Answers
Answer:
8 days
Step-by-step explanation:
We are told in the question:
Carlos has 4/5 of a tank of fuel in his car. He uses 1/10 of a tank per day.
How many days will his fuel last?
1/10 of fuel = 1 day
4/5 of fuel = x
Cross Multiply
1/10 × x = 4/5 × 1
x = 4/5 / 1/10
x = 4/5 ÷ 1/10
x = 4/5 × 10/1
x = 8 days
His fuel lasts for 8 days
Answer:
His fuel will last 8 days
Step-by-step explanation:
i got it right on khan academy
what equation represents this sentence? 28 is the quotient of a number and 4. responses 4=n28 4 equals n over 28 28=n4 28 equals n over 4 28=4n 28 equals 4 over n 4=28n 4 equals 28 over n
Answers
The equation that represents the sentence "28 is the quotient of a number and 4" is 28 = n/4.
In the given sentence, "28 is the quotient of a number and 4," we can break down the sentence into mathematical terms. The term "quotient" refers to the result of division, and "a number" can be represented by the variable "n." The divisor is 4.
1) Define the variable.
Let's assign the variable "n" to represent "a number."
2) Write the equation.
Since the sentence states that "28 is the quotient of a number and 4," we can write this as an equation: 28 = n/4.
The equation 28 = n/4 represents the fact that the number 28 is the result of dividing "a number" (n) by 4. The left side of the equation represents 28, and the right side represents "a number" divided by 4.
To know more about equation refer here:
https://brainly.com/question/29657983
#SPJ11
Please helpppp !!! Write this in y=Mx+b form

Answers
Answer:
y =(-3/2)x
Step-by-step explanation:
(0,0) ; (2 , -3)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(= \frac{-3-0}{2-0}\\\\= \frac{-3}{2}\)
Equation: y - y1 =m(x-x1)
y - 0 = \(\frac{-3}{2}(x- 0)\\\)
\(y = \frac{-3}{2}x\)
You will have no Y value because Y represents the Y-intercept, which, in this case is 0.
(0)
Suppose you buy a package every day. Suppose that there are c different types of objects and
each package contains one of those objects. A package is equally likely to contain any of the
c objects. Find the expected number of days that elapse before you have a full set of objects.
Answers
This sum is known as the harmonic series, and it grows approximately as the natural logarithm of c. Therefore, we can approximate E(X) as c * ln(c).
To find the expected number of days that elapse before you have a full set of objects, we can use the concept of the coupon collector's problem.
In the coupon collector's problem, imagine you are collecting coupons from a set of c different types. Each day, you buy a package and receive one coupon, which is equally likely to be any of the c types. The goal is to collect at least one coupon of each type.
Let's denote the random variable X as the number of days it takes to collect a full set of objects. To find the expected value E(X), we need to sum up the probabilities of each possible number of days.
On the first day, you have no coupons, so the probability of getting a new type of coupon is 1. The probability of getting a duplicate coupon is 0 since you have none yet. So, on the first day, the expected number of new types collected is c/c = 1.
On the second day, the probability of getting a new type of coupon is (c-1)/c since you already have one type. The probability of getting a duplicate coupon is 1/c since any of the c types is equally likely. So, on the second day, the expected number of new types collected is (c-1)/c + 1/c.
Similarly, on the third day, the expected number of new types collected is (c-2)/c + 2/c, and so on.
Generalizing this pattern, on the k-th day, the expected number of new types collected is (c-k+1)/c + (k-1)/c.
To find the expected number of days until a full set is collected, we sum up the expected number of new types collected each day until we reach c. Therefore, we have:
E(X) = 1 + (c-1)/c + 1/c + (c-2)/c + 2/c + ... + 1/c
Simplifying this expression, we get:
E(X) = c(1/c + 2/c + ... + 1/c) = c(1 + 1/2 + ... + 1/c)
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
1) Suppose that a group of U.S. election reformers argues that switching to a system based on proportional representation (PR) would significantly increase turnout. Skeptics claim that the reform would not have a significant effect on turnout. The following table, which reports mean turnouts and accompanying standard errors for PR and non-PR countries, will help you determine which side— the reformers or the skeptics— is more correct.Electoral system Mean turnout Standard errorPR 69.5 1.9Non-PR 61.2 1.7a) State the null hypothesis for the relationship between type of electoral system (PR/ non-PR) and turnout.b) (i) Calculate and write down the 95 percent confidence intervals for turnouts in PR and non-PR countries. (ii) Based on a comparison of the 95 percent confidence intervals, should the null hypothesis be rejected or not be rejected? (iii) Explain how you know.c) (i) Calculate and write down the mean difference between PR and non-PR countries. (ii) What is the standard error of the difference between the PR mean and the non-PR mean? (iii) Does the mean difference pass the eyeball test of significance? (iv) Explain how you know.
Answers
a. null hypothesis \(H_0\): PRmean=non-PRmean
b. the sample mean lies in the interval, so we fail to reject null hypothesis
c. critical value z(0.05)=1.96 is less than calculated z=3.56 so we fail to accept null hypothesis.
What is null hypothesis?A null hypothesis states that there is no statistical significance to be discovered in the set of presented observations. The validity of a theory is assessed through hypothesis testing on sample data. Sometimes known as the "null," it is represented by the symbol \(H_0\).
(a)
null hypothesis \(H_0\): PRmean=non-PRmean
(b).
i. \((1-\alpha)\times 100\%\) confidence interval for sample
\(mean=mean \pm z(\frac{\alpha }{2} )*SE(mean)\)
95% confidence interval for sample PRmean=PRmean±z(.05/2)*SE(mean)=69.5±1.96*1.9
=69.5±3.724=(65.776,73.224)
95% confidence interval for sample non-PRmean=non-PRmean±z(.05/2)*SE(mean)=61.2±1.96*1.7
=69.5±3.332=(57.868, 64.532)
ii. null hypothesis not be rejected
iii. since the sample mean lies in the interval, so we fail to reject null hypothesis
(c).
i. mean difference=69.5-61.5=8
ii. SE(difference)=\(\sqrt{SE(PR)^2+SE(non-PR)^2}\)
\(=\sqrt{1.9\times 1.9+1.2\times 1.2}\)
=2.2472
iii. we use z-test and z=(mean difference)/SE(difference)=8/2.2472=3.56
iv. here level of significance alpha is not mentioned,
let \(\alpha\) =0.05
critical value z(0.05)=1.96 is less than calculated z=3.56 so we fail to accept null hypothesis.
To know more about null hypothesis, visit:
https://brainly.com/question/4436370
#SPJ1
What is the numerical coefficient in the polynomial 4y+ 6?
Answers
Answer:
4y
Step-by-step explanation:
A coefficient is a number with a variable and no sign in between them.
The numerical coefficient in the polynomial 4y+ 6 is 4.
What is expression?A mathematical expression is a phrase that has a minimum of two numbers or variables and at least one mathematical operation. Let's examine the writing of phrases. The other number is x, and a number is 6 greater than half of it. In a mathematical expression, this proposition is denoted by the equation x/2 + 6.
A mathematical operation such as subtraction, addition, multiplication, or division is used to combine terms into an expression. In a mathematical expression, the following terms are used:
An absolute numerical number is referred to as a constant.Variable: A symbol without a set value is referred to as a variable.Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.Coefficient: A coefficient is a number that is multiplied by a variable in an expression.Given expression:
4y + 6
As, A coefficient is a number that is multiplied by a variable in an expression.
here the term that contain variable is 4y.
So, the coefficient is 4.
Hence, the numerical coefficient in the polynomial 4y+ 6 is 4.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ2
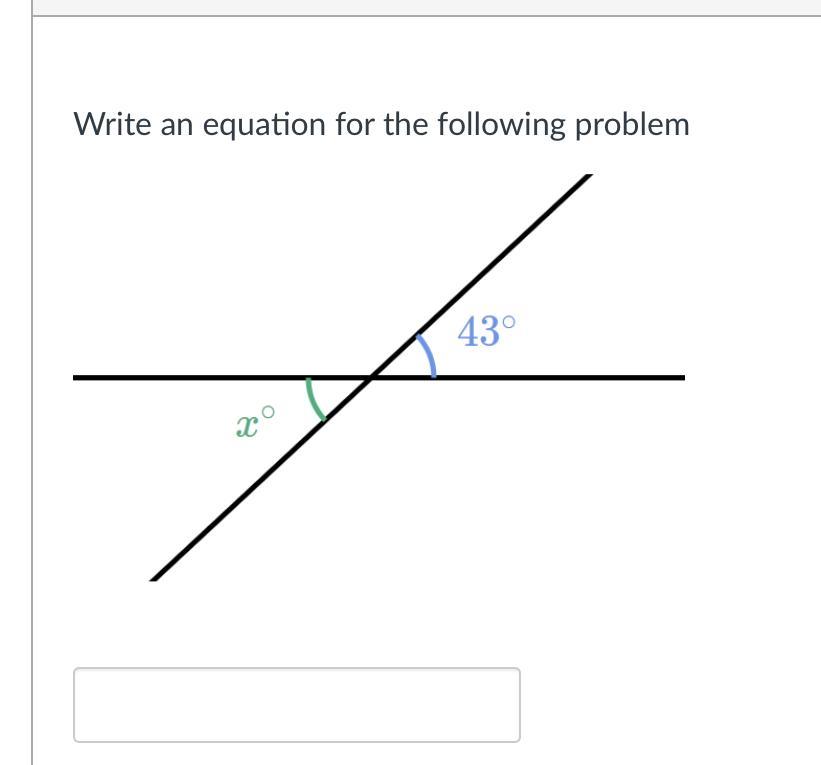
i don't know just someone answer this for me thanks
Answers
Answer:
the answer would be 43 degrees.
Step-by-step explanation:
∂²p/∂r² + 1/r ∂p/∂r = ϕμC/k ∂p/∂t
derivation of equations
1-partial derivative diffusivity equation spherical flow
2- partial derivative diffusivity equation hemi- spherical flow
Answers
The partial derivative diffusivity equation for spherical flow is ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t, and for hemispherical flow, it is the same equation.
1. The partial derivative diffusivity equation for spherical flow is derived from the spherical coordinate system and applies to radial flow in a spherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
2. The partial derivative diffusivity equation for hemispherical flow is derived from the hemispherical coordinate system and applies to radial flow in a hemispherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
1. For the derivation of the partial derivative diffusivity equation for spherical flow, we consider a spherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the polar angle (φ). By assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in spherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
2. Similarly, for the derivation of the partial derivative diffusivity equation for hemispherical flow, we consider a hemispherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the elevation angle (ε). Again, assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in hemispherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
In both cases, the term ϕμC/k ∂p/∂t represents the source or sink term, where ϕ is the porosity, μ is the fluid viscosity, C is the compressibility, k is the permeability, and ∂p/∂t is the change in pressure over time.
These equations are commonly used in fluid mechanics and petroleum engineering to describe radial flow behavior in spherical and hemispherical geometries, respectively.
To learn more about partial derivative, click here: brainly.com/question/2293382
#SPJ11
Given f (g (x)) = x + 4 and f (x) = 3x + 5, find g (x).
Answers
Answer:
g(x) = \(\frac{1}{3}(x - 1) = \frac{x}{3} - \frac{1}{3}\)
Step-by-step explanation:
f(x) = 3x + 5
f[g(x)] = 3[g(x)] + 5
⇒ 3[g(x)] + 5 = x + 4
⇒ 3[g(x)] = x + 4 - 5
⇒ 3[g(x)] = x - 1
⇒ g(x) = \(\frac{1}{3}(x - 1) = \frac{x}{3} - \frac{1}{3}\)
The sail of a boat is in the shape of a right triangle. which expression shows the length, in meters, of the sail? the sail of a boat is a right triangle with an acute angle at the tip equal to 50 degrees and the side of the sail which is the hypotenuse to the right triangle is 7 meters long. 7(tan 50°) 7(sin 50°) tangent 50 degrees over 7 sine 50 degrees over 7
Answers
The expression for the length of the sail is x = 7( tan 50° ).
According to the given question.
The sail of a boat is in the shape of a right triangle.
And, the sail of a boat is a right triangle with an acute angle at the tip equal to 50 degrees and the side of the sail which is the hypotenuse to the right triangle is 7 meters long.
Now, the side that measures 7 meters would be the adjacent because its right next to the angle and its not the hypotenuse because its not the largest side
And, the side which we do not know the length to will be the opposite side because it is opposite from where the angle is.
So, we have the the measure of the adjacent side and the angle of the tip. And we have to find the expression for the length of the sail.
Let the length of the sail be x meters.
Now, in the given right angled triangle
We can say that
tan A = Opposite side/Adjacent side
⇒ tan 50° = x/7
⇒ x = 7( tan 50° )
Hence, the expression for the length of the sail is x = 7( tan 50° ).
Find out more information about expression here:
https://brainly.com/question/28172855
#SPJ4
Consider the following.
x' =
1 2
−5 −1
x
(a) Express the general solution of the given system of equations in terms of real-valued functions.
(b) Also draw a direction field and sketch a few of the trajectories.
(c) Describe the behavior of the solutions as
t → [infinity].
Answers
(A - 3I)v = | -2 2 | | v1 | = | 0 |
| -5 -4 | | v2 | | 0 |
Solving the system of equations, we obtain v1 = 1 and v2 = 1. The general solution of the given system of equations is: x(t) = C1 * e^(3t) * [1, 1]^T
where C1 is an arbitrary constant and T denotes the transpose operation.
(b) As a question-answering bot, I am unable to draw images. However, I can guide you on how to draw the direction field and sketch the trajectories. Plot the vector field F(x, y) = Ax, where A is the given matrix, and observe the behavior of the field. The eigenvector [1, 1] will provide the direction for the trajectories. Since the eigenvalue is positive, the trajectories will be moving away from the origin along the direction of the eigenvector.
(c) As t → ∞, the solutions of the system will grow exponentially in the direction of the eigenvector [1, 1]. Since the eigenvalue is positive (λ1 = 3), the trajectories will move away from the origin along the line y = x.
The given system of equations can be expressed as x' = Ax, where A is the coefficient matrix:
A =1 2
−5 −1
(a) The general solution of the system can be found by solving for the eigenvalues and eigenvectors of the matrix A. The eigenvalues of A can be found by solving the characteristic equation:
det (A - λI) = 0
⇒ det (1-λ 2-5 -1-λ) = 0
⇒ (1-λ)(-1-λ) - 2(-5) = 0
⇒ λ^2 + λ - 9 = 0
⇒ λ = (-1 ± sqrt(37)i)/2
Since the eigenvalues are complex, the general solution of the system can be expressed in terms of real-valued functions using Euler's formula:
x(t) = c1 e^(αt) cos(βt) v1 + c2 e^(αt) sin(βt) v2
where α = -1/2, β = sqrt(37)/2, v1 and v2 are the real and imaginary parts of the eigenvector corresponding to the eigenvalue (-1 + sqrt(37)i)/2, and c1 and c2 are arbitrary constants determined by the initial conditions.
(b) To draw a direction field, we can plot arrows on a grid that indicate the direction of the vector x' = Ax at various points in the xy-plane. The direction of the vector at each point (x,y) can be found by evaluating Ax at that point and plotting an arrow with a slope equal to the components of Ax. To sketch a few trajectories, we can use the general solution and choose different initial conditions to plot several curves in the xy-plane. The trajectories will follow the direction of the arrows in the direction field.
(c) As t → infinity, the behavior of the solutions depends on the eigenvalues of A. Since the real part of the eigenvalue with a larger magnitude is negative (-1/2), the solutions will approach the origin as t → infinity. The imaginary part of the eigenvalue will cause oscillations in the trajectories, which become more and more damped as t increases.
Learn more about Equation:
brainly.com/question/29538993
#SPJ11