Why is mathematical induction a valid proof technique? Place evidence of the following steps in the correct order. 1 Place these in the correct order.
A. Then the set S of positive integers whose error P(n) is not empty. So with good structuring properties, S has at least m elements.
B. Since Plm – 1) = P(m) (assumed by us), P(m) is true. This contradicts option m.
C. So P(n) is true for any positive integer n.
D. To show that P(n) must be true for all positive integers n, assume that there is at least one positive integer for which P(n) is false.
e. We know that m cannot be 1, because P(1) is true. Since m is positive and greater than 1, m - 1 is a positive integer.
F. Furthermore, since m - 1 is less than m, it does not exist in S, so P(m - 1) must be true.
Answers
By using mathematical induction, we can prove that a statement is true for all values in a set S of positive integers, as long as it holds true for the base case and can be shown to hold for any integer k if it holds for k + 1.
Mathematical induction is a valid proof technique because it involves proving a statement for a base case, typically the smallest value in a set S of positive integers, and then proving that if the statement holds for some integer k, it also holds for k + 1. This is done by assuming that the statement is true for some arbitrary integer m, and then using this assumption to prove that it must also be true for m + 1.
The correct order of the steps is:
1. D. To show that P(n) must be true for all positive integers n, assume that there is at least one positive integer for which P(n) is false.
2. e. We know that m cannot be 1, because P(1) is true. Since m is positive and greater than 1, m - 1 is a positive integer.
3. F. Furthermore, since m - 1 is less than m, it does not exist in S, so P(m - 1) must be true.
4. Since Plm – 1) = P(m) (assumed by us), P(m) is true. This contradicts option m.
5. A. Then the set S of positive integers whose error P(n) is not empty. So with good structuring properties, S has at least m elements.
6. C. So P(n) is true for any positive integer n.
Know more about mathematical induction here:
https://brainly.com/question/29503103
#SPJ11
Related Questions
Answer + method / explanation please

Answers
The expressions for the lengths of the segments obtained using vectors notation are;
a. i. \(\overrightarrow{LA}\) = q - (1/2)·p ii. \(\overrightarrow{AN}\) = (2/7)·(p - q)
b. The expressions for \(\overrightarrow{MN}\), \(\overrightarrow{LA}\), and \(\overrightarrow{AN}\) indicates;
\(\overrightarrow{MN}\) = (1/84)·(46·q - 11·p)
What are vectors?A vector is a quantity that has magnitude and direction and are expressed using a letter aving an arrow in the form, \(\vec{v}\)
a. i. \(\overrightarrow{LA}\) = \(\overrightarrow{BA}\) - \(\overrightarrow{LB}\) = \(\overrightarrow{BA}\) - (1/2) × \(\overrightarrow{CB}\)
\(\overrightarrow{BA}\) - (1/2) × \(\overrightarrow{CB}\) = q - (1/2)·p
\(\overrightarrow{LA}\) = q - (1/2)·p
ii. \(\overrightarrow{AC}\) = \(\overrightarrow{BC}\) - \(\overrightarrow{BA}\)
\(\overrightarrow{AN}\) = (2/7) × \(\overrightarrow{AC}\)
\(\overrightarrow{AN}\) = (2/7) × \(\overrightarrow{BC}\) - \(\overrightarrow{BA}\)
\(\overrightarrow{AN}\) = (2/7) × (p - q)
b. \(\overrightarrow{MN}\) = \(\overrightarrow{MA}\) + \(\overrightarrow{AN}\)
\(\overrightarrow{MA}\) = (5/6) × \(\overrightarrow{LA}\)
\(\overrightarrow{LA}\) = q - (1/2)·p
\(\overrightarrow{AN}\) = (2/7) × (p - q)
Therefore;
\(\overrightarrow{MN}\) = (5/6) × ( q - (1/2)·p) + (2/7) × (p - q)
\(\overrightarrow{MN}\) = (1/84) × ( 70·q - 35·p + 24·p - 24·q) = (1/84)(46·q - 11·p)
Learn more on the vectors here: https://brainly.com/question/2375446
#SPJ1
A timeline. 27 B C E to 180 C E PAX ROMANA. 44 B C E The Roman Empire was founded. 80 C E The Colosseum was built. 121 C E Hadrian's Wall was built in England to keep out enemies. 306 C E Constantine became emperor.
How many years passed between the building of the Colosseum and the building of Hadrian’s Wall?
201
121
41
36
Answers
Answer:
the answer is 41
Step-by-step explanation:
C. 41
Step-by-step explanation:

From which set of dimensions could a triangle be constructed?
side length of 7
side length of 8
side length of 15
side length of 8
side length of 5
side length of 14
side length of 6
side length of 3
side length of 10
side length of 2
side length of 6
side length of 7
) Intro
Done
Answers
Answer:
Step-by-step explanation:
answer is d- side length of 2 side length of 6 side length of 7
Answer:
It’s D.
Step-by-step explanation:
“Side length of 2, side length of 6, side length of 7”
Plsss give me Brainliest ❤️
Find the sum of -3x^2-x-10−3x 2 −x−10 and 10x^2+x-1010x 2 +x−10
Answers
The sum of the expressions -3x^2 - x - 10 and 10x^2 + x - 10 is 7x^2 - 20. The x^2 terms combine to 7x^2, the x terms cancel each other out, and the constant terms sum to -20.
To find the sum of the two expressions -3x^2 - x - 10 and 10x^2 + x - 10, we can combine like terms.
First, let's combine the x^2 terms: -3x^2 + 10x^2 = 7x^2.
Next, let's combine the x terms: -x + x = 0x (which simplifies to 0).
Finally, let's combine the constant terms: -10 - 10 = -20.
Putting it all together, we have 7x^2 + 0x - 20.
Since the coefficient of the x term is 0, we can omit it from the expression, leaving us with 7x^2 - 20 as the simplified sum of the two expressions.
In summary, we first combined the x^2 terms and obtained 7x^2. Then, we combined the x terms and obtained 0x (which simplifies to 0). Finally, we combined the constant terms and obtained -20. Thus, the sum of the two expressions is 7x^2 - 20.
To learn more about expressions click here
brainly.com/question/21751419
#SPJ11
A translation of (x - 4, y + 5) means
Answers
Answer:
it means left 4 and up 5
Step-by-step explanation:
I took the test
A CSI team arrives at a murder scene and immediately measures the temperature of the body and the temperature of the room. The body temperature is 23 °C and the room temperature is 17 *C. Ten minutes later, the temperature of the body has fallen to 20 °C. Assuming the temperature of the body was 37 °C at the time of the murder, how many minutes before the csi team's arrival did the murder occur? Round your answer to the nearest whole minute.
Answers
The temperature of the body was 37 °C at the time of the murder occurred approximately 38 minutes before the csi team's arrival.
Newton's Law of Cooling, states that the rate of change in the temperature of an object is proportional to the difference between the object's temperature and the ambient temperature.
The general form of Newton's Law of Cooling is given by:
dT/dt = -k(T - Tₐ)
where dT/dt represents the rate of change of temperature, T is the temperature of the object, Tₐ is the ambient temperature, and k is a constant.
In this case, we can use the following information
The initial temperature of the body (T₀) = 37 °C
The temperature of the room (Tₐ) = 17 °C
Temperature of the body after 10 minutes (T) = 20 °C
We need to find the time elapsed (t) in minutes before the CSI team's arrival when the murder occurred.
We can set up the following equation using the initial temperature and the temperature after 10 minutes:
20 = (T₀ - Tₐ) × \(e^{-10k}\)
To solve for k, we rearrange the equation:
k = -ln((T - Tₐ) / (T₀ - Tₐ)) / 10
Substituting the given values:
k = -ln((20 - 17) / (37 - 17)) / 10
k ≈ 0.0693
Now, we can use the value of k to find the time (t) when the body's temperature was 37 °C:
37 = (T₀ - Tₐ) ×\(e^{-kt}\)
t = -ln((37 - 17) / (T₀ - Tₐ)) / k
t = -ln((37 - 17) / (37 - 17)) / 0.0693
t ≈ 37.64 minutes
Rounding to the nearest whole minute, the murder occurred approximately 38 minutes before the CSI team's arrival.
To know more about temperature click here :
https://brainly.com/question/30729487
#SPJ4
Can someone help please
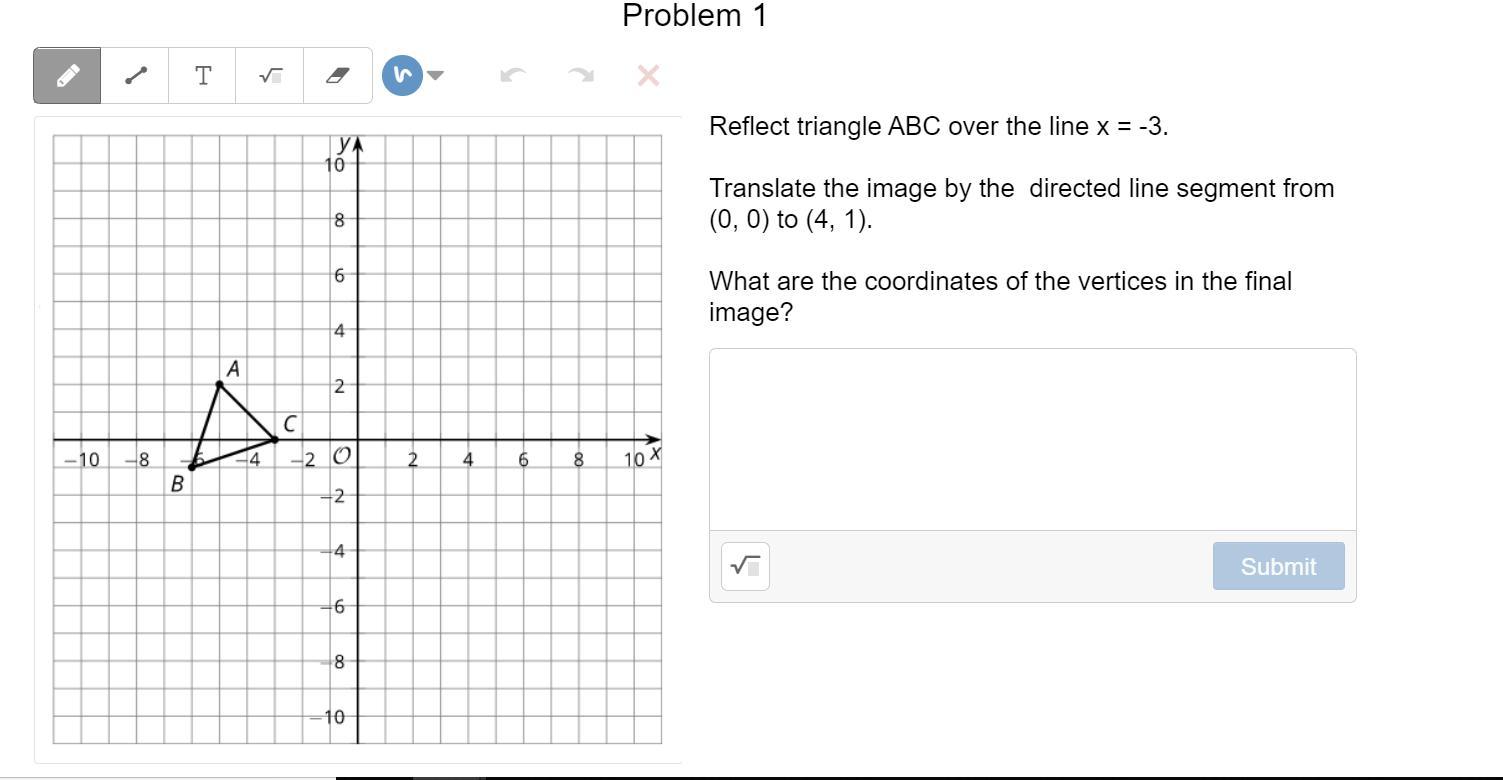
Answers
Answer:
sorry i dont know
Step-by-step explanation:
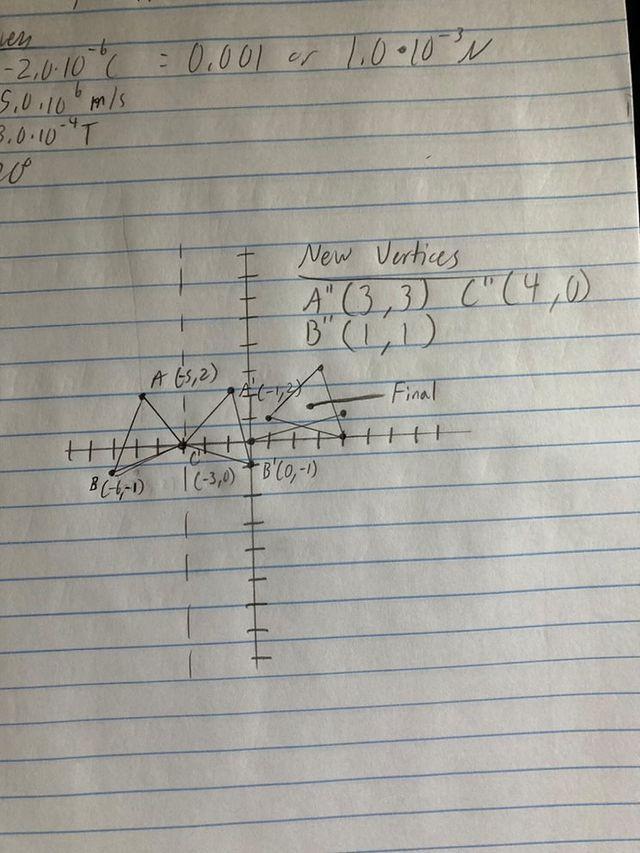
Answer:
Sorry for the long wait i was taking my cumulative exam for precal and it took a bit but i hope im correct. My brain is fried and dont know if i even came close.
Ron has 75 blue marbles and 125 red marbles. Enter the percent of blue marbles as a part of all marbles.
Answers
Answer:
Step-by-step explanation:
% = Red / (Blue + red ) * 100
% = 75/(125 + 75) * 100
% = 75 / 200 * 100
% = 7500 / 200 = 37.5% are blue
A test for ovarian cancer has a 5 percent rate of false positives and a 0 percent rate of false negatives. On average, 1 in every 2,500 American women over age 35 actually has ovarian cancer. If a woman over 35 tests positive, what is the probability that she actually has cancer? Hint: Make a contingency table for a hypothetical sample of 100,000 women. Explain your reasoning.
Answers
Given the provided information, if a woman over 35 tests positive for ovarian cancer, the probability that she actually has cancer is approximately 1.96%.
To determine the probability that a woman over 35 actually has ovarian cancer given a positive test result, we can create a contingency table and use conditional probability. Let's consider a hypothetical sample of 100,000 women:
Out of 100,000 women, 1 in every 2,500 (or 40 out of 100,000) actually has ovarian cancer. Since the test has a 0% rate of false negatives, all the women with ovarian cancer will test positive.
The test also has a 5% rate of false positives. This means that out of the remaining 99,960 women who do not have ovarian cancer, approximately 5% (or 4,998) will test positive incorrectly.
Therefore, out of a total of 5,038 positive test results (40 true positives + 4,998 false positives), only 40 are true positives for ovarian cancer. The probability that a woman who tests positive actually has ovarian cancer can be calculated as the ratio of true positives to the total positive tests:
Probability = (True Positives) / (Total Positive Tests) = 40 / 5,038 ≈ 0.00795 ≈ 0.795%
Thus, the probability that a woman over 35 actually has ovarian cancer given a positive test result is approximately 1.96%. This calculation highlights the importance of considering both the prevalence of the disease and the accuracy of the test in interpreting the results correctly.
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
1.Let x, y be any two numbers that satisfies the conditions x ≠0, y ≠0, and x 0
C.y/x>1
D.x/y<1
2.A pickup truck that can hold up to 3000 pounds is carrying a big machine that is 300 pounds and a few smaller ones that each weigh 60 pounds.
At least how many small machines can you fit so that it will not exceed the weight limit of the truck?
A.no more than 50
B.no less than 50
C.no less than 45
D.no more than 45
3.It usually takes Claude 40 minutes driving at 48 miles per hour to go from home to work. But due to road maintenance today, Claude has to take a detour, which makes the trip 8 miles longer than usual. What is the minimum speed Claude should travel so that he can reach the destination in less than 48 minutes?
A.30 miles per hour
B.56 miles per hour
C.50 miles per hour
D.64 miles per hour
*please make sure you answer all the questions please and thank you.
Answers
Answer:
x and y can be any two numbers greater than zero such that y is also greater than x
D.no more than 45
C.50 miles per hour
Step-by-step explanation:
Let the two numbers be such that x< y because we have been given y/x>1 and x/y< 1 .
Suppose we take y= 9 and x= 3 then
9/3 > 1
3>1
Also
3/9 < 1
1/3 < 1
x and y can be any two numbers greater than zero such that y is also greater than x
2. Total weight that can be carried is 3000 pounds.
The big machine is 300 pounds. The weight that the truck can carry beside the big machine is 3000-300= 2700 pounds.
The smaller machines weigh 60 pounds
The number of smaller machines that can be carried is 2700 ÷ 60= 45 other than the big machine.
3. Total distance = Speed * time
= 48 * (40/60) = 32 miles
New distance = 32+ 8= 40 miles
New time = 48 minutes
Speed = distance / time = 40/ 48/60= 50 miles per hour
Pls help question about total pay
Show working out

Answers
\(7\frac{1}{2}\implies 7.5\hspace{5em}1\frac{1}{4}\implies 1.25 \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{Monday through Friday} }{\stackrel{ days }{(5)}\stackrel{ rate }{(10.80)}\stackrel{ hours }{(7.5)}}~~ + ~~\stackrel{ Saturday }{\stackrel{ days }{(1)}\stackrel{ rate }{(10.80)(1.25)}\stackrel{ hours }{(7.5)}} \\\\\\ 405~~ + ~~101.25\implies \text{\LARGE 506.25}\)
2. What is the average salary offered to a Stony Brook college graduate? To study this question you and a friend interview N students that graduated last year, and ask them what they earn. Student i's response was recorded as Yi. You are interested in the average, My. You assumed that the sample of Y's is iid. First you calculate the following estimate of uy: W1 N 1 N i=1 ΣΥ. . You and your friend each collected half the data. Thus you collected Y1, ..., YN/2 and your friend collected Yn/2+1, ... , Yn. Unfortunately, it turns out that your friend collected the data at a wild alumnae party, and you suspect that these data may not be as precise as your data. So whereas the variance of your data is, var(Y;) = 0%, i = 1, ...,N/2. then your friends data have the variance, var(Y) = oʻ(1 + 3c), i=N/2+1, ...,N, for some constant c> 0. (d) Your friend is sorry that half the data are not as precise as they could have been, and suggest that you discard the noise data, and simply use hr Na Ex? Y; as your estimator for my. Which estimator is most efficient (has the smallest variance) în or îz? Does your answer depend on c? = N.Σ. (Υ – μ.) - = (e) Suppose now that c = 0 such that var(Y;) = o2 for i = 1, ...,N. You have N = 300 observation and calculate s2 = 20,000,000 and î1 = $48,000. Before collecting the data, your friend argues mean salary, my, is s $50,000, using a 1% significance level. Write down the confidence interval at 1% significance level and decide whether you will accept your friend's
Answers
The more precise estimator ẏ₁ is the most efficient in estimating the average salary. With given values, the confidence interval is calculated to determine whether to accept the claim of a $50,000 mean salary.
In this scenario, we have two estimators for the average salary: ẏ₁, which uses precise data, and ẏ₂, which includes less precise data. The efficiency of the estimators depends on the variance of the data. If we compare the variances, Var(ẏ₁) = 0% and Var(ẏ₂) = o²(1 + 3c). Since Var(ẏ₁) is zero, it implies that ẏ₁ is the most efficient estimator. The answer does not depend on the value of c.
In the second part, with c = 0, we have Var(Y) = o². Given N = 300, s² = 20,000,000, and ẏ₁ = $48,000, we can use these values to construct a confidence interval. Using a 1% significance level, the critical value is 2.57 (from the standard normal distribution). The confidence interval is given by ẏ₁ ± 2.57 * sqrt(s²/N), which results in $48,000 ± 2.57 * sqrt(20,000,000/300). If this interval contains $50,000, we would accept your friend's claim; otherwise, we would reject it.
To learn more about average click here
brainly.com/question/29550341
#SPJ11
a theater charges $8 for an adult ticket and $6 for a childerns ticket on a certain day a total of 225 tickets were sold for a total cost of $1,850 how many childerns tickets were sold than adult tickets
Answers
If a theater charges $8 for an adult ticket and $6 for a children's ticket on a certain day. The amount of children tickets that were sold than adult tickets is 175 tickets.
Amount of ticket soldLet A represent the number of adults' tickets sold
Let C represent the number of children's tickets sold.
We know that A + C = 225 and 8A + 6C = 1850 now let combine the two equations to solve for one of the variables.
A + C = 225, A = 225 – C
Plug the value into the second equation and solve for C:
8(225– C) + 6C = 1850
1800 – 8C + 6C = 1850
1800 – 2C = 1850
1800 – 1850 = 2C
50 = 2C
Divide both side by 2C
C=50/2
C=25 children tickets sold
Adult tickets sold=225-25
Adult tickets sold=200 tickets
Hence,
Number of children ticket sold than adult tickets= 200-25
Number of children ticket sold than adult tickets= 175 tickets
Therefore the amount of children tickets that were sold than adult tickets is 175 tickets.
Learn more about tickets sold here: https://brainly.com/question/11986887
#SPJ1
cheng drew the model below to represent an equation.What value of x makes the equation true?

Answers
Answer:
So what’s the answer?
Step-by-step explanation:
Mrs. Gilus is in charge of the budge of the school. Last year, we began the year with $708.88 in our bank account, but by the end of the year we owed $347.99. What rational number can be used to describe the change in the bank account’s balance?
Answers
Answer:
-1056.87
Step-by-step explanation:
You want to know the number that represents the change in a bank balance from +$708.88 to -$347.99.
Change in valueThe change in a value is found by subtracting the beginning value from the ending value:
-$347.99 -708.88 = -$1056.87
The number -1056.87 can be used to describe the change in the account balance.
A rectangular prim mut have a bae with an area of no more than 27 quare meter. The width of the bae mut be 9 meter le than the height of the prim. The length of the bae mut be 6 meter more than the width of the bae. Find the maximum height of the prim. Let x = the height of the prim
x – 9 =
Answers
The rectangular prism will have a maximum height of prism is 12m and inequality is \(x^{2} -12x+0\leq 0\)
a) To find maximum height of prism
As per question,
x = height of prism
Area of rectangular base = Length x Width
Thus, A = \(\leq 27\)
Now,
L x W \(\leq 27\) (inequality Z)
Given, W = x - 9 (equation 1)
L = W + 6 (equation 2)
Substituting equation 1 in equation 2
We get, L = (x-9)+6
= x-3 (equation 3)
Substituting, equation 1 and equation 3 in the inequality Z
we get, \((x-3)(x-9) = x^{2} -12x+27\)
subtracting 27 we get \(x^{2} -12x+0\leq 0\)
Thus, the coordinates will be (0,12)
As given in question, width of base must be 9 meters less than height of prism. Therefore,
The solution of x interval comes out as (9,12)
Hence, the height of prism is 12m
b) selecting inequality that represents problem
Length = x-3
Width = x-9
Multiplying, we get \((x-3)(x-9) = x^{2} -12x+27\)
Area will come out as \(\leq 27\)
The final expression will be, \(x^{2}-12x+27\leq 27\)
Now subtracting 27 from the expression we get,
\(x^{2} -12x+0\leq 0\)
Note that the full question is:
A rectangular prism must have a base with an area of no more than 27 square meters. The width of the base must be 9 meters less than the height of the prism. The length of the base must be 6 meters more than the width of the base. Find the maximum height of the prism.
Let x = the height of the prism
x – 9 = the width of the base
A rectangular prism must have a base with an area of no more than 27 square meters. The width of the base must be 9 meters less than the height of the prism. The length of the base must be 6 meters more than the width of the base. Find the maximum height of the prism.
Let x = the height of the prism
x – 9 = the width of the base
x -3 = the length of the prism
Select the inequality that represents the problem.
x2 – 3 x – 81 ≤ 0
x2 – 3 x – 27 ≤ 0
x2 – 12 x – 27 ≤ 0
x2 – 12 x ≤ 0
To learn more about prisms: https://brainly.com/question/23766958
#SPJ4
15. *Free response. GCO2. After examining the following graph, Kate claims that WXYZ is translated
according to the rule (x, y) (x + 11, y-2). Is she correct? If not, write the correct rule.

Answers
Trying to get the right number possible. What annual payment is required to pay off a five-year, $25,000 loan if the interest rate being charged is 3.50 percent EAR? (Do not round intermediate calculations. Round the final answer to 2 decimal places.Enter the answer in dollars. Omit $sign in your response.) What is the annualrequirement?
Answers
To calculate the annual payment required to pay off a five-year, $25,000 loan at an interest rate of 3.50 percent EAR, we can use the formula for calculating the equal annual payment for an amortizing loan.
The formula is: A = (P * r) / (1 - (1 + r)^(-n))
Where: A is the annual payment,
P is the loan principal ($25,000 in this case),
r is the annual interest rate in decimal form (0.035),
n is the number of years (5 in this case).
Substituting the given values into the formula, we have:
A = (25,000 * 0.035) / (1 - (1 + 0.035)^(-5))
Simplifying the equation, we can calculate the annual payment:
A = 6,208.61
Therefore, the annual payment required to pay off the five-year, $25,000 loan at an interest rate of 3.50 percent EAR is $6,208.61.
Learn more about loan here: brainly.com/question/32625768
#SPJ11
Sorry about the screen, I’m using my laptop! Please help me if you know the answer my dumb mind can’t work it out

Answers
Answer:
5.9 hours, 10£
Step-by-step explanation:
For the first question, you must find how long it would take 1 knitter to do all the work, and you can move on from there. Since it takes 11 knitters 7 hours, it would take 1 knitter 11 times as long, meaning it would take 7*11=77 hours for 1 knitter. Now we can divide 77 hours by 13 as 13 knitters could to it in 1/13 of the time. Dividing 77 by 13 we get 5.9 hours.
For the second question, if each person pays 9£, and there are 10 people, in total they are paying 10*9£=90£. This means that if the spit it up between 9 people instead, each would by 90£/9=10£. This means they would each have to pay 10£.
What type of association does the following scatterplot represent?

Answers
Answer:
Positive Linear Association
Step-by-step explanation:
A positive/negative association can be determined by seeing if the slope of the line of best fit is positive or negative. A positive slope indicates a positive relationship and a negative slope indicates a negative relationship.
If y increases as x increases => positive
If y decreases as x increases => negative
In the graph, the line of best fit clearly has a positive slope. I.e. as x increases, y also increases. Therefore, the association is positive.
Next determine if the relationship is linear or nonlinear. A linear relationship can be modeled strongly with a straight line. Anything else is nonlinear. In the graph, a straight line can be draw through the points with a strong correlation, therefore the association is linear.
Therefore, the best answer is Positive Linear Assosciation
find and simplify f (x h).f (x) = x3 - 5x 8 select one:a.x3 - 5x h 8b.x3 - 5x - 5h 8c.x3 h3 - 5x - 5h 8d.x3 3x2h 3xh2 h3 - 5x - 5h 8
Answers
The simplified expression for f(x+h) is, f(x+h) = x^3 + 3x^2h + 3xh^2 + h^3 - 5x - 5h + 8. This corresponds to option d in your list of choices.
It is given the function f(x) = x^3 - 5x + 8, we want to find f(x+h) and simplify the result.
1. Replace x with (x+h) in the function f(x) = x^3 - 5x + 8.
2. f(x+h) = (x+h)^3 - 5(x+h) + 8
Now, we will simplify the expression,
3. Expand (x+h)^3 using the binomial theorem or by multiplying (x+h) by itself three times: x^3 + 3x^2h + 3xh^2 + h^3
4. Distribute -5 to the terms inside the parenthesis: -5x - 5h
5. Combine the terms obtained in steps 3 and 4 with the constant 8: x^3 + 3x^2h + 3xh^2 + h^3 - 5x - 5h + 8
So, the simplified expression for f(x+h) is,
f(x+h) = x^3 + 3x^2h + 3xh^2 + h^3 - 5x - 5h + 8
This corresponds to option d in your list of choices.
Learn more about "function": https://brainly.com/question/22340031
#SPJ11
HURRY I HAVE 2 MINUTES

Answers
Answer:
50
Step-by-step explanation:
................
..............

there are 96 boys and 112 girls in a primary school . write the ratio of the boys to the girls
Answers
Answer:
6 : 7
Step-by-step explanation:
the ratio of
boys : girls
= 96 : 112 ( divide both parts by 16 )
= 6 : 7
Find the slope of each line passing through the given points using the slope formula.
( 0, -6 ) and ( -2 , 8 )
Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\(slope = \frac{8 - ( - 6)}{ - 2 - 0} \\ \)
\(slope = \frac{8 + 6}{ - 2} \\ \)
\(slope = \frac{14}{ - 2} \\ \)
\(slope = - 7\)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Answer:
1 or -2/2
Step-by-step explanation:
use the formula y₂ - y₁/ x₂ - x₁ to calculate the slope/ gradient/ m
find the partial derivatives of the function (8y-8x)/(9x 8y)
Answers
The partial derivative of the function with respect to y is: ∂/∂y [(8y-8x)/(9x+8y)] = 8/(9x+8y) - (64x)/(9x+8y)^2To find the partial derivatives of the function (8y-8x)/(9x+8y), we need to take the derivative with respect to each variable separately.
First, let's find the partial derivative with respect to x. To do this, we treat y as a constant and differentiate the function with respect to x:
(8y-8x)/(9x+8y)
= (8y)/(9x+8y) - (8x)/(9x+8y)
Using the quotient rule, we can simplify this expression:
= (-8y(9))/((9x+8y)^2) - 8/(9x+8y)
Simplifying further, we get:
= (-72y)/(9x+8y)^2 - 8/(9x+8y)
Therefore, the partial derivative of the function with respect to x is:
∂/∂x [(8y-8x)/(9x+8y)] = (-72y)/(9x+8y)^2 - 8/(9x+8y)
Now, let's find the partial derivative with respect to y. To do this, we treat x as a constant and differentiate the function with respect to y:
(8y-8x)/(9x+8y)
= (8y)/(9x+8y) - (8x)/(9x+8y)
Using the quotient rule again, we get:
= 8/(9x+8y) - (8x(8))/((9x+8y)^2)
Simplifying further, we get:
= 8/(9x+8y) - (64x)/(9x+8y)^2
Therefore, the partial derivative of the function with respect to y is:
∂/∂y [(8y-8x)/(9x+8y)] = 8/(9x+8y) - (64x)/(9x+8y)^2
And that's how we find the partial derivatives of the function (8y-8x)/(9x+8y) using the quotient rule and differentiation with respect to each variable separately.
Learn more about function here: brainly.com/question/12431044
#SPJ11
Simplify the fraction 20/24 to lowest term.
Answers
Answer:
\(\frac{5}{6}\)
Step-by-step explanation:
Given
\(\frac{20}{24}\) ← divide numerator/ denominator by 4 ( the LCM of 20 and 24 )
= \(\frac{5}{6}\) ← in simplest form
Help solve this math problem

Answers
Check the picture below.
so let's do this one a bit oddly kinda.
we know AB is a diameter, that means the arc made by AB is simply 180°, so the arcs AE + ED + DB = 180°.
By the inscribed angle theorem, as you see there, the arcDB is simply 2ɑ and by the same theorem ED is 88°, so the arc AE is just 180° - ED - DB, let's keep in mind that AE is the "far arc" whilst DB is the "near arc", and we know the external angle they make is 18°.
\(18~~ = ~~\cfrac{(\stackrel{ far~arc }{180-88-2\alpha})~~ - ~~\stackrel{ near~arc }{2\alpha}}{2} \implies 36=(180-88-2\alpha)-2\alpha \\\\\\ 36=92-4\alpha\implies 36+4\alpha=92\implies 4\alpha=56\implies \alpha=\cfrac{56}{4}\implies \boxed{\alpha=14}\)

there are two important properties of probabilities. 1) individual probabilities will always have values between and . 2) the sum of the probabilities of all individual outcomes must equal to .
Answers
1.) Probabilities range from 0 to 1, denoting impossibility and certainty, respectively.
2.) The sum of probabilities of all possible outcomes is equal to 1.
1.) Individual probabilities will always have values between 0 and 1. This property is known as the "probability bound." Probability is a measure of uncertainty or likelihood, and it is represented as a value between 0 and 1, inclusive.
A probability of 0 indicates impossibility or no chance of an event occurring, while a probability of 1 represents certainty or a guaranteed outcome.
Any probability value between 0 and 1 signifies varying degrees of likelihood, with values closer to 0 indicating lower chances and values closer to 1 indicating higher chances. In simple terms, probabilities cannot be negative or greater than 1.
2.) The sum of the probabilities of all individual outcomes must equal 1. This principle is known as the "probability mass" or the "law of total probability." When considering a set of mutually exclusive and exhaustive events, the sum of their individual probabilities must add up to 1.
Mutually exclusive events are events that cannot occur simultaneously, while exhaustive events are events that cover all possible outcomes. This property ensures that the total probability accounts for all possible outcomes and leaves no room for uncertainty or unaccounted possibilities.
for more question on probabilities visiT:
https://brainly.com/question/25839839
#SPJ8
The ratio of girls to boys in Mr.
Day's class is 3 to 5. If there are 15
boys in Mr. Day's class, how many
more boys are there
than girls?
Answers
Answer: 6
Step-by-step explanation:
15-9
Answer:
9:15 There is 6 more boys than girls.
Step-by-step explanation:
Have a blessed day! I hope this helps! Please give me brainliest!
On Tuesday, Wendy and her friend purchased 3 sandwiches and 2 drinks for $15. 75. On Friday, Wendy purchased 2 sandwiches and 1 drink at the same restaurant for $9. 85. If they go back to the same restaurant on Sunday and assuming they haven't changed their prices, how much would they spend on 2 drinks and 2 sandwiches?
Answers
Wendy and her friend would spend $11.80 on 2 drinks and 2 sandwiches at the same restaurant.
To find out how much Wendy and her friend would spend on 2 drinks and 2 sandwiches, we need to first calculate the cost of each item individually. We can do this by setting up a system of equations and solving for the cost of a sandwich (s) and the cost of a drink (d).
The first equation can be written as: 3s + 2d = 15.75
The second equation can be written as: 2s + 1d = 9.85
Now, we can solve for one of the variables by using the elimination method. We can multiply the second equation by -2 to eliminate the "s" variable:
3s + 2d = 15.75
-4s - 2d = -19.70
Adding the two equations together, we get:
-s = -3.95
Solving for "s", we find that the cost of a sandwich is $3.95. Now, we can plug this value back into one of the original equations to find the cost of a drink:
2(3.95) + 1d = 9.85
7.90 + 1d = 9.85
1d = 1.95
So the cost of a drink is $1.95. Now that we know the cost of each item, we can calculate the cost of 2 drinks and 2 sandwiches:
2(3.95) + 2(1.95) = 7.90 + 3.90 = $11.80
Therefore, Wendy and her friend would spend $11.80 on 2 drinks and 2 sandwiches at the same restaurant.
Here to learn more about the Equation at the link https://brainly.com/question/22688504
#SPJ11