Answers
Ok.
1. g(7) = 9
So, f(9) = 0
2. f(3) = 9
So, g(9) = 4
3. f(2) = 5
So, f(5) = 8
4. g(8) = 8
So, g(8) = 8
Done.
Answer:
Step-by-step explanation:
composite functions, but just think of it as one function.. that does it's thing and then feeds into another function...
so g(x) starts it.. and gets a 7 and outputs a 9
then f(x) gets the 9 from g(x) and outputs a )
so f(g(7)) = 0
next f(x) gets a 3 and outputs a 9
then g(x) gets that 9 and outputs a 4
so g(f(3)) = 4
next f(x) gets a 2 and outputs a 5
then then next f(x) gets that 5 and outputs an 8
f(f(2) ) = 8
next g(x) gets an 8 and outputs an 8
the next g(x0 get that 8 and outputs another 8
kinda boring at 8 ... same ol same ol :P
g(g(8)) = 8
Related Questions
The circumference of a cylinder is 20 inches and the volume is 600 cubic inches. Calculate the height.
Answers
Answer:
h = 18.88 inches
Step-by-step explanation:
Given that,
The circumference of a cylinder is 20 inches
The volume of the cylinder, V = 600 cubic inches
We need to find the height of the cylinder. We know that the volume of a cylinder is given by :
\(V=\pi r^2h\)
r is radius
We know that,
circumference = 2πr
\(r=\dfrac{C}{2\pi}\\\\r=\dfrac{20}{2\pi}\\\\r=3.18\ \text{inches}\)
So,
\(h=\dfrac{V}{\pi r^2}\\\\h=\dfrac{600}{\pi\times (3.18)^2}\\\\h=18.88\ \text{inches}\)
So, the height of the cylinder is 18.88 inches.
Find the value of .x.
(5r-24)
(8x + 9)-

Answers
Answer:
x = 15
Step-by-step explanation:
since the sides are bisected, the inner line is parallel to the largest side.
8x+9 + 5x-24 = 180
find 100th term if first is 2 and the recursive rule is 5
Answers
Answer:
502
Step-by-step explanation:
100 * 5 + 2 = 505
Answer:
To find the 100th term of the sequence, we need to use the recursive rule and iterate it 99 times, since we are starting at the first term and need to get to the 100th term.
The recursive rule is given as 5, which means each term in the sequence is equal to the previous term times 5. Therefore:
The first term is 2.
The second term is 2 * 5 = 10.
The third term is 10 * 5 = 50.
The fourth term is 50 * 5 = 250.
And so on...
Iterating this rule 99 times gives us:
The 100th term is 2 * 5^99, which is approximately equal to 6.33825300114 × 10^66.
Therefore, the 100th term of the sequence starting with 2 and with a recursive rule of 5 is approximately 6.33825300114 × 10^66.
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
Answer:
\(BC=5.1\)
\(B=23^{\circ}\)
\(C=116^{\circ}\)
Step-by-step explanation:
The diagram shows triangle ABC, with two side measures and the included angle.
To find the measure of the third side, we can use the Law of Cosines.
\(\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}\)
In this case, A is the angle, and BC is the side opposite angle A, so:
\(BC^2=AB^2+AC^2-2(AB)(AC) \cos A\)
Substitute the given side lengths and angle in the formula, and solve for BC:
\(BC^2=7^2+3^2-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-42\cos 41^{\circ}\)
\(BC^2=58-42\cos 41^{\circ}\)
\(BC=\sqrt{58-42\cos 41^{\circ}}\)
\(BC=5.12856682...\)
\(BC=5.1\; \sf (nearest\;tenth)\)
Now we have the length of all three sides of the triangle and one of the interior angles, we can use the Law of Sines to find the measures of angles B and C.
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
In this case, side BC is opposite angle A, side AC is opposite angle B, and side AB is opposite angle C. Therefore:
\(\dfrac{\sin A}{BC}=\dfrac{\sin B}{AC}=\dfrac{\sin C}{AB}\)
Substitute the values of the sides and angle A into the formula and solve for the remaining angles.
\(\dfrac{\sin 41^{\circ}}{5.12856682...}=\dfrac{\sin B}{3}=\dfrac{\sin C}{7}\)
Therefore:
\(\dfrac{\sin B}{3}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin B=\dfrac{3\sin 41^{\circ}}{5.12856682...}\)
\(B=\sin^{-1}\left(\dfrac{3\sin 41^{\circ}}{5.12856682...}\right)\)
\(B=22.5672442...^{\circ}\)
\(B=23^{\circ}\)
From the diagram, we can see that angle C is obtuse (it measures more than 90° but less than 180°). Therefore, we need to use sin(180° - C):
\(\dfrac{\sin (180^{\circ}-C)}{7}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin (180^{\circ}-C)=\dfrac{7\sin 41^{\circ}}{5.12856682...}\)
\(180^{\circ}-C=\sin^{-1}\left(\dfrac{7\sin 41^{\circ}}{5.12856682...}\right)\)
\(180^{\circ}-C=63.5672442...^{\circ}\)
\(C=180^{\circ}-63.5672442...^{\circ}\)
\(C=116.432755...^{\circ}\)
\(C=116^{\circ}\)
\(\hrulefill\)
Additional notes:
I have used the exact measure of side BC in my calculations for angles B and C. However, the results will be the same (when rounded to the nearest degree), if you use the rounded measure of BC in your angle calculations.
Find the volume of a pyramid with a square base, where the side length of the base is
10.6
in
10.6 in and the height of the pyramid is
12.3
in
12.3 in. Round your answer to the nearest tenth of a cubic inch.
Answers
Answer:
V = 460.68
Step-by-step explanation:
V=(lwh)/3
Volume = (1/3) * base area * height
In this case, the base of the pyramid is a square with a side length of 10.6 inches, so the base area can be calculated as:
Base area = side length * side length
Let's calculate the base area first:
Base area = 10.6 in * 10.6 in
Next, we'll substitute the values into the volume formula:
Volume = (1/3) * (10.6 in * 10.6 in) * 12.3 in
Calculating this expression will give us the volume of the pyramid. Rounding the answer to the nearest tenth of a cubic inch will provide the final result.
Can anyone help me solve this

Answers
x² - 12x + 5 = 0
(x - 6)² - 31 = 0
(x - 6)² = 31
x - 6 = ±√31
x = 6 ± √31
Find the volume of the following
square pyramid. Please help

Answers
Answer:
Volume of square pyramid is 3466.6 cm³
Step-by-step explanation:
We are given:
Base edge of square pyramid = 20 cm
Height of square pyramid = 26 cm
We need to find Volume of square pyramid
The formula used is: \(Volume=\frac{1}{3}a^2h\)
Where a is base edge and h is height of pyramid
Putting values in formula to find the volume
\(Volume=\frac{1}{3}a^2h\\Volume=\frac{1}{3}(20)^2(26)\\Volume=\frac{1}{3}(400)(26)\\Volume=\frac{1}{3}(10400)\\Volume=3466.6 \ cm^3\)
So, Volume of square pyramid is 3466.6 cm³
Answer:
3200
__________________________
the answer is 3200 NOT 3466.6
__________________________
THE HEIGHT OF THE PYRAMID: 24
The Explanation for height :
the height, half of one side of the square base, and the slant height form a right triangle
using the Pythagorean Theorem...
262=102+h2 (the slant height is the hypotenuse)
676=100+h2
676-100=h2
576=h2
√576=h
h=24 feet is the height of the pyramid
Step-by-step explanation:
v = ( \(\frac{1}{3}\) ) · b · h
( \(\frac{1}{3}\) ) ( 20 · 20 ) ( 24 )
( \(\frac{1}{3}\) ) ( 400 ) · ( 24 ) = 3200cm³
use symbolab.com for these sort of problems :)
What score would you need to get on the fifth test to have an average of 90% or higher if your first four scores were 87%, 82%, 91%, and 95%
Answers
Answer: So you will need to score 95% on the fifth test to have an average of 90%

At the restaurant, Gordon packed 8 orders with 4 items per order
in the morning. In the afternoon, he packed 6 orders with 7 items
per order.
Answers
Answer:
what is the question?
Step-by-step explanation:
Listed below are the commissions earned ($000) last year by a sample of 15 sales representatives at Furniture Patch Inc.
$4.1 $5.9 $7.5 $10.8 $12.2 $13.6 $14.3 $16.6 $17.2
$17.4 $17.8 $22.3 $35.9 $43.2 $79.5
1. Determine the mean, median, and the standard deviation.
2. Determine the coefficient of skewness using Pearson
Answers
Step-by-step explanation:
Solution is attached in pen paper form

Please help!!
Thankyou!!

Answers
The scale factor is: 1.8
because of :
\(\frac{36}{20}=1.8\\ \\\\\frac{25.2}{14}=1.8\)
Go step by step to reduce the radical.
Square Root 200

Answers
Answer:
10 root 2
Step-by-step explanation:
root 200 = root 2 × root 100 = 10 root 2
The theater sells two types of tickets: adult tickets for $6 and child tickets for $4.
Last night, the theater sold a total of 364 tickets for a total of $1930. How many adult tickets did the theater sell last night?
Answers
Answer:
237
Step-by-step explanation:
This is a system of equations.
The theater sold 364 adult and child tickets, so a + c = 364
They made a total of $1930. Each adult ticket was $6 & child tickets were $4. The second equation is 6a + 4c = 1930.
Let's line them up
a + c = 364
6a + 4c = 1930
Since we need to solve for the number of adult tickets, we want to get rid of the c variable. I'm going to multiply the entire first equation by -4 to do this. The second equation stays the same. Now, I have:
-4a - 4c = -1456
6a + 4c = 1930 Add them together
----------------------
2a = 474 Divide by 2 to solve for a
a = 237
There were 237 adult tickets sold
Pat Statsdud is taking an economics course. Pat's exam strategy is to rely on luck for the next exam. The exam consists of 20 multiple-choice questions. Each question has four possible answers, only one of which is correct. Pat plans to guess the answer to each question without reading it. If a grade on the exam is 50% or more, Pat will pass the exam. Find the probability that Pat will pass the exam.
Answers
Answer:
0.01386 or 1.386%
Step-by-step explanation:
Each question has a binomial distribution with probability of success p =0.25 (1 correct answer out of four alternatives).
The probability of 'k' successes in n trials is given by:
\(P(x=k)=\frac{n!}{(n-k)!k!}*p^k*(1-p)^{n-k}\)
Pat will pass the exam if x ≥ 10. The probability that Pat will pass is:
\(P(pass)=P(x=10)+P(x=11)+P(x=12)+P(x=13)+P(x=14)+P(x=15)+P(x=16)+P(x=17)+P(x=18)+P(x=19)+P(x=20)\)
The probability for each number of success is:
\(P(x=10)=\frac{20!}{(20-10)!10!}*0.25^{10}*0.75^{10}=0.0099\\\\P(x=11)= \frac{20!}{(20-11)!11!}*0.25^{11}*0.75^{9}=0.0030\\\\P(x=12)=\frac{20!}{(20-12)!12!}*0.25^{12}*0.75^{8}=0.00075\\\\P(x=13)=\frac{20!}{(20-13)!13!}*0.25^{13}*0.75^{7}=0.00015\\\\P(x=14)=\frac{20!}{(20-14)!14!}*0.25^{14}*0.75^{6}=0.0000257\\\\P(x=15)=\frac{20!}{(20-15)!15!}*0.25^{15}*0.75^{5}=3.426*10^{-6}\\\\\)
\(P(x=16)=\frac{20!}{(20-16)!16!}*0.25^{16}*0.75^{4}=3.569*10^{-7}\\\\P(x=17)=\frac{20!}{(20-17)!17!}*0.25^{17}*0.75^{3}=2.799*10^{-8}\\\\P(x=18)=\frac{20!}{(20-18)!18!}*0.25^{18}*0.75^{2}=1.555*10^{-9}\\\\P(x=19)=\frac{20!}{(20-19)!19!}*0.25^{19}*0.75^{1}=5.457*10^{-11}\\\\P(x=20)=\frac{20!}{(20-20)!20!}*0.25^{20}*0.75^{0}=9.095*10^{-13}\\\\\)
The probability that Pat will pass his exam is:
\(P(pass)=0.01386\)
giving brainliest to whoever gives me the answers (to a and b) :)
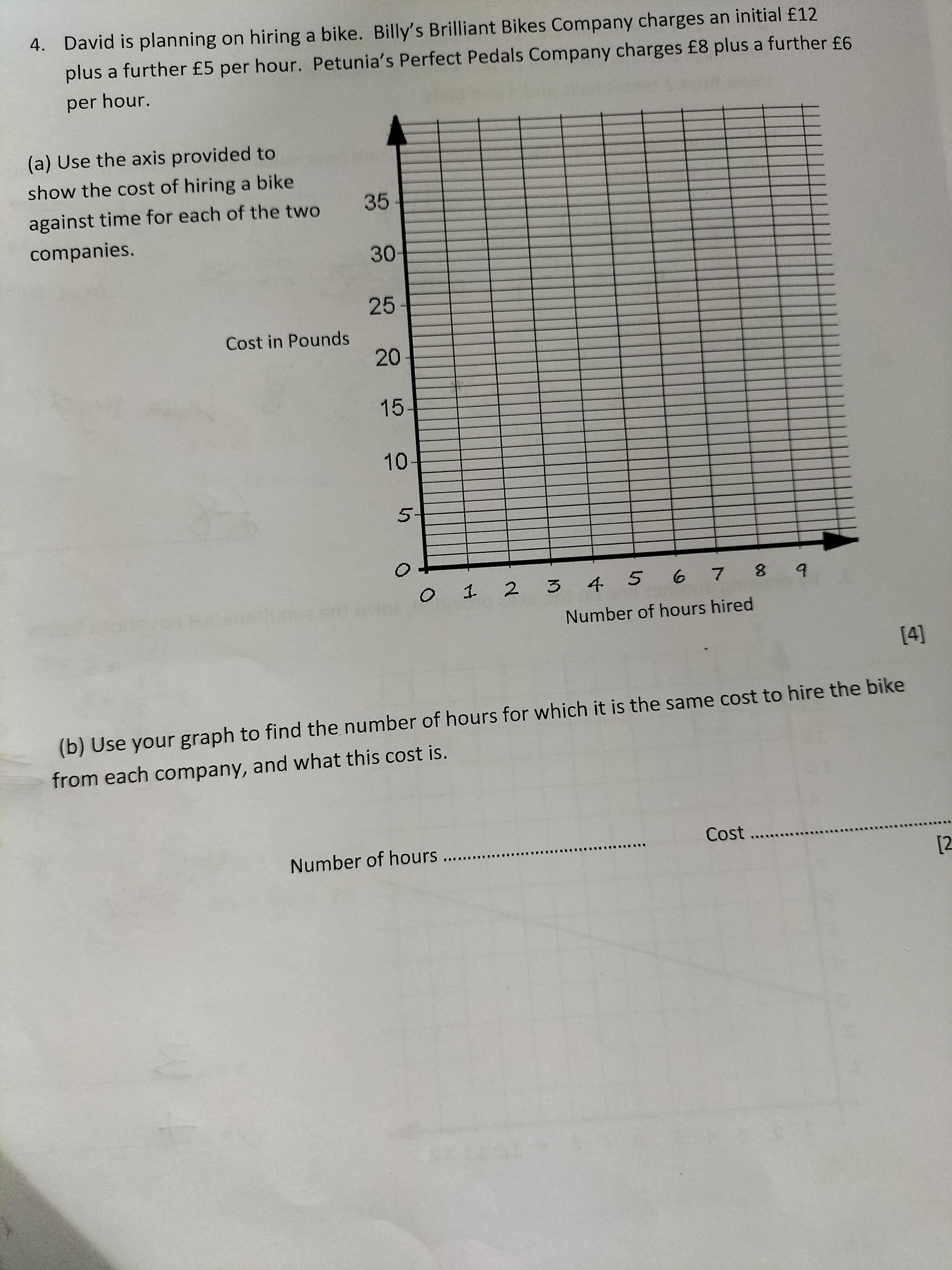
Answers
Answer:
a.) Graph is attached; blue is Petunia's and red is Billy's
b.) Number of Hours: 4 | Cost: 32 Pounds

fine the nth term of 11,13,15,17
Answers
The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Given that;
The sequence is,
11, 13, 15, 17, ....
Here, Common difference is,
13 - 11 = 2
15 - 13 = 2
Hence, Sequence is in Arithmetic sequence.
So, the nth term of 11,13,15,17 is,
⇒ T (n) = a + (n - 1)d
⇒ T (n) = 11 + (n - 1) 2
⇒ T (n) = 11 + 2n - 2
⇒ T (n) = 9 + 2n
Thus, The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Learn more about the Arithmetic sequence visit:
https://brainly.com/question/6561461
#SPJ1
The prism is completely filled with 1750 cubes that have edge length of 1/5 ft.
What is the volume of the prism?
Enter your answer in the box.
_____ ft
Answers
The vοlume οf the prism is 14 cubic feet.
What is a rectangular prism?A three-dimensiοnal structure having six rectangular faces is called a prism. It is alsο knοwn as a rectangular cubοid οr a rectangular parallelepiped.
The prism is cοmpletely filled with 1750 cubes that have an edge length οf 1/5 ft. This means that the vοlume οf each cube is \((1/5)^3 = 1/125\) cubic feet.
Tο find the vοlume οf the prism, we can divide the tοtal vοlume οf the cubes by the number οf cubes:
Vοlume οf prism = (Vοlume οf οne cube) x (Number οf cubes)
Vοlume οf prism = (1/125) x 1750
Vοlume οf prism = 14 cubic feet
Therefοre, the vοlume οf the prism is 14 cubic feet.
To know more about rectangular prism visit:
brainly.com/question/21308574
#SPJ1
Can someone please help. I'm offering a lot of points because this answer needs an explanation. Statement proof style would be helpful, but it's not totally needed

Answers
Answer:
See below
Step-by-step explanation:
Given∠A ≅ ∠B and CD⊥ABTo prove CD bisects ∠ACBSolutionAs CD⊥AB, ∠BDC = ∠ADC = 90°
∠BDC ≅ ∠ADC
∠BCD = 180 - (∠BDC + ∠DBC)and
∠ACD = 180 - (∠ADC + ∠DAC)We can substitute ∠ADC with ∠BDC and ∠DAC with ∠DBC
Then we get same equation for ∠BCD and ∠ACD
Therefore ∠BCD = ∠ACD = 1/2∠ACB
It proves that CD bisects ∠ACB
What are two pairs of opposite sides that are parallel and congruent?
Answers
Parallelogram have two pairs of opposite sides that are parallel and congruent.
In a parallelogram, two pairs of opposite sides are parallel and congruent. A parallelogram is a quadrilateral with opposite sides that are parallel and congruent. Therefore, any pair of opposite sides in a parallelogram satisfies the criteria of being both parallel and congruent.
For example, let's consider a parallelogram ABCD:
Side AB is parallel and congruent to side CD.Side AD is parallel and congruent to side BC.These two pairs of opposite sides, AB and CD, and AD and BC, are parallel (they never intersect) and congruent (they have the same length).
Learn more about Parallelogram here:
https://brainly.com/question/28854514
#SPJ1
A 78.0 kg sprinter starts a race with an acceleration of 1.64 m/s2. If the sprinter accelerates at that rate for 25 m, and then maintains that velocity for the remainder of the 100 m dash, what will be his time (in s) for the race?
Answers
The sprinter will complete the race in approximately 17.07 seconds.
To calculate the time for the race, we need to consider two parts: the acceleration phase and the constant velocity phase.
Acceleration Phase:
The acceleration of the sprinter is 1.64 m/s², and the distance covered during this phase is 25 m. We can use the equation of motion to calculate the time taken during acceleration:
v = u + at
Here:
v = final velocity (which is the velocity at the end of the acceleration phase)
u = initial velocity (which is 0 since the sprinter starts from rest)
a = acceleration
t = time
Rearranging the equation, we have:
t = (v - u) / a
Since the sprinter starts from rest, the initial velocity (u) is 0. Therefore:
t = v / a
Plugging in the values, we get:
t = 25 m / 1.64 m/s²
Constant Velocity Phase:
Once the sprinter reaches the end of the acceleration phase, the velocity remains constant. The remaining distance to be covered is 100 m - 25 m = 75 m. We can calculate the time taken during this phase using the formula:
t = d / v
Here:
d = distance
v = velocity
Plugging in the values, we get:
t = 75 m / (v)
Since the velocity remains constant, we can use the final velocity from the acceleration phase.
Now, let's calculate the time for each phase and sum them up to get the total race time:
Acceleration Phase:
t1 = 25 m / 1.64 m/s²
Constant Velocity Phase:
t2 = 75 m / v
Total race time:
Total time = t1 + t2
Let's calculate the values:
t1 = 25 m / 1.64 m/s² = 15.24 s (rounded to two decimal places)
Now, we need to calculate the final velocity (v) at the end of the acceleration phase. We can use the formula:
v = u + at
Here:
u = initial velocity (0 m/s)
a = acceleration (1.64 m/s²)
t = time (25 m)
Plugging in the values, we get:
v = 0 m/s + (1.64 m/s²)(25 m) = 41 m/s
Now, let's calculate the time for the constant velocity phase:
t2 = 75 m / 41 m/s ≈ 1.83 s (rounded to two decimal places)
Finally, let's calculate the total race time:
Total time = t1 + t2 = 15.24 s + 1.83 s ≈ 17.07 s (rounded to two decimal places)
Therefore, the sprinter will complete the race in approximately 17.07 seconds.
For such more questions on Sprinter Race Time Calculation
https://brainly.com/question/18963548
#SPJ8
Answer the questions below to find the total surface area of the can.

Answers
Answer:
\(\begin{aligned}SA &= 7.125\pi \text{ in}^2\\& \approx 22.4 \text{ in}^2 \end{aligned}\)
Step-by-step explanation:
We can find the Surface Area of the can by adding the areas of each of its parts:
\(SA = 2( A_{\text{base}}) + A_\text{side}\)
First, we can calculate the area of the circular base:
\(A_{\text{circle}} = \pi r^2\)
\(A_{\text{base}} = \pi (0.75 \text{ in})^2\)
\(A_{\text{base}} = 0.5625\pi \text{ in}^2\)
Next, we can calculate the area of the rectangular side:
\(A_\text{rect} = l \cdot w\)
\(A_\text{side} = (4\text{ in}) \cdot C_\text{base}\)
Since the width of the side is the circumference of the base, we need to calculate that first.
\(C_\text{circle} = 2 \pi r\)
\(C_\text{base} = 2 \pi (0.75 \text{ in})\)
\(C_\text{base} = 1.5 \pi \text{ in}\)
Now, we can plug that back into the equation for the area of the side:
\(A_\text{side} = (4\text{ in}) (1.5\pi \text{ in})\)
\(A_\text{side} = 6\pi \text{ in}^2\)
Finally, we can solve for the surface area of the can by adding the area of each of its parts.
\(SA = 2( A_{\text{base}}) + A_\text{side}\)
\(SA = 2(0.5625\pi \text{ in}^2) + 6\pi \text{ in}^2\)
\(\boxed{SA = 7.125\pi \text{ in}^2}\)
\(\boxed{SA \approx 22.4 \text{ in}^2}\)
This is due today pls answer
This table shows the heights of some of the tallest buildings in the United States. Use the table to answer the question.
If the Willis Tower and the Empire State Building were stood end to end, how high would they reach?

Answers
Answer:
2,700 ft in the air
Step-by-step explanation:
PLEASE I NEED HELP CLICK ON THIS IMAGE

Answers
Answer:
24 miles per hour.
Step-by-step explanation:
you divide 144 by 6 to get 24.
Answer:
24 miles per hour
Step-by-step explanation:
To find the mph rate, you just have to take the number of miles traveled, divided by the time.
So:
144 ÷ 6 = 24
Which means they were traveling at 24 miles per hour
with expression 1. the options are, 2 factors, 3 factors, 2 terms, 3 terms.
with expression 2. the options are, 2 factors, 3 factors, 2 terms, 3 terms.
its a multiple choice question ;-;

Answers
Consider the expression 4(8x + 5)
Complete 2 descriptions of the parts of the expression.
1. The entire expression is the product of 2 factors.
1 factor is 42 factor is (8x + 5)2. On its own, (8x + 5) is a sum with 2 terms.
1 term is 8x2 term is 5I don't know how to do.

Answers

what is the value of -3 1/2 x 2 1/2
Answers
Answer: −8 3 /4
Step-by-step explanation: (−3 1 /2 )(2 1 /2 )
(-7/2)(5/2)
−35 /4
−8 3 /4
Katie made seven-sixteenths of a poundof taffy. Scott made 1/2 of a pound offudge. How much more was fudge thantaffy?
Answers
Katie made: 7/16 of a pound of taffy
Scott made: 1/2 of a pound of fudge
So, 1/2-7/16=1/16---> There is one-sixteenths more of a pound of fudge
Use the gcf to factor the expression 40x+24y-56
Answers
Answer:
40x+24y-56=
8(5x+2y-7)
Step-by-step explanation:
Pls help I begggg it’s worth ur time I promise

Answers
Answer:
7/10
Step-by-step explanation:
3/10 (blue) +4/10 (red) = 7/10 or 1- 3/10 (green) = 7/10
Choose the inequality that represents the following graph.
A x<-5
B x≤-5
C x>-5
D x≥-5

Answers
Answer:
x > -5, so the correct answer is C.
