Write the equation of a quadratic function with roots at 2 and -2,
and a vertex at (0, 2). Write the equation in standard form.
Answers
The standard form of the equation is y = -x²/2 + 2
What is the standard form of the equation?
In an equation's standard form, 0 is often on the right side, with the remaining expressions on the left. Additionally, the terms are organized according to decreasing exponents. Simply use arithmetic operations on both sides to make the right side of an equation equal to zero to put it in standard form.
Here, we have
Given roots 2 and -2,
and a vertex at (0, 2).
The equation of a given vertex may be written as
y = a(x−0)² + 2 for some constant a
Now, we put
x = 2, y = 0 into this equation, we find:
0 = a(2−0)²+ 2
= 4a + 2
a = −1/2
So in vertex form, the equation is:
y = (-1/2)(x−0)² + 2
In standard form :
y = -x²/2 + 2
Hence, the standard form of the equation is y = -x²/2 + 2
to learn more about the standard form of the equation from the given link
https://brainly.com/question/19169731
#SPJ1
Related Questions
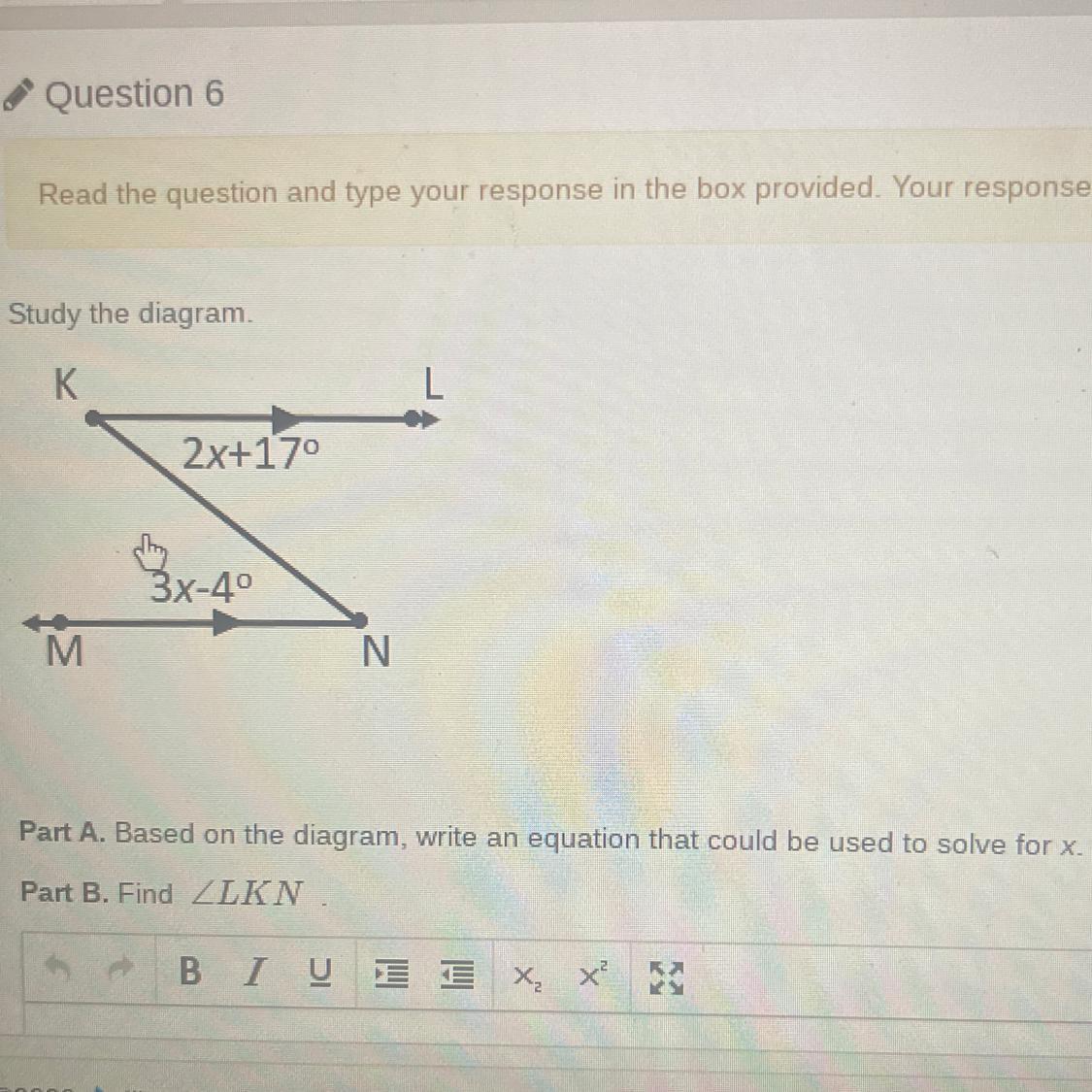
Study the diagram.
K
M
2x+17⁰
3x-4°
N
Part A. Based on the diagram, write an equation that could be used to solve for x.
Part B. Find LKN
Answers
Answer:
A. 2x +17° = 3x -4°
B. x = 21°; ∠LKN = 59°
Step-by-step explanation:
Given alternate interior angles of 2x +17° and 3x -4°, you want an equation for x, and the measure of these angles.
A. EquationThe marked angles are alternate interior angles at transversal KN with respect to parallel lines KL and MN. That means they are congruent. An equation showing they have the same measure can be used to solve for x.
2x +17° = 3x -4°
B. AngleAdding 4° -2x to both sides of the equation gives ...
21° = x
Using this value in the expression for ∠LKN, we have ...
∠LKN = 2(21°) +17° = 42° +17°
∠LKN = 59°
Actual demand for the past 16 periods is shown below. Prepare a trend adjusted exponential smoothing forecast using the following parameters: a = 4, B = .3, TAF5 = 652.67, and T5 = -33. (Round all you
Answers
To forecast future demand using trend adjusted exponential smoothing, the given information includes actual demand for the past 16 periods and the parameters required for the forecast. The parameters include the smoothing constant (α), the trend smoothing constant (β), the trend-adjusted forecast for period 5 (TAF5), and the trend for period 5 (T5).
The question asks to prepare a trend-adjusted exponential smoothing forecast based on these parameters.
Trend adjusted exponential smoothing combines exponential smoothing with a trend component to forecast future values. The formula for calculating the forecast is:
Ft+1 = Ft + Tt + α * (At - Ft) + β * (Tt - Tt-1)
Where:
Ft is the forecast for period t
Tt is the trend component for period t
At is the actual demand for period t
α is the smoothing constant
β is the trend smoothing constant
To start, we need to initialize the forecast and trend values. In this case, we are given the trend-adjusted forecast for period 5 (TAF5) and the trend for period 5 (T5). So, we set F5 = TAF5 and T5 = T5.
Next, we can use the formula to calculate the forecast and trend values for the remaining periods.
We iterate through the periods from t = 6 to t = 16, applying the formula to update the forecast and trend values based on the actual demand for each period.
Finally, we round the forecast values to the desired precision.
By following this procedure and applying the given parameters, we can prepare a trend-adjusted exponential smoothing forecast for the future demand.
The forecast values will reflect the trend in the historical data while incorporating the smoothing constants for better accuracy.
To learn more about accuracy visit:
brainly.com/question/28073948
#SPJ11
Si la hipotenusa de un triángulo rectángulo mide 2 cm y uno de sus lados mide 1 cm ¿ cuánto mide el otro lado ?
Answers
Answer:
Step-by-step explanation:
a^2+b^2=c^2
c^2-b^2=a^2
2^2-1^2=c^2
c^2=3
c=\(\sqrt{3}\)
espero que esto te ayude, pero no se si esta correcto lo siento
1) "teacher" wants to build a rectangular dog bowl stand. The top of it will have a perimeter 55 1/2 inches. The length is twice as long as the width. What are the dimensions (length and width) of the top of the dog bowl stand? (Note: Your answer should be in fraction form, not a decimal.) 2) During their basketball game, "teacher 1" shoots twice as many airballs as "teacher 2". "teacher 3" shoots 4 airballs less than "teacher 2". If they shot 24 airballs together, how many airballs did each teacher shoot?
Answers
Answer:
1)
\(L=18 \frac{1}{2} in\)
\( W= 9 \frac{1}{4} in\)
2)
\(T_{1}=14 balls\)
\(T_{2}=7 balls\)
\(T_{3}=3 balls\)
Step-by-step explanation:
In order to solve this problem, we need to build the equations we need. Since there are two values we want to figure out (length and width) we will then need two equations to solve simultaneously.
First, the problem tells us that the perimeter is 55 1/2 in, which can be rewritten as an improper fraction:
\(55 \frac{1}{2}= \frac{55*2+1}{2}= \frac{111}{2}\)
Next, we also know the perimeter of a rectangle is found by using the following formula:
P=2L+2W
where L is the length of the rectangle and W is its width.
So our first equation will look like this:
\(2L+2W=\frac{111}{2}\)
Next, the problem tells us that the width of the rectangle is twice its width, so our second equation will look like this:
L=2W
which can be substituted into our first equation:
\(2L+L=\frac{111}{2}\)
Now, we can solve this for L, so we get:
\(3L=\frac{111}{2}\)
\(L=\frac{111}{2*3}\)
\(L=\frac{111}{6}=18 \frac{3}{6}=18 \frac{1}{2}\)
so we can now use this information to find its width:
L=2W
\( \frac{111}{6}=2W\)
so
\(W=\frac{111}{6*2}\)
\(W=\frac{111}{12}=9\frac{3}{12}=9\frac{1}{4}\)
2)
When solving this problem it is a good idea to split it into little chunks of information. The first sentence says:
"... "teacher 1" shoots twice as many airballs as "teacher 2"."
This can be translated as an equation like this:
\(T_{1}=2T_{2}\)
The next sentence says:
""teacher 3" shoots 4 airballs less than "teacher 2"."
This can be written as an equation like this:
\(T_{3}=T_{2}-4\)
and finally, the problem states: "... they shot 24 airballs together,..."
This can be written as an equation like this:
\(T_{1}+T_{2}+T_{3}=24\)
so now we can do substitutions. We can take the first and second equations and write them into the third equation so we get:
\(2T_{2}+T_{2}+T_{2}-4=24\)
so now we can solve this equation for \(T_{2}\), so we get:
\(2T_{2}+T_{2}+T_{2}=24+4\)
\(4T_{2}=28\)
\(T_{2}=\frac{28}{4}\)
\(T_{2}=7\)
and once we got this answer, we can find the remaining two answers:
\(T_{1}=2T_{2}\)
\(T_{1}=2(7)\)
\(T_{1}=14\)
and
\(T_{3}=T_{2}-4\)
so we get:
\(T_{3}=7-4\)
\(T_{3}=3\)
Answer:
1)
Step-by-step explanation:
1)
If someone has a cylindrical container filled to the top with water and pours the water in a cone with the same diameter, d= 6in, and height, h=14 in, into the cone, what is the volume of water left in the cylinder?
Answers
Answer:
6.2
Step-by-step explanation: TOOK THE TEST
find the value of x!

Answers
Answer:
\(x=77\)
Step-by-step explanation:
103 -x + 2x = 180
Help help help
Help help

Answers
Answer:
x = 2, y = 4
Step-by-step explanation:
x + \(\frac{3}{4}\) y = 5 ( multiply through by 4 to clear the fraction )
4x + 3y = 20 → (1)
x - \(\frac{1}{2}\) y = 0 ( multiply through by 2 to clear the fraction )
2x - y = 0 → (2)
Multiplying (2) by 3 and adding to (1) will eliminate y
6x - 3y = 0 → (3)
Add (1) and (3) term by term to eliminate y
10x + 0 = 20
10x = 20 ( divide both sides by 10 )
x = 2
Substitute x = 2 into either of the 2 equations and solve for y
Substituting into (1)
4(2) + 3y = 20
8 + 3y = 20 ( subtract 8 from both sides )
3y = 12 ( divide both sides by 3 )
y = 4
Solution is x = 2, y = 4
the following declaration statement is constructed incorrectly. correct the statement.int[] hours = 8, 12, 16;
Answers
The corrected statement should look like this:
```java
int[] hours = {8, 12, 16};
```
It looks like you are trying to create an integer array in Java called "hours" and initialize it with the values 8, 12, and 16. The given statement has incorrect syntax.
Declare the integer array using "int[]" followed by the variable name "hours".
This tells the Java compiler that you want to create an array of integers called "hours".
Use the assignment operator "=" to assign values to the array.
Enclose the values you want to assign to the array within curly braces "{" and "}" and separate each value with a comma.
The corrected statement should look like this:
```java
int[] hours = {8, 12, 16};
```
Now, the "hours" integer array is initialized correctly with the given values.
The syntax for declaring and initializing an integer array in Java is:
```java
data Type[] array
Name = {value1, value2, value3, ...};
```
In this case, "data Type" is "int", "array
Name" is "hours", and the values are 8, 12, and 16.
Remember to keep your code clean and concise to avoid syntax errors and make it easier for others to understand.
For similar question on statement.
https://brainly.com/question/26134656
#SPJ11
A 2-quart carton of yogurt costs $3.68. What is the price per cup?
Answers
Answer:
46 cents
Step-by-step explanation:
2 quarts has 8 cups and 3.68 ÷ 8 = 0.46
let a = [1 1 1 0]. assume fo = 0. prove by mathematical induction
Answers
We have proven that \(a^k\) = [1 1 1 ... 1 0] for any positive integer k.
What do you mean by mathematical induction?The art of demonstrating a claim, theorem, or formula that is regarded as true for each and every natural number n is known as proof. There are numerous generalized assertions in mathematics that take the form of n.
To prove a statement using mathematical induction, we need to show that it holds for a base case and then demonstrate that if it holds for a specific value, it also holds for the next value. Let's proceed with the proof:
Base Case:
For n = 1, we have:
\(a^1\) = [1]
Since the only element in \(a^1\) is 1, which is equal to fo, the statement holds for the base case.
Inductive Step:
Assume that the statement holds for some positive integer k, i.e., assume that \(a^k\) = [1 1 1 ... 1 0] with k elements, where the last element is 0.
We want to prove that the statement also holds for k + 1, i.e., we need to show that \(a^{(k+1)\) = [1 1 1 ... 1 0] with (k+1) elements, where the last element is 0.
Using the assumption, we have:
\(a^{(k+1)\) = \(a^k\) * a
Multiplying \(a^k\) by a, we get:
\(a^{(k+1)\) = [1 1 1 ... 1 0] * [1 1 1 0]
To obtain the product, we perform element-wise multiplication:
\(a^{(k+1)\) = [1*1 1*1 1*1 ... 1*1 0*0]
= [1 1 1 ... 1 0]
Since the last element of \(a^k\) is 0, multiplying it by any value will still result in 0. Therefore, the last element of \(a^{(k+1)\) is 0.
Thus, the statement holds for k + 1.
By the principle of mathematical induction, the statement is proven to hold for all positive integers.
Therefore, we have proven that \(a^k\) = [1 1 1 ... 1 0] for any positive integer k.
Learn more about mathematical induction on:
https://brainly.com/question/29503103
#SPJ4
10. In a library, Jolly deaned and arranged 4599 books on the shelf. Gopal arranged 1945 less books than Jolly. How many books were arranged in all by Gopal?
Answers
Answer: 2654
Step-by-step explanation:
you take jolly's number 4599 and subtract Gopal's number of 1945
Solve this for me please.

Answers
Answer:
3. 8 feet
Step-by-step explanation:
To find the horizontal distance (x) in feet, we can use the following steps:
Step 1: Determine the vertical height that the box has been lifted.
The difference between the two points is:
9 ft - 3 ft = 6 ft.
Therefore, the box has been lifted 6 feet.
Step 2: Use the slope of the ramp to find the horizontal distance (x).
The slope of the ramp is given as 3/4. This means that for every 3 feet the ramp rises vertically, it moves 4 feet horizontally. We can set up a proportion to solve for x:
3/4 = 6/x
We can cross-multiply to get:
3x = 24
Dividing both sides by 3 gives us:
x = 8
Therefore, the horizontal distance (x) is 8 feet.
Given triangle ABC is congruent to DEC find m

Answers
First, we know that angle B is congruent to angle E.
2x + 40 = 5x + 10
2x + 30 = 5x
30 = 3x
x = 10
Angle B and Angle E = 60 degrees
Angle C = 14 degrees
Remember that the interior angles of a triangle always add up to 180 degrees. Now that we know 2 of the 3 angles of these triangles, and because they are congruent, all that's left to do is find Angle A/D by setting up a simple equation.
60 + 14 + D = 180
74 + D = 180
D = 106
Angle D = 106 degrees
Hope this helps!
Answer:
Step-by-step explanation:
<E = <A property of congruency.
<A = 5x + 10 Comes from the fact that <A and <E are equal.
Three angles of the triangle are given. They add to 180 degrees.
2x + 40 + x + 4 + 5x + 10 = 180 Combine like terms
8x + 54 = 180 Subtract 54 from both sides.
8x + 54 - 54 = 180 - 54 Combine
8x = 126 Divide by 8
8x/8 = 126/8
x = 15.75
<B = <D Congruency and parallel lines
<D = 2x + 40 Substitute for x
<D = 2*15.75 + 40 Combine
<D = 31.5 + 40
<D = 71.5
If you deposit $1,000 today at the bank at 7% compounded semi-annually, how much will you get in next 15 years? (Calculator & Spreadsheet
Answers
If you deposit $1,000 today at a bank with a 7% interest rate compounded semi-annually, you will have approximately $3,439.96 in 15 years.
To calculate this, we can use the formula for compound interest with semi-annual compounding: A = P * (1 + r/n)^(n*t), where A is the future amount, P is the principal amount, r is the interest rate, n is the number of compounding periods per year, and t is the number of years.
Plugging in the values, we have A = $1,000 * (1 + 0.07/2)^(2*15). Evaluating this equation, we find that the future amount is approximately $3,439.96. Therefore, after 15 years, your initial deposit of $1,000 will have grown to around $3,439.96.
The semi-annual compounding means that the interest is applied twice a year, allowing your savings to grow at a faster rate compared to annual compounding. This results in a higher final amount over time. It's important to note that this calculation assumes no additional deposits or withdrawals are made during the 15-year period.
Learn more about numbers here: brainly.com/question/13045235
#SPJ11
Tom buys a condominium for $42,600. he makes a down payment of 15%, and pays these closing costs: survey $225; inspection, $110; mortgage fee, $852; legal fees, $450; title insurance, $286. what is the amount of the down payment? what are the total closing costs? how much will he need to bring to the closing (down payment + closing costs)?
Answers
Tom will need to bring to the closing $54,341.27 He would need 12 and it would cost 50k.
What is the meaning of down payment?The meaning down payment is a part of the full price paid at the time of purchase or delivery with the balance to be paid later.
We have given that,
Tom buys a condominium for $42,600.
Inspection, $110; mortgage fee, $852; legal fees, $450; title insurance, $286
He makes a down payment of 15% and pays these closing costs to survey $225.
9% payments: $563.24
7% payments: $494.75.
Monthly savings: $69.49
9% total repaid: $2022,764.90
7% total repaid: $148,423.63
Savings: $54,341.27
To learn more about the savings visit:
brainly.com/question/25787382
#SPJ1
Consider ABC.
What is the length of AC
A. 32units
B.48units
C.16units
D.24units

Answers
Segment GH is known as a mid segment, which is parallel and 1/2 of the segment parallel to it, in this case AC. :)
How many ways can 8 people be assigned to 2 triple and 2 double rooms
Answers
Answer:
66 ways in the triple rooms, 28 ways in the double rooms
Step-by-step explanation:
In total: 8 people;
There are 2 triple rooms, so 3 people can live in one triple room:
In the first triple room:
8×7×6 = 336 / 3×2×1 = 56 ways (we have to divide the number of ways by the factorial, because the order of people doesn't matter)
In the second triple room:
5×4×3 = 60 / 3×2×1 = 10 ways (since we can't choose the same people from the first triple room)
In total: 56+10 = 66 ways
Now, double rooms:
Ir the first double room:
8×7 = 56 / 2×1 = 28 ways
In the second double room:
6×5 = 30 / 2×1 = 15 ways
In total: 28+15 = 43 ways
I don't know if I got this right, though...
2. Latrina is planning to serve hors d'oeuvres at her wedding. She plans on offering
8 hors d'oeuvres for every 3 people. If she has 240 people RSVP to the wedding, how many hors
d'oeuvres will she serve? Set up a proportion to solve.
I KNOW:
PLAN AND WORK:
I NEED TO KNOW:
SOLUTION:
Answers
She will serve 640 hors d'oeuvres to 240 people.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
Total number of people = 240
Number of hors d'oeuvres per 3 people = 8
Number of hors d'oeuvres to serve 240 people.
= 8 x 240 ÷ 3
= 8 x 240/3
= 8 x 80
= 640
Thus,
The number of hors d'oeuvres to serve is 640
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Can somebody please help me because I don’t understand

Answers
Answer: x = 64
Step-by-step explanation:
5/8x = 40
We divided by 5/8 from both sides
40/1 divided by 5/8 is the same as
40/1 times 8/5 = 320/ 5 = 64
x= 64
The sum of two numbers is 38. The greater number is 8 more than the other number. Find each number. Use a system of linear equations to justify your answer.
Answers
Answer:
x = 23 and y = 15
Let one number be x and another be y
The sum of two numbers is 38
x + y = 38
x = 38 - y
The greater number is 8 more than the other number.
x - y = 8
x = 8 + y
solve both equations:
8 + y = 38 - y
y + y = 38 - 8
2y = 30
y = 15
solve for x:
x = 8 + y
x = 8 + 15
x = 23
Let one number be x and another be y
The sum of two numbers is 38
x + y = 38
x = 38 - y
The greater number is 8 more than the other number.
x - y = 8
x = 8 + y
solve both equations:
8 + y = 38 - y
y + y = 38 - 8
2y = 30
\({{\bold{{{{{ \green{y = 15}}}}}}}}\)
solve for x:
x = 8 + y
x = 8 + 15
\({{\bold{{{{{ \green{x = 23}}}}}}}}\)
\({{\bold{{{{{ \red{so, x \: = 23 \: and \: y \: = 15}}}}}}}}\)
the president of a university claimed that the entering class this year appeared to be larger than the entering class from previous years but their mean sat score is lower than previous years. he took a sample of 30 of this year's entering students and found that their mean sat score is 1,501 with a standard deviation of 53. the university's record indicates that the mean sat score for entering students from previous years is $1,520. he wants to find out if his claim is supported by the evidence at a 5% significance level. which of the following best describes a type i error? the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed not lower the president concludes that the mean sat score of the entering students is higher than previous years when it is indeed higher the president concludes that the mean sat score of the entering students is not lower than previous years when it is indeed lower the president concludes that the mean sat score of the entering students is lower than previous years when it is indeed lower
Answers
The result is not statistically significant.
To test the hypothesis is the mean SAT score is less than 1520 at 5% significance level.
The null hypothesis is
H₀ : μ ≥ 1520
The alternative hypothesis is
Hₐ : μ ≤ 1520
then the test statistic is,
t = (x - μ)/(s/√n)
= (1501 - 1520)/(53/√20)
t = - 1.603
The t-test statistic is - 1.603.
Degree of freedom n - 1 = 20 - 1 = 19
Hence the t-critical value is -1.792.
The conclusion is that the t value corresponds to sample statistics is not fall in the critical region, so the null hypothesis is not rejected at 5% level of significance. There is insignificance evidence indicates that the mean SAT score is less than 1520.
The result is not statistically significant.
To know more about mean score here
https://brainly.com/question/16907497
#SPJ4
Which expression has a value of 1?
Answers
Answer:
x/x=1
Step-by-step explanation:
is the answer to your problem :)
solve general solutions
\( \sqrt{3tan \:} (2x - 10) + 1 = 0\)
Answers
\(\\ \rm\Rrightarrow \sqrt{3tan(2x-10)}+1=0\)
\(\\ \rm\Rrightarrow \sqrt{3tan(2x-10)}=-1\)
\(\\ \rm\Rrightarrow 3tan(2x+10)=1\)
\(\\ \rm\Rrightarrow tan(2x+10)=1/3\)
1/3=0.33..tan^{-1}(0.33)≈18\(\\ \rm\Rrightarrow 2x+10=18\)
\(\\ \rm\Rrightarrow 2x=8\)
\(\\ \rm\Rrightarrow x=4\)
If DE bisects <ABC.find the value of x if m<ABC=7x+29 and m<DBC=99°
Answers
Answer:
19
Step-by-step explanation:
If DE bisects <ABC, this means that <ABE = <EBC
Also <DBC+<EBC = 180
99+<EBC = 180
<EBC = 180-99
<EBC = 81
Also <ABC =<ABE+<EBC
<ABC =<EBC+<EBC
7x+29 = 81+81
7x = 162-29
7x = 133
x = 133/7
x = 19°
Hence the value of x is 19°
Find the solution of the differential equation that satisfies the given initial condition. 5. (ex + y)dx + (2 + x + yey)dy = 0, y(0) = 1 6. (x + y)2dx + (2xy + x2 – 1)dy = 0, y(1) = 1
Answers
5. The solution to the differential equation (ex + y)dx + (2 + x + yey)dy = 0 with y(0) = 1 is y = 2e^(-x) – x – 1. 6. The solution to the differential equation (x + y)²dx + (2xy + x² – 1)dy = 0 with y(1) = 1 is y = x – 1.
5. To solve the differential equation (ex + y)dx + (2 + x + yey)dy = 0 with the initial condition y(0) = 1, we can use the method of exact differential equations. By identifying the integrating factor as e^(∫dy/(2+yey)), we can rewrite the equation as an exact differential. Solving the resulting equation yields the solution y = 2e^(-x) – x – 1.
To solve the differential equation (x + y)²dx + (2xy + x² – 1)dy = 0 with the initial condition y(1) = 1, we can use the method of separable variables. Rearranging the equation and integrating both sides with respect to x and y, we obtain the solution y = x – 1.
These solutions satisfy their respective initial conditions and represent the family of curves that satisfy the given differential equations.
Learn more about Separable variables here: brainly.com/question/30417970
#SPJ11
SOMEONE HELP I NEED A ANSWER ASAP
If x = 5 and y = 6, what is 2x - 12/y?
Answers
2(5)-12/6
10-2=8
For the holidays, Antonio is driving to visit his grandparents who live 441 miles away. Antonio's car gets 31.5 miles per gallon of gas when he is driving on the highway. In order to budget for his trip, Antonio wants to know how much gas he will need.
Use an equation to find how much gas Antonio needs for the drive.
Antonio needs
gallons of gas.
Answers
Answer:
12
Step-by-step explanation:
The final exam had three times as many points as the first test, plus a bonus question worth 25 points . The final exam was worth 160 points (including the bonus). How many points was the first test worth?
Answers
Answer:
45
Step-by-step explanation:
The final had an extra credit as 25, so without it it would be 135. Then, you would divide by three to find that the first test had 45 points.
Answer:
45
Step-by-step explanation:
The final had an extra credit as 25, so without it it would be 135. Then, you would divide by three to find that the first test had 45 points.
What’s the answer to this

Answers
Answer:
Step-by-step explanation:
Use angle bisector theorem
(3x-3)/5x = 24/44
Solve:
x= 6
GEOMETRY
Help me my teacher doesn’t do their job right
