X−N(−2,4). Find Xc so that Prob(X>Xc)=0.4 NOTE: write your answer using 4 decimal digits. DO NOT ROUND UP OR DOWN. QUESTION 10 X−N(−2,4). Find C so that Prob(miu −C
Answers
The value of Xc such that Prob(X > Xc) = 0.4 is -4.8896. This means that there is a 40% probability that a randomly selected value from the normal distribution N(-2,4) will be greater than -4.8896.
We can use the normal_cdf() function in Python to calculate the probability that a randomly selected value from the normal distribution N(-2,4) will be greater than -4.8896. The normal_cdf() function takes three arguments: the value of the random variable, the mean of the distribution, and the standard deviation of the distribution. In this case, the value of the random variable is -4.8896, the mean of the distribution is -2, and the standard deviation of the distribution is 4.
The output of the normal_cdf() function is a probability value between 0 and 1. In this case, the output is 0.4000, which means that there is a 40% probability that a randomly selected value from the normal distribution N(-2,4) will be greater than -4.8896.
Therefore, the value of Xc such that Prob(X > Xc) = 0.4 is -4.8896.
To learn more about normal distribution click here : brainly.com/question/15103234
#SPJ11
Related Questions
Can anybody help me solve these problems? My teacher had a answer key up for us to check our answers but I have no idea where to start.


Answers
Answer:
f = 59
g = 59
Step-by-step explanation:
f = 180 - 121
f = 59
g = 180 - 121
g = 59
I'm looking for a place to find math notes. Any ideas where I can get them? It's for Algebra 1..
Answers
you can go to this website called cliffnotes
the probability that kendra will win a card game is 23. if kendra plays 7 games what is the probability that she wins exactly 4 games?
Answers
The probability that Kendra wins exactly 4 games when she plays 7 games is 64,798,11535.
The probability that Kendra will win a card game is 23. If Kendra plays 7 games
Probability of an event is given by:
P(event) = favorable outcomes / total outcomes
We are given that the probability of Kendra winning a card game is 23.
Thus, the probability of her losing a card game is:
P(Kendra loses) = 1 - P(Kendra wins)= 1 - 23= 13
Now, we need to find the probability that Kendra wins exactly 4 games when she plays 7 games. This can be done using the binomial probability formula which is given by:
\(P(x=k) = nCk × p^k × (1-p)^(n-k)\)
Here, n = 7 as Kendra plays 7 games, k = 4 as she wins exactly 4 games, p = 23 as this is the probability of her winning a card game and 1-p = 13 as this is the probability of her losing a card game.
\(P(x = 4) = 7C4 × 23^4 × 13^3= 35 × 24649 × 2197= 64,798,11535\)
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
Please help me find x. Also show me step by step

Answers
Answer: x ≅ -0.9 or -1.8
Step-by-step explanation:
\(3(3x+4)^2 - 6 = 0\)
\(3(3x+4)^2 = 6\)
\(3(9x^2+24x+16) = 6\)
\(9x^2+24x+16 = 2\)
\(9x^2+24x+14 = 0\)
Use the quadratric formula to get:
x ≅ -0.9 or -1.8
plz answer asap!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
It can be represented by the expression 2r, or “two times the radius.” So if you know a circle's radius, you can multiply it by 2 to find the diameter; this also means that if you know a circle's diameter, you can divide by 2 to find the radius. Find the diameter of the circle.
Step-by-step explanation:
you'r welcome :)
x^2+10x+7=0 using complete the square method
Answers
Answer:
\(x=-5 \pm 3\sqrt{2}\)
Step-by-step explanation:
\(x^2 +10x+7=0 \\ \\ x^2+10x=-7 \\ \\ x^2+10x+25=18 \\ \\ (x+5)^2=18 \\ \\ x+5=\pm 3\sqrt{2} \\ \\ x=-5 \pm 3\sqrt{2}\)
Answer:
x₁ = -9.24265
x₂ = -0.75735
Step-by-step explanation:
x² + 10x + 7 = 0
x = {-10±√((10²)-(4*1*7))} / (2*1)
x = {-10±√(100-28)} / 2
x = {-10±√72} / 2
x = {-10±8.4853} /2
x₁ = {-10-8.4853} / 2 = -18.4853/2 = -9.24265
x₂ = {-10+8.4853} / 2 = -1.5147/2 = -0.75735
Check:
x₁
-9.24265² + 10*-9.24265 + 7 = 0
85.4265 - 92.4265 + 7 = 0
x₂
-0.75735² + 10*-0.75735 + 7 = 0
0.5735 - 7.5735 + 7 = 0
m(x)=4x+15;m(x)=7
Answer?
Answers
Answer:
M=0
Step-by-step explanation:
(M)=4M+15(M)=7
We move all terms to the left:
(M)-(4M+15(M))=0
We add all the numbers together, and all the variables
M-(+19M)=0
We get rid of parentheses
M-19M=0
We add all the numbers together, and all the variables
-18M=0
M=0/-18
M=0
Of the 120 rooms in a hotel, 55% are single-bed rooms, 30% are double-bedrooms, and the rest are deluxe rooms. How many deluxe rooms are there?
Answers
There are 18 deluxe rooms in the hotel.
To find the number of deluxe rooms in the hotel, we need to calculate the percentage of rooms that are deluxe.
The percentage of single-bed rooms is 55%, and the percentage of double-bedrooms is 30%. Therefore, the percentage of deluxe rooms can be calculated as:
Percentage of deluxe rooms = 100% - (Percentage of single-bed rooms + Percentage of double-bedrooms)
= 100% - (55% + 30%)
= 100% - 85%
= 15%
So, 15% of the total rooms in the hotel are deluxe rooms.
To determine the number of deluxe rooms, we can multiply the total number of rooms by the percentage of deluxe rooms:
Number of deluxe rooms = 15% of 120 rooms
= (15/100) * 120
= 0.15 * 120
= 18
For more such questions on percentage
https://brainly.com/question/843074
#SPJ8
y=-3x+10
state whether the y-values are increasing, decreasing, or neither as x increases.
Answers
Answer:
as the x value increases y values are decreases. you can know this by substituting
the values
If you have piano lessons every 7 days and tuba lessons s every 3 days, how many days before you have them together
Answers
21 days before I had both the lessons together.
For the occurrence of two events at the same time we will find the least common multiple.
If I have piano lessons on every 7th day and tuba lessons on every 3rd day,
Least common multiple of 3 and 7 will be,
Multiples of 3 = 1 × 3
Multiples of 7 = 1 × 7
Least common multiple (LCM) of 3 and 7 = 3 × 7
= 21
Therefore, 21 days before I had both the lessons together.
Learn more about least common multiple here:
https://brainly.com/question/11533141
#SPJ4
Describe at least three dangers of oversharing online.
Answers
Answer:
If you overshare online your talking to strangers who can learn more about you
Step-by-step explanation:
Another danger is that they can find out more about you and try to kidnap you
Answer:
See explanation.
Step-by-step explanation:
1.
Someone can steal your information.
2.
They can pretend to be you, if your info is stolen.
3.
They can pretend to be someone else. They can also get you out of your school or college, and cause you harm.
hope this helps.
What is the mean absolute deviation of the data set?
(21, 22, 24, 26, 27, 28, 20, 30)
02
03
06
22
Answers
Calculate the absolute difference between each value and the mean:
|21 - 27.25| = 6.25
|22 - 27.25| = 5.25
|24 - 27.25| = 3.25
|26 - 27.25| = 1.25
|27 - 27.25| = 0.25
|28 - 27.25| = 0.75
|20 - 27.25| = 7.25
|30 - 27.25| = 2.75
Find the average of these absolute differences:
MAD = (6.25 + 5.25 + 3.25 + 1.25 + 0.25 + 0.75 + 7.25 + 2.75) / 8
= 26.75 / 8
= 3.34375
Rounded to the nearest whole number, the mean absolute deviation (MAD) of the given data set (21, 22, 24, 26, 27, 28, 20, 30) is 3.
50 apples cost $25. How much would 75 apples cost?
Answers
Answer:
$35
Step-by-step explanation:
Find the cost of 1 apple
$25/50 = 0.5
1 apple costs 50 cents/ 0.5 dollar
Multiply by 70 to find the cost of 70 apples
$0.5 x 70 apples = 35
$37.50. ...................
15. The line y = - 0.75x + 1.25 is tangent to a circle whose center is located at (2, 6) Find the tangent point and a second tangent point of a line with the same slope as the
Answers
The tangent point and a second tangent point of a line with the same slope as the given line are (2.67, 6) and (2.57, 6.1).
How to calculate the valueThe slope of the given line is -0.75.
The radius of the circle is |6 - 1.25| / -0.75 = 7.
The equation of the tangent line is y = -0.75x + c.
Substituting the coordinates of the center of the circle into this equation, we get 6 = -0.75 * 2 + c
Solving for c, we get c = 8.
The equation of the tangent line is y = -0.75x + 8.
The point of tangency is the point where the tangent line intersects the circle. To find the point of tangency, we need to solve the equation of the tangent line for x.
y = -0.75x + 8
6 = -0.75x + 8
-2 = -0.75x
x = 2.67
The point of tangency is (2.67, 6).
The second tangent point is the point where the tangent line intersects the circle at a different location. The direction of the tangent line is the same as the direction of the vector (-0.75, 1).
We can move the point of tangency a small distance in the direction of the tangent line by adding a small multiple of the vector (-0.75, 1) to the point of tangency.
Let's add a multiple of 0.1 to the point of tangency.
(2.67, 6) + 0.1 * (-0.75, 1)
= (2.57, 6.1)
The second tangent point is (2.57, 6.1).
Learn more about tangent on
https://brainly.com/question/30162650
#SPJ1
The line y = - 0.75x + 1.25 is tangent to a circle whose center is located at (2, 6) Find the tangent point and a second tangent point of a line with the same slope as the given line
The physical plant at the main campus of a large state university recieves daily requests to replace florecent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 55 and a standard deviation of 4. Using the empirical rule (as presented in the book), what is the approximate percentage of lightbulb replacement requests numbering between 51 and 55
Answers
Answer:
percentage of lightbulb replacement requests = 34.15 %
Step-by-step explanation:
According to Empirical Rule
interval %
μ ± σ 55 ± 4 ( 51 ; 59 ) 68.3
As the question is a percentage between 55 and 51
or between 51 and μ - σ by symmetry is 68.3/2
% of lightbulb replacement requests = 34.15 %
Please answer ASAP!! Fairly easy shapes question!!! Will give Brainliest

Answers
Answer:
Rectangle, Rhombus and Square
Similarity in diagonals :
★The diagonals bisect each other.3rd one is the right answer.
Answer:
The diagonals bisect each otherStep-by-step explanation:
The first choice is not applicable to rhombus- incorrectThe second choice is not applicable to rectangle- incorrectThe third choice is common for all three shapes - correctAn employee at a state park has 54 photos of animals found at the park. She wants to arrange the photos
in rows so that every row except the bottom row has the same number of photos. She also wants there to
be at least 5 rows.
Complete the description of two different ways she can arrange the photos.
photos or arrange the
She can arrange the photos as rows of 10 photos and 1 row of
photos as rows of 8 photos and 1 row of photos.
help, don’t ask me 2 use the calculator, mine doesn’t work ♀️♀️

Answers
Answer:
2.5
Step-by-step explanation:
10/4=2.5
Answer:
6,4,7,6
Step-by-step explanation:
Given m || n, find the value of x and y.
119°
to
yº
E
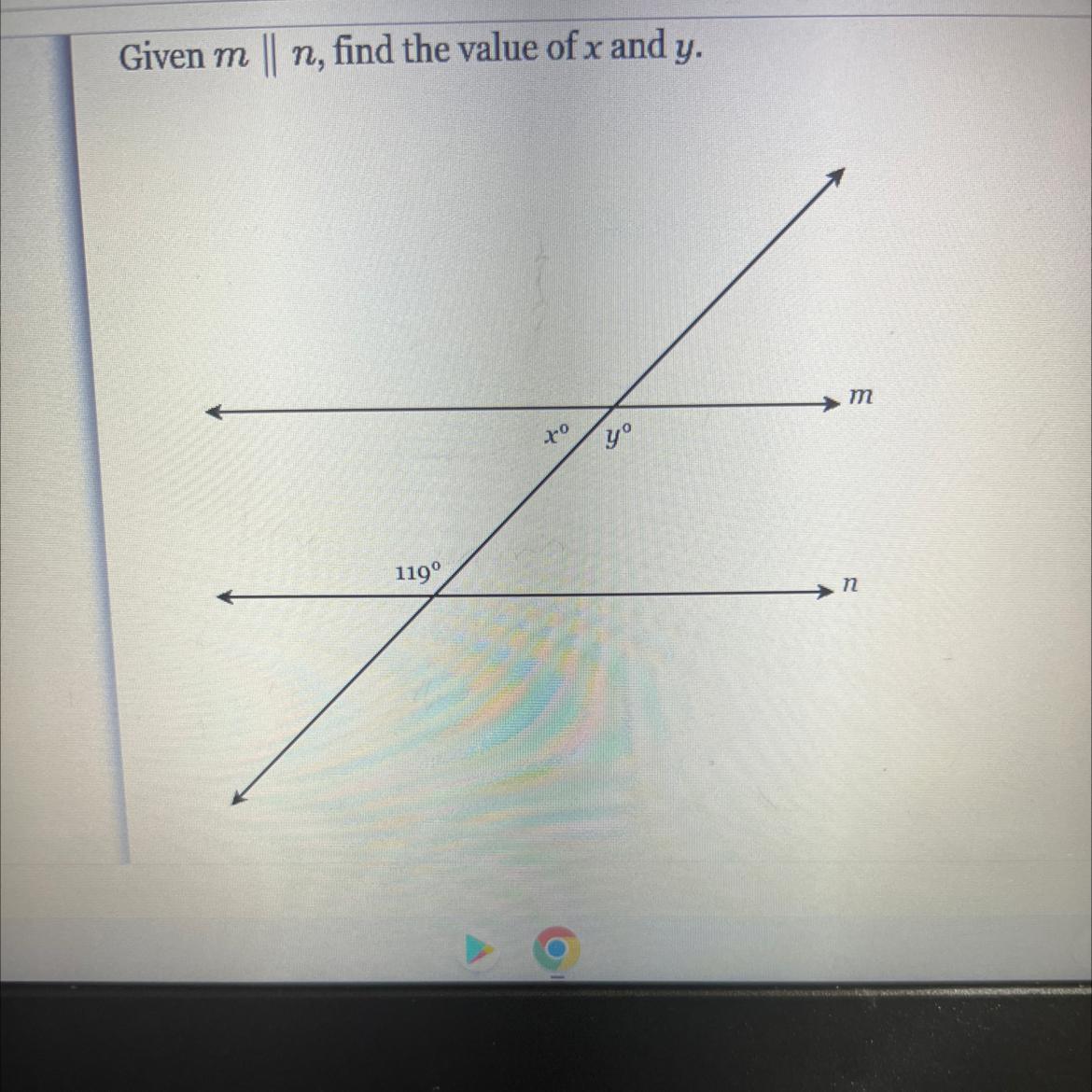
Answers
x+119°=180°(Co-interior angles are supplementary m || n)
\(x = 180 - 119 \\ x = 61\)
y=119°(alternate angles are equal m ||n)
GOODLUCK.
I need the answers to this assignment it’s one questions but multiple steps

Answers
Solution;
\(\begin{gathered} D=305-50P \\ \end{gathered}\)\(\begin{gathered} Solving\text{ for P;} \\ 50P=305-D \\ P=\frac{305}{50}-\frac{D}{50} \\ P=\frac{61}{10}-\frac{D}{50} \end{gathered}\)\(\begin{gathered} When\text{ D=240 pints;} \\ P=6.1-\frac{240}{50} \\ P=\text{ \$}1.3 \end{gathered}\)Find the perimeter of the
polygon if ZB = ZD.
11.5 cm
B
D
12.5 cm
13.5 cm

Answers
Answer:
100cm
Step-by-step explanation:
From the given diagram;
Perimeter of the polygon = AB + BC+ CD + DA
Perimeter of the polygon = 11.5 + 12.5 + 12.5 + 13.5 + 13.5 + 12.5 + 12.5 + 11.5
Perimeter of the polygon = 24 + 26 + 26 + 24
Perimeter of the polygon = 50 + 50
Perimeter of the polygon = 100cm
Hence the Perimeter of the polygon is 100cm
Answer:
100 cm
Step-by-step explanation:
An airplane can ascend at a rate of 54 1/2 meters in 1/3 second. How many meters can the airplane ascend in one second?
Answers
Answer:
163.5 meters in one second
Step-by-step explanation:
54.5 = 1/3m
multiply both sides by 3:
163.5 = m
The length of a triangle is eight more than twice its width. The perimeter is 88 feet. Find the dimensions of the rectangle.
Answers
Answer:
Length = 32 feet
Width = 12 feet
Step-by-step explanation:
From the question;
Width = w
Length = 2w + 8
But the perimeter of a rectangle = 2(l + b)
perimeter = 88 feet
88 = 2(2w + 8 + w)
88 = 2(3w + 8)
88 = 6w + 16
88 - 16 = 6w
72 = 6w
w = 72/6
w = 12 feet
Hence;
Length = 2(12) + 8 = 32 feet
Dimensions of the rectangle is;
Length = 32 feet
Width = 12 feet
Use each of the five digits $2, 4, 6, 7$ and $9$ only once to form a three-digit integer and a two-digit integer which will be multiplied together. What is the three-digit integer that results in the greatest product
Answers
Answer:
The 3 digit number 642 when multiplied 97 gives the greater product.
Step-by-step explanation:
The greatest product will result by multiplying the smaller 3 digit number with the greater two digit number.
The greater three digit number will be 976 and smaller 2 digit number would be 42
Multiplying
976*42 = 40992 ( descending order number)
679 *24= 16,296 ( ascending order number)
If we take the 2 digit number as 97 and 3digit number 642
Then multiplying
642* 97= 62,274 ( descending order number)
246 * 79=19434 ( ascending order number)
The 3 digit number 642 when multiplied 97 gives the greater product.
a survey firm wants to ask a random sample of adults in ohio if they support an increase in the state sales tax from 5.75% to 6%, with the additional revenue going to education. let denote the proportion in the sample who say that they support the increase. suppose that 40% of all adults in ohio support the increase. if the survey firm wants the standard deviation of the sampling distribution of to equal 0.01, how large a sample size is needed?
Answers
The survey firm needs a random sample of approximately 2401 adults in Ohio to achieve a standard deviation of 0.01 in the sampling distribution of the proportion of adults who support the increase in state sales tax.
To find the sample size needed, we can use the formula:
n = (z α/2 / E)^2 * p * (1-p)
where z α/2 is the z-score for the desired level of confidence (let's assume 95% confidence, so z α/2 = 1.96), E is the margin of error (in this case, 0.01), p is the estimated proportion (in this case, 0.4), and n is the sample size.
Plugging in these values, we get:
n = (1.96 / 0.01)^2 * 0.4 * (1-0.4)
n ≈ 9604
So the sample size needed is approximately 9604 adults in Ohio. This sample size should ensure that the standard deviation of the sampling distribution of the proportion who support the increase is no more than 0.01.
To determine the required sample size for the survey, we need to consider the proportion (p) of adults in Ohio who support the tax increase and the desired standard deviation (σ) of the sampling distribution. In this case, p = 0.40 and σ = 0.01.
The formula for the standard deviation of the sampling distribution of a proportion is:
σ = sqrt[(p * (1 - p)) / n]
Where n is the sample size.
To find the sample size, rearrange the formula:
n = (p * (1 - p)) / σ^2
Plug in the given values:
n = (0.40 * (1 - 0.40)) / 0.01^2
n ≈ 2401
Learn more about distribution here
https://brainly.com/question/4079902
#SPJ11
Prove that the following equation has exactly one solution in (−1,0):
x^5 + 5x + 1 = 0.
Answers
Prove that the equation \(x^5 + 5x + 1 = 0\) has exactly one solution in the interval (-1, 0).
To prove that the equation has exactly one solution in the given interval, we can use the Intermediate Value Theorem. According to this theorem, if a continuous function takes on different signs at two points in an interval, then it must have at least one root (solution) in that interval.
In this case, consider the function f(x) = \(x^5 + 5x + 1\). We can observe that f(-1) = -5 and f(0) = 1. Since f(-1) is negative and f(0) is positive, the function changes sign within the interval (-1, 0). Therefore, by the Intermediate Value Theorem, there must exist at least one root of the equation \(x^5 + 5x + 1 = 0\) in the interval (-1, 0).
To show that there is exactly one solution, we need to establish that the function does not change sign again within the interval. This can be done by analyzing the behavior of the function and its derivative. By studying the derivative, we can confirm that the function is increasing and crosses the x-axis only once in the given interval, ensuring that there is a single solution.
Therefore, we have proven that the equation \(x^5 + 5x + 1 = 0\) has exactly one solution in the interval (-1, 0).
Learn more about Theorem here:
https://brainly.com/question/30066983
#SPJ11
a logistic regression model of classifying the cancer patient from non cancer patient given by the mathematical function f(0.2 0.25*tumor dia 1.1*tumor coarseness). find the probability of a patient with tumour dia 5.5 and tumour coarseness of 0.7 to be a non cancer user ? (hint: consider sigmoid function)
Answers
the probability of a patient with a tumor diameter of 5.5 and tumor coarseness of 0.7 being a non-cancer patient is approximately 0.9106, or 91.06%.
To find the probability of a patient with a tumor diameter of 5.5 and tumor coarseness of 0.7 being a non-cancer patient using the logistic regression model with the given mathematical function, we need to apply the sigmoid function to the linear combination of the features.
The sigmoid function, also known as the logistic function, is defined as:
σ(z) = 1 / (1 + e^(-z))
where z is the linear combination of the features. In this case, the linear combination is given by:
z = 0.2 + 0.25 * tumor_diameter + 1.1 * tumor_coarseness
Substituting the values of tumor_diameter = 5.5 and tumor_coarseness = 0.7 into the equation, we get:
z = 0.2 + 0.25 * 5.5 + 1.1 * 0.7
z = 0.2 + 1.375 + 0.77
z = 2.345
Now, we can calculate the probability using the sigmoid function:
P(non-cancer) = σ(z) = 1 / (1 + e^(-2.345))
Calculating this value, we find that:
P(non-cancer) ≈ 0.9106
Therefore, the probability of a patient with a tumor diameter of 5.5 and tumor coarseness of 0.7 being a non-cancer patient is approximately 0.9106, or 91.06%.
to know more about probability visit:
brainly.com/question/32117953
#SPJ11
Please help with this inequalities problem attached below.

Answers
Answer:
1) A. 5 + 2.75 * S ≤ 21
2) 5
Step-by-step explanation:
Well there is an initial price of $5 and $2.75 per stop, and she can only spend less than or equal to $21 we can make the following inequality,
5 + 2.75 * S ≤ 21,
Meaning, Q.1 is A
Now #2 is 5 stops because if we plug in 5 for s we get 18.75.
Thus, the most amount of stops she can afford is 5.
Hope this helps :)
A study of 50 teenagers revealed that the average number of times they thought about food in one day was 100 times with a standard deviation of 10. Develop a 95% confidence interval of the mean times teenagers think about food in one day.
Answers
The 95% confidence interval for the mean times teenagers think about food in one day is (97.22, 102.78).
A study of 50 teenagers revealed that the average number of times they thought about food in one day was 100 times with a standard deviation of 10. Develop a 95% confidence interval of the mean times teenagers think about food in one day.
In order to develop the 95% confidence interval, we must determine the test statistics.
The z-test is used to determine the test statistics, and it is defined as the difference between the sample mean and the population mean divided by the standard deviation:
z = (X - μ) / (σ / √n)
Where, X = sample mean
μ = population mean
σ = standard deviation
n = sample size
Substitute the given values, σ = 10, n = 50, μ = 100.
Using the above formula, we can determine the test statistics,
z = (X - μ) / (σ / √n)
z = (100 - 100) / (10 / √50)
z = 0
Thus, the test statistics is 0. Now, we can use the test statistics and a z-table to find the critical value of z for a 95% confidence interval. The z-table indicates that the critical value of z for a 95% confidence interval is 1.96.
Using this value and the formula for the confidence interval, we can determine the 95% confidence interval of the mean times teenagers think about food in one day: CI = X ± (z * σ / √n)
CI = 100 ± (1.96 * 10 / √50)
CI = 100 ± 2.78
Therefore, the 95% confidence interval for the mean times teenagers think about food in one day is (97.22, 102.78).
Test Statistics: https://brainly.com/question/15110538
#SPJ11
Your friend loans you $20,000 for school. In five years he wants
$40,000 back. What is the interest rate he is charging you?
Remember to show your work.
Answers
The interest rate your friend is charging you for the $20,000 loan is 20% per year.
What is the interest rate on the loan?
The simple interest is expressed as;
A = P( 1 + rt )
Where A is accrued amount, P is principal, r is the interest rate and t is time.
Given that;
The Principal P = $20,000
Accrued amount A = $40,000
Elapsed time t = 5 years
Interest rate r =?
Plug these values into the above formula and solve for the interest rate r:
\(A = P( 1 + rt )\\\\r = \frac{1}{t}( \frac{A}{P} -1 ) \\\\r = \frac{1}{5}( \frac{40000}{20000} -1 ) \\\\r = \frac{1}{5}( 2 -1 ) \\\\r = \frac{1}{5}\\\\r = 0.2 \\\\\)
Converting r decimal to R a percentage
Rate R = 0.2 × 100%
Rate r = 20% per year
Therefore, the interest rate is 20% per year.
Learn more about simple interest here: brainly.com/question/25845758
#SPJ1
The marketing firm later conducted survey and found that 50 out of 500 sampled customers plan to purchased Ultra-HD television sets or game consoles in the next five years. What is the estimate of p, based on this survey
Answers
Based on the survey, the estimated proportion (p) of customers planning to purchase Ultra-HD television sets or game consoles in the next five years is approximately 0.1 or 10%.
The estimate of p, the proportion of customers who plan to purchase Ultra-HD television sets or game consoles in the next five years, can be calculated by dividing the number of customers who plan to purchase by the total number of sampled customers.
In this case, the survey found that 50 out of 500 sampled customers plan to purchase. Therefore, the estimate of p is 50/500, which simplifies to 0.1 or 10%.
Hence, the estimate of p, based on this survey, is 0.1 or 10%.
You can learn more about Ultra-HD television at
https://brainly.com/question/15686442
#SPJ11