You invest $3000 into an account that has a 3.7% annual
interest rate and is compounded monthly. How long will it
take until you have doubled your money?

Answers
Option C is correct. It will take about 18.76 years for the money to double
The formula for calculating the compound interest is expressed as:
A = P(1+r/n)ⁿˣ
A is the amount after the time x
P is the amount invested
r is the rate
n is the time of compounding
x is the time taken in years
Given the following
P = $3000
r = 3.7% = 0.037
x = ?
A = $6000(money doubled after x years)
n = 1/12 (monthy)
Substitute the given parameters into the formula above
6000 = 3000(1+0.037/12)^nx
6000/3000 = (1+0.00308)^12x
2 = 1.00308^12x
Take the log of both sides
log 2 = log1.00308^12x
0.3010 = 12x log 1.00308
12x = 0.3010/log 1.00308
12x = 0.3010/0.001336
12x = 225.47
x = 225.47/12
x = 18.76 yrs
Hence it will take about 18.76 years for the money to double
Learn more here: https://brainly.com/question/18442810
Related Questions
-29 19/40 as a decimal
Answers
Drag the expressions to the correct functions. Not all expressions will be used.
Consider the functions fand g.
= 4x² + 1
g(x) =
Perform the function compositions:
x² - 3
Answers
The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)).
Let the functions be f(x) = 4x² + 1 and g(x) = x² - 3
The correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
What is composition function?The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)). In this operation, the function g exists used for the outcome of applying the function f to x.
Given:
f(x) = 4x² + 1 and g(x) = x² - 3
a) (f o g)(x) = f[g(x)]
f[g(x)] = 4(x² - 3)² + 1
substitute the value of g(x) in the above equation, and we get
= 4(x⁴ - 24x + 9) + 1
simplifying the above equation
= 4x⁴ - 96x + 36 + 1
= 4x⁴ - 96x + 37
(f o g)(x) = 4x⁴ - 96x + 37
b) (g o f)(x) = g[f(x)]
substitute the value of g(x) in the above equation, and we get
g[f(x)] = (4x² + 1)²- 3
= 16x⁴ + 8x² + 1 - 3
simplifying the above equation
= 16x⁴ + 8x² - 2
(g o f)(x) = 16x⁴ + 8x² - 2.
Therefore, the correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
To learn more about the function refer to:
https://brainly.com/question/26709985
#SPJ9
there are 24 juice boxes in a pack, and 6 of them are fruit punch. what percent of the juice boxes are fruit punch?
Answers
if 269 are sampled, what is the probability that the sample proportion will differ from the population proportion by less than 0.03? round your answer to four decimal places.
Answers
The probability will be 0.9940.
The provided parameters are
p = 0.05 (the true proportion or the mean )
n = 269 ( sample size )
we can calculate standard deviation as follows
σ = \(\sqrt{\frac{p(1-p)}{n} }\)
σ = 0.0132
Now the values that 'x' can take are
x = \(x_{1}\) ± \(x_{2}\)
x = 0.05 + 0.03, 0.05 - 0.03
x = 0.08 , 0.02
Also the z-score is
z = (x - μ)/σ
z = \(\frac{0.08-0.05}{0.0132}\) , \(\frac{0.02-0.05}{0.0132}\)
z = 2.27 , -2.27
we now find the p-values for the z-scores
p values are = 0.9970 , 0.0030
The difference in these values will give the probability
∴ P = 0.9970 - 0.0030
P = 0.9940
learn more on central limit theorem here :
https://brainly.com/question/18403552
#SPJ4
The graph of a linear function passess through the points (3, 19) and (5, 23). Write an equation for the function. Show your work
Answers
Answer:
y = 2x +13
Step-by-step explanation:
1. find the slope by using the formula y2-y1
--------
x2-x1
which is
23 - 19 4
------------ = --- = 2
5-3 2
2. finding the y intercept
so to find the y intercept you plug in the numbers to this formula
y-y1 = m (x-x1)
y - 19 = 2 (x -3)
y - 19 = 2x -6
+19 +19
y = 2x +13
Identify the y-intercept for the function:
y=-3x
Answers
Answer:
0
Step-by-step explanation:
y-intercept: (0,0)
answer: (0,0)
If you take 2 steps every minute, how long will 20 steps take?
Answers
Answer:
10 minutes
Step-by-step explanation:
just divide 20 by 2 to get the minutes also WHO WALKS THAT SLOW?!??!?!
In a sale, the price of a book is reduced by 25%.
The price of the book in the sale is £12
Work out the original price of the book
Answers
Question: In a sale, the price of a book is reduced by 25%. The price of the book in the sale is £12. Work out the original price of the book
Answer: £16
Step-by-step explanation:
To determine the original price of the book, we can use the fact that the sale price is 75% (100% - 25%) of the original price. Let's denote the original price as x.
75% of x = £12
To solve for x, we can set up the equation:
0.75x = £12
To isolate x, we divide both sides of the equation by 0.75:
x = £12 / 0.75
x = £16
Therefore, the original price of the book was £16.
how much energy does a 180 calorie half-pint carton of chocolate milk store
Answers
A 180 calorie half-pint carton of chocolate milk stores approximately 753.72 joules of energy.
To determine the amount of energy stored in the 180 calorie half-pint carton of chocolate milk, we can convert the calories to joules. One calorie is approximately equal to 4.184 joules. Therefore, 180 calories is equal to 180 * 4.184 = 753.72 joules.
Calories are a unit of energy commonly used in nutrition to measure the energy content of food. However, in scientific calculations and physical contexts, the SI unit for energy is the joule. So, by converting the calories to joules, we can express the energy content of the chocolate milk carton in a standard unit. Hence, a 180 calorie half-pint carton of chocolate milk stores approximately 753.72 joules of energy.
LEARN MORE ABOUT energy here: brainly.com/question/1932868
#SPJ11
differentiate the following function g(x)3(x3-6)2(x2 4x-6)10
Answers
the derivative of function g(x) = \(3(x^3-6)^2(x^2 + 4x - 6)^{10} is:g'(x) = 3 * [2(x^3-6)(3x^2)(x^2 + 4x - 6)^{10} + (x^3-6)^2 * 10(x^2 + 4x - 6)^9(2x+4)]\)
To differentiate the function\(g(x) = 3(x^3-6)^2(x^2 + 4x - 6)^{10}\), we can use the chain rule and the power rule for differentiation.
Let's break it down step by step:
1. Start by differentiating the outermost function with respect to x. The outermost function is\((x^3-6)^2(x^2 + 4x - 6)^{10}\), which we'll call f(x). Let's denote it as \(f(x) = (x^3-6)^2(x^2 + 4x - 6)^{10}.\)
2. Differentiate f(x) using the product rule. Let's call the first factor (x^3-6)^2 and the second factor \((x^2 + 4x - 6)^{10}\). The derivative of f(x) is given by:
\(f'(x) = (2(x^3-6)(3x^2)) * (x^2 + 4x - 6)^{10} + (x^3-6)^2 * (10(x^2 + 4x - 6)^9(2x+4))\)
3. Simplify the expression:
\(f'(x) = 2(x^3-6)(3x^2)(x^2 + 4x - 6)^{10} + (x^3-6)^2 * 10(x^2 + 4x - 6)^9(2x+4)\)
4. Finally, substitute f(x) back into the expression to obtain the derivative of g(x):
g'(x) = f'(x) * 3
To know more about derivative visit:
brainly.com/question/29144258
#SPJ11
A seal is swimming in the ocean 5 feet below sea level. It dives down 12 feet to catch a fish. Then, the seal swims 8 feet up towards the surface with the fish. Where is the final position of the seal compared to the sea level?
Answers
The final position of the seal with the fish is 1 foot above sea level.
The final position of the seal with the fish is 1 foot above sea level. Here's the explanation: Initially, the seal is swimming in the ocean at 5 feet below sea level. Then it dives down 12 feet to catch a fish. So now the seal is 5 + (-12) = -7 feet below sea level.
Then, the seal swims 8 feet up towards the surface with the fish. So the seal has traveled up by 8 feet from -7 feet. That means its current depth is -7 + 8 = 1 foot above sea level.
To know more about position visit:-
https://brainly.com/question/13066441
#SPJ11
What is the equation f the line L that passes through the point (_2,2) and has slope 2? Select one: a.y = 2x + 5 b. y =2x -5 Cy = 2* - 2 d.y = 2x + 6
Answers
The equation of the line L that passes through the point (-2, 2) and has a slope of 2 is y = 2x + 6.
To find the equation of a line, we need to use the point-slope form, which is given by y - y₁ = m(x - x₁), where (x₁, y₁) represents a point on the line, and m is the slope. In this case, the given point is (-2, 2), and the slope is 2.
Substituting these values into the point-slope form, we get y - 2 = 2(x - (-2)), which simplifies to y - 2 = 2(x + 2). Distributing the 2 on the right side, we have y - 2 = 2x + 4.
To obtain the slope-intercept form of the equation, which is y = mx + b, we isolate y on the left side of the equation. Adding 2 to both sides, we get y = 2x + 6. Therefore, the equation of line L that passes through the point (-2, 2) with a slope of 2 is y = 2x + 6.
Learn more about line here:
https://brainly.com/question/21511618
#SPJ11
How much wrapping paper would you
need to cover the box below?

Answers
the Area of the required wrapping paper will be 624 cm².
What is the Surface area?The area or region that an object’s surface occupies is known as its surface area. Volume, on the other hand, refers to how much room an object has. There are numerous shapes and dimensions in geometry, including spheres, cubes, cuboids, cones, cylinders, etc. Each form has its own volume and surface area.
Given, a trapezoid prism, to find the area of required wrapping paper we need to find the surface area of the prism.
From the general formula of the area of the trapezoid prism:
The surface area of the trapezoid prism = 2(area of a trapezoid face) + sum of the area of all four side
In our case,
area of trapezoid face = 1/2(10 +6) *7
area of trapezoid face = 8*7 = 56
From the formula of the area of the rectangle:
Area of rectangle = length * width
Area of the first side = 16 * 8
Area of the first side = 128
Area of the second side = 6*16
Area of the second side = 96
Area of the third side = 16*8
Area of the third side = 128
Area of the fourth side = 16*10
Area of the fourth side = 160
Thus,
Area of trapezoid prism = 2 *56 + 160+128+128+96
Area of trapezoid prism = 624 cm²
Therefore, the Area of the required wrapping paper will be 624 cm².
Learn more about the Surface area here:
https://brainly.com/question/29298005
#SPJ1
Please help!!!!!!!! I will mark brainliest if right!!!! Explain

Answers
Answer:
They are not similar.
Step-by-step explanation:
The angles of a triangle add up to be 180°. If they were similar, the triangle angles would have to be 60°, 40°, and 80°. Because one of the angles is 81°, the triangles cannot be similar.
81° + 40° + 60° does not equal 180.
Write vector in exact component form \( \) given: \[ \theta=240^{\circ} \text { and } m a g=12 \] Must use (,) to create vector.
Answers
The vector in exact component form is (-6√3, -6).
The given angle is 240° and the magnitude is 12. We will be using the following formula to find out the vector component form. Here are the steps to find the vector component form:
Converting degrees to radians:
We know that 180° is equivalent to π radians.
Therefore,
1° = π/180 radians.
Thus,
240°
= 240 × π/180 radians
= 4π/3 radians.
Identifying the x and y components:
cos θ = x / mag
\(sin θ = y / ma\)
Substituting the given values in the above formulae, we get:
\(cos 240° \\= x / 12sin 240° \\= y / 12x \\= 12 cos 240°\)
\(y = 12 sin 240°\)
Writing the vector in component form:
vector = (x, y)
\(= (12 cos 240°, 12 sin 240°)\\= (-6√3, -6)\)
The vector in exact component form is (-6√3, -6).
To know more about equivalent visit:
https://brainly.com/question/25197597
#SPJ11
What is the number 0 gonna be?
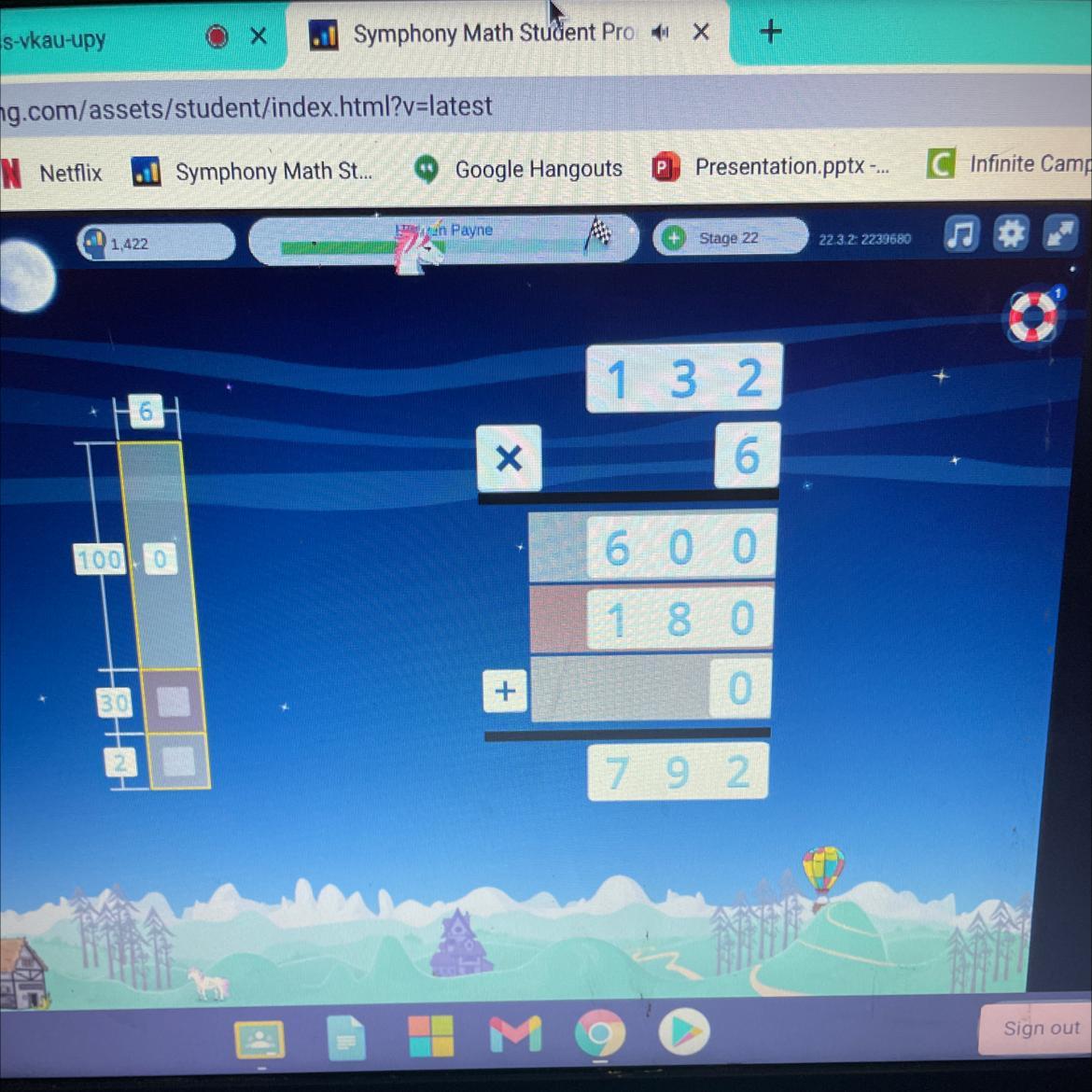
Answers
12 Step-by-step explanation:cause 6x2 = 12
Answer: change the number 0 to 2. the correct answer is 792 and 780.
Step-by-step explanation:
Find dy/dx and d2y/dx2.x = cos 2t, y = cos t, 0 < t < ?For which values of t is the curve concave upward? (Enter your answer using interval notation.)
Answers
The curve is concave upward on this interval. In interval notation, the answer is:(0, pi/2)
To find dy/dx, we use the chain rule:
dy/dt = -sin(t)
dx/dt = -sin(2t)
Using the chain rule,
dy/dx = dy/dt / dx/dt = -sin(t) / sin(2t)
To find d2y/dx2, we can use the quotient rule:
d2y/dx2 = [(sin(2t) * cos(t)) - (-sin(t) * cos(2t))] / (sin(2t))^2
= [sin(t)cos(2t) - cos(t)sin(2t)] / (sin(2t))^2
= sin(t-2t) / (sin(2t))^2
= -sin(t) / (sin(2t))^2
To determine where the curve is concave upward, we need to find where d2y/dx2 > 0. Since sin(2t) is positive on the interval (0, pi), we can simplify the condition to:
d2y/dx2 = -sin(t) / (sin(2t))^2 > 0
Multiplying both sides by (sin(2t))^2 (which is positive), we get:
-sin(t) < 0
sin(t) > 0
This is true on the interval (0, pi/2). Therefore, the curve is concave upward on this interval.
In interval notation, the answer is: (0, pi/2)
To know more about chain rule refer to
https://brainly.com/question/28972262
#SPJ11
WX=
In need of help thank!

Answers
the answer should be 12 if it isn't it's my bad
Here is a data set summarized as a stem-and-leaf plot: 3# | 023445777 4# | 0002223344467899 ## 07899 6 # 069 How many data values are in this data set? n=What is the minimum value in the last class? ans = What is the frequency of the modal class? (Hint, what is the mode?) frequency =How many of the original values are greater than 50 ? ans =
Answers
There are 29 data values in this data set. The minimum value in the last class is 60.
To determine the number of data values in the data set, we need to count the values represented in the stem-and-leaf plot. By examining the plot, we can count the values in each class and sum them up. In this case, there are a total of 29 data values in the data set.
To find the minimum value in the last class, we look at the rightmost leaf of the last stem in the stem-and-leaf plot. The last class is represented by the stem "6" and contains the values 60 and 69. Therefore, the minimum value in the last class is 60.
To determine the frequency of the modal class, we need to identify the class with the highest frequency. The mode represents the most frequently occurring value or class in the data set. In this case, the class with the highest frequency is the one with the stem "4" and the leaves "4, 4, 4, 6, 7, 8, 9, 9". The frequency of this class is 8, so the modal class has a frequency of 8.
To find the number of original values that are greater than 50, we examine the stem-and-leaf plot. We can see that all the values with stems greater than "5" are greater than 50. From the plot, we observe that there are 8 values in the "6#" class and 2 values in the "7#" class, totaling 10 values. Therefore, there are 10 original values in the data set that are greater than 50.
To learn more about data click here:
brainly.com/question/29117029
#SPJ11
calcular la altura del sol sobre el horizonte (medida en ángulo) si un edificio de 24 metros de altura proyecta una sobra de 30 metro

Answers
Usando propiedades de triangulos rectangulos veremos que el angulo de elevación es 38.65°
¿Como encontrar el angulo de elevacion del sol?
El ángulo de elevación del sol sera el angulo que esta en el vertice derecho del triangulo rectangulo en la imagen.
Sabemos que:
tan(a) = (cateto opuesto)/(cateto adjacente).
En este caso:
cateto opuesto = 24m
cateto adjacente = 30m
Entonces:
tan(a) = 24m/30m = 0.8
Aplicando la funcion inversa, obtenemos:
a = Atan(0.8) = 38.65°
Aprende más sobre triangulos rectangulos.
https://brainly.com/question/2217700
#SPJ1
(car sales) of the cars sold during the month of july, 87 had air conditioning, 99 had automatic transmission, and 73 had power steering. 8 cars had all three of these extras. 24 cars had none of these extras. 24 cars had only air conditioning, 64 cars had only automatic transmissions, and 35 cars had only power steering. 9 cars had both automatic transmission and power steering. how many cars had exactly two of the given options?
Answers
Cars with exactly two options = Total cars - Cars with none or one option - Cars with all three options. 8 cars had exactly two of the given options during the month of July.
To determine the number of cars that had exactly two of the given options (air conditioning, automatic transmission, and power steering), we can follow these steps:
1. Find the total number of cars sold in July.
2. Subtract the number of cars with none, one, or all three options to get the number of cars with exactly two options.
Step 1: Find the total number of cars sold in July
- 24 cars had none of the extras
- 24 cars had only air conditioning
- 64 cars had only automatic transmission
- 35 cars had only power steering
- 8 cars had all three extras
Total cars = 24 + 24 + 64 + 35 + 8 = 155 cars
Step 2: Subtract the number of cars with one or all three options
- 87 cars had air conditioning
- 99 cars had an automatic transmission
- 73 cars had power steering
- 8 cars had all three extras
Total cars with at least one option = 87 + 99 + 73 - 8 = 251 cars
Now, subtract the number of cars with none or one option from the total number of cars to find the number of cars with exactly two options:
Cars with exactly two options = Total cars - Cars with none or one option - Cars with all three options
Cars with exactly two options = 155 - (24 + 24 + 64 + 35) - 8 = 155 - 147 = 8 cars
Therefore, 8 cars had exactly two of the given options during the month of July.
Learn more about Month:
brainly.com/question/1248107
#SPJ11
A clay specimen, 25 mm thick, has been tested in an oedometer apparatus with two way rainage, and it is observed that 50% of the consolidation settlement occurs in 1 hour. A ayer of the same clay is observed to settle 10 mm in 10 years and after many years to settle (total primary consolidation) by 35 mm. Determine the thickness of the clay layer if it drains only from upper surface
Answers
The thickness of the clay layer, which drains only from the upper surface, can be determined based on the consolidation settlement observations. With 50% of consolidation settlement occurring in 1 hour for a 25 mm thick specimen, and a total primary consolidation settlement of 35 mm occurring over many years, the thickness of the clay layer is approximately 87.5 mm.
The consolidation settlement of a clay specimen can be used to estimate the thickness of a clay layer that drains only from the upper surface. In this case, the observed settlement data provides valuable information.
Firstly, we know that 50% of the consolidation settlement occurs in 1 hour for a 25 mm thick clay specimen. This is an important parameter for calculating the coefficient of consolidation (Cv) using Terzaghi's theory. From the Cv value, we can estimate the time required for full consolidation settlement.
Secondly, we are given that the same clay settles 10 mm over 10 years and eventually settles a total of 35 mm over a longer period. This long-term settlement is known as the total primary consolidation settlement. By comparing this settlement value with the settlement data from the oedometer test, we can determine the thickness of the clay layer.
To calculate the thickness, we can use the concept of the consolidation settlement ratio. The ratio of the total primary consolidation settlement to the consolidation settlement at 50% completion is equal to the ratio of the total thickness to the thickness at 50% completion. Applying this ratio, we can determine that the thickness of the clay layer, which drains only from the upper surface, is approximately 87.5 mm.
To learn more about thickness click here: brainly.com/question/23622259
#SPJ11
5. Write an expression to represent "Six more than the difference of a number and three."
Answers
i dot believe that is the correct answer have an amazing day love ;)
one end of a 10-foot ladder is 6 feet from the base of a wall. how high on the wall does the top of the ladder touch?
Answers
The top of the ladder touches a height of 8 feet on the wall. To determine how high on the wall the top of the ladder touches, we can use the Pythagorean theorem.
In this case, the ladder forms the hypotenuse of a right triangle, and the base of the wall and the height on the wall form the other two sides.
Let's denote the height on the wall as 'h'. According to the problem, one end of the ladder is 6 feet from the base of the wall, so the base of the triangle is 6 feet.
We can set up the equation using the Pythagorean theorem:
\((6)^2 + (h)^2 = (10)^2\)
Simplifying the equation:
36 + \(h^2\) = 100
\(h^2\) = 100 - 36
\(h^2\)= 64
Taking the square root of both sides:
h = √64
h = 8
Therefore, the top of the ladder touches a height of 8 feet on the wall.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
Use the general slicing method to find the volume of the following solid
The solid with a semicircular base of radius 15 whose cross sections perpendicular to the base and parallel to the diameter are squares The volume of the solid is __ cubic units.
(Type an exact answer)
Answers
The volume of the solid is approximately 807.08 cubic units.
Volume of Semicircular Solid w/Squared Cross-SectionsTo determine the volume of the solid, we can use the method of cylindrical shells.
Imagine taking a slice of the solid parallel to the base, with the cross-sectional area being a square of side length x (where x is a function of the height). The volume of this slice is the product of the square area and the height. The height of the slice is equal to the difference in the radii of two consecutive circular cross sections.
The radius of the larger circular cross-section can be found using the Pythagorean theorem, which states that the square of the hypotenuse (the radius) is equal to the sum of the squares of the other two sides (the height and half the side length of the square). Thus, we have:
r² = x² + (15-x)²
Solving for x, we get:
x = 15 * √(1 - (r/15)²)
The volume of the slice is then given by:
V = x² * (15 - x)
To find the total volume of the solid, we integrate this expression with respect to r from 0 to 15. The result is approximately 807.08 cubic units.
Learn more about Volume of Semicircular Solid w/Squared Cross-Sections here:
https://brainly.com/question/30485543
#SPJ4
The third term of an arithmetic sequence is 15 and when 20 is added to the third term the
8 term is obtained
a) What is the common difference of the sequence?
S
b) What is the position of 103 in this sequence?
Answers
Answer:
Common difference = 4
Position of 103 = 25th term
Step-by-step explanation:
a)
According to the given information:
\( a_3 + 20 = a_8\)
\( a+ (3-1)d + 20 = a+ (8-1)d\)
\( \cancel a+ 2d + 20 = \cancel a + 7d\)
\( 2d + 20 = 7d\)
\( 20 = 7d-2d\)
\( 20 = 5d\)
\( d = \frac{20}{5}\)
\( \purple {\bold {d = 4}} \)
Common difference = 4
b)
\( \because a_3 = 15....(given) \)
\( \therefore a + (3-1)d = 15\)
\( \therefore a + 2d = 15\)
\( \therefore a + 2\times 4= 15\)
\( \therefore a + 8= 15\)
\( \therefore a = 15-8\)
\( \red{\bold {\therefore a = 7}} \)
\( \because a_n = a + (n - 1) d\)
\( \therefore 103 = 7 + (n - 1)4 \)
\( \therefore 103 - 7 = (n - 1)4 \)
\( \therefore 96 = (n - 1)4 \)
\( \therefore \frac{96}{4}= n - 1\)
\( \therefore 24= n - 1\)
\( \therefore 24+1= n\)
\(\blue{\bold {\therefore n = 25}} \)
So, the position of 103 in this sequence is 25th term.
HHHHHHEEEEEEEEELLLLLLLLLPPPPPP

Answers
Answer:8 over 4
Step-by-step explanation:
Rise over run
thompson and thompson is a steel bolts manufacturing company. their current steel bolts have a mean diameter of 135 millimeters, and a standard deviation of 5 millimeters. if a random sample of 42 steel bolts is selected, what is the probability that the sample mean would be greater than 135.4 millimeters? round your answer to four decimal places.
Answers
The probability that the sample mean exceeds 135.4 millimeters is approximately 0.1446.
You can use the central limit theorem to approximate the sample distribution of the sample mean.
The mean of the sample distribution is a rise to the population mean (135 mm)
the standard deviation of the test distribution is a rise to the population standard deviation isolated by the square root of the test measure, which is \(5/√42\) ≈ 0.7689 mm.
To find the probability that the sample mean is greater than 135.4 millimeters, use the sample distribution to standardize the sample mean and use the standard normal distribution. That is,
\(z = (x - μ) / (σ / √n) = (135.4 - 135) / (5 / √42) ≒ 1.0607\)
where x = sample mean, μ = population mean, σ =population standard deviation, n=sample size, and z =standard value.
The probability that the sample mean exceeds 135.4 millimeters can be found by using a standard normal distribution table or calculator,
to find the area to the right of the Z value of 1.0607. This range is approximately 0.1446 or 14.46%.
Therefore, the probability that the sample mean exceeds 135.4 millimeters is approximately 0.1446.
learn more about the central limit theorem
brainly.com/question/18403552
#SPJ4
A point on a straight line has an x-coordinate of 3 and a y-coordinate of 6. Is the
relationship between x and y proportional?
Yes, because 3 is proportional to 6.
Yes, because 3 is proportional to 3 + 6.
It cannot be determined. At least one other point on the line is needed
to determine if x is proportional to y.
A
B
C
D It cannot be determined. At least two other points on the line are needed
to determine if x is proportional to y.
Answers
It cannot be determined. At least one other point on the line is needed to determine if x is proportional to y
Given data ,
A point on a straight line has an x-coordinate of 3 and a y-coordinate of 6
Now , A single point on a straight line does not define the connection between x and y. We must evaluate the connection between x and y for several places on the line in order to establish if x is proportional to y.
As a result, the relationship between x and y cannot be inferred only from the supplied location (3, 6). To establish the proportionality between x and y, at least one more point on the line is required
Hence , the equation of line is solved
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ1
Given the expression 3(4²) + 4 + 16-9, which operation would you perform first?
A. 3x4
B. 4²
C. 4+ 16
D.
16-9
Answers
Answer: 4²
Step-by-step explanation:
There is some rule but just remember:
1. parenthesis
2. exponents
3. division/multiplication
4. subtraction/addition