You play a game that involves
spinning a wheel. Each section
of the wheel shown has the
same area. Use a sample space
to determine whether randomly
spinning blue and then green are
independent events.
Answers
Based on the sample space, randomly spinning blue and then green are dependent events.
Two events are independent if the occurrence of one event does not affect the probability of the other event occurring.
Let's assume the wheel has 8 sections, with 4 blue and 4 green sections. The sample space for spinning blue and then green is:
{B1G1, B1G2, B1G3, B1G4, B2G1, B2G2, B2G3, B2G4, B3G1, B3G2, B3G3, B3G4, B4G1, B4G2, B4G3, B4G4}
The probability of spinning blue on the first spin is 4/8 = 1/2. Now, if we spin blue on the first spin, there are 3 blue and 4 green sections left on the wheel, so the probability of spinning green on the second spin is 4/7.
Therefore, the probability of spinning blue and then green is:
P(B) * P(G|B) = (1/2) * (4/7) = 2/7
The probability of spinning green on the first spin is also 4/8 = 1/2. So the probability of spinning blue on the second spin is 3/6 = 1/2.
Therefore, the probability of spinning green and then blue is:
P(G) * P(B|G) = (1/2) * (1/2) = 1/4
Since the probability of spinning blue and then green is not equal to the product of the individual probabilities, these events are dependent.
To learn more about spinning please click on below link
https://brainly.com/question/8349045
#SPJ1
Related Questions
ill give u 50 points!!

Answers
Answer:
4. C
5. I think D
6. A
7. B
Step-by-step explanation:
I hope this is correct and it helped
5 is d
6 is a
7 is d
can you guys please help me on this?

Answers
x= -5
Step by step:
Multiply both sides by 5
-20 = 3x - 5
Add 5 to both sides
-15 = 3x
Divide both sides by 3
-5 = x
And that’s all
Hope this helps!
please help
1. If m∠5 = 42° and m∠1 = 117°, find m∠CDF.
2. Question 7 options:
If m∠3=73° and DG−→−⊥DF−→− find m∠FDE
3. In the diagram below, BC−→− bisects ∠FBE
If m∠ABF=(7x+20)°, m∠FBC=(2x−5)° and m∠ABC=159°, find the value of x.
4. In the diagram below, BC−→− bisects ∠FBE
If m∠DBC=(12x−3)°, m∠DBE=(5x+12)°, and m∠EBC=(3x+13)°, find m∠EBC
5. In the diagram below, BC−→− bisects ∠FBE
If m∠FBC=(10x−9)°, m∠CBE=(4x+15)°,find m∠FBE.





Answers
Answer:
See belowStep-by-step explanation:
#1m∠CDF = m∠5 + m∠1 = 42° + 117° = 159°#2m∠FDE = m∠FDG - m∠3 = 90° - 73° = 17°#3m∠ABC = m∠ABF + ∠mFBC
159 = 7x + 20 + 2x - 5159 = 9x + 159x = 159 - 159x = 144x = 144/9x = 16#4m∠EBC = m∠DBC - m∠DBE
3x + 13 = 12x - 3 - 5x - 123x + 13 = 7x - 157x - 3x = 13 + 154x = 28x = 7m∠EBC = 3*7 + 13 = 21 + 13 = 34°
#5m∠FBE = m∠FBC + m∠CBE and m∠FBC = m∠CBE
m∠FBE = 2m∠CBE
10x - 9 = 4x + 1510x - 4x = 15 + 96x = 24x = 4m∠FBE = 2*(4*4 + 15) = 2*31 = 62°
Which table represents viable solutions for y = 5x, where x is the number of tickets sold for the school play and y is the amount of money collected for the tickets?
A 2-column table with 4 rows titled School Play Tickets. The first column is labeled tickets (x) with entries negative 100, negative 25, 40, 600. The second column is labeled money collected (y) with entries negative 500, negative 125, 250, 3000.
A 2-column table with 4 rows titled School Play Tickets. The first column is labeled tickets (x) with entries negative 20, 20, 100, 109. The second column is labeled money collected (y) with entries negative 100, 100, 500, 545.
A 2-column table with 4 rows titled School Play Tickets. The first column is labeled tickets (x) with entries 0, 10, 51, 400. The second column is labeled money collected (y) with entries 0, 50, 255, 2000.
A 2-column table with 4 rows titled School Play Tickets. The first column is labeled tickets (x) with entries 5, 65, 80, 200. The second column is labeled money collected (y) with entries 25, 350, 400, 1000.
Answers
Answer:
I think the second table.
Step-by-step explanation:
Because it is the correct one.
Answer:
C on edg.
Step-by-step explanation:
C.
Find m Fraction form

Answers
Answer:
130
Step-by-step explanation:
In 1895, the first a sporting event was held. The winners prize money was 150. In 2007, the winners check was 1,163,000. (Do not round your intermediate calculations.)
What was the percentage increase per year in the winners check over this period?
If the winners prize increases at the same rate, what will it be in 2040?
Answers
The estimated winners' prize in 2040, assuming the same rate of increase per year, is approximately $54,680,580,063,400.
The initial value is $150, and the final value is $1,163,000. The number of years between 1895 and 2007 is 2007 - 1895 = 112 years.
Using the formula for percentage increase:
Percentage Increase = [(Final Value - Initial Value) / Initial Value] * 100
= [(1,163,000 - 150) / 150] * 100
= (1,162,850 / 150) * 100
= 775,233.33%
Therefore, the winners' check increased by approximately 775,233.33% over the period from 1895 to 2007.
To estimate the winners' prize in 2040, we assume the same rate of increase per year. We can use the formula:
Future Value = Initial Value * (1 + Percentage Increase)^Number of Years
Since the initial value is $1,163,000, the percentage increase per year is 775,233.33%, and the number of years is 2040 - 2007 = 33 years, we can calculate the future value:
Calculating this expression:
Future Value = 1,163,000 * (1 + 775,233.33%)^33
Using a calculator or computer software, we can evaluate this expression to find the future value. Here's the result:
Future Value ≈ $1,163,000 * (1 + 77.523333)^33 ≈ $1,163,000 * 47,051,979.42 ≈ $54,680,580,063,400
Therefore, based on the assumed rate of increase per year, the estimated winners' prize in 2040 would be approximately $54,680,580,063,400.
Learn more about Expressions click here :brainly.com/question/24734894
#SPJ11
Bianca uses 1/3 of clay to make 4 bowls. She uses the same amount of clay for each bowl. How much clay does Bianca use for each bowls
Answers
Answer:
1/12clay each bowl
Step-by-step explanation:
Since we know she used 1/3, simply divide 1/3 by 4 to get your answer.
1/3 / 4/1
1/3 * 1/4
1/12
1/12 is the amount of clay which Bianca use for each bowls
What is Division?A division is a process of splitting a specific amount into equal parts.
Given that Bianca uses 1/3 of clay to make 4 bowls.
Bianca uses the same amount of clay for each bowl.
We have to find the amount of clay does Bianca use for each bowls.
To find this we have to divide 1/3 by 4.
When a fraction is divided by whole number, the denominator of the fraction is multiplied with the whole number.
(1/3)/4
1/3×1/4
One divided by three times of one by four we get one by twelve.
1/12
Hence, 1/12 is the amount of clay which Bianca use for each bowls
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ3
I tried answering twice before I get it wrong, help please?

Answers
Answer:y=x
Step-by-step explanation:
Easy as that because im smart
Does not have an x intercept
7
Simplify 3x + 6y + X -Y
a) 4x+7y
b) 4x-5y
c) 10xy
d) 4x+5y
Question 7

Answers
Answer:
D would be your answer. I used my algebra calculator and it shows you step by step how to do the problem

wath is answers k+10=27
Answers
Answer:
k = 17
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Step-by-step explanation:
Step 1: Define
k + 10 = 27
Step 2: Solve for k
Subtract 10 on both sides: k = 17Please show work!! I'll give you brainliest
10. If the area of a parallelogram is 690.84 m2 and the height is 20.2 m, what is the length of the base?
Answers
Answer:
b=34.2m
Step-by-step explanation:
equation for area of parallelogram
a=b×h
in which b is the base(length) and h is the height
\(690.84 = b \times 20.2\)
\(b = \frac{690.84}{20.2} \)
b=34.2m
Kari has 20 points. This is 4 times as many points as Shane has.
How many points does Shane have?
Answers
Answer:
80
Step-by-step explanation:
20 × 4 = 80
Answer:it is five
Step-by-step explanation:just divide 20 by 4
Ted can clear a football field of debris in 3 hours. Jacob can clear the same field in 2 hours. When they work together, the situation can be modeled by the equation, where t is the number of hours it would take to clear the field together.
1/3+1/2=1/t
How long will it take Ted and Jacob to clear the field together?
Answers
Ted can clear a football field in 3 hours, while Jacob can clear it in 2 hours. When they work together, the time it takes to clear the field can be determined by solving the equation 1/3 + 1/2 = 1/t.
Let's consider the equation 1/3 + 1/2 = 1/t, where t represents the number of hours it would take Ted and Jacob to clear the field together. To solve for t, we need to find a common denominator for the fractions on the left-hand side. The least common multiple (LCM) of 3 and 2 is 6.
By multiplying the first fraction by 2/2 and the second fraction by 3/3, we can rewrite the equation as (2/6) + (3/6) = 1/t. This simplifies to 5/6 = 1/t.
To isolate t, we can take the reciprocal of both sides, giving us t/1 = 6/5. Cross-multiplying, we find t = 6/5 = 1.2.
Therefore, it will take Ted and Jacob 1.2 hours (or 1 hour and 12 minutes) to clear the football field together.
Learn more about equation here:
brainly.com/question/29538993
#SPJ11
Daniel's store sells football jerseys with the logos of each of the five local junior high teams. Daniel has 6000 football jerseys in stock, divided among the five schools as shown.
Answers
Answer:
1200 jerseys eachStep-by-step explanation:
Step one:
we are told that the total available jerseys are 6000
this number of jerseys is to be divided among 5 schools.
hence we want to solve for the number of jerseys each school will collect from the store.
Step two:
A way to go about this is to divide the total available jerseys at the store, by the number of schools
that is 6000/5= 1200
This shows that each of the schools will collect 1200 jerseys from the store.
Simplify the following equation and solve for m
2 (2m) + 4 (4m + 2) = 108
M=
Answers

The value of m from the equation 2 (2m) + 4 (4m + 2) = 108 is m = 5
The value of m = 5
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be A = 2 (2m) + 4 (4m + 2) = 108
Now , on simplifying the equation , we get
2 (2m) + 4 (4m + 2) = 108
4m + 4 ( 4m ) + 4 ( 2 ) = 108
4m + 16m + 8 = 108
20m + 8 = 108
Subtracting 8 on both sides of the equation , we get
20m = 100
Divide by 20 on both sides of the equation , we get
m = 5
Therefore , the value of m is 5
Hence ,
The value of m from the equation 2 (2m) + 4 (4m + 2) = 108 is m = 5
To learn more about equations click :
https://brainly.com/question/10413253
#SPJ5
joseph can ride his bike 32 miles in 5 hours. kyle can ride his bike 20 miles in 3 hours who would ride farther in 15 hours explain .
Answers
Lyndsey ordered her school supplies online. They were delivered to her house in the box shown below.
9 in
10 in
15 in
What is the volume of the box, in cubic inches?
Answers
Answer:
1350 cubic inches
Step-by-step explanation:
9*10*15
In a short sentences please, Prove that the sum of two rational numbers is rational. THANK YOU!!!
Answers
The sum of two rational numbers is rational because the sum of any two fractions with rational numerators and denominators can be expressed as a fraction with a rational numerator and denominator.
How does this work?A rational number is any number that can be expressed as a ratio of two integers, where the denominator is not equal to zero. For example, 1/2, -3/4, 6/5, and 0 are all rational numbers.
When we add two rational numbers together, we can use the following formula:
a/b + c/d = (ad + bc) / bd
where a, b, c, and d are integers and b and d are not equal to zero.
This formula tells us that the sum of two rational numbers is also a rational number. The numerator of the sum is found by cross-multiplying the fractions, and the denominator of the sum is found by multiplying the denominators.
For example, if we want to add 1/2 and 2/3 together, we can use the formula above:
1/2 + 2/3 = (1 x 3 + 2 x 2) / (2 x 3) = 7/6
Therefore, the sum of 1/2 and 2/3 is 7/6, which is also a rational number. This formula can be used to prove that the sum of any two rational numbers is also a rational number.
#SPJ1
A rational number is a number that can be written as \(\dfrac{a}{b}\) where \(a,b\in\mathbb{Z}\) and \(b\not=0\).
If one number is \(\dfrac{a}{b}\) and the other is \(\dfrac{c}{d}\), where \(b,d\not=0\), their sum is \(\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{ad+bc}{bd}\). Since the set of integers is closed under addition and multiplication, we can write that \(\dfrac{ad+bc}{bd}=\dfrac{e}{f}\) where \(e,f\in\mathbb{Z}\) and \(f\not=0\), thus proving the sum of two rational numbers is a rational number.
Expand and simplify
(x+2)(x-6)
Answers
x^2 - 6x + 2x - 12
Now simplify
x^2 - 4x - 12
The answer is x^2-4x-12
Answer:
\(→(x + 2)(x - 6) \\ = {x}^{2}- 6x + 2x - 12 \\ = \boxed{{x}^{2} - 4x - 12}\)
(x²-4x-12) is the right answer.Phone calls arrive at the rate of 48 per hour at the reservation desk for Regional Airways. (Round your answers to four decimal places.)
(a) Compute the probability of receiving two calls in a 5-minute interval of time.
(b) Compute the probability of receiving exactly 10 calls in 15 minutes.
(c) Suppose no calls are currently on hold. If the agent takes 5 minutes to complete the current call.
how many callers do you expect to be waiting by that time?
What is the probability that none will be waiting?
(d) If no calls are currently being processed, what is the probability that the agent can take 2 minutes for personal time without being interrupted by a call?
Answers
The probability of receiving two calls in a 5-minute interval is:
P(X = 2) = (e^-4 * 4^2) / 2! = 0.0902
The probability of receiving exactly 10 calls in 15 minutes is:
P(Y = 10) = (e^-12 * 12^10) / 10! = 0.1143
(a) Let X be the number of calls received in a 5-minute interval. The arrival rate of calls is 48/60 = 0.8 calls per minute. Then, X follows a Poisson distribution with mean λ = 0.8 * 5 = 4. The probability of receiving two calls in a 5-minute interval is:
P(X = 2) = (e^-4 * 4^2) / 2! = 0.0902
(b) Let Y be the number of calls received in a 15-minute interval. The arrival rate of calls is 48/60 = 0.8 calls per minute. Then, Y follows a Poisson distribution with mean λ = 0.8 * 15 = 12. The probability of receiving exactly 10 calls in 15 minutes is:
P(Y = 10) = (e^-12 * 12^10) / 10! = 0.1143
(c) Let Z be the number of callers waiting after 5 minutes. The arrival rate of calls is 48/60 = 0.8 calls per minute. Then, Z follows a Poisson distribution with mean λ = 0.8 * 5 = 4. The expected number of callers waiting after 5 minutes is:
E(Z) = λ = 4
The probability that none will be waiting is:
P(Z = 0) = e^-4 = 0.0183
(d) Let W be the waiting time until the next call. The time between calls follows an exponential distribution with rate λ = 48/60 = 0.8 calls per minute. Then, the probability that the agent can take 2 minutes for personal time without being interrupted by a call is:
P(W > 2) = e^(-0.8 * 2) = 0.4493
Alternatively, we can use the memoryless property of the exponential distribution to calculate:
P(W > 2) = P(W > 1 + 1) = P(W > 1) * P(W > 1) = e^(-0.8 * 1) * e^(-0.8 * 1) = 0.4493.
To learn more about exponential, refer below:
https://brainly.com/question/28596571
#SPJ11
The ratio of the price of a book to the price of a calculator is 5:2. If the price of the book drops by £5, the ratio will be 2:1. What is the price of the calculator?
Answers
Price of book / price of calculator = 5 / 2
Price of book - 5 / price of calculator = 2 / 1
Cross multiply and let x = price of book and let y = price of calculator
Price of book * 2 = price of calculator * 5
2x = 5y
Price of book - 5 * 1 = Price of calculator * 2
x - 5 = 2y
Those are now our two equations and we can solve for the variables now by rewriting the second equation to isolate y and then substitute that into y in the first equation to solve for x.
(x - 5) / 2 = y
y = .5x - 2.5
2x = 5(.5x - 2.5)
2x = 2.5x - 12.5
-.5x = -12.5
x = 25
Price of book is 25 dollars.
x - 5 = 2y
25 - 5 = 2y
20 = 2y
y = 10
Price of calculator is 10 dollars.
Hope this helps!
Find the volume of the solid enclosed by the paraboloids z=1(x2+y2) and z=18−1(x2+y2).
Answers
The volume of the solid here which is enclosed by paraboloids is 81π.
Use cylindrical coordinates.
z = x² + y² ==> z = r²
z = 18 - (x² + y²) ==> z = 18 - r².
Curve of intersection:
r² = 18 - r² ==> r = 3, a circle.
So, the volume ∫∫∫ 1 dV equals
∫(θ = 0 to 2π) ∫(r = 0 to 3) ∫(z = r² to 18 - r²) 1 * (r dz dr dθ)
= 2π ∫(r = 0 to 3) rz {for z = r² to 18 - r²} dr
= 2π ∫(r = 0 to 3) r(18 - 2r²) dr
= π ∫(r = 0 to 3) (36r - 4r³) dr
= π(18r² - r⁴) {for r = 0 to 3}
= 81π.
The intersecting curves that are transversally intersecting make up an intersection curve in most cases, which means that the surface normals are never parallel at any common point. This limitation does not apply in situations when the surfaces touch or share surface elements. The intersections of two revolution cylinders form the bicylindrical curves.
Learn more about Curve of intersection here brainly.com/question/17063275
#SPJ4
butchy is pouring concrete for a new patio. the perimeter of the patio is 60 ft. and the area is 200 sq. ft. What is the length and width of the patio?
Answers
The length and width of the patio will be 20 feet and 10 feet, respectively.
What is the area and perimeter of the rectangle?Assume L is the length and W is the width. Then the area is given as,
A = L × W
And the perimeter is given as,
P = 2(L + W)
Butchy is pouring cement for another deck. the border of the deck is 60 ft. also, the region is 200 sq. ft. Then the equation is given as,
2(L + W) = 60
L + W = 30 ...1
L × W = 200 ...2
From equations 1 and 2, then we have
L x (30 - L) = 200
L² - 30L + 200 = 0
L² - 20L - 10L + 200 = 0
(L - 20)(L - 10) = 0
L = 10, 20
Then the value of W will be
At L = 10,
W = 30 - 10
W = 20 feet
At L = 20
W = 30 - 20
W = 10 feet
The length and width of the patio will be 20 feet and 10 feet, respectively.
More about the area and perimeter of the rectangle link is given below.
https://brainly.com/question/16572231
#SPJ1
Given matrix A and matrix B. Use this matrix equation, AX=B, to determine the variable matrix X.
A=[3 2 -1]
[1 -6 4]
[2 -4 3]
B=[33]
[-21]
[-6]
Answers
To determine the variable matrix \(\displaystyle X\) using the equation \(\displaystyle AX=B\), we need to solve for \(\displaystyle X\). We can do this by multiplying both sides of the equation by the inverse of matrix \(\displaystyle A\).
Let's start by finding the inverse of matrix \(\displaystyle A\):
\(\displaystyle A=\begin{bmatrix} 3 & 2 & -1\\ 1 & -6 & 4\\ 2 & -4 & 3 \end{bmatrix}\)
To find the inverse of matrix \(\displaystyle A\), we can use various methods such as the adjugate method or Gaussian elimination. In this case, we'll use the adjugate method.
First, let's calculate the determinant of matrix \(\displaystyle A\):
\(\displaystyle \text{det}( A) =3( -6)( 3) +2( 4)( 2) +( -1)( 1)( -4) -( -1)( -6)( 2) -2( 1)( 3) -3( 4)( -1) =-36+16+4+12+6+12=14\)
Next, let's find the matrix of minors:
\(\displaystyle M=\begin{bmatrix} 18 & -2 & -10\\ 4 & -9 & -6\\ -8 & -2 & -18 \end{bmatrix}\)
Then, calculate the matrix of cofactors:
\(\displaystyle C=\begin{bmatrix} 18 & -2 & -10\\ -4 & -9 & 6\\ -8 & 2 & -18 \end{bmatrix}\)
Next, let's find the adjugate matrix by transposing the matrix of cofactors:
\(\displaystyle \text{adj}( A) =\begin{bmatrix} 18 & -4 & -8\\ -2 & -9 & 2\\ -10 & 6 & -18 \end{bmatrix}\)
Finally, we can find the inverse of matrix \(\displaystyle A\) by dividing the adjugate matrix by the determinant:
\(\displaystyle A^{-1} =\frac{1}{14} \begin{bmatrix} 18 & -4 & -8\\ -2 & -9 & 2\\ -10 & 6 & -18 \end{bmatrix}\)
\(\displaystyle A^{-1} =\begin{bmatrix} \frac{9}{7} & -\frac{2}{7} & -\frac{4}{7}\\ -\frac{1}{7} & -\frac{9}{14} & \frac{1}{7}\\ -\frac{5}{7} & \frac{3}{7} & -\frac{9}{7} \end{bmatrix}\)
Now, we can find matrix \(\displaystyle X\) by multiplying both sides of the equation \(\displaystyle AX=B\) by the inverse of matrix \(\displaystyle A\):
\(\displaystyle X=A^{-1} \cdot B\)
Substituting the given values:
\(\displaystyle X=\begin{bmatrix} \frac{9}{7} & -\frac{2}{7} & -\frac{4}{7}\\ -\frac{1}{7} & -\frac{9}{14} & \frac{1}{7}\\ -\frac{5}{7} & \frac{3}{7} & -\frac{9}{7} \end{bmatrix} \cdot \begin{bmatrix} 33\\ -21\\ -6 \end{bmatrix}\)
Calculating the multiplication, we get:
\(\displaystyle X=\begin{bmatrix} 3\\ 2\\ 1 \end{bmatrix}\)
Therefore, the variable matrix \(\displaystyle X\) is:
\(\displaystyle X=\begin{bmatrix} 3\\ 2\\ 1 \end{bmatrix}\)
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Write the standard equation of the circle with center (5,-4) and radius 3.
OA (-5)2 + (y + 42 =9
B. (x + 5)2 + (y-4)2 = 9
C. (x+4)2 = (y-5)2 = 3
D. (x+5)2 + (-4)2 =3

Answers
Answer:
A. (x - 5)^2 + (y + 4)^2 = 9
Step-by-step explanation:
The standard equation of a circle is in the form:
(x - h)^2 + (y - k)^2 = r^2
where (h, k) is the center and r is the radius. We can substitute what we have:
(x - 5)^2 + (y + 4)^2 = 9
Let A be a diagonalizable matrix whose eigen values satisfy that A2 = A + 1. Then A satisfies A) A² = A +1 B) A² = A + 2 C) A² = A D) A² = A + 1
Answers
D) A^2 = A + 1 this equation represents diagonal matrices with the same eigenvalues on the diagonal.
Let λ be an eigenvalue of the matrix A, and let v be the corresponding eigenvector. Since A is diagonalizable, we can write A = PDP^(-1), where D is the diagonal matrix containing the eigenvalues on the diagonal, and P is the matrix whose columns are the eigenvectors.
We know that A^2 = A + 1, so we can substitute A with its diagonalizable form:
(PDP^(-1))^2 = PDP^(-1) + 1.
Expanding the square and applying the matrix multiplication rules, we get:
PD^2P^(-1) = PDP^(-1) + 1.
Since D is a diagonal matrix, D^2 will have the eigenvalues squared on the diagonal. Therefore, we have:
P(D^2)P^(-1) = PDP^(-1) + 1.
Multiplying both sides by P^(-1) on the right, and by P on the left, we obtain:
D^2 = D + 1.
This equation holds because P^(-1)P = I (the identity matrix), and D and D^2 are diagonal matrices with the same eigenvalues on the diagonal.
Therefore, the correct answer is D) A^2 = A + 1.
Learn more about eigenvalues
FINANCE Rawan deposits $13,000 into an account that pays 2.6% annual interest
compounded every 6 months.
a. Write a function to represent the balance A in the account after t years.
b. What will be the balance after 4 years?
c. What will be the balance after 7.5 years?
Answers
a) Required function is \(A(t) = 13,000 \times (1.013)^{2t}\)
b) The balance after 4 years is $15,182.51.
c)The balance after 7.5 years is $16,802.59
a. What is the function represent the balance A in the account after t years?
The function to represent the balance A in the account after t years can be given by:
\(A(t) = P \times (1 + \frac{r}{n})^{(nt)}\)
where P is the principal amount (initial deposit), r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, P = $13,000, r = 2.6%, n = 2 (interest is compounded every 6 months), and t is the time in years.
Substituting these values into the formula,
\(A(t) = 13,000 \times (1 + \frac{ 0.026}{2})^{(2t)}\)
Simplifying the expression,
\(A(t) = 13,000 \times (1.013)^{2t}\)
b. To find the balance after 4 years, we can substitute t = 4 into the formula we derived above:
\(A(4) = 13,000 \times (1.013)^{(2 \times 4)} \\ = 13,000 \times (1.013)^8 \\ = 15,182.51\)
Therefore, the balance after 4 years is $15,182.51.
c. To find the balance after 7.5 years, we can substitute t = 7.5 into the formula we derived above:
A(t) = 13,000 × (1.013)¹⁵ = 16,802.59
Therefore, the balance after 7.5 years is $16,802.59.
Learn more about function here,
https://brainly.com/question/2833285
#SPJ9
Find the product of 32 and 46. Now reverse the digits and find the product of 23 and 64. The products are the same!
Does this happen with any pair of two-digit numbers? Find two other pairs of two-digit numbers that have this property.
Is there a way to tell (without doing the arithmetic) if a given pair of two-digit numbers will have this property?
Answers
Let's calculate the products and check if they indeed have the same value:
Product of 32 and 46:
32 * 46 = 1,472
Reverse the digits of 23 and 64:
23 * 64 = 1,472
As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.
To find two other pairs of two-digit numbers that have this property, we can explore a few examples:
Product of 13 and 62:
13 * 62 = 806
Reversed digits: 31 * 26 = 806
Product of 17 and 83:
17 * 83 = 1,411
Reversed digits: 71 * 38 = 1,411
As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.
For example, let's consider the pair 25 and 79:
A = 2, B = 5, C = 7, D = 9
The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.
Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.
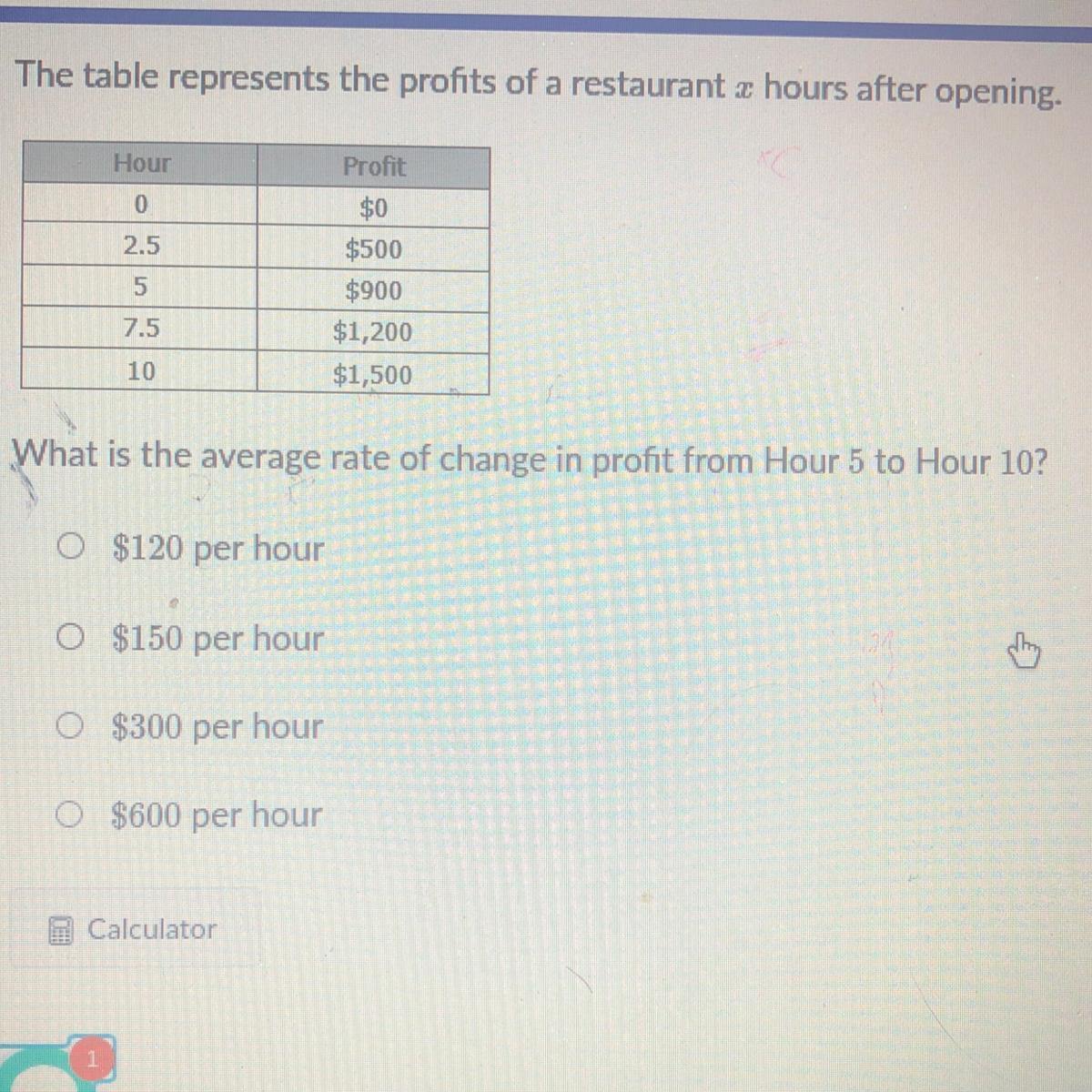
What is the average rate of change in profit from Hour 5 to Hour 10?
Answers
Answer:
d
Step-by-step explanation:
so at 5 hours he was at a profit of 900 and 5 hours later he is at a profit 1500 then you can sub tract 900 from 1500 which gives you 600
$600 is the average rate of change in profit from Hour 5 to Hour 10
What is Rate of change?A rate of change is a rate that describes how one quantity changes in relation to another quantity
The given table is
Hour Profit
0 $0
2.5 $500
5 $900
7.5 $1200
10 $1500
5 hours the profit is 900 and 5 hours later he is at a profit 1500
We need to subtract 900 from 1500 to find the average rate of change.
1500-900=600
Hence $600 is the average rate of change in profit from Hour 5 to Hour 10
To learn more on Rate of change click:
https://brainly.com/question/13103052
#SPJ2
Quiz
5
5x-2x = 7
x+y=7
Answers
Answer:
x= 7/3, y= 14/3
Step-by-step explanation:
5x-2x=7
x+y=7
Evaluate 5x-2x=7
5x-2x=3x
3x=7
divide both sides by 3
x=7/3
plug the x value into the second equation
7/3+y=7
subtract 7/3 from both sides
y=7-7/3
evaluate
21/3-7/3=14/3
x= 7/3, y= 14/3