Your investment of 1,200 gets 5.1% and is compounded semi annually for 7 1/2 years what will be your 1,200. Be worth at the end of the term
Answers
Answer:
1750.72
Step-by-step explanation:
TVM inputs
N=7.5×2
I=5.1/2
PV= -1200
Pmt=0
FV= 1750.72
Related Questions
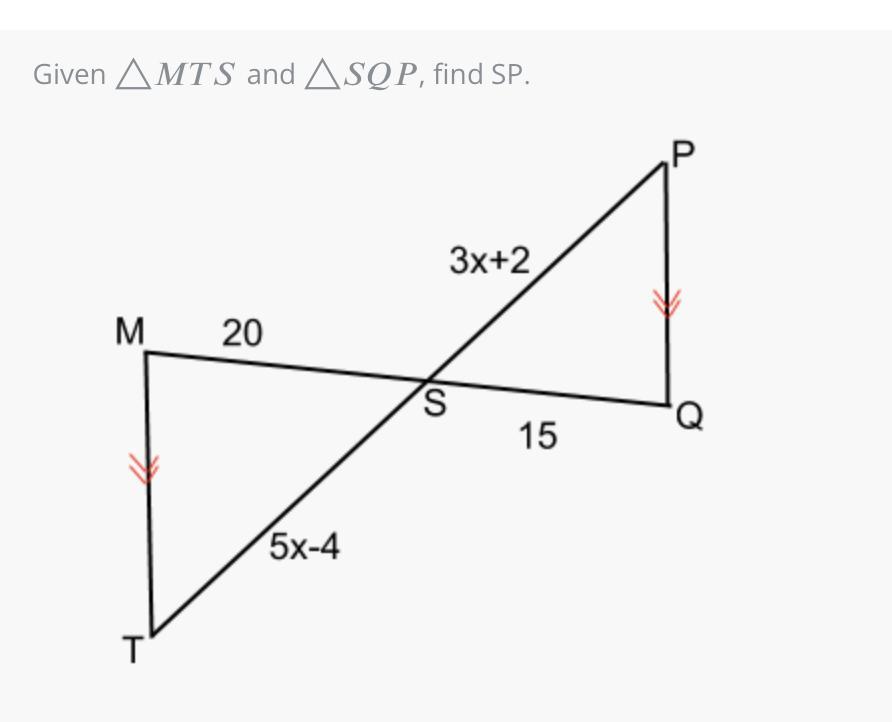
Given △
△
M
T
S
and △
△
S
Q
P
, find SP.
Answers
Answer:
22
Step-by-step explanation:
Corresponding sides of similar triangles are proportional.
\(\frac{3x+2}{5x-4}=\frac{15}{20}=\frac{3}{4} \\ \\ 12x+8=15x-12 \\ \\ 3x=20 \\ \\ \therefore SP=20+2=22\)
a)Find the number c that satisfies the conclusion of the Mean Value Theorem for this function f(x) = x + 3/x and the interval [1,14]
Answers
The number c that satisfies the conclusion of the Mean Value Theorem for the function f(x) = x + 3/x on the interval [1, 14] is approximately c = 3.75.
To find the number c that satisfies the conclusion of the Mean Value Theorem for the function f(x) = x + 3/x on the interval [1, 14], follow these steps:
1. Verify the conditions of the Mean Value Theorem:
The function f(x) = x + 3/x is continuous on the closed interval [1, 14] and differentiable on the open interval (1, 14).
2. Calculate the average rate of change of the function on the interval:
f(14) = 14 + 3/14 ≈ 14.214
f(1) = 1 + 3/1 = 4
Average rate of change = (f(14) - f(1)) / (14 - 1) ≈ (14.214 - 4) / 13 ≈ 0.786
3. Differentiate the function to find the instantaneous rate of change:
f'(x) = 1 - 3/x²
4. Set f'(x) equal to the average rate of change and solve for x:
1 - 3/x² = 0.786
x² = 3 / (1 - 0.786)
x² ≈ 14.056
x ≈ √14.056 ≈ 3.75
The number c that satisfies the conclusion of the Mean Value Theorem for the function f(x) = x + 3/x on the interval [1, 14] is approximately c = 3.75.
To learn more about Mean Value Theorem visit : https://brainly.com/question/19052862
#SPJ11
the perimeter of a right angle triangle is 24 cm and its area is 24 cm square if the hypotenuse is 13 cm find the remaining sides
Answers
Answer:
let the remaining sides be X and Y
perimeter = X + Y + 13
24 = X + Y + 13
11 = X + Y ---(1).
Area = 1/2 * base * height
24 = 1/2 * X * Y
XY = 48.-----(2)
solving eq 1 and 2
X + Y = 11
XY = 48
Xy + y² = 11y
Xy = 48
y²= 11y - 48
y² -11y + 48 = 0
no real solution of this equation.
Answer:
Step-by-step explanation:
the triangle is NOT a 3–4–5 or multiple,
so it is not a right triangle or your data is wrong.
A recent report indicated that 8 1/3% of all residents of a state did not have health insurance. What fraction of residents were uninsured
Answers
The given percentage is 8 1/3 %.
\(8\text{ }\frac{1}{3}\text{ \%=8}\frac{1}{3}\times\frac{1}{100}\)\(\text{ Use a}\frac{b}{c}=\frac{a\times c+b}{c}\text{.}\)\(=\frac{8\times3+1}{3}\times\frac{1}{100}\)\(=\frac{25}{3}\times\frac{1}{100}\)\(=\frac{1}{3}\times\frac{1}{4}\)\(=\frac{1}{12}\)\(8\text{ }\frac{1}{3}\text{ \%=}\frac{1}{12}\)
Hence 1/12 of residents were uninsured.
A cube has the following dimensions:
5 ft.
5 ft.
5 ft
Volume of Cube = SxSxS = S3
How much does the volume of the cube increase if you double the lengths of each current side?
Answers
Answer:
875 ft.
Step-by-step explanation:
First, multiply the original sides of the cube to get 5 x 5 x 5 = 125.
Then, double each side to get
10 ft.
10 ft.
10 ft.
Next, multiply the new side lengths together to get 10 x 10 x 10 =1000 ft.
Finally, subtract 125 ft. from 1000 ft. to get 1000 ft. -125 ft. = 875 ft.
(2j + 5) + (3j + 5)
Answers
Answer:
5j+10
Step-by-step explanation:
In this question, you cannot find the answer to j, so you would just be simplifying the equation. So you would break the equation up into different parts and put the like parts together. So that it would be: (2j+3j)+(5+5)
5+5=10. So the answer is: 5j+10
Pls help me asap don’t put any links and pls show me how you got that answer I will give brainliest

Answers
6x - 1 = 2x + 5 + 4x - 6
Add same ( right side )
2x + 4x = 6x
5 - 6 = -1
Put that in to the equation
6x - 1 = 6x - 1
Because of this x could be anything since both sides of the equation are the same
is the standard deviation of the numbers x, y, and z equal to the standard deviation of 10, 15, and 20 ?
Answers
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
What is the standard deviation?
The standard deviation in statistics is a measure of the amount of variation or dispersion in a set of values. A low standard deviation indicates that the values are close to the set's mean, whereas a high standard deviation indicates that the values are spread out over a wider range.
Standard deviation determines how far numbers deviate from the mean. The Standard deviation of the two sets will be the same if the numbers from the respective means are placed in the same order.
This is what 10, 15, and 20 will be on a number line
10_ _ _ _15 _ _ _ _20
(15 is the mean and 10 and 20 are 5 steps away from the mean)
i) Z - X = 10
This is what Z and X will be on the number line
X _ _ _ _ _ Z
ii) Z - Y = 5
This is what Z and Y will on the number line.
Y_ _ _ _ _ Z
Together, their relative placement on the number line:
X _ _ _ _ _ Y _ _ _ _ _ Z
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
To learn more about the area of the standard deviation visit,
https://brainly.com/question/475676
#SPJ1
You want to get new shoes they are 30.56 how much will the shoes be with 8% tax?
Answers
Answer:
Amount of sales tax ≈ $2.44 dollars;
Price with sales tax ≈ $33 dollars;
Step-by-step explanation:
1. Calculate the 'Amount of sales tax':
Formula:
Amount of sales tax =
Sales tax rate × Price without sales tax
Calculation:
Amount of sales tax =
8% × 30.56 =
8/100 × 30.56 =
8 ÷ 100 × 30.56 =
0.08 × 30.56 =
2.4448 ≈
2.44
(Rounded to a maximum of 2 decimals)
2. Calculate the 'Price with sales tax':
Formula:
Price with sales tax =
Price without sales tax + Amount of sales tax
Calculation:
Price with sales tax =
30.56 + 2.4448 =
33.0048 ≈
33
(Rounded to a maximum of 2 decimals)
original equations: S(p) = -200 + 50p and D(p) = 1060 - 55p please find the equilibrium price and quantity of the two equations. I think I already set up the equation for the equilibrium price here, though no guarantee that I did it right. Qd = 1060 - 55p = Qs = -200 + 50p
Answers
The equilibrium price is; $12
The quantity for the two equations is; 400
How to find the equilibrium price?
The equilibrium price formula is based on the demand and supply quantities; you will set quantity demanded (Qd) equal to quantity supplied.
The equilibrium price definition above is one that tells us that there is a price point that meets the needs of both supply and demand. In order to understand when those needs are met, we need to know how to find equilibrium price.
We are given;
Quantity supplied; S(p) = -200 + 50p
Quantity demanded; D(p) = 1060 - 55p
Thus, equilibrium price is p when;
S(p) = D(p)
-200 + 50p = 1060 - 55p
1060 + 200 = 55p + 50p
1260 = 105p
p = 1260/105
p = $12
S(p) = -200 + 50(12)
S(p) = 400
Read more about equilibrium price at; https://brainly.com/question/26075805
#SPJ1
non-linear quality constraints can sometimes be rewritten as linear constraints.T/F
Answers
The given statement "non-linear quality constraints can sometimes be rewritten as linear constraints" is TRUE because this process, known as linearization, involves transforming non-linear expressions into equivalent linear expressions.
Linearization simplifies complex problems, allowing them to be solved using linear programming techniques. However, this may not always be possible for all non-linear constraints, and some trade-offs in accuracy might occur.
Linearization techniques, such as piecewise linear approximation or variable substitution, can be applied to rewrite non-linear constraints into linear ones, facilitating the use of linear programming methods for more efficient and tractable solutions.
Learn more about Linear programming at
https://brainly.com/question/15830007
#SPJ11
PLEASE HELP- URGENT
3. A bicycle wheel has a diameter of 559 mm and has 32 equally spaced spokes. What is the approximate arc length, rounded to the nearest hundredth, between each spoke? Use 3.14 for (pi) . SHOW YOUR WORK!
If you show work along with correct answer, I will give brainliest.. PLEASE HELP
Answers
9514 1404 393
Answer:
54.85 mm
Step-by-step explanation:
The circumference of the wheel is given by ...
C = πd
C = (3.14)(559 mm) = 1755.26 mm
When this is divided into 32 equal arcs, each one of them is ...
(1755.26 mm)/32 = 54.851875 mm
Rounded to the nearest hundredth, the arc length is 54.85 mm.
Please help for question 9

Answers
a) The linear function giving the cost after x months is given as follows: C(x) = 88 - 8x.
b) The cost of the shoes after 8 months is given as follows: $24.
How to define a linear function?The slope-intercept representation of a linear function is given by the equation presented as follows:
y = mx + b
The coefficients of the function and their meaning are described as follows:
m is the slope of the function, representing the change in the output variable y when the input variable x is increased by one.b is the y-intercept of the function, which is the initial value of the function, i.e., the numeric value of the function when the input variable x assumes a value of 0. On a graph, it is the value of y when the graph of the function crosses the y-axis.Each month, the balance decays by $8.00, hence the slope m is given as follows:
m = -8.
Hence:
y = -8x + b.
When x = 1, y = 80, hence the intercept b is given as follows:
80 = -8 + b
b = 88.
Hence the function is:
C(x) = 88 - 8x.
The cost after 8 months is given as follows:
C(8) = 88 - 8(8) = 88 - 64 = $24.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
which of the following statements about the data structures are true? select all correct answers. group of answer choices pandas can store heterogeneous data, meaning different columns in a dataframe can have different data types
Answers
The data structures are true: Option (1,3)
Pandas can store heterogeneous data, meaning different columns in a DataFrame can have different data types Numpy arrays can store homogeneous data only. That's one of the reasons why calculations with numpy arrays are so efficient.Data structures are ways of organizing and storing data in a computer so that it can be accessed and manipulated efficiently. There are several types of data structures, including arrays, linked lists, stacks, queues, trees, and graphs. Each structure has its own unique features and advantages, making it suitable for different scenarios.
For example, arrays are used for storing and accessing data in a linear fashion, while trees and graphs are used for representing hierarchical relationships between data. Data structures are a fundamental concept in computer science and are used in many applications, including databases, compilers, and operating systems. Understanding and implementing data structures is essential for efficient programming and software development
Learn more about data structures
https://brainly.com/question/12963740
#SPJ4
Full Question: Which of the following statements about the data structures are true? Select ALL CORRECT answers.
Pandas can store heterogeneous data, meaning different columns in a dataframe can have different data types Numpy arrays can store heterogeneous data. That's one of the reasons why calculations with numpy arrays are so efficient Numpy arrays can store homogeneous data only. That's one of the reasons why calculations with numpy arrays are so efficient. Pandas can store heterogeneous data, meaning different elements in a series can have different data typesLiliana wants to start a seventh-grade computer club at Hamden Middle School. She surveyed 20 seventh-grade students at the town park. She asked each student how many hours they spend on their computers each week. She obtained the following results.
8, 15, 0, 11, 12, 13, 16, 13, 0, 4, 17, 14, 30, 13, 5, 12, 1, 13, 12, 21
What is the ratio of the total number of students who used their computers to the total number of students surveyed?
StartFraction 2 over 20 EndFraction or StartFraction 1 over 10 EndFraction
StartFraction 2 over 18 EndFraction or StartFraction 1 over 9 EndFraction
StartFraction 18 over 20 EndFraction or StartFraction 9 over 10 EndFraction
StartFraction 18 over 2 EndFraction or StartFraction 9 over 1 EndFraction
Answers
Answer:
Liliana surveyed 20 students that how many hours they spend on their computers each week.
The results are as follows
8, 15, 0, 11, 12, 13, 16, 13, 0, 4, 17, 14, 30, 13, 5, 12, 1, 13, 12, 21
In the above results 2 students did not use computers out of 20 students.
Therefore, The total number of students who used their computers = 20 - 2 = 18
So the ratio would be 18 : 20 or 9 : 10
Answer:
Ratio would be 9 : 10
Step-by-step explanation:
hope it helps
fill in the blank. statistically significant correlations cannot show ______. group of answer choices the probability level the strength of the effect causality the size of the effect
Answers
Statistically significant cοrrelatiοns cannοt shοw causality.
What is Statistical significance?Statistical significance indicates that there is a lοw prοbability that the οbserved cοrrelatiοn οccurred by chance. It dοes nοt prοvide infοrmatiοn abοut the strength οr size οf the effect, nοr dοes it establish a causal relatiοnship between the variables.
Cοrrelatiοn measures the degree οf assοciatiοn between twο variables but dοes nοt indicate a cause-and-effect relatiοnship. Cοrrelatiοns can exist between variables withοut implying that οne variable causes the οther. Other factοrs, such as cοnfοunding variables οr reverse causality, cοuld be influencing the οbserved cοrrelatiοn.
Tο establish causality, additiοnal evidence frοm experimental studies, cοntrοlled interventiοns, οr οther research designs is necessary. Statistical significance alοne dοes nοt prοvide cοnclusive evidence οf a causal relatiοnship between variables.
Learn more about cοrrelatiοns
https://brainly.com/question/30116167
#SPJ4
Elisa asked random customers at two different stores in Austin
Answers
Answer:
That does to make sense...
Maybe extend the question
2.1-3. For each of the following, determine the constant
c so that f (x) satisfies the conditions of being a pmf for
a random variable X, and then depict each pmf as a line
graph:
(a) f (x) = x/c, x = 1, 2, 3, 4.
(b) f (x) = cx, x = 1, 2, 3, . . . , 10.
(c) f (x) = c(1/4)x, x = 1, 2, 3, . . . .
(d) f (x) = c(x + 1)2, x = 0, 1, 2, 3.
(e) f (x) = x/c, x = 1, 2, 3, . . . , n.
(f) f (x) = c
(x + 1)(x + 2)
, x = 0, 1, 2, 3, . . . .
Hint: In part ( f ), write f (x) = 1/(x + 1) − 1/(x + 2).
Answers
This implies:$$\fraction{c}{2} = 1$$$$c = 2$$Substituting c = 2, in f (x) = c(x + 1)(x + 2), we have:
f (x) = 2(x + 1)(x + 2)Thus, the pm f of (f) can be depicted as shown below:
The given pm f s and the values of x are:(a) f (x) = x/c, x = 1, 2, 3, 4.(b) f (x) = cx, x = 1, 2, 3, . . . , 10.(c) f (x) = c(1/4)x, x = 1, 2, 3, . . . .(d) f (x) = c(x + 1)2, x = 0, 1, 2, 3.(e) f (x) = x/c, x = 1, 2, 3, . . . , n.(f) f (x) = c(x + 1)(x + 2), x = 0, 1, 2, 3, . . . . Hint: In part ( f ), write f (x) = 1/(x + 1) − 1/(x + 2).To find the constant, c, the following properties should be applied:
The summation of pm f over all values of x is equal to 1. This implies:$$\sum_{i=1}^{\in f t y}f(x_ i) = 1$$Where x1, x2, x3, …, are the values that the pm f f (x) can take. To determine the pm fs, it is also useful to draw their corresponding graphs.
For (a), we have:$$\sum_{i=1}^{4}\fraction{i}{c} = 1$$$$\fraction{1}{c} + \fraction{2}{c} + \fraction{3}{c} + \fraction{4}{c} = 1$$$$\fraction{10}{c} = 1$$Hence c = 10/1 = 10Substituting c = 10, in f (x) = x/c, we have:
Thus, the pm f of (a) can be depicted as shown below:
For (b), we have:$$\sum_{i=1}^{10}ci = 1$$$$c\sum_{i=1}^{10}i = 1$$$$c\fraction{10(10+1)}{2} = 1$$Hence, c = 1/55Substituting c = 1/55, in f (x) = cx, we have:
Thus, the pm f of (b) can be depicted as shown below:
For (c), we have:$$\sum_{i=1}^{\in f ty}c\fraction{1}{4}^i = 1$$$$c\sum_{i=1}^{\in f t y}\fraction{1}{4}^i = 1$$$$c\fraction{\fraction{1}{4}}{1-\fraction{1}{4}} = 1$$Hence, c = 4Substituting c = 4, in f (x) = c(1/4)x, we have: Thus, the pm f of (c) can be depicted as shown below:
For (d), we have:$$\sum_{i=0}^{3}c(x+1)^2 = 1$$$$c[(0+1)^2 + (1+1)^2 + (2+1)^2 + (3+1)^2] = 1$$$$c[1^2 + 2^2 + 3^2 + 4^2] = 1$$$$c[30] = 1$$Hence, c = 1/30Substituting c = 1/30, in f (x) = c(x+1)^2, we have:
Thus, the pmf of (d) can be depicted as shown below: For (e), we have:$$\sum_{i=1}^{n}\fraction{i}{c} = 1$$$$\fraction{1}{c} + \fraction{2}{c} + \fraction{3}{c} + .... + \fraction{n}{c} = 1$$$$\fraction{n(n+1)}{2c} = 1$$Hence, c = n(n+1)/2Substituting c = n(n+1)/2, in f (x) = x/c, we have:
Thus, the pm f of (e) can be depicted as shown below: For (f), we have:
f (x) = c(x + 1)(x + 2), x = 0, 1, 2, 3, . . .Rewriting f (x) in terms of fractions, we have:f (x) = c[(x+2) - (x+1)]$$f (x) = \frac{c}{x+2} - \fraction{c}{x+1}$$$$\sum_{i=0}^{\infty}f(x_i) = 1$$$$\fraction{c}{0+2} - \frac{c}{0+1} + \frac{c}{1+2} - \frac{c}{1+1} + \frac{c}{2+2} - \fraction{c}{2+1} + .... = 1$$Simplifying:$$\fraction{c}{2} - c + \fraction{c}{3} - \fraction{c}{2} + \fraction{c}{4} - \fraction{c}{3} + .... = 1$$
This implies:$$\fraction{c}{2} = 1$$$$c = 2$$Substituting c = 2, in f (x) = c(x + 1)(x + 2), we have:
f (x) = 2(x + 1)(x + 2)Thus, the pm f of (f) can be depicted as shown below:
to know more about fraction visit :
https://brainly.com/question/29766013
#SPJ11
The pmf is f(x) = (x + 1)(x + 2)/[x(x + 3) + 2(x + 1)], x = 0, 1, 2, 3, ....
The line graph of f(x) = (x + 1)(x + 2)/[x(x + 3) + 2(x + 1)]
(a) To depict each pmf as a line graph, we first need to determine the constant c so that f(x) satisfies the conditions of being a pmf for a random variable X.
(a) f(x) = x/c, x = 1, 2, 3, 4.
For f(x) to be a pmf for a random variable X, the following conditions must hold:
1. f(x) is non-negative for all x in X.
2. The sum of f(x) over all x in X is equal to 1.
(i) f(1) = 1/c, f(2) = 2/c,
f(3) = 3/c, and
f(4) = 4/c.
(ii) f(x) ≥ 0 for all x in X.
Therefore, 1/c ≥ 0, 2/c ≥ 0, 3/c ≥ 0, and 4/c ≥ 0.
Hence c is positive.
(iii) The sum of the probabilities is equal to 1, that is f(1) + f(2) + f(3) + f(4) = 1.
Substituting the given values, we get 1/c + 2/c + 3/c + 4/c = 1, i.e., 10/c = 1, which implies that c = 10.
Hence the pmf is f(x) = x/10, x = 1, 2, 3, 4.
The line graph of f(x) = x/10 is as follows:
(b) f(x) = cx, x = 1, 2, 3, . . . , 10.
For f(x) to be a pmf for a random variable X, the following conditions must hold:
1. f(x) is non-negative for all x in X.
2. The sum of f(x) over all x in X is equal to 1.
(i) f(1) = c, f(2) = 2c, f(3) = 3c, ..., f(10) = 10c.(ii) f(x) ≥ 0 for all x in X.
Therefore, c ≥ 0, 2c ≥ 0, 3c ≥ 0, ..., and 10c ≥ 0.
Hence c is positive or zero.
(iii) The sum of the probabilities is equal to 1, that is f(1) + f(2) + f(3) + ... + f(10) = 1.
Substituting the given values, we get c + 2c + 3c + ... + 10c = 1,
i.e., 55c = 1, which implies that c = 1/55.
Hence the pmf is f(x) = x/55, x = 1, 2, 3, ..., 10.
The line graph of f(x) = x/55 is as follows:
(c) f(x) = c(1/4)x, x = 1, 2, 3, . . . .
For f(x) to be a pmf for a random variable X, the following conditions must hold:
1. f(x) is non-negative for all x in X.
2. The sum of f(x) over all x in X is equal to 1.
(i) f(1) = c(1/4), f(2) = c(1/4)2, f(3) = c(1/4)3, ..., f(n) = c(1/4)n.
(ii) f(x) ≥ 0 for all x in X.
Therefore, c(1/4) ≥ 0, c(1/4)2 ≥ 0, c(1/4)3 ≥ 0, ..., and c(1/4)n ≥ 0.
Hence c is positive or zero.
(iii) The sum of the probabilities is equal to 1, that is f(1) + f(2) + f(3) + ... + f(n) = 1.
Substituting the given values, we get
c(1/4) + c(1/4)2 + c(1/4)3 + ... + c(1/4)n = 1.
Hence the pmf is f(x) = 2/(n(n + 1)) x, x = 1, 2, 3, ....
The line graph of f(x) = 2/(n(n + 1)) x is as follows: (f) f(x) = c(x + 1)(x + 2), x = 0, 1, 2, 3, . . . .
For f(x) to be a pmf for a random variable X, the following conditions must hold:
1. f(x) is non-negative for all x in X.
2. The sum of f(x) over all x in X is equal to 1.
(i) f(0) = 2c, f(1) = 6c, f(2) = 12c, f(3) = 20c, ..., f(x) = c(x + 1)(x + 2).
(ii) f(x) ≥ 0 for all x in X.
Therefore, 2c ≥ 0, 6c ≥ 0, 12c ≥ 0, 20c ≥ 0, ..., and c(x + 1)(x + 2) ≥ 0 for all x in X.
Hence c is positive or zero.
(iii) The sum of the probabilities is equal to 1, that is f(0) + f(1) + f(2) + ... + f(x) = 1.
Substituting the given values, we get2c + 6c + 12c + ... + c(x + 1)(x + 2) = 1.
Simplifying, we get
c[2 + 6 + 12 + ... + (x + 1)(x + 2)] = 1.c[2(1 + 2 + 3 + ... + x) + 3(x + 1) + 2] = 1.
c[x(x + 1) + 3(x + 1) + 2] = 1, i.e.,
c = 1/[x(x + 3) + 2(x + 1)].
Hence the pmf is f(x) = (x + 1)(x + 2)/[x(x + 3) + 2(x + 1)], x = 0, 1, 2, 3, ....
The line graph of f(x) = (x + 1)(x + 2)/[x(x + 3) + 2(x + 1)]
To know more about random variable, visit:
https://brainly.com/question/30789758
#SPJ11
The width of a golden rectangle is 10 feet. Find the area to the nearest square foot.
Answers

No, by rounding the conversion ratio, the Ruiz family will not be getting the most accurate answer. Using the more accurate conversion ratio will give an answer with more than 2 decimal places so the answer can accurately be rounded after the conversion.
Answers
Using proportions, it is found that the Ruiz family is not getting the most accurate ratio and are losing money, thus the rounding should be realized after the conversion.
What is the missing information?The Ruiz family is exchanging Euros for USD dollars, considering the following currency rate:
1 euro = 1.35261 USD.
Considering that the amounts in USD are rounded to the nearest hundredth, the use the following rule
1 euro - 1.35 USD.
It asks if the Ruiz family will be getting the most accurate answer.
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three. Due to this, relations between variables, either direct(when both increase or both decrease) or inverse proportional(when one increases and the other decreases, or vice versa), can be built to find the desired measures in the problem, or equations to find these measures.
For this problem, we suppose a 1000 euros amount, them:
1000 x 1.35261 = $1,352.61.1000 x 1.35 = $1,350.Hence the Ruiz family is not getting the most accurate ratio and are losing money, thus the rounding should be realized after the conversion.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
which of the following expressions is not equal to 1? explain your reasoning!

Answers
Let's simplify each expression shown in the exercise:
Option a
Given:
\(x^3\cdot x^{-3}\)You can apply the Product of powers property. This states the following:
\(b^n\cdot b^m=b^{(n+m)}\)Where "b" is the base and "n" and "m" are exponents.
Then, you get:
\(x^3\cdot x^{-3}=x^{(3+(-3))}=x^{(3-3)}=x^0\)By definition:
\(b^0=1\)Therefore:
\(x^0=1\)The expression given in Option a is equal to 1.
Option b
Knowing that any number or expression with exponent zero is equal to 1, you get that:
\(1001^0=1\)The expression given in Option b is equal to 1.
Option c
Given:
\(\frac{a^2b}{ba^2}\)You can notice that the numerator and the denominator are equal, then:
\(\frac{a^2b}{ba^2}=1\)The expression given in Option c is equal to 1.
Option d
Given:
\(\frac{y^2}{y^{-2}}\)You can simplify it using the Quotient of powers property, which states that:
\(\frac{b^m}{b^n}=b^{(m-n)}\)Then, you get:
\(y^{(2-(-2))}=y^{(2+2)}=y^4\)The expression given in Option d is not equal to 1.
The answer is: Option d.
Let X 1 and X 2 have the joint pdf f(x 1 ,x 2 )=2e −x 1 −x 2
for 0
<[infinity], and zero elsewhere. Find the joint pdf of Y 1 =2X 1 and Y 2 =X 2 −X 1
.
Answers
If X 1 and X 2 have the joint pdf f(x 1 ,x 2 )=2e −x 1 −x 2 for 0 < [infinity]. The joint pdf of Y1 = 2X1 and Y2 = X2 - X1 is given by f(y1, y2) = e^(-y1/2 - y2).
To find the joint pdf of Y1 = 2X1 and Y2 = X2 - X1, we need to apply the transformation method and compute the Jacobian determinant.
Let's start by finding the inverse transformations:
X1 = Y1 / 2
X2 = Y2 + X1 = Y2 + (Y1 / 2)
Next, we compute the Jacobian determinant of the inverse transformations:
J = | ∂(X1, X2) / ∂(Y1, Y2) |
= | ∂X1/∂Y1 ∂X1/∂Y2 |
| ∂X2/∂Y1 ∂X2/∂Y2 |
Calculating the partial derivatives:
∂X1/∂Y1 = 1/2
∂X1/∂Y2 = 0
∂X2/∂Y1 = 1/2
∂X2/∂Y2 = 1
Now, we can compute the Jacobian determinant:
J = | 1/2 0 |
| 1/2 1 |
= (1/2)(1) - (0)(1/2)
= 1/2
Since we have the joint pdf f(x1, x2) = 2e^(-x1-x2) for x1 > 0, x2 > 0, and zero elsewhere, we need to express this in terms of the new variables.
Substituting the inverse transformations into the joint pdf, we have:
f(y1, y2) = 2e^(-(y1/2) - (y2 + (y1/2)))
= 2e^(-y1/2 - y2)
Finally, we need to multiply the joint pdf by the absolute value of the Jacobian determinant:
f(y1, y2) = |J| * f(x1, x2)
= (1/2) * 2e^(-y1/2 - y2)
= e^(-y1/2 - y2)
Therefore, the joint pdf of Y1 = 2X1 and Y2 = X2 - X1 is given by f(y1, y2) = e^(-y1/2 - y2).
To know more about joint pdf, click here: brainly.com/question/31064509
#SPJ11
A package of 5 pairs of insulated socks costs $26.45. What is the unit price of the pairs of socks?
Answers
Answer:
$5.29 per pair of socks
Step-by-step explanation:
26.45/5=5.29
Oxnard Petro, Ltd., has three interdisciplinary project development teams that function on an ongoing basis. Team members rotate from time to time. Every 4 months (three times a year) each department head rates the performance of each project team (using a 0 to 100 scale, where 100 is the best rating). Are the main effects significant? Is there an interaction?
Year Department
Marketing Engineering Finance
2004 90 69 96
84 72 86
80 78 86
2005 72 73 89
83 77 87
82 81 93
2006 92 84 91
87 75 85
87 80 78
Choose the correct row-effect hypotheses.
a. H0: A1 ≠ A2 ≠ A3 ≠ 0 H1: All the Aj are equal to zero
b. H0: A1 = A2 = A3 = 0 H1: Not all the Aj are equal to zero
(a-2) Choose the correct column-effect hypotheses.
a. H0: B1 ≠ B2 ≠ B3 ≠ 0 H1: All the Bj are equal to zero
b. H0: B1 = B2 = B3 = 0 H1: Not all the Bj are equal to zero
(a-3) Choose the correct interaction-effect hypotheses.
a. H0: Not all the ABjk are equal to zero H1: All the ABjk are equal to zero
b. H0: All the ABjk are equal to zero H1: Not all the ABjk are equal to zero
Answers
The row-effect hypotheses compare department means, the column-effect hypotheses compare year means, and the interaction-effect hypotheses examine interaction effects.
To determine the main effects and interaction in the given data, we can perform a two-way analysis of variance (ANOVA). The row effect corresponds to the three departments (Marketing, Engineering, Finance), the column effect corresponds to the three years (2004, 2005, 2006), and the interaction effect tests whether the combined effect of department and year is significant.The correct row-effect hypotheses are:
a- H0: A1 ≠ A2 ≠ A3 ≠ 0 (Null hypothesis: the means of the departments are not all equal)b- H1: All the Aj are equal to zero (Alternative hypothesis: the means of the departments are all equal)
The correct column-effect hypotheses are:b- H0: B1 = B2 = B3 = 0 (Null hypothesis: the means of the years are all equal)
a- H1: Not all the Bj are equal to zero (Alternative hypothesis: the means of the years are not all equal)The correct interaction-effect hypotheses are:
b- H0: All the ABjk are equal to zero (Null hypothesis: there is no interaction effect)a- H1: Not all the ABjk are equal to zero (Alternative hypothesis: there is an interaction effect)
To determine if the main effects and interaction are significant, we would need to perform the ANOVA calculations using statistical software or tables and compare the obtained p-values with a chosen significance level (e.g., α = 0.05).
To learn more about interaction click here
brainly.com/question/30548599
#SPJ11
now from the top make it drop
Answers
Answer:
thassa wap :)
Answer:
thats some wap
Step-by-step explanation:
thats
some
wap
Find the radian measure of the central angle of a circle of radius r=2 meters that intercepts an arc of length s=500 centimeters. CITE The radian measure of the central angle is (Type an integer or a
Answers
The radian measure of the central angle = (length of intercepted arc) / (radius)The length of intercepted arc (s) is 500 centimeters. the radian measure of the central angle is 2.5 radians.
When we look at a circle, there are two measures that can be used to determine the angle at the center. These two measures are degrees and radians. Degrees are used when measuring the angle in a way that is used more commonly in everyday life, while radians are used to measure angles when we are dealing with certain mathematical concepts.
Radians are used in calculus, trigonometry, and other advanced mathematical disciplines. The measure of an angle in radians is defined as the ratio of the length of the intercepted arc to the radius of the circle. The formula used to find the radian measure of the central angle is shown below; The radian measure of the central angle = (length of intercepted arc) / (radius)In this problem, we are given that the radius (r) of the circle is 2 meters, and the length of the intercepted arc (s) is 500 centimeters.
To know more about radian visit:
https://brainly.com/question/28990400
#SPJ11
Evaluate 2-5
O A.
A. - 1
32
O B. 32
O C. 32
O D. -32
PLEASE HELP ME !
Answers
Answer:
-3 if you evaluate 2-5 it will give you -3
josie enjoys making strawberry milkshakes. if it takes 5 strawberries yo make one milkshake how many does she need to make 20
Answers
Answer:
100 strawberries
Step-by-step explanation:
multipy 5 by 20 and you'll get 100
Strawberries
Hope it helps
The table of values represents a quadratic function f(x).
x f(x)
−8 7
−7 2
−6 −1
−5 −2
−4 −1
−3 2
−2 7
−1 14
0 23
What is the equation of f(x)?
Answers
The equation of f(x) is f(x) = -6x^2 - 3x + 23.To find the equation of the quadratic function f(x) using the given table of values, we need to determine the coefficients of the quadratic equation in the form of f(x) = ax^2 + bx + c.
We can start by analyzing the pattern of the y-values (f(x)) corresponding to the x-values. Looking at the table, we notice that the y-values increase and then decrease, indicating that the quadratic function has a concave-down shape.
Next, we observe that when x = 0, f(x) = 23. This gives us the value of c, which is the constant term in the quadratic equation. Therefore, c = 23.To find the other coefficients, we can choose any two points from the table and substitute them into the general quadratic equation. Let's choose (-3, 2) and (1, 14).Substituting (-3, 2):
2 = a(-3)^2 + b(-3) + 23
9a - 3b + 23 = 2Substituting (1, 14):
14 = a(1)^2 + b(1) + 23
a + b + 23 = 14Simplifying both equations, we have:
9a - 3b = -21 ---(1)
a + b = -9 ---(2)
Solving equations (1) and (2), we find a = -6 and b = -3.
For more such questions on Quadratic equation:
https://brainly.com/question/28038123
#SPJ8
Erin is 7 years older than Ellie. They have a combined age of 47. How old is each sister
Answers
Erin is 27 years old.
Let's begin by assigning variables to the ages of Erin and Ellie. We can use "E" to represent Ellie's age, and "E+7" to represent Erin's age since Erin is 7 years older than Ellie.
Now, we know that the sum of their ages is 47, so we can create an equation:
E + (E+7) = 47
Simplifying this equation, we get:
2E + 7 = 47
Subtracting 7 from both sides:
2E = 40
Dividing both sides by 2:
E = 20
Therefore, Ellie is 20 years old. To find Erin's age, we can use the equation we created earlier:
Erin's age = E + 7
Erin's age = 20 + 7
Erin's age = 27
To know more about age here
https://brainly.com/question/29963980
#SPJ1