A car is traveling at 20(m)/(s) towards a stop sign and begins to brake when it is 30m from the sign. With what acceleration must the car brake in order to stop exactly at the sign (this is the minimum braking that must be applied to stop before going past the sign )?
Answers
To stop exactly at a stop sign located 30 meters away, a car traveling at 20 m/s must apply braking acceleration in order to come to a halt.
When a car applies the brakes, it experiences deceleration, which is negative acceleration. The goal is to determine the minimum braking acceleration needed for the car to come to a stop exactly at the stop sign, which is located 30 meters away.
To find the required acceleration, we can use the equation of motion:
\[v_f^2 = v_i^2 + 2a \cdot d\]
where \(v_f\) is the final velocity (zero in this case), \(v_i\) is the initial velocity (20 m/s), \(a\) is the acceleration (to be determined), and \(d\) is the distance (30 meters).
Rearranging the equation and substituting the given values:
\[0 = (20\, \text{m/s})^2 + 2a \cdot (30\, \text{m})\]
Solving for \(a\):
\[a = \frac{{-20^2}}{{2 \cdot 30}} = -\frac{400}{60} = -\frac{20}{3} \, \text{m/s}^2\]
Therefore, the car must apply an acceleration of \(-\frac{20}{3}\, \text{m/s}^2\) (negative sign indicating deceleration) in order to stop exactly at the stop sign.
Learn more about acceleration: brainly.com/question/460763
#SPJ11
Related Questions
Imagine a consumer is interested in purchasing new professional cloths for their first job out of college and they want to figure out how many pants (x) and shirts ( y ) to buy, and they know their preferences are represented by the following utility function: + U(x,y)=x
0.4
y
0.6
a) Calculate Marshallian Demand for pants b) Calculate Marshallian Demand for shirts c) Calculate Hicksian Demand for pants d) Calculate Hicksian Demand for shirts
Answers
The consumer's preferences are represented by the utility function \(U(x,y) = x^{0.4 }* y^{0.6}.\) We need to calculate the Marshallian demand for pants and shirts, as well as the Hicksian demand for pants and shirts.
a) To calculate the Marshallian demand for pants, we need to maximize the utility function U(x, y) subject to the consumer's budget constraint and the prices of pants and shirts. The Marshallian demand for pants (x*) can be found by taking the partial derivative of U(x, y) with respect to x and setting it equal to the ratio of the prices of pants and shirts \((P_x / P_y)\):
∂U/∂x =\(0.4 \times x^{(-0.6)} \times y^{0.6}\) = \(P_x / P_y\)
By rearranging the equation, we can solve for x* in terms of y:
\(x^* = (0.4 \times y^{0.6} \times P_x / P_y)^{(1/0.6)}\)
b) Similarly, to calculate the Marshallian demand for shirts, we take the partial derivative of U(x, y) with respect to y and set it equal to the inverse of the price ratio:
∂U/∂y =\(0.6 \times x^{0.4} \times y^{(-0.4) }= P_y / P_x\)
Solving for y*, we have:
y* =\((0.6 \times x^{0.4}\times P_y / P_x)^{(1/0.4)}\)
c) The Hicksian demand for pants (\(x_{hicks}\)) can be obtained by minimizing the expenditure function E(p, u) subject to the utility level u and the prices of pants and shirts. Since the utility function is Cobb-Douglas, the Hicksian demand for pants is the same as the Marshallian demand:
\(x_{hicks} = x^*\)
d) Similarly, the Hicksian demand for shirts \((y_{hicks})\) is also equal to the Marshallian demand for shirts:
\(y_{hicks }= y^*\)
Therefore, both the Hicksian demand and the Marshallian demand for pants and shirts are the same in this case.
Learn more about utility function here:
https://brainly.com/question/32733866
#SPJ11
Which is the slope of a line that is perpendicular to the line that passes through the points (-9, -4) and (3, 4)?
Answers
The needed slope, which traverses the points (-9, -4) and (3, 4) is 2/3.
What is the slope?The slope or gradient of a line in mathematics is a quantity that describes the line's steepness and direction.
The slope of a line can be used to gauge how steep it is.
Mathematically, the slope is calculated as "increase over run" (change in y divided by change in x).
So here are the key points:
(-9, -4) and (3, 4)
The slope equation is:
m = y2 - y1 /x2 - x1
Add values now, then compute as follows:
m = y2 - y1 /x2 - x1
m = 4 + 4 / 3 + 9
m = 8/12
m = 4/6
m = 2/3
Therefore, the needed slope, which traverses the points (-9, -4) and (3, 4) is 2/3.
Know more about the slope here:
brainly.com/question/29280886
#SPJ1
When building a house, the number of days required to build is inversely proportional to with the number of workers. One house was built in 36 days by 27 workers. How many days would it take to build a similar house with 9 workers?
Answers
It would take 108 days to build a similar house with 9 workers.
What is variation ?
In mathematics, variation refers to the concept of how one variable or quantity changes in relation to another variable or quantity. It can refer to a number of different concepts, including direct variation, inverse variation, joint variation, and partial variation. Direct variation is when one variable increases proportionally with another variable, while inverse variation is when one variable decreases proportionally with another variable. Joint variation is when one variable depends on multiple other variables, while partial variation is when one variable depends on some, but not all, of the other variables.
According to the question:
We can use the formula for inverse variation, which states that if two quantities x and y are inversely proportional, their product is constant:
x * y = k
where k is the constant of proportionality.
In this case, let d be the number of days required to build the house, and w be the number of workers. Then we have:
d * w = k
We know that one house was built in 36 days by 27 workers, so we can use this information to find k:
36 * 27 = k
k = 972
Now we can use this value of k to find how many days it would take to build a similar house with 9 workers:
d * 9 = 972
d = 972/9
d = 108
Therefore, it would take 108 days to build a similar house with 9 workers.
To know more about variation visit:
https://brainly.com/question/11928182
#SPJ1
question what is an expression equivalent to 6(24) using the distributive property? drag and drop the appropriate number into each box.
Answers
The following can be used to rewrite the provided expression: 6(24) = 6(20 + 4).
What in mathematics is a distributive property?The distributive Property states in that it is necessary to multiply every one of the two numbers by the factor before performing the addition operation when a factor is multiplied by that of the sum or addition of two terms. The distributive law, which states that in elementary algebra, equality is always true, is generalized by the distributive principle of binary operations.
According to the given data:The following generic form can be used to specify the distribution property:
a(b+c) = ab + bc
the following expression:
6(24)
We can observe the following by contrasting this to the general form:
a = 6
b + c = 24
Consequently, we must identify two integers from the options whose sum is 24.
These numbers, out of the options provided, are 20 and 4.
The following can be used to rewrite the provided expression: 6(24) = 6(20 + 4).
To know more about distributive property visit:
https://brainly.com/question/5637942
#SPJ4
5
Graph y = -2- 9.
y
9 -
8-
7
6-
4+
3-
2+
1+
-9-8-7 -6 -5 -4 3-2
2 3 4 5 6 7 8 9
-2 +
-3
-4+
-5
-6
-7+
-91
Answers
Answer:
6
Step-by-step explanation:
Vector vector u equals vector PQ has initial point P (2, 14) and terminal point Q (7, 3). Vector vector v equals vector RS has initial point R (29, 8) and terminal point S (12, 17). Part A: Write u and v in linear form. Show all necessary work. (4 points) Part B: Write u and v in trigonometric form. Show all necessary work. (8 points) Part C: Find 7u − 4v. Show all necessary calculations. (3 points)
Answers
The vectors presented in linear form using the coordinates of the points on the vectors are;
Part A; \(\vec{u}\) = <5, -11>, \(\vec{v}\) = <-17, 9>
Part B; \(\vec{u}\) = 12.08·(cos(-65.56°), sin(-65.56°)), \(\vec{v}\) = 19.24·9cos(-27.9°), cos(-27.9°)
Part C; 7·u - 4·v = <33, -41>
What is a vector?A vector is a quantity that has both magnitude and direction.
Part A;
The initial point of the vector u is; P(2, 14), and the final point of the vector u is Q(7, 3)
The vector u in linear form is therefore; \(\vec{u}\) = <7 - 2, 3 - 14> = <5, -11>
The initial point of the vector v is; R(29, 8), and the final point of the vector u is S(12, 17)
The vector v in linear form is therefore; \(\vec{v}\) = <12 - 29, 17 - 8> = <-17, 9>
Part B
Pythagorean Theorem indicates;
Magnitude of the vector u, |u| = √(5² + (-11)²) ≈ 12.08
The direction of the vector u is; arctan(-11/5) ≈ -65.56°
The vector in trigonometric form is therefore; \(\vec{u}\) = 12.08 × (cos(-65.56°), sin(-65.56°)
Magnitude of the vector v, |v| = √((-17)² + 9²) ≈ 19.24
The direction of the vector v is; arctan(9/(-17)) ≈ -27.9°
The vector in trigonometric form is therefore; \(\vec{v}\) = 19.24 × (cos(-27.9°), sin(-27.9°))
Part C;
7·u = <7 × 5, 7 × (-11)> = <35, -77>
-4·v = <(-4) × (-17), (-4) × 9> = <68, -36>
7·u - 4·v = <35 - 68, -77 - (-36)> = <33, -41>
Learn more on vectors here: https://brainly.com/question/28931875
#SPJ1
find the slope of the line that passes through 10, -8 1,12
Answers
Answer:
im really bad at math but here
Step-by-step explanation:
hi my
a $12$-slice pizza was made with only pepperoni and mushroom toppings, and every slice has at least one topping. only six slices have pepperoni, and exactly ten slices have mushrooms. how many slices have both pepperoni and mushrooms?
Answers
The terms with "x" cancel out, and we're left with:
0 = 12
6 + 10 + x + (12 - (6 + 10 + x)) = 12
Simplifying the equation, we have:
16 + x - (16 + x) = 12
The terms with "x" cancel out, and we're left with:
0 = 12
Let's denote the number of slices with both pepperoni and mushrooms as $x$. We are given that there are 6 slices with pepperoni and 10 slices with mushrooms.
Since every slice has at least one topping, the total number of slices is 12. We can break down the slices into the following categories:
Slices with only pepperoni: 6 slices
Slices with only mushrooms: 10 slices
Slices with both pepperoni and mushrooms: $x$ slices
Slices with neither pepperoni nor mushrooms: 12 - (6 + 10 + x) slices
We know that the total number of slices is 12, so we can write an equation:
6 + 10 + x + (12 - (6 + 10 + x)) = 12
Simplifying the equation, we have:
16 + x - (16 + x) = 12
The terms with "x" cancel out, and we're left with:
0 = 12
This equation is not possible to satisfy. Therefore, there must be an error or inconsistency in the given information. Please check the information provided again.
learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
Rewrite in simplest terms: -8(7y-8)-3(7y-7)
Answers
Answer:
−77y+85
I hope I helped!
Prove triangle ABD similar to triangle CBD.

Answers
Answer:
THANK YOU
Step-by-step explanation:
<3
Suppose a triangle has two sides of length 3 and 4 and that the angle
between these two sides is 60°. What is the length of the third side of the
triangle?
A. 5
B. 113
C. 413
D. 3
SUBMIT
Answers
when you are looking at a graph, you can say that average? why?
Answers
The average line shows the average of the data for a particular graph by drawing a line across the chart at the mean value points on the y-axis. By default, the average line label is displayed as a combination of line value and line title.
Definition of GraphicsGraph is a collection of data from several tables that will be presented or also displayed in the form of images, such as squares, circles, tubes, triangles, beams, cones or others. Graphics are also usually also interpreted as a framework or image that will be used to create a visualization object from data in tables with the aim of being able to provide information about a data from the material presenter to the recipient of the material.
In addition, graphs are also often interpreted as a description of the ups and downs of an existing data, or depicted by lines or pictures. The data used to create graphics can be in the form of numbers, letters, symbols, pictures, symbols, sayings, or paintings.
Learn more about graphic at https://brainly.com/question/10712002
#SPJ1
f(x) = x². What is g(x)?
g(x)
-5
-5
y
[f(x)/
(3, 3)
5
Click here for long description
A. g(x)=x²
OB. g(x) = x²
2
O c. g(x) = (3x)²
OD. g(x) = 3x²
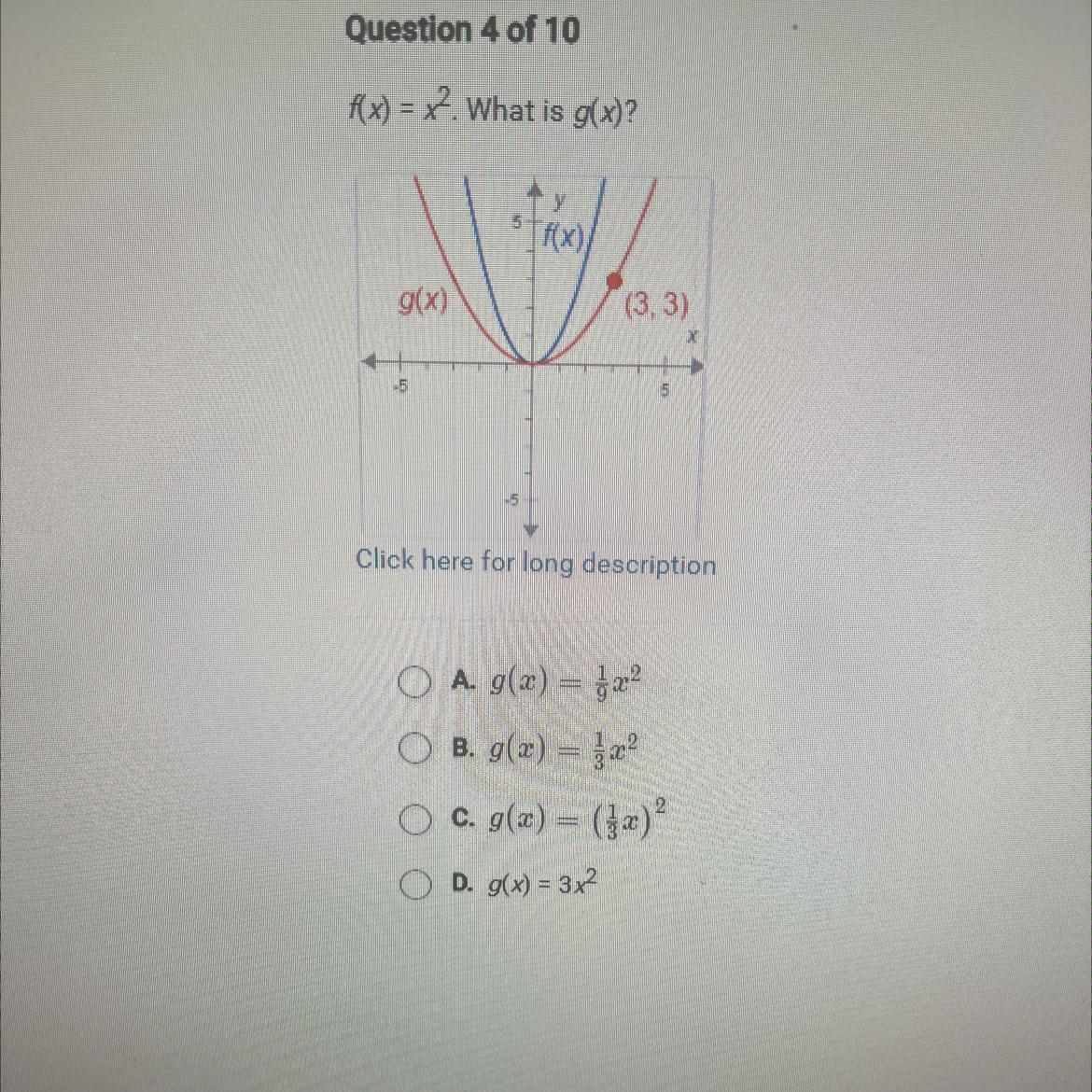
Answers
hello
the answer to the question is B)
explanation:
a point shown on the g(x) graph is (3,3)
if x = 3 and y = 3, therefore:
─ answer A) is incorrect
─ answer B) is the answer since:
(1/3)(x²) = (1/3)(9) = 3
─ answer C) is incorrect since:
((1/3)(x))² = ((1/3)(9))² = 9
─ answer D) is incorrect since:
3x² = 3 × 3² = 27
Grandma baked 96 cookies and gave them to her grandchildren. One of the grandchildren, Cindy, received c fewer cookies than she would have received had all of the cookies been evenly divided among the 8 grandchildren.How many cookies did Cindy receive
Answers
Answer:
12-c
Step-by-step explanation:
Let c be Cindy's cookies
Solution:
Each child should have gotten 12 cookies because 96/8 is 12 but Cindy got c less so the answer would be 12-c.
Which costs the most per ounce, 60 oz. of peanut butter for $5.40, 28 oz. for $2.24, or 16 oz. for $1.76? Explain how you got your answer.
Answers
Answer:
28 oz. for $2.24 cost most per ounce
$12.5 per oz
Step-by-step explanation:
Find the cost per ounce by dividing the total oz by cost of the total oz
60 oz. of peanut butter for $5.40
Cost per the ounce = 60 oz / $5.40
= $11.11 per oz
28 oz. for $2.24
Cost of peanut butter per ounce = 28 oz / $2.24
= $12.5 per oz
16 oz. for $1.76?
Cost of peanut butter per ounce = 16 oz / $1.76
= $9.10 per oz
28 oz. for $2.24 cost most per ounce
If x and y are in direct proportion and y is 6 when x is 9, find y when x is 3.
Answers
Answer: y = 2
Step-by-step explanation:
Direct proportion means that we can write an equation like
(9/6) = (3/y)
we want to isolate y, so multiply both sides by y.
9y/6 = 3
now multiply both sides by 6
9y = 18
y = 2
y = 2 when x is 3
PLSSSSSSS HELP ME CORRECT ANSWER

Answers
Answer:
8 units
Step-by-step explanation:
The formula for the area of a parallelogram is base * height = area. You have that the height = 5 and the area = 40, so that means base * 5 = 40.
If base * 5 = 40, you know that base = 8. You can also solve this like an equation:
b * 5 = 40
divide both sides by 5
b = 40/5 = 8 units
Answer: 8 units
uwu ur mom i hate flagotgs fr THAT IS A JOKE NO I DONT PLWAASE IMSS EORRY
A district restaurant manager bought 4 cases of disposable cups for $150 each. Each case contained 3,600 cups. He wants to split the cups equally between 6 restaurants. Which calculation yields the number of cups for each restaurant?.
Answers
The district restaurant manager divided 3,600 cups among six restaurants, giving each restaurant 600 number of cups.
The district restaurant manager divided 3,600 cups among six restaurants, giving each restaurant 600 cups. The district restaurant manager purchased four cases of disposable cups, each costing $150 and containing 3,600 cups. He needed to split the cups among six restaurants. To determine how many cups each restaurant would receive, he divided 3,600 by 6. This gave him an answer of 600 cups for each restaurant.
3,600 ÷ 6 = 600 cups
The district restaurant manager divided 3,600 cups among six restaurants, giving each restaurant 600 number of cups.
Learn more about number here
https://brainly.com/question/10547079
#SPJ4
Choose values for A and B to create infinitely many solutions to this system of equations.
Answers
To create infinitely many solutions to this system of equations, select values for A and B. The given system of equations is as follows: 2x - 3y = A and 4x - 6y = B.The first equation can be obtained by multiplying the second equation by 1/2.
Therefore, any value of A and B that make this statement true will produce an infinite number of solutions. The two equations are the same thing; they differ only in their representation.Therefore, the answer is that we require to multiply the second equation by 1/2 in order to get the first equation. Any value of A and B that make this statement true will produce an infinite number of solutions. Let us first write the two equations that we have been given:2x - 3y = A (Equation 1)4x - 6y = B (Equation 2)
Now, let's analyze these equations one by one and find a way in which they are related to each other. As we can see, the second equation is exactly twice the first equation. Therefore, we can obtain the first equation by multiplying the second equation by 1/2:4x - 6y = B2x - 3y = (1/2)B Therefore, any value of A and B that make this statement true will produce an infinite number of solutions.
To know more about equations visit:
https://brainly.com/question/29657992
#SPJ11
I will give brainliest!!!!
Answer two questions about Equations AAA and BBB:
A.3x-1=7
B.3x=8
1) How can we get Equation BBB from Equation AAA?
Choose 1 answer:
(Choice A)
A
Multiply/divide both sides by the same non-zero constant
(Choice B)
B
Multiply/divide both sides by the same variable expression
(Choice C)
C
Add/subtract the same quantity to/from both sides
(Choice D)
D
Add/subtract a quantity to/from only one side
2) Based on the previous answer, are the equations equivalent? In other words, do they have the same solution?
Choose 1 answer:
(Choice A)
A
Yes
(Choice B)
B
No
Answers
Answer:
1. C
2. A
Step-by-step explanation:
Step 1: Write equation
3x - 1 = 7
3x = 8
Step 2: Use 1st equation and solve
3x = 8
x = 8/3
Step 3: Use 2nd equation and solve
3x = 8
x = 8/3
Both equations have equivalent solutions and the 2nd equation is the simplified version of the 1st.
Ella makes a model of a log cabin that is 8 inches long at a scale of 1/2.5 feet. She makes a second model of the same building at a scale of 1/2.5 feet. How much longer is the second model than the first?
Answers
The second model is 3.2 inches shorter than the first model.
The first model of the log cabin is 8 inches long at a scale of 1/2.5 feet.
To determine the actual length, we need to convert the scale to feet.
1/2.5 feet can be simplified to 2/5 feet. So, the length of the first model in feet is
(8 inches) × (2/5 feet per inch)
= 16/5 feet
= 3.2 feet.
Now, let's calculate the length of the second model. Since it is also at a scale of 1/2.5 feet, the length would be
(1/2.5 feet) × 12 inches
= 4.8 inches.
To find the difference in length between the two models, we subtract the length of the first model from the length of the second model:
(4.8 inches) - (8 inches)
= -3.2 inches.
To learn more about inches follow the link:
https://brainly.com/question/16311877
#SPJ1
Diameter measures from side to side
Radius measures from side to center.
For example, AE is the diameter and AH is the radius.
Here is a circle with center H and some line segments and curves joining points on the circle.
Identify examples of the following. Explain your reasoning.

Answers
The region's sector AHB is a circle's sector. This is due to the fact that it diameter is shaped like a slice of pizza and is bounded by two radii and an arc of the circle.
what is diameter?In geometry, the diameter of a circle is any linear fashion segment that has an endpoint mostly on circle and travels through its centre. Another way to put it is the tallest chord of a circle
The diameter of the circle is represented by the line segment AB. This is due to the fact that it runs through the centre H and connects two points on the circle.
The radius of the circle is represented by the line segment AH. This is because it connects the circle's centre H to a point A.
The chord is the line segment. The chord CD is a circle chord. This is due to the fact that it connects two points on a circle but does not pass through the centre.
Tangent to the circle: The line segment EF is tangent to the circle. This is due to the fact that it only intersects the circle at one point, G, and is perpendicular to the radius GH at that point.
ABG's curve is an arc of the circle. This is because it is part of the circle's circumference, connecting two points A and B.
The region's sector AHB is a circle's sector. This is due to the fact that it is shaped like a slice of pizza and is bounded by two radii and an arc of the circle.
To know more about diameter visit:
https://brainly.com/question/5501950
#SPJ1
find the area of the Polygon
Pls Help!! :)

Answers
One of sides
6cm and 16cm
The other
12cm and 8cm
The area is found by calculating the areas of both and then adding them
Area =Length x Width
Area(1)=6 x 16 = 96 cm squared
Area(2)=12 x 8 = 96 cm squared
Total Area of polygon= Area(2) + Area(2)
=96 + 96
=192 cm squared
Carrie solved = by cross multiplying to get 4x = 6 and then divided both sides by 4. She got x = which reduced to x = . Is there a faster way to solve this problem?
Answers
Answer:
Ok, when we have an equality, like:
A = B
That says that A is the same as B.
Then if a multiply, divide, add or subtract (or do a lot of other operations) in both sides of the equality, the equality does not change.
I suppose that we start with something like:
(4/3)*x = 2
(i will work with this, because you did not post the actual equations)
the thing that Carrie did is:
She multiplies both sides by 3, and get:
3*(4/3)*x = 2*3
4*x = 6
Now she divides bot sides by 4
4*x/4 = 6/4
x = 6/4 = 3/2.
Now, a simpler step is considerin (4/3) as a number A, then we have:
A*x = 2
Now we divide both sides by A.
A*x/A = 2/A
x = 2/A
and we have A = (4/3) then 1/A = (3/4)
x = 2*(3/4) = 3/2
!HELP ASAP / GEOMETRY
15 POINTS
what is the side length?

Answers
Answer:
The length of the side would be 9
Step-by-step explanation:
You can just multiply from the smaller figure 7*3=21, 5*3=15, so then 3*3=9
AABC is dilated by a scale factor of 0.5 with the origin as the center of dilation, resulting in the image AA'B'C'. If A=(2, 2), B=(4, 3), and C= (6,3).
what is the length of B'C' ?
A. 3 units
B. 4 units
C. 2 units
D. 1 unit
Answers
Answer: The length of B'C' is 1 unit
Step-by-step explanation:
To find the length of B'C', we need to find the coordinates of B' and C'. We can do this by applying the dilation transformation to the coordinates of B and C.
If the scale factor is 0.5 and the origin is the center of dilation, then the new coordinates (B' and C') are found by multiplying the original coordinates (B and C) by 0.5.
This means that B' is at (0.5 * 4, 0.5 * 3) = (2, 1.5) and C' is at (0.5 * 6, 0.5 * 3) = (3, 1.5). The length of B'C' is the distance between these two points, which we can find using the distance formula:
distance = sqrt((3 - 2)^2 + (1.5 - 1.5)^2)
= sqrt((1)^2 + (0)^2)
= sqrt(1)
= 1
Therefore, the length of B'C' is 1 unit
(3x³ - 5x² + 16) + (10x³ − 8x + 11)
Answers
10² - (-10)² - (-10)²

Answers
Answer:
-100 (10*10)- (-10*-10) - (10*10)
Step-by-step explanation:
what is the opposite of -89?
Answers
Answer:
89
Step-by-step explanation:
Which is the correct first step in solving the inequality –4(2x – 1) > 5 – 3xanswers are?ADistribute–4 to get –8x + 4 > 5 – 3x.BDistribute –4to get –8x – 1 > 5 – 3x.CSubtract2xfrom both sides of the inequality.DAdd 1to both sides of the inequality
Answers
The correct first step in solving the inequality –4(2x – 1) > 5 – 3x is option A: Distribute –4 to get –8x + 4 > 5 – 3x.
This is because we are trying to solve for x, so we need to get x on one side of the inequality and all the other terms on the other side. In order to do this, we need to apply distributive property of multiplication over addition, which means we need to multiply the -4 with the 2x-1. By doing this we get -8x + 4 > 5 - 3x. This can help us to move forward in solving the inequality. This is the correct first step as it gets us closer to isolating the variable x on one side of the inequality.
After this step, we can further simplify the inequality by adding or subtracting similar terms to get the final solution.
It is important to remember that when solving inequalities we need to be careful with the signs, specially when dividing or multiplying by a negative number, as it might change the direction of the inequality.
To know more about mathematical inequality click below:
https://brainly.com/question/19003099#
#SPJ4