Asha is 4 years less than 3 times the age of her daughter. If the sum of their ages is 48 years. Find their age.
Answers
Answer:
28
Step-by-step explanation:
48/3=16
48-16=32
32-4=28
Related Questions
(08.05 MC)The following box plot shows the number of books sold each day at a bookstore for 40 days. How many days did the bookstore sell 2 to 12 books?

Answers
Answer:
20 days
Step-by-step explanation:
Number of books sold each day for 40 days :
The first quartile (Q1) = 2
For the 25% of the days = 2 books were sold
Hence 0.25 * 40 = 10 days, 2 books or less were sold
The upper quartile (Q3) = 12 books
For up to 75% of the days = 0.75 * 40 = 30 days ; 12 books or less were sold
To obtain the number of books sold between 2 and 12 ; we subtract :
(30 days - 10 days) = 20 days
Answer:
20
Step-by-step explanation:
here is a scatter plot for a set of bivariate data. what would you estimate the correlation coefficient to be?
Answers
You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
What is meant by scatter plot?The relationship between the two variables in a bivariate data set is graphically represented by a scatter plot. Consider them to be the graphic depiction of two data sets that have been combined by allocating each axis in the plot to a distinct variable.
Due to the presence of two variables, this type of data is known as bivariate data. Only 1 variable may be displayed on a line plot. You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
The standard deviation of each variable and the covariance between them must first be determined in order to calculate the Pearson correlation. Covariance is subtracted from the product of the standard deviations of the two variables to get the correlation coefficient.
To learn more about scatter plot refer to:
https://brainly.com/question/6592115
#SPJ4
A woman rides her bike 16 miles with the wind in the same time she travels 10 miles against the wind. If the speed of the wind is 3 mph, find the speed of the cyclist in still air.
Answers
The speed of the cyclist in still air is 13 mph
How to find the speed of the cyclist in still airLet the speed of the cyclist in still air be x mph
when she rides with the wind her speed = (x + 3) mph
when she rides against the wind her speed = (x - 3) mph.
Mathematically we can represent the problem as:
16 / (x + 3) = 10 / (x - 3)
cross multiplying and simplifying
16 (x - 3) = 10 (x + 3)
16x - 48 = 10x + 30
6x = 78
x = 13
Learn more about speed of the wind at
https://brainly.com/question/29801913
#SPJ1
we have a study involving 3 different groups that each contain 9 participants (27 total). what two degrees of freedom would we report when we report the results of our study?
Answers
Using degree of freedom,
Two degrees of freedom would we report when we report the results of our study is (2,24).
Degree of freedom:
The statistical degrees of freedom (DF) indicate the number of independent values that can be changed in the analysis without violating the constraints.
degrees of freedom is the number of independent values that can be estimated in a statistical analysis. It can also be thought of as the number of values that are free to vary when estimating the parameters
DF = N – P
Where:
N = sample size
P = the number of relationships
We given that,
Number of groups , k = 3
Number of total participants, n = 27
Degrees of freedom for F-test is F(k-1,n-k)
= F(3-1 , 27-3)
= F(2,24)
Hence, (2,24,) are required two degrees of freedom.
To learn more about degree of freedom in statistics, refer:
#SPJ4
I need help with this math question please I don’t understand? And also what is this kind of math called ?

Answers
The exact answer please

Answers
Answer:
$36.42 or $36.72
Step-by-step explanation:
different answers depends on order
Use the Simpson's rule to approximate ∫ 2.4 2f(x)dx for the following data
x f(x) f'(x)
2 0.6931 0.5
2.20.7885 0.4545
2.40.8755 0.4167
Answers
To approximate the integral ∫2.4 to 2 f(x) dx using Simpson's rule, we divide the interval [2, 2.4] into subintervals and approximate the integral within each subinterval using quadratic polynomials.
Given the data points (x, f(x)) = (2, 0.6931), (2.2, 0.7885), and (2.4, 0.8755), we can use Simpson's rule to approximate the integral.
Step 1: Determine the step size, h.
Since we have three data points, we can divide the interval [2, 2.4] into two subintervals, giving us a step size of h = (2.4 - 2) / 2 = 0.2.
Step 2: Calculate the approximations within each subinterval.
Using Simpson's rule, the integral within each subinterval is given by:
∫f(x)dx ≈ (h/3) * [f(x₀) + 4f(x₁) + f(x₂)]
where x₀, x₁, and x₂ are the data points within each subinterval.
For the first subinterval [2, 2.2]:
∫f(x)dx ≈ (0.2/3) * [f(2) + 4f(2.1) + f(2.2)]
≈ (0.2/3) * [0.6931 + 4(0.7885) + 0.8755]
For the second subinterval [2.2, 2.4]:
∫f(x)dx ≈ (0.2/3) * [f(2.2) + 4f(2.3) + f(2.4)]
≈ (0.2/3) * [0.7885 + 4(0.4545) + 0.8755]
Step 3: Sum up the approximations.
To obtain the approximation of the total integral, we sum up the approximations within each subinterval.
Approximation ≈ (∫f(x)dx in subinterval 1) + (∫f(x)dx in subinterval 2)
Calculating the values, we get the final approximation of the integral ∫2.4 to 2 f(x) dx using Simpson's rule.
To learn more about Simpson's rule click here:
brainly.com/question/30459578
#SPJ11
Janelle is considering two options for saving money. One option earns simple interest while the other option earns interest compounded monthly. If there are no additional deposits or withdraws, how much more will Janelle earn with the compound interest option? Assume Janelle deposits $3,000 at 3% interest for 7 years for both options
Answers
Janelle will earn approximately 729.19 more with the compound interest option compared to the simple interest option over a period of 7 years.
The amount Janelle will earn with the compound interest option can be calculated using the formula for compound interest:
\(A = P(1 + r/n)^{(nt)}\)
Where:
A is the total amount after interest has been compounded
P is the principal amount (the initial deposit)
r is the annual interest rate (expressed as a decimal)
n is the number of times interest is compounded per year
t is the number of years
In this case, Janelle deposits 3,000 at an interest rate of 3% for 7 years. We'll compare the simple interest and compound interest options.
For the simple interest option, the interest is calculated using the formula:
I = P * r * t
Where:
I is the total interest earned
Using the given values, we can calculate the interest earned with simple interest:
I = 3000 * 0.03 * 7
I = 630
Now, let's calculate the total amount earned with the compound interest option.
Since the interest is compounded monthly, the interest rate needs to be divided by 12 and the number of years needs to be multiplied by 12:
r = 0.03/12
t = 7 * 12
Using these values, we can calculate the total amount with compound interest:
\(A = 3000 * (1 + 0.03/12)^{(7*12)}\)
A ≈ 3,729.19
To find out how much more Janelle will earn with the compound interest option, we subtract the initial deposit from the total amount with compound interest:
Difference = A - P
Difference = 3,729.19 - 3,000
Difference ≈ 729.19
Therefore, Janelle will earn approximately 729.19 more with the compound interest option compared to the simple interest option over a period of 7 years.
Learn more about compound interest visit:
brainly.com/question/14295570
#SPJ11
A rectangle with a perimeter of
48
48 units is the image of a rectangle that was dilated by a scale factor of
3
2
2
3
. Find the perimeter of the preimage, the original rectangle, before its dilation. Round your answer to the nearest tenth, if necessary
Answers
If a rectangle has a perimeter of 48 in. the length and width are scaled by a factor of 2.5, the perimeter of the resulting rectangle is 225 inches.
Here, we have,
Let L be the length of the original rectangle and W be the width.
Then, the perimeter of the original rectangle is P = 2L + 2W = 48 inches.
If we scale the length and width by a factor of 2.5, we get a new length of 2.5L and a new width of 2.5W. The perimeter of the new rectangle would be:
P' = 2(2.5L) + 2(2.5W)
= 5L + 5W
To find the new perimeter, we need to find the new values of L and W. Since the length and width are scaled by the same factor, we can write:
2.5L = kL
2.5W = kW
where k is the scaling factor.
Since the new rectangle is scaled by a factor of 2.5, k = 2.5.
Therefore:
L' = 2.5L = 2.5(12) = 30 inches
W' = 2.5W = 2.5(6) = 15 inches
The new perimeter is:
P' = 5L' + 5W'
= 5(30) + 5(15)
= 225 inches
To learn more about perimeter click on,
brainly.com/question/2855380
#SPJ1
Graph y= 0.5x^2 - 4x +6 on the coordinate plane.
Vertex:
Is this considered a minimum or maximum point?
Axis of symmetry: x=
Roots: x= and x=
Answers
Answer:
V: (4, -2), min, Axis: x = 4, Roots 2 and 6
Step-by-step explanation:
Multiply everything x 2 to get rid of the decimal in front of x^2
2y = x^2 - 8x + 12
Factor
2y = (x - 6)(x - 2)
The roots are at 2 and 6.
The axis of symmetry is in the center between the roots, so it is x = 4.
Put 4 into the original equation to find y
y = 0.5(4*2) - 4(4) + 6
y = 8 - 16 + 6, y = -2
Vertex is at (4, -2). It is a minimum because the graph opens up since x*2 is positive.
What is the average rate of change for the wages earned between 12 and 30 hours
Number of Hours Wages
12 $675.00
15 $843.75
23 $1,293.75
30 $1,687.50
Answers
Answer:
9586
Step-by-step explanation:
Find the length of side x in simplest radical form with a rational denominator.
{DELTA MATH PROBLEM}

Answers
Answer:
x = sqrt (22)
Step-by-step explanation:
This is a RIGHT triangle with the two legs of equal length sqrt 11
us pythagorean theorem
a^2 + b^2 = c ^2 where a and b are the legs and c = hypotenuse
(sqrt11)^2 + (sqrt11)^2 = x^2
11 + 11 = x^2
x = sqrt (22)
Which of the following is an equation of the line through (2, 3) and (-1, -12)?
Answers
Answer:
y = 5x - 7
Step-by-step explanation:
First point coordinates
x₁
2
y₁
3
Second point coordinates
x₂
-1
y₂
-12
Result
Slope (m)
5
m = -15 / -3 = -5 / -1 = 5
Your function
The entered points belong to an increasing, linear function.
Equation: y = 5x - 7.
Hope i helped :)
plssss helppppppp I need a least to greatest

Answers
Answer:
-1/8, 69%, 5 and 50
Step-by-step explanation:
→ Convert -1/8 to a number format
-1/8 = -0.125
→ Convert 69% to a number format
0.69
→ Now place in order
-0.125, 0.69, 5, 50
please put the math too I really need it ;)

Answers
Answer:1) 32. 2). 3) 21. 4) 4
Step-by-step explanation: 1) 4*8=32m, 2) I don't know, 3) 6*7=42 for the area of a square but since a triangle half it so its 21, An the last is by 4 for example 4*10=40 but if doubled its 20*8 and that equals 160. and 160/40=4
The ratio of the width to the length of a rectangle is 3 to 5.
The perimeter of the rectangle is 64 cm.
What are the width and length of the rectangle?
Answers
Step-by-step explanation:
let width= 3x and length = 5x
perimeter = 64cm
now perimeter = 2(length+width)
64= 2(3x+5x)
64 = 16x
x = 4
therefore width= 3 X 4 = 12
length = 5 X 4 = 20
PLEASE HELP ASAP!!!!!!!!!!!!!!!!

Answers
Answer:
25
Step-by-step explanation:
180-130=50
50/2=25
Answer:
x = 25 degrees
Step-by-step explanation:
the figure is an isosceles triangle
x + x + 130 = 180
2x + 130 = 180
2x = 180 - 130
2x = 50
x = 25 degrees
Help me please thank you

Answers
Answer: d. 5/9v -5/9
Step-by-step explanation:
2/9v +1/3v -5/9
2/9v + 3/9v-5/9
5/9v -5/9
Carla paid for an Introduction to Painting course at Color Castle Art Studio. The cost of the course covers 12 painting classes. She also bought a beginner's painting kit for $28. Carla paid $220 in all. How much does each painting class cost?
Answers
Answer:
$16
Steps:
12C + 28 = 220
12C = 220 - 28
12C = 192
C = 192÷12
C = 16
Each painting class costs $16
The cost of each painting class is $16.
Here,
The cost of the course covers 12 painting classes and she also bought a beginner's painting kit for $28.
Carla total paid = $220
We have to find the cost of each painting class.
What is Mathematical system?
The combination of numbers and variables by using operations addition, subtraction, multiplication and division is called Mathematical expression.
Now,
Let the cost of each painting class = $x
And, The cost of the course covers 12 painting classes.
She also bought a beginner's painting kit for $28 and paid $220 in all.
Hence, The equation is;
12x + 28 = 220
12x = 220 - 28
12x = 192
x = 192 ÷ 12
x = 16
Therefore, The cost of each painting class is $16.
Learn more about the mathematical system visit:
https://brainly.com/question/4686750
#SPJ2
math work
pls help
bleh

Answers
Answer:
yes
Step-by-step explanation:
substitute 4 for g. 4x5= 20 and 20 is definitely less than or equal to 25
Answer:
yes
Step-by-step explanation:
Given
5g ≤ 25
If g = 4 then
5g = 5 × 4 = 20 and
20 ≤ 25
Thus g = 4 is a solution of the inequality
complete the ven diagram

Answers
100 participants in a sports facility are polled. The swimming pool and exercise centre are frequently used by 36 people. 57 people utilize the fitness centre. The pool is used by 49 people. The values for the Venn diagram are 70, 21, and 30, respectively.
To identify the sets in this activity, which requires combination knowledge, we can state that:
just 21 fitness70 fitness and swimming, only 13 swimming, and 30 nothing elseWe can infer the following from the text's data:
There are 100 people in total in this sports centre.57 individuals frequent the fitness centre.The pool is routinely used by 49 persons.A total of 36 people frequently use the pool and fitness centre.Hence, those who exclusively practice fitness suites are = 57-36 = 21
Hence, those who solely use a swimming pool are = 49 - 36 = 13
Hence, the overall participation rate in the swimming pool and fitness centre = 21+13+36 = 70
To learn more about the Venn diagram, refer:-
https://brainly.com/question/29301560
SPJ1
Let S be any sample space, and E, F and G be any three events. Describe the event that E and F occur, and G does not occur.
a) ( E ∪ Fc ) ∩ G
b) ( E ∪ F ) ∩ G
c) ( E ∪ F ) ∩ Gc
d) ( E ∩ F ) ∪ Gc
e) E ∩ F ∩ Gc
f) None of the above.
Answers
The event that E and F occur, and G does not occur is E ∩ F ∩ Gc. So, correct option is E.
The event that E and F occur, and G does not occur can be represented by the expression (E ∩ F) ∩ Gc. Let's break down the options provided to determine the correct representation:
a) (E ∪ Fc) ∩ G: This represents the event where either E or the complement of F occurs, and G occurs. It does not capture the condition that both E and F occur.
b) (E ∪ F) ∩ G: This represents the event where either E or F occurs, and G occurs. It does not exclude the possibility of E and F occurring together.
c) (E ∪ F) ∩ Gc: This represents the event where either E or F occurs, and G does not occur. However, it does not specify that E and F occur together.
d) (E ∩ F) ∪ Gc: This represents the event where either E and F occur together or G does not occur. It does not exclude the possibility of E and F occurring without G.
e) E ∩ F ∩ Gc: This correctly represents the event where both E and F occur together, and G does not occur. This is the desired outcome as stated in the question.
Therefore, the correct representation for the event is option e) E ∩ F ∩ Gc.
To learn more about sample space/events click on,
https://brainly.com/question/31974975
#SPJ4
What is the x-coordinate of point B?
A
-1
B
- 4
С
1
D
4

Answers
Answer:
it should be -4 bc the point B goes right above the -4
I don’t know how to do this o need help plz
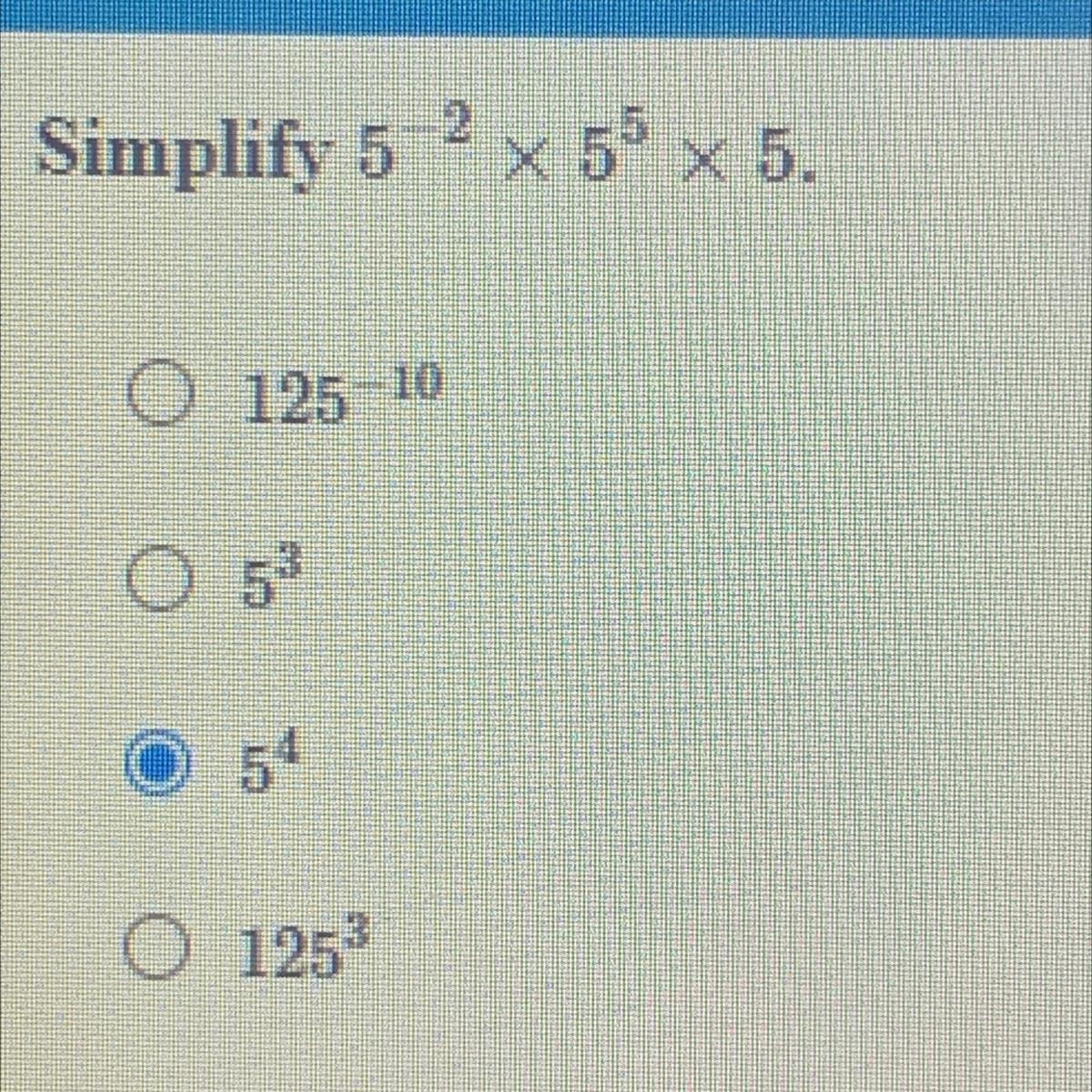
Answers
Explanation: 5^-2 x 5^5 x 5 = 625
5^4 = 625
3. triangle abc has angle measures as shown (look at image).
(a) using the triangle sum theorem, write the equation and solve for x.
(b) what is the value of < b? show your work.

Answers
Answer:
x = 6, ∠B = 50°
Step-by-step explanation:
a) 8x + 2 + 70 + 60 = 180
8x + 132 = 180
8x = 180 - 132 = 48
x = 48/8 = 6
b) ∠B = 180 - 70 - 60 = 50°
or 8x + 2 = 8*6 + 2 = 50°
Which imaginary cardinal plane bisects the body into right and left halves?
A. sagittal
B. frontal
C. transverse
D. none of the above
Answers
The imaginary cardinal plane that bisects the body into the right and left halves is the sagittal plane.
The sagittal plane is a vertical plane that divides the body into left and right halves. It runs parallel to the midline of the body, from front to back. The term "sagittal" comes from the Latin word "sagitta," meaning arrow, referring to the shape of an arrow cutting through the body.
The frontal plane, also known as the coronal plane, divides the body into front (anterior) and back (posterior) halves. It is perpendicular to the sagittal plane and runs from side to side, dividing the body into front and back sections.
The transverse plane, also called the horizontal plane or axial plane, divides the body into upper (superior) and lower (inferior) halves. It is perpendicular to both the sagittal and frontal planes and runs horizontally, dividing the body into top and bottom portions.
Therefore, of the given options, the sagittal plane is the imaginary cardinal plane that bisects the body into the right and left halves.
Visit here to learn more about perpendicular:
brainly.com/question/12746252
#SPJ11
Jacob is cutting yarn for a craft project. He needs pieces of yarn that are 12 inches long, but he only has a ruler marked with centimeters. Luckily, he remembers that there are 2.54 centimeters in an inch. How many centimeters long should Jacob's pieces of yarn be?
Answers
Answer:
30.48 centimeters
Step-by-step explanation:
We know that:
2.54 cm = 1 inch
To find how many centimeters are in 12 inches, you should:
2.54 x 12 = 30.48
So Jacob’s pieces of yarn should be 30.48 centimeters long.
Hope this helps!
Jacob's pieces of yarn should be 30.48 centimeters long.
How to determine How many centimeters long should Jacob's pieces of yarn be?To find out how many centimeters long Jacob's pieces of yarn should be, we can use the conversion factor that there are 2.54 centimeters in an inch.
Since Jacob needs pieces of yarn that are 12 inches long, we can calculate the length in centimeters using the conversion:
Length in centimeters = Length in inches * Conversion factor
Length in centimeters = 12 inches * 2.54 centimeters/inch
Length in centimeters = 30.48 centimeters
So, Jacob's pieces of yarn should be 30.48 centimeters long.
Learn more about centimeters at https://brainly.com/question/18570674
#SPJ3
High-rent district: The mean monthly rent for a one-bedroom apartment without a doorman in Manhattan is S2676. Assume the standard deviation is S509. A real estate firm samples 108 apartments. Use the TI-84 Plus calculator. Part 1 of 5 (a) What is the probability that the sample mean rent is greater than S2746? Round the answer to at least four decimal places The probability that the sample mean rent is greater than S2746 is Part 2 of 5 (b) What is the probability that the sample mean rent is between S2550 and $2555? Round the answer to at least four decimal places. The probability that the sample mean rent is between S2550 and S2555 is Part 3 of 5 (c) Find the 75th percentile of the sample mean. Round the answer to at least two decimal places. The 75th percentile of the sample mean rent is S Part 4 of 5 (d) Would it be unusual if the sample mean were greater than $2780? Round answer to at least four decimal places. (Choose one) ,because the probability that the sample mean is greater than S2780 is Part 5 of 5 (e) Do you think it would be unusual for an individual to have a rent greater than S2780? Explain. Assume the variable is normally distributed. Round the answer to at least four decimal places (Choose one),because the probability that an apartment has a rent greater than $2780 is
Answers
The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Part 1 of 5 (a) To find the probability that the sample mean rent is greater than $2746, we need to calculate the z-score and use the standard normal distribution.
First, we calculate the z-score using the formula:
z = (x - μ) / (σ / sqrt(n))
Where:
x = sample mean rent = $2746
μ = population mean rent = $2676
σ = standard deviation = $509
n = sample size = 108
Plugging in the values, we get:
z = (2746 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 2.3008.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2746 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0107.
Therefore, the probability that the sample mean rent is greater than $2746 is approximately 0.0107.
Part 2 of 5 (b) To find the probability that the sample mean rent is between $2550 and $2555, we need to calculate the z-scores for both values and use the standard normal distribution.
Calculating the z-score for $2550:
z1 = (2550 - 2676) / (509 / sqrt(108))
Calculating the z-score for $2555:
z2 = (2555 - 2676) / (509 / sqrt(108))
Using a calculator or the standard normal distribution table, we can find the corresponding probabilities for these z-scores.
Let's assume we find P(Z < z1) = 0.0250 and P(Z < z2) = 0.0300.
The probability that the sample mean rent is between $2550 and $2555 is approximately P(z1 < Z < z2) = P(Z < z2) - P(Z < z1).
Substituting the values, we get:
P(z1 < Z < z2) = 0.0300 - 0.0250 = 0.0050.
Therefore, the probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
Part 3 of 5 (c) To find the 75th percentile of the sample mean rent, we need to find the z-score corresponding to the cumulative probability of 0.75.
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to a cumulative probability of 0.75. Let's assume this z-score is denoted as Zp.
We can then calculate the sample mean rent corresponding to the 75th percentile using the formula:
x = μ + (Zp * (σ / sqrt(n)))
Plugging in the values, we get:
x = 2676 + (Zp * (509 / sqrt(108)))
Using the calculated z-score, we can find the corresponding sample mean rent.
Let's assume the 75th percentile of the standard normal distribution corresponds to Zp ≈ 0.6745.
Substituting the value, we get:
x = 2676 + (0.6745 * (509 / sqrt(108)))
Calculating this value, we find x ≈ 2702.83.
Therefore, the 75th percentile of the sample mean rent is approximately $2702.83.
Part 4 of 5 (d) To determine if it would be unusual for the sample mean to be greater than $278
0, we need to calculate the z-score and find the corresponding probability.
Calculating the z-score:
z = (2780 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that the sample mean rent is greater than $2780 is approximately 0.0717.
Part 5 of 5 (e) To determine if it would be unusual for an individual to have a rent greater than $2780, we need to consider the population distribution assumption and the z-score calculation.
Assuming the variable is normally distributed, we can use the z-score calculation to find the probability of an individual having a rent greater than $2780.
Using the same z-score calculation as in Part 4, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that an individual has a rent greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that an individual has a rent greater than $2780 is approximately 0.0717.
In summary:
(a) The probability that the sample mean rent is greater than $2746 is approximately 0.0107.
(b) The probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
(c) The 75th percentile of the sample mean rent is approximately $2702.83.
(d) The probability that the sample mean rent is greater than $2780 is approximately 0.0717.
(e) The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
A rectangle has a diagonal of 12 feet and length of 9 feet. What is ghye width of the rectangle, in simplified form? (No decimal Answers (
Answers
The width of the rectangle is;
\(3\sqrt[]{7}\text{ ft}\)Here, we want to get the width of the rectangle
To do this, we need a pictorial representation
We have this as;
As we can see, the rectangle is divided into two equal right-triangles
We have represented the width by w
We can use Pythagoras' theorem to get the width
The square of the diagonal (the hypotenuse) is equal the sum of the squares of the two other sides
Thus, we have;
\(\begin{gathered} 12^2=9^2+w^2 \\ 144=81+w^2 \\ w^2\text{ = 144-81} \\ w^2\text{ = 63} \\ w\text{ = }\sqrt[]{63} \\ w\text{ = 3}\sqrt[]{7}\text{ ft} \end{gathered}\)
For each expression, write an equivalent expression that uses only addition. Do not include any spaces in your answers. Keep the terms in the same order. 20−9+8−7 and 4x−7y−5z+6
Answers
Answer:
(a)\(20+(-9)+8+(-7)\)
(b)\(4x+(-7y)+(-5z)+6\)
Step-by-step explanation:
We are required to write an equivalent expression that uses only addition for each of the given term.
Note that the product of + and - is always -.
Therefore:
(a)20−9+8−7
\(20-9+8-7 \\=20+(-9)+8+(-7)\)
(b)4x−7y−5z+6
\(4x-7y-5z+6\\=4x+(-7y)+(-5z)+6\)