Donald can read 3/4 of a book in 1 1/2 hours.
Answers
Answer:
Thats fun but i want to help! what the question?
Step-by-step explanation:
Related Questions
Six less than 3/4 of a number is the same as the number. Find the number.
Answers
Step-by-step explanation:
0.75x - 6 = x
0.25x = -6
x = -24
Hence the number is -24.
which has greater cenetic energy a car traveling 30.0 km/hr or one twice as heavy traveling at 15 km/hr?
Answers
Answer:
30 km/h car
Step-by-step explanation:
From analysis the car traveling at 30 km/h has greater kinetic energy
we can deduce it from the expression of kinetic energy which is
\(KE=\frac{1}{2} mv^2\)
Assuming the mass m= 1 kg
For the 30 km/h
\(KE=\frac{1}{2}*1*30^2 \\\\KE=\frac{1}{2}*1*900\\\\\KE=450 J\)
For the 15 km/h
\(KE=\frac{1}{2}*2*15^2 \\\\ KE=\frac{1}{2}*2*225 \\\\\ KE=\frac{1}{2}*450 J\\\\\ KE=225 J\)
Though the kinetic energy is a function of mass and velocity, but from our analysis the faster moving object has more KE
23. the difference between the number of customers in line at the express checkout and the number in line at the super-express checkout in exercise 3 is x1 2 x2. calculate the expected difference.
Answers
The expected difference is 0.17
What is super express market?A supermarket is a self-service store with various food, drink, and household goods options divided into categories. While this type of store is bigger and has a wider variety of products than older grocery stores, it is smaller and offers a smaller selection of goods than a hypermarket or big-box market. Fresh meat, produce, dairy, deli foods, baked goods, etc. may usually be found in the store.
Additionally, shelf space is set aside for canned and packaged goods as well as a variety of non-food items like pet supplies, cleaning supplies, cookware, and household cleansers.
The table is: 0 1 2 3
x1 0 0.08 0.06 0.04 0.00
1 0.05 0.18 0.05 0.03
2 0.05 0.04 0.10 0.06
3 0.00 0.03 0.04 0.07
4 0.00 0.01 0.05 0.06
Expected difference =
+(0.08*(0-0)) +(0.06*(0-1)) +(0.04*(0-2)) +(0.00*(0-3)) +(0.05*(1-0)) +(0.18*(1-1)) +(0.05*(1-2)) +(0.03*(1-3)) +(0.05*(2-0)) +(0.04*(2-1)) +(0.10*(2-2)) +(0.06*(2-3)) +(0.00*(3-0)) +(0.03*(3-1)) +(0.04*(3-2)) +(0.07*(3-3)) +(0.00*(4-0)) +(0.01*(4-1)) +(0.05*(4-2)) +(0.06*(4-3))
= 0.17
To know more about super express market please visit:
https://brainly.com/question/22416965
#SPJ4
The table to the right lists probabilities for the corresponding numbers of girls in three births. What is the random variable, what are its possible values, and are its values numerical?
Answers
The true statement is (b) the random variable is x, the possible values are 0 to 3 and the values are numerical
How to determine the true statement?The table is added as an attachment
From the attached image, we have:
Number of girls (x) P(x)
0 0.125
1 0.375
2 0.375
3 0.125
In the above, the random variable is x, while P(x) represents its probabilities.
Also, the possible values are 0 to 3 as shown in the table.
0 to 3 are numerical digits, and the values are numerical
Hence, the true statement is (b)
Read more about random variables at:
https://brainly.com/question/15246027
#SPJ12

HELP QUICK, WILL GIVE BRAINLIST!!!

Answers
Answer:
The flag pole is 12.8 feet tall.
Step-by-step explanation:
doing the second one hold up
Which of the following graphs can be used to find the solution to the system of equations shown below 2x+6y=8 and 3x+9y=4
Answers
Answer:
where are the graphs? I have to see them to give a correct answer
find the value of k if (x-3) is a factor of P(x)=2x3-5x2+3x+k
Answers
Answer:
k = -18
Step-by-step explanation:
If x-3 is a factor, what this means is that if we substitute;
x = 3 into the equation, we should get 0
This is from the factor theorem
Thus ;
P(3) = 0 = 2(3)^3 -5(3)^2 + 3(3) + k
0 = 54 - 45 + 9 + k
k + 18 = 0
k = -18
Emma invested $630 in an account in the year 1997, and the value has been growing exponentially at a constant rate. The value of the account reached $840 in the year 2002. Determine the value of the account, to the nearest dollar, in the year 2005.
Answers

Answer:
$966
Step-by-step explanation:
Given that $630 was invested in 1997
At a constant rate the value grew to $840 in 2002.
This implies that $210 was gotten in 5years:
$(840-630)=$210
and 2002-1997= 5years
therefore, to determine the value of the account in 2005: 2005-1997=8years
$210=5years
$x=8years
CROSS MULTIPLY
5x= 210×8
5x=1680
x=$336
Value of account in 2005 will be: $630+$336=$966
Therefore $966 was made in the next 8years(2005).
7. Find the area of the rhombus. Express
your answer as a mixed number of
square centimeters in simplest form.
3 2/3cm
4½cm
Answers
Step 1
Convert
3 2/3
to an improper fraction.
Step 2
Convert
4 1/2
to an improper fraction.
Step 3
Cancel the common factor of 3.
Step 4
Combine
11 and 3/2
Step 5
Multiply
11
by
3.
The result can be shown in multiple forms.
Exact form: 33/2
Decimal form: 16.5
Mixed Number form: 16 1/2
solve 15 2x = 36. round to the nearest ten-thousandth.
Answers
To solve the equation 15 + 2x = 36, we can start by subtracting 15 from both sides of the equation to get 2x = 21. Then, we can divide both sides by 2 to get x = 10.5. Rounded to the nearest ten-thousandth, the solution is x = 10.5000.
IM TAKING A TEST, HELP!
You work at a department store and make $12 per hour plus 7% commission on all sales. If you work 9 hours and sell $900 on Friday, how much do you make all together? SHOW YOUR WORK(no links)
Answers
Step-by-step explanation:
Multiply 12 and 7 then when you get that answer multiply it with 9 and then add it with 900
anyways my bias is Jisoo
Diseases I and II are prevalent among people in a certain population. It is assumed that 11% of the population will contract disease I sometime during their lifetime, 16% will contract disease II eventually, and 2% will contract both diseases. (a) Find the probability that a randomly chosen person from this population will contract at least one disease. .25 Correct: Your answer is correct. (b) Find the conditional probability that a randomly chosen person from this population will contract both diseases, given that he or she has contracted at least one disease. (Round your answer to four decimal places.)
Answers
Answer:
a) \(P(A \cup B)=0.23\)
b) \(P(X)=0.87\)
Step-by-step explanation:
From the question we are told that:
Probability of contacting disease 1 \(P(1)=0.11\)
Probability of contacting disease 2 \(P(2)=0.16\)
Probability of contacting both disease \(P(1\& 2)=0.2\)
a)
Generally the equation for a Random contact is mathematically given by
\(P(A \cup B)=P(1)+P(2)-P(A \cap B)\)
\(P(A \cup B)=\frac{11}{100}+\frac{16}{100}-\frac{4}{100}\)
\(P(A \cup B)=\frac{11+16-4}{100}\)
\(P(A \cup B)=0.23\)
b)
Generally the equation for Probability of contacting both after having contacted one is mathematically given by
\(P(X)=\frac{P(1\& 2)}{P(A \cup B)}\)
Therefore
\(P(X)=\frac{0.2}{0.23}\)
\(P(X)=0.87\)
help me the pic is the queston

Answers
The graph below shows the number of calories burned when someone rides a bicycle.
At what rate are calories burned by bike riding?
Responses

Answers
The rate at which calories are burned was gotten by finding the slope of the graph which gives; 4 calories per minute
How to find the slope of the Linear Graph?
To get the slope of a linear graph, we will take two coordinates and make use of the formula;
Slope = (y₂ - y₁)/(x₂ - x₁)
The two coordinates we will pick for this slope are;
(10, 40) and (20, 80)
Thus;
Slope = (80 - 40)/(20 - 10)
Slope = 40/10
Slope = 4
Since the y-axis represents calories burned and the x-axis represents minutes of exercise, then we can say that;
Rate at which calories get burned by bike riding = 4 calories per minute
Read more about Slope of Linear Graph at; https://brainly.com/question/19376563
#SPJ1
Determine if triangle RST and triangle UVW are or are not similar, and, if they are, state how you know. (Note that figures are NOT necessarily drawn to scale.)
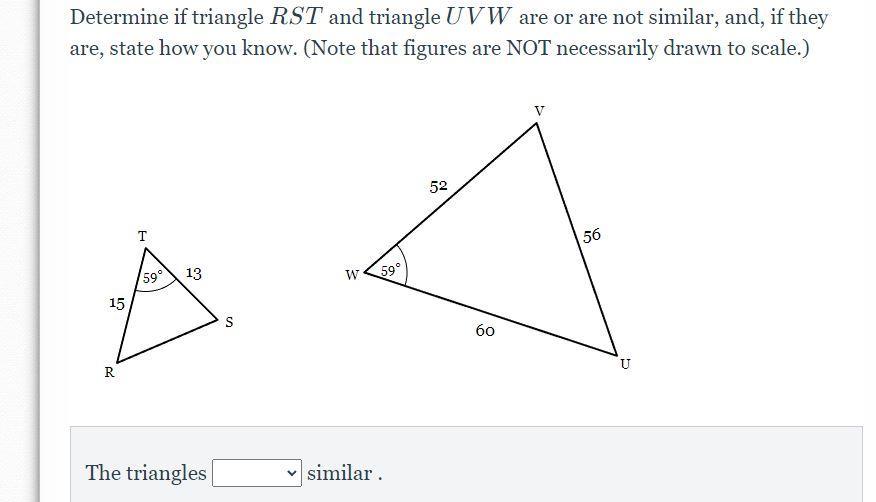
Answers
Yes, the triangles RST and UVW are similar, by SAS similarity rule.
What is similarity?Two similar shapes, such as similar triangles, similar rectangles, similar square, are the shapes whose dimensions are in equal or common ratio but the size or length of their sides vary.
Given that, two triangles RST and UVW,
TR / WU = 15/60 = 1/4
TS / VW = 13/52 = 1/4
∠ T = ∠ W
We know that, if in two triangles their corresponding sides are in equal ratios and have an angle congruent, then they are similar by SAS rule.
Hence, the triangles RST and UVW are similar, by SAS similarity rule.
Learn more about similarity, click;
https://brainly.com/question/26451866
#SPJ1
Dwayne wants to redecorate his bedroom and decides to purchase new furniture. The following graph could be used to represent the value of the new bedroom furniture, f(x), after x years.
a graph of an exponential function which decreases through the points 0 comma 1100 and 2 comma 704
Which of the following statements is/are true based on the graph and the context of the problem?
The function is positive on its entire domain.
The domain is x ≥ 0 to represent the number of years after the bedroom furniture was purchased.
The x-intercept (0, 1100) represents the initial cost of the bedroom furniture.
I only
I and II only
I and III only
I, II, and III
Answers
The correct statements regarding the function are:
I and II only.
What are the correct statements regarding the function?The functions models the value of the furniture after x years, showing exponential decrease. We have that:
Time is never negative, hence the domain is x ≥ 0, representing the number of years since the furniture was purchases.The value of a product will never be negative, and a exponential function that is not shifted never touches 0, hence the function is positive on the entire domain.(0,1100) is the y-intercept, not the x-intercept, and represents the initial cost of the bedroom furniture.Hence statements I and II are correct.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
Answer:
l and lll only
Step-by-step explanation:
just did it
I can wash a car in 20 minutes.how long will it take me to wash 20 cars 10 minutes
Answers
Answer:
It would take 200 minutes
Step-by-step explanation:
2/3 divided by 1 3/7
Answers
Answer:0.46
Step-by-step explanation:
Use the results from the simulation to predict the number of times a
card with the number 10 would be drawn when the total number of
cards drawn in the simulation is 1,440.
Answers
The number of times a card with the number 10 would be drawn when the total number ofcards drawn in the simulation is 1,440 will be 240 tines.
How to illustrate the probability?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1.
In thi situation, the simulation shows that the number of times 10 is drawn is 1/6. The number of times a card with the number 10 would be drawn when the total number ofcards drawn in the simulation is 1,440 will be:
= 1/6 × 1440
= 240 times.
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
Complete question
The simulation shows that the number of times 10 is drawn is 1/6. Use the simulation to predict the number of times a card with the number 10 would be drawn when the total number ofcards drawn in the simulation is 1,440.
A bouncy ball is dropped such that the height of its first bounce is 3.25 feet and each successive bounce is 74% of the previous bounce's height. Write a recursive formula to represent the height of the nth bounce of the ball.
Answers
A recursive formula to represent the height of the nth bounce of the ball is: aₙ = 3.25(0.74ⁿ ⁻ ¹)
How to write a recursive formula?A geometric sequence is a sequence in which the result of the division of consecutive terms is always the same, called common ratio q.
The nth term of a geometric sequence is given by:
aₙ = a(qⁿ⁻¹)
where:
a is the first term
In this problem, the first bounce is 3.25 feet and each successive bounce is 74% of the previous bounce's height, hence the first term and the common ratio are given, respectively, by:
a = 3.25
q = 74% = 0.74
Hence, the height of the nth bounce is given by:
aₙ = 3.25(0.74ⁿ ⁻ ¹)
Read more about Recursive Formula at: https://brainly.com/question/1275192
#SPJ1
pls answer asap with solution, ty

Answers
Answer:
Answer: \(\frac{12}{5}\)
Step-by-step explanation:
\(\frac{3 *4x}{5x-20} \\----x^2-2x----X^2-6x+8\)
\(=\frac{3 * 4x(x^2-6x+8)}{(5x-20)(x^2-2x)} = \frac{12}{5}\)
hope it helped !!
☘☘☘...

Pls help I keep asking and nobody’s helping me

Answers
Answer: 268
Step-by-step explanation: substitute pi with 3.14, & then 4^3 as 64 in the second line. after, you multiply 3.14 x 64 you get 201 after you round. finally multiply 4 x 201 then divide your answer by 3. you get 268. (no one helped so i did)
Find the midpoint of the line segment whose endpoints are (-2, 5) and (6, -9).
(2, -2)
(1, -4)
(4, -4)
Answers
Answer:
The midpoint of the line segment whose endpoints are (-2, 5) and (6, -9) is: (2,-2)
Step-by-step explanation:
Given two points are:
(-2, 5) and (6, -9)
The mid-point is the point that divides a line segment in two equal parts.
Let M be the mid-point then
\(M(x,y) = (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\)
Let
(x1,y1) = (-2, 5)
(x2,y2) = (6, -9)
Putting the values in the formula, we get
\(M(x,y) = (\frac{-2+6}{2}, \frac{5-9}{2})\\M(x,y) = (\frac{4}{2}, \frac{-4}{2})\\= (2,-2)\)
Hence,
The midpoint of the line segment whose endpoints are (-2, 5) and (6, -9) is: (2,-2)
a store prints a request on each receipt asking customers to fill out a satisfaction survey online if they are willing. what type of sample is this?
Answers
The type of sample that a store prints a request on each receipt asking customers to fill out a satisfaction survey online if they are willing is a voluntary response sample.
In the statistics world, a voluntary response sample is a research sample that relies on individual self-selection. This is in opposition to random sampling, in which the samples are gathered in a way that ensures everyone in a particular population has an equal chance of being chosen. This method of self-selection is also known as self-selection bias or sampling bias.Voluntary response samples are subject to a variety of flaws. The responses may not be representative of the population as a whole, and they may be skewed by numerous factors, such as which individuals are most likely to volunteer, how these volunteers differ from the population as a whole, and how the survey questions are phrased.The results of a voluntary response survey may be useful in generating hypotheses or gaining a general sense of how individuals feel about a particular subject. However, they are not reliable enough to draw any conclusions or to be taken seriously in the scientific sense.
To know more about sample refer here:
https://brainly.com/question/13287171
#SPJ11
An independent set in a graph is a set of vertices S⊆V that contains no edge (so no pair of neighboring vertices is included). The max independent set problem is to find an independent set of maximum size in a graph G. (a) Write the max independent set problem as an integer linear program. (b) Write an LP relaxation for the max independent set problem. (c) Construct an example (a family of graphs) to show that the ratio LP-OPT / OPT can be at least cn where c>0 is some absolute constant and n is the number of vertices of the graph. (d) What is the (exact) relation between the size of a max independent set and the size of min vertex cover of a graph? (e) Using this relation, what does the 2-approximation algorithm for vertex cover imply for an approximation algorithm for max independent set?
Answers
The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.
The solution for this question is discussed below:
a) The integer linear program for the max independent set problem is as follows:
maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.
b) The LP relaxation for the max independent set problem is as follows:
Maximize ∑x_iSubject to:
xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.
c) The family of graphs is as follows:
Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.
d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.
e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.
To know more about the independent set, visit:
brainly.com/question/31418821
#SPJ11
I can use your help please

Answers
Answer:
he needs to play 24 games of basketball
Which of the following is a right Riemann sum for arctan(1 + xdx? k=1 © ( aretan (1 + 4) :) į (aretan (4+4) ) ©Ë (arctan ( 1 + **) :) © (aretan (2 + %). :) arctan 1+ .
Answers
The right Riemann sum for arctan(1 + xdx) is Σ[arctan(1 + iΔx)]Δx, where i ranges from 1 to n and Δx is the width of each subinterval. The correct answer among the options provided is (arctan(1 + Δx) + arctan(1 + 2Δx) + ... + arctan(1 + nΔx))Δx.
In a right Riemann sum, the function is evaluated at the right endpoint of each subinterval. Therefore, we add up the values of arctan(1 + iΔx) at the endpoints of the subintervals, where i ranges from 1 to n. The width of each subinterval is Δx, so we multiply the sum by Δx to get the approximate value of the integral.
The provided expression (arctan(1 + Δx) + arctan(1 + 2Δx) + ... + arctan(1 + nΔx))Δx satisfies the conditions of a right Riemann sum, where the function is evaluated at the right endpoint of each subinterval. Therefore, this is the correct option among the given choices.
Learn more about Riemann sum here
https://brainly.com/question/14418174
#SPJ11
A baker can bake 72 muffins in 3 hours. If the baker sell each muffin for $0.85 each, how much money can the baker make?
Answers
He will make $61.20 for 72 muffins in three hours.
Consider the following function. f(x) = -7x3 + 21x + 8 (a) Find the critical numbers of F. (Enter your answers as a comma-separated list.) (b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an answer does not exist, enter DNE increasing decreasing (c) Apply the First Derivative Test to identify the relative ext/emum. (If an answer does not exist, enter DNE.) relative maximum (x, ) = relative minimum (x,y) -
Answers
(a) The critical numbers are x = -1 and x = 1.
(b) The open intervals on which the function is increasing are (-1, 1), and the open intervals on which the function is decreasing are (-inf, -1) and (1, inf).
(c) The relative extrema are: relative maximum (1, 22) and relative minimum (-1, -20).
(a) To find the critical numbers of the function f(x) = -7x^3 + 21x + 8, we first find its derivative:
f'(x) = -21x^2 + 21
Now we set f'(x) = 0 and solve for x:
-21x^2 + 21 = 0
x^2 = 1
x = ±1
The critical numbers are -1 and 1.
(b) To determine the intervals of increasing or decreasing, we evaluate the derivative at points in each interval:
For x < -1: f'(-2) = -21(-2)^2 + 21 = -63 < 0, so the function is decreasing in the interval (-∞, -1).
For -1 < x < 1: f'(0) = 21 > 0, so the function is increasing in the interval (-1, 1).
For x > 1: f'(2) = -21(2)^2 + 21 = -63 < 0, so the function is decreasing in the interval (1, ∞).
(c) Now, we apply the First Derivative Test to the critical numbers:
At x = -1, the function changes from decreasing to increasing, so we have a relative minimum: f(-1) = -7(-1)^3 + 21(-1) + 8 = 14. The relative minimum is (-1, 14).
At x = 1, the function changes from increasing to decreasing, so we have a relative maximum: f(1) = -7(1)^3 + 21(1) + 8 = 22. The relative maximum is (1, 22).
To learn more about function visit;
brainly.com/question/12431044
#SPJ11
A regular hexagon is divided into 6 congruent triangles. If the perimeter of the hexagon. is 48 centimeters, what is the height of each triangle?
A 4 \mathrm{~cm}
B 4 \sqrt{3} \mathrm{~cm}
C 6 \sqrt{3} \mathrm{~cm}
D 8 \mathrm{~cm}
E 8 \sqrt{3} \mathrm{~cm}
Answers
Answer:Your answer would be E
Step-by-step explanation:8 times 6 would be 48
The measure of height of each triangle will be 4√3 cm. Then the correct option is B.
What is the perimeter of the regular polygon?All the sides of the regular polygon are congruent to each other. The perimeter of the regular polygon of n sides will be the product of the number of the side and the side length of the regular polygon.
P = (Side length) x n
A regular hexagon is divided into 6 congruent triangles. If the perimeter of the hexagon is 48 centimeters.
Then the Side length of each triangle will be given as,
48 = (Side length) x 6
Side length = 8 cm
Then the measure of the height of each triangle will be calculated as,
tan 60° = h / (8 / 2)
√3 = h / 4
h = 4√3 cm
The measure of height of each triangle will be 4√3 cm. Then the correct option is B.
More about the perimeter of the regular polygon link is given below.
https://brainly.com/question/10885363
#SPJ2