Check all of the polynomial functions that have 2 as a root.
h(m) = 8 – m3
f(g) = g3 – 2g2 + g
f(a) = a3 – 4a2 + a + 6
f(x) = x3 – x2 – 4
Answers
Answer:
Explained below
Step-by-step explanation:
Polynomial Roots
If x=a is a root of f(x), then f(a)=0
We will test the following functions to check if a=2 is a root.
\(h(m)=8-m^3\)\(h(2)=8-2^3=8-8=0\)
Thus m=2 is a root of h
\(f(g)=g^3-2g^2+g\)\(f(2)=2^3-2\cdot 2^2+2\)
\(f(2)=8-2\cdot 4+2=8-8+2=2\)
Thus g=2 is not a root of f
\(f(a) = a^3 - 4a^2 + a + 6\)\(f(2) = 2^3 - 4\cdot 2^2 + 2 + 6\)
\(f(2) = 8-16+8=0\)
Thus a=2 is a root of f
\(f(x) = x^3 - x^2 - 4\)\(f(2)=2^3 - 2^2 - 4\)
\(f(2)=8 - 4 - 4=0\)
Thus x=2 is a root of f
Answer:
answers are A, C, and D
Step-by-step explanation:
THIS IS CORRECT
Related Questions
Which number can each term of the equation be multiplied by to eliminate the fractions before solving?
6-3/4x+1/3=1/2x+5
Answers
Answer: 12
Step-by-step explanation:
You can multiply by 12 because to get rid of the fractions all terms should be divided by the LCM (ie the smallest multiple that is exactly divisible by 2, 4 and 3)
Multiples of 3 = 3, 6, 9, 12
Multiples of 4 = 4, 8, 12, 16
Multiples of 2 = 2, 4, 6, 8, 10, 12
Therefore the fractions should be multiplied by 12
8.74 + 10.36
If you answer this can you show the work
Answers
Answer:
1 1 (carry the ones)
10.36
8.74
1 9 . 1 0
Step-by-step explanation:
19.10
hope this helps :)
A tree grows three-fourth feet per year. How long will it take the tree to grow from
a height of 17 3/4 feet to a height of 25 1/2 feet?
Answers
Answer:
9 years
Step-by-step explanation:
37-21.25 =15.75ft
1.75ft per year
15.75 / 1.75 = 9 years
how many years after the 1972 ban did it take for ddt levels to move from a rapid to slower rate of decline
Answers
According to all Reports of U.S media and other,
approx. 97 years after in 1972 ban did it take for ddt levels to move from a rapid to slower rate of decline.
DDT (dichloro-diphenyl-trichloroethane) has been one of the most commonly used pesticide chemicals in the United States for many years and was first synthesized in 1874. However, its efficacy as an insecticide was not discovered until 1939. Shortly thereafter, especially during World War I, the United States began producing large amounts of DDT abroad to combat vector-borne diseases such as typhoid fever and malaria. It declined sharply, falling from a peak of about $80m that year to just under $12m in the early 1970s. Over 80% of the amount of pesticides used between 1970 and 1972 was on cotton, with the rest mainly on peanuts and soybeans. The decline in DDT use is due to
(1) increased resistance to insects
(2) development of more effective alternative pesticides
(3) Growing public concern about adverse environmental impacts.
(4) Strengthening government restrictions on the use of DDT.
Residues of the pesticide DDT in the food supply, human tissues, and the environment have declined in recent years, especially since the EPA banned the chemical from major uses in 1972.
To learn more about DDT , refer:
https://brainly.com/question/26747613
#SPJ4
ОЧЕНЬ СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА
на основании какого
свойства равнобедренного треугольника можно доказать медиана равнобедренного треугольника проведенная к его основанию принадлежит серединному перпендикуляру основания
Answers
Если высота, полученная из вершины A, также является медианной, треугольник будет равнобедренным, так что AB = AC, а BC - основание. Следовательно, эта высота также является биссектрисой угла. - Если медиана, проведенная из вершины A, также является биссектрисой угла, треугольник будет равнобедренным, так что AB = AC, а BC - основание.
9/-10 = x/15
What's the right answer?
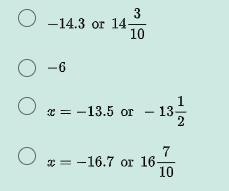
Answers
Step-by-step explanation:
mark me as brilliant plzz

If 22% of a rope is 55 metres long, find the full length
of the rope
Solution
Answers
Answer:
250
Step-by-step explanation:
Let the rope be x meters long
22% of the rope is 55 meters
x *22% = 55
Change to decimal form
x * .22 = 55
Divide each side by .22
x * .22 /.22 = 55/.22
x =250
one hundred twenty-three and thirty hundreths. in decimal form
Answers
Answer:
0.2330
Step-by-step explanation:
if the probability of rain on any given day is 50\%, what is the probability that it will rain on at least three days in a row during a five-day period?
Answers
the probability that it will rain on at least three days in a row during a five-day period is 0.3125.
There are only 2 possibilities for each day that is
1) Raining
2) Not raining
Now, the span of 5 day period is given.
So, the total number of ways will be:
n(S) = 2⁵ = 32
Now, we want probability of rain on exactly 3 days.
We will use combination for the same.
Number of ways = ⁵C₃
= n(A)
= 10
Probability will be:
P = 10 / 32
= 5 / 16
=0.3125
Therefore, the probability that it will rain on at least three days in a row during a five-day period is 0.3125.
Learn more about probability here:
https://brainly.com/question/25870256
#SPJ4
The sum of 10 consecutive integersstarting with 11, equals the sum of 5 consecutive integers, starting with
(A) 22
(B) 29
(C) 31
(D) 33
Answers
Answer: \(\large\boxed{29}\)
Step-by-step explanation:
The sum of 10 consecutive integersstarting with 11
= 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 = 155
Lets try 29:
29 + 30 + 31 + 32 + 33 = 155
Therefore our answer is:
\(\large\boxed{29}\)
in a test of hypothesis the p-value was 0.24 . if the level of significance is 10 % . what is the potential type of statistical error ?
Answers
If the level of significance is 10 %, then the potential type of statistical error is type II error.
What is statical error?
The term "error" (also known as "statistical error") refers to the discrepancy between a value obtained through a data gathering procedure and the population's "actual" value. The data are less representative of the population the higher the inaccuracy.
In the given test,
The p-value = 0.24
Level of significance (a) = 0.10
Here,
0.24 > 0.10
P-value > level of significance
Therefore, We failed to reject the null hypothesis that is actually false
This is type II error,
The type II error occurs when one fails to reject a null hypothesis that is actually false itself.
To know more about statical error, go to link
https://brainly.com/question/28008941
#SPJ4
2x^3y + 18xy - 10x^2y - 90y
Part A: rewrite the expression so that the GCF is factored completely
Part B: rewrite the expression completely factored. Show the steps of your work
___________________________
Part A: the area of a square is (9x^2 + 24x + 16) square units. Determine the length of each side of the square by factoring the area expression completely. Show your work.
Part B: the area of a rectangle is (16x^2 - 25y^2) square units. Determine the dimensions of the rectangle by factoring the area expression completely. Show your work.
___________________________
f(x) = 2x^2 - 5x + 3
Part A: what are the x-intercepts of the graph of f(x)? Show your work
Part B: is the vertex of the graph of f(x) going to be a maximum or minimum? What are the coordinates of the vertex? Justify your answer and show your work.
Part C: what are the steps you would use to graph f(x)? Justify that you can use the answer in part A and part B to draw the graph.
Answers
The expression where the greatest common factor (GCF) is factored completely is \(2x^3y + 18xy - 10x^2y - 90y = 2y(x^3 + 9x - 5x^2 - 45)\)
The expression completely factored in is
\(2y(x^3 + 9x - 5x^2 - 45) = 2y[x(x^2 - 5) + 9(x^2 - 5)]\\= 2y(x - 5)(x^2 + 9)\)
Please refer below for the remaining answers.
We have,
Part A:
To rewrite the expression 2x³y + 18xy - 10x²y - 90y so that the greatest common factor (GCF) is factored completely, we can factor out the common terms.
GCF: 2y
\(2x^3y + 18xy - 10x^2y - 90y = 2y(x^3 + 9x - 5x^2 - 45)\)
Part B:
To completely factor the expression, we can further factor the quadratic term.
\(2y(x^3 + 9x - 5x^2 - 45) = 2y[x(x^2 - 5) + 9(x^2 - 5)]\\= 2y(x - 5)(x^2 + 9)\)
Now,
Part A:
To determine the length of each side of the square given the area expression (9x² + 24x + 16), we need to factor it completely.
The area expression (9x² + 24x + 16) can be factored as (3x + 4)(3x + 4) or (3x + 4)².
Therefore, the length of each side of the square is 3x + 4.
Part B:
To determine the dimensions of the rectangle given the area expression (16x² - 25y²), we need to factor it completely.
The area expression (16x² - 25y²) is a difference of squares and can be factored as (4x - 5y)(4x + 5y).
Therefore, the dimensions of the rectangle are (4x - 5y) and (4x + 5y).
Now,
f(x) = 2x² - 5x + 3
Part A:
To find the x-intercepts of the graph of f(x), we set f(x) equal to zero and solve for x.
2x² - 5x + 3 = 0
The quadratic equation can be factored as (2x - 1)(x - 3) = 0.
Setting each factor equal to zero:
2x - 1 = 0 --> x = 1/2
x - 3 = 0 --> x = 3
Therefore, the x-intercepts of the graph of f(x) are x = 1/2 and x = 3.
Part B:
To determine if the vertex of the graph of f(x) is maximum or minimum, we can examine the coefficient of the x^2 term.
The coefficient of the x² term in f(x) is positive (2x²), indicating that the parabola opens upward and the vertex is a minimum.
To find the coordinates of the vertex, we can use the formula x = -b / (2a), where a and b are the coefficients of the quadratic equation.
For f(x),
a = 2 and b = -5.
x = -(-5) / (2 x 2) = 5/4
To find the corresponding y-coordinate, we substitute this x-value back into the equation f(x):
f(5/4) = 25/8 - 25/4 + 3 = 25/8 - 50/8 + 24/8 = -1/8
Therefore, the vertex of the graph of f(x) is at the coordinates (5/4, -1/8), and it is a minimum point.
Part C:
To graph f(x), we can start by plotting the x-intercepts, which we found to be x = 1/2 and x = 3.
These points represent where the graph intersects the x-axis.
Next,
We can plot the vertex at (5/4, -1/8), which represents the minimum point of the graph.
Since the coefficient of the x² term is positive, the parabola opens upward.
We can use the vertex and the symmetry of the parabola to draw the rest of the graph.
The parabola will be symmetric with respect to the line x = 5/4.
We can also plot additional points by substituting other x-values into the equation f(x) = 2x² - 5x + 3.
By connecting the plotted points, we can draw the graph of f(x).
The steps to graph f(x) involve plotting the x-intercepts, the vertex, and additional points, and then connecting them to form the parabolic curve.
The answer in part A (x-intercepts) and part B (vertex) are crucial in determining these key points on the graph.
Thus,
The expression where the greatest common factor (GCF) is factored completely is \(2x^3y + 18xy - 10x^2y - 90y = 2y(x^3 + 9x - 5x^2 - 45)\)
The expression completely factored in is
\(2y(x^3 + 9x - 5x^2 - 45) = 2y[x(x^2 - 5) + 9(x^2 - 5)]\\= 2y(x - 5)(x^2 + 9)\)
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
20 POINTS!!!!!! HELP PLEASE!!!!!!!


Answers
Answer:
umm???????????? let me try doin it
A must-have for any thrill seeker is a drop tower ride. The Precipice Plummet will stand 420 feet tall. The scale in your architectural diagrams is 1":40'. How tall will your drawing of Precipice Plummet be in inches? (do not include units in your answer, just the number
Answers
The answer is 10.5, but don't put 10.5 if it's just asking for the number and not the unit only put (10)!!!
the shorter diagonal of a rhombus with 70 degrees is 122 cm long, how long is the longer diagonal
Answers
The length longer diagonal is 174 cm.
In a rhombus, the diagonals bisect each other as well as the the vertex angles and adjacent angles are supplementary
So assuming that the 70 degree angle is opposite the 122 cm diagonal, we have
(1/2 length of the shorter diagonal) / sin (35) = (1/2 length of the longer diagonal) / sin(55)
Multiply both sides by 2
( length of the shorter diagonal) / sin (35) = ( length of the longer diagonal) / sin(55)
Multiply both sides by sin(55).
Length of the longer diagonal = sin (55) (122 cm) / sin (35) = 174 cm
Therefore, the length of the longer diagonal is 174 cm.
Learn more about diagonal of a rhombus here:
https://brainly.com/question/4768783
#SPJ12
Solve the following proportions

Answers
Cross multiply
40.3m = 6.5 x 12.4
40.3m = 80.6
Divide through by 40.3
m = 80.6/40.3
m= 2
m= 2
Answer:
\(6.5 \times 12.4 = 40.3 \: m \\ \frac{80.6}{40.3} = 2\)
what is the slope of the line shown below?

Answers
Answer:
A
Step-by-step explanation:
m = (-7 - 6 ) / (-5 - 1)
m = -13 / -6
m = 13/6
How do you solve quotients step by step?
Answers
We can Long Division method to solve quotients step by step
What is long division method and its steps ?
When splitting huge numbers, the task is divided into several sequential parts using the long division approach. The dividend is divided by the divisor, just as in conventional division problems, and the result is known as the quotient; occasionally, it also produces a remainder.
We need to comprehend a few stages in order to divide. A vinculum or right parenthesis separates the dividend from the quotient, while a vertical bar separates the divisor from the dividend. Let's now go through the long division stages listed below to comprehend the procedure.
1. Take the dividend's first digit starting from the left . Verify if this digit exceeds or is equal to the divisor.
2. Next, divide it by the divisor, and write the result as the quotient on top.
3. Subtract the outcome from the digit, and then put the difference below.
Step 4: Decrease the dividend's subsequent digit (if present).
Step 5: Carry out Step 4 again.
Learn more about Long division from the link below
https://brainly.com/question/28824872
#SPJ4
If it takes 5 hours at a speed of 80 km/h to drive a fixed distance, what speed is required to do the same trip in 4 hours?
Answers
Answer:
100 km/h
Step-by-step explanation:
Distance = Speed * Time
Let x be the distance:
x = 80 * 5
x = 400 km
400 / 4 = 100 km/h
Please mark as brainliest
Please help me with this it's algebra WILL GIVE BRAINLIEST and 5 points

Answers
which is right?????

Answers
Answer:
C
Step-by-step explanation:
When talking about multiplication two negatives do, in fact, make a positive but if there is only one negative in the equation, the product(answer) will be negative. Therefore, C 31(-10)=-310 is the only problem that is correct.
Answer:
C.\(31\left(-10\right)=-310\)
Step-by-step explanation:
\(31\left(-10\right)\)
\(\mathrm{Remove\:parentheses}:\quad \left(-a\right)=-a\)
\(=-31\cdot \:10\)
\(\mathrm{Multiply\:the\:numbers:}\:31\cdot \:10=310\)
\(=-310\)
Find the P-value for the test value.
t = 1.619, n = 23, right-tailed
0.0299
0.1196
0.0598
0.0704
Answers
The P-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed value, assuming the null hypothesis is true.
In this case, the null hypothesis is not provided, so we cannot determine the exact P-value.
However, we can use the t-distribution table or a calculator to estimate the P-value for a one-sample t-test with a sample size of 23 and a right-tailed alternative hypothesis.
Using a t-distribution table with 22 degrees of freedom (n-1), we find that the t-critical value for a 0.05 level of significance (alpha) is 1.717. Since the observed t-value of 1.619 is less than the critical value, we can conclude that the P-value is greater than 0.05.
Using a calculator or software, we can obtain a more accurate estimate of the P-value. For a one-sample t-test with the given parameters, the P-value is approximately 0.1196. This means that if the null hypothesis is true, we would expect to obtain a t-value as extreme or more extreme than 1.619 in about 11.96% of all possible samples of size 23.
Therefore, the answer is 0.1196.
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ11
can someone help me do this

Answers
Answer:
False.
Step-by-step explanation:
The ratio is 1:500, which means that the model will be 500 times smaller than the real deal.
The real airplane is 50 metres, or 5,000 centimetres. The model is 50 cm. 5,000 / 50 = 1,000 / 10 = 100 / 1 = 100. Since 100 is NOT equal to 500, the answer is false.
Hope this helps!
An artist is going to cut four similar right triangles from a rectangular piece of paper like the one shown to the right. What is BE to the nearest tenth when AC=13

Answers
The measurement of altitude BE is 4 unit.
What is an altitude?As the average level of the sea's surface, sea level is used to measure altitude. A high altitude is defined as being significantly higher than sea level, such as Mount Everest. It is referred to as having a low altitude when something is closer to the ground, like a plane coming in to land.
As ABCD is rectangle
AD = BC = 12
ΔABC = ΔBCD
BE = FD
5² = 3²+BE²
AE = 3
BE = √(5²-3²)
BE = 4
Thus, The measurement of altitude BE is 4 unit.
To learn mote about altitude refer to :
https://brainly.com/question/18530806
#SPJ1
If f (x) = and g(x) = x − 3, what is the value of g(f (8))?
Answers
Answer:
This is a random thing but is it -24
Step-by-step explanation:
find the value of x

Answers
Answer:
x = 68°
Step-by-step explanation:
∠ DCB = ∠ EDC = 27° ( alternate angles )
Thus ∠ ECB = 23° + 27° = 50°
The sum of the 3 angles in a triangle = 180°, thus
x = 180° - (62 + 50)° = 180° - 112° = 68°
Answer:
68°
Step-by-step explanation:
DE ║ BC
So, ∠DBC = ∠ADE = 62° (∵ Corresponding Angles are equal )
In triangle DEC ,
∠EDC+ ∠ECD = ∠AED (∵ Exterior Angle Sum Property of a triangle )
⇒ ∠AED = 23° + 27° = 50°
Now in triangle AED ,
∠EAD + ∠ADE + ∠AED = 180°
⇒ x° + 62° + 50° = 180°
⇒x° = 180° - 112° = 68°
8|8 Homework: Hw 6.2 For the function z = -8 11 -8x³-5y²2-5xy, find Question Viewer dz dz d dx dy x 2(5,-5), and Question 1, 6.2.3 Part 1 of 4 ayz(5,-5). ****
Answers
To find the partial derivatives of the function z = -8x³ - 5y² + 2xy, we calculate dz/dx, dz/dy, dz/dx(5, -5), and dz/dy(5, -5). We also need to determine the value of ayz(5, -5) for question 6.2.3, part 1 of 4.
To find dz/dx, we differentiate the function z = -8x³ - 5y² + 2xy with respect to x while treating y as a constant. The derivative of -8x³ with respect to x is -24x², and the derivative of 2xy with respect to x is 2y. Thus, dz/dx = -24x² + 2y.
To find dz/dy, we differentiate the function z = -8x³ - 5y² + 2xy with respect to y while treating x as a constant. The derivative of -5y² with respect to y is -10y, and the derivative of 2xy with respect to y is 2x. Therefore, dz/dy = -10y + 2x.
To find dz/dx(5, -5), we substitute x = 5 and y = -5 into dz/dx: dz/dx(5, -5) = -24(5)² + 2(-5) = -600 - 10 = -610.
Similarly, to find dz/dy(5, -5), we substitute x = 5 and y = -5 into dz/dy: dz/dy(5, -5) = -10(-5) + 2(5) = 50 + 10 = 60.
Lastly, to find ayz(5, -5) for question 6.2.3, part 1 of 4, we substitute x = 5 and y = -5 into the given function z: ayz(5, -5) = -8(5)³ - 5(-5)² + 2(5)(-5) = -200 - 125 - 50 = -375.
Therefore, dz/dx = -24x² + 2y, dz/dy = -10y + 2x, dz/dx(5, -5) = -610, dz/dy(5, -5) = 60, and ayz(5, -5) = -375.
To learn more about partial derivatives: -brainly.com/question/28750217#SPJ11
Time (hours) 2 4 6 8
Distance (miles) 8 16 24 32
Is the linear relationship also proportional? Explain.
Yes, the constant of proportionality is 4.
Yes, there is no constant of proportionality.
No, the constant of proportionality is 4.
No, there is no constant of proportionality.
Answers
The linear relationship between time and distance can be considered proportional. The constant of proportionality in this case is 4.
In a proportional relationship, the ratio between the two quantities remains constant. Here, as time increases by 2 hours, the distance also increases by 8 miles. Let's calculate the ratio of distance to time for each pair of values:
For the first pair (2 hours, 8 miles):
Ratio = distance / time = 8 miles / 2 hours = 4 miles/hour
For the second pair (4 hours, 16 miles):
Ratio = distance / time = 16 miles / 4 hours = 4 miles/hour
For the third pair (6 hours, 24 miles):
Ratio = distance / time = 24 miles / 6 hours = 4 miles/hour
For the fourth pair (8 hours, 32 miles):
Ratio = distance / time = 32 miles / 8 hours = 4 miles/hour
As we can see, the ratio of distance to time remains constant at 4 miles per hour for all the pairs. This indicates a proportional relationship between time and distance.
Therefore, the linear relationship is also proportional, and the constant of proportionality is 4.
To know more about proportional relationships, refer here:
https://brainly.com/question/29765554#
#SPJ11
Rewrite 24 as an improper fraction
Answers
Answer:
48/2
Step-by-step explanation:
you can just multiply it by the denominator to make any number an improper fraction
What is distance formula and example?
Answers
The distance formula is a mathematical equation used to find the distance between two points in a plane. These two points can be represented in the form of (x1, y1) and (x2, y2), where x and y are the coordinates on the x-axis and y-axis respectively.
The distance formula can be used to calculate the distance between two points in various fields like geometry, physics, and engineering. The formula to calculate the distance between two points (x1, y1) and (x2, y2) is given as: distance = √((x2 - x1)^2 + (y2 - y1)^2). Here, (x2 - x1) and (y2 - y1) are the differences in the x-coordinates and y-coordinates of the two points. The square root sign (√) is used to find the magnitude or length of the line segment connecting the two points. The exponent ‘^2’ is used to square the difference of the coordinates.
Let's consider an example to understand the distance formula better. If the two points are (2, 3) and (6, 8), then the distance between these two points can be calculated as follows: distance = √((6 - 2)^2 + (8 - 3)^2) = √(4^2 + 5^2) = √(16 + 25) = √41 = approximately 6.4. In this example, the distance between the two points (2, 3) and (6, 8) is 6.4 units. The distance formula can be used to calculate the distance between any two points in a plane.
For more such questions on Distance formula.
https://brainly.com/question/28956738#
#SPJ11