DUE AT 11:59 PLEASE HELP Only if you are good at geometry.
Describe a Sequence of Transformations that would map Triangle SRT onto S'RT. *

Answers
Answer:
- reflection about the x-axis
- translation down 2 units
- translation right 3 units
Step-by-step explanation:
Related Questions
You are observing a radioactive decay process where you expect 3 atoms to decay every minute. Use the normal distribution to approximate the number of decaying atoms that you will see in 1 hour. Provide the following: the mean of the normal distribution the standard deviation of the normal distribution P(# of decays in 1 hour =180)
Answers
The radioactive decay process in which 3 atoms are expected to decay every minute can be modeled using the Poisson distribution. The average rate of decay (λ) is 3 per minute, so the mean of the Poisson distribution is λ × t, where t is the time period in minutes.
In this case, the time period is 60 minutes (1 hour), so the mean is λ × t = 3 × 60 = 180. The standard deviation of the Poisson distribution is also √(λ × t), which is √(180) ≈ 13.42.
Specifically, we need to subtract 0.5 from the lower bound and add 0.5 to the upper bound of the interval that we are interested in. In this case, we are interested in the interval [179.5, 180.5], since we want to know the probability of observing exactly 180 decays.
The continuity correction gives us P(179.5 < X < 180.5), where X is normally distributed with mean 180 and standard deviation 13.42.Using the standard normal distribution, we can standardize X as follows:
z = (X - μ) / σ = (180 - 180) / 13.42 ≈ 0
Therefore, we need to find the probability that z is between (179.5 - 180) / 13.42 ≈ -0.04 and (180.5 - 180) / 13.42 ≈ 0.04, which is the same as finding the probability that z is between -0.04 and 0.04.
Using a standard normal table or calculator, we find this probability to be approximately 0.0314.
Therefore,P(# of decays in 1 hour = 180) ≈ P(179.5 < X < 180.5)≈ P(-0.04 < z < 0.04)≈ 0.0314 (rounded to four decimal places).
To know more about Poisson distribution visit:
https://brainly.com/question/30388228
#SPJ11
Given a radioactive decay rate of 3 atoms per minute, the mean of the normal distribution for decays in one hour is 180 and the standard deviation is approximately 13.42. The probability of exactly 180 decays in one hour can be found using the normal distribution with this mean and standard deviation.
Explanation:To calculate about the radioactive decay process where we expect 3 atoms to decay every minute, we need to use the normal distribution. In this case, we are asked to approximate the number of decaying atoms we'll see in 1 hour (60 minutes).
The mean (expected value) μ of a Poisson distribution is simply the rate (λ) which, in this case, is the number of decays we expect every minute. Over the course of 60 minutes (1 hour), we expect 3 decays/minute * 60 minutes = 180 decays. So, the mean of the normal distribution for this problem is 180.
The standard deviation σ of a Poisson distribution is simply the square root of the mean. So σ = √180 ≈ 13.42.
As for the last part of the question, the probability that exactly 180 decays will occur in 1 hour P(# of decays in 1 hour =180) is given by the normal distribution with mean 180 and standard deviation 13.42.
Learn more about Radioactive Decay here:https://brainly.com/question/1770619
#SPJ11
Please help, doing age word problems. Tysm if you do, really appreciated :D
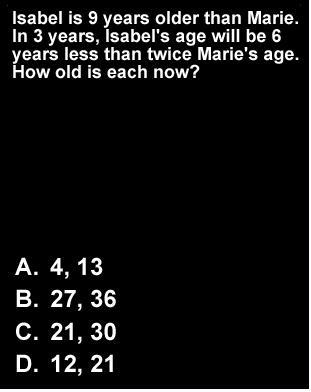




Answers
Answer:
D (12, 21); B (11, 17); C (18,28); D (42); C (8).
Step-by-step explanation:
First:
Let I represent Isabel and M represent Marie.
We know that currently, Isabel is 9 years older than Marie, or:
I=9+M.
In three years, Isabel will be six years less than twice of Marie's age. In other words:
(I+3)= 2(M+3)-6
Now solve. Substitute I.
(9+M+3)=2M+6-6
12+M=2M
M=12; I=21. Marie is 12 while Isabel is 21.
Second:
Let I represent Isabel and M represent Marie.
Isabel is 6 years older than Marie; in other words: I=6+M
In 4 years, Isabel will be 9 years less than twice Marie's age. Or:
(I+4)=2(M+4)-9
Solve. Substitute I.
(6+M+4)=2(M+4)-9
10+M=2M+8-9
10+M=2M-1
11=M; I=17; Marie is 11 while Isabel is 17.
Third:
Let I represent Isabel and M represent Marie.
Isabel is 10 years older than Marie, or: I=10+M
In 2 years, twice Isabel's age is three times Marie's age. Or:
2(I+2)=3(M+2)
Solve. Substitute for I.
2(10+M+2)=3(M+2)
24+2M=3M+6
18=M; I=28. Marie is 18 while Isabel is 28.
Fourth:
Let M represent Mary and A represent Ann.
Mary is 3 time as old as Ann. Or: M=3A
7 years ago Mary was 5 times as old as Ann. In other words:
(M-7)=5(A-7)
Solve for this system. Substitute M.
(3A-7)=5A-35
-2A=-28
A=14; M=42; Mary is 42.
Fifth:
Let T represent Tammy and L represent Laurel.
We know that Tammy is 42 while Laurel is 9. In other words:
T=42 and L=9.
We need to find in how many years will 3 times Laurel's age be 1 more than Tammy's age. In other words, let's let y represent the amount of years. Thus:
3(L+y)=(T+y)+1
We already know L and T:
3(9+y)=(42+y)+1
27+3y=43+y
2y=16
y=8
In 8 years, when Laurel is 17 and Tammy is 50. (3 times 17 is 51, one more than 50).
Step-by-step explanation:
Problem 1 :Since we have the answers no need to write an equation and solve it
4 and 13 : substract 3 from each : 1 , 10 so Isabel is really 9 years older than Marie add 3 : 7 and 16 16+6 = 21 = 7*3 so that's rightthe answer is A
Problem 2 : 11 and 17 17 -11 = 6 so that's right add 4 to each : 17+4 = 21 11+4= 15 21+9 = 30= 15*2 so that's rightb is the answer
Problem 3 : 18 and 28 28-18= 10 so it's a good choice add 2 : 30 and 20 30*2= 60 and 20*3 = 60so that's true !C is the answer
Problem 4 : here i have a method let x be the age of Marie and y the age of Ann Mary is 3 times as old as Ann so : x = 3y 7 years ago Mary was 5 times as old as An so x-7 = 5(y-7) solve the equations and you'll get y= 14 so x = 3*y = 3*14= 42So the answer is D
Problem 5 : 42 + 8 = 50 and 8+9= 17 17*3 = 51 51-50 = 1 so the answer is 8 yearsThe answer is c
Michael buy a baket of mangoe on ale for \$ 4$4 before tax.
The ale tax i 12%.
What i the total price Michael pay for the baket of mangoe?
Answers
Total price paid by Michael for the basket of mangoes is $4.48.
For the calculation of total price, price of sales tax will be added with selling price. Forming the equation -
Total price = 4 + 12%×4
Calculating the percentage of sales tax on Right Hand Side of the equation
Total price = 4 + 12×4/100
Solving the percentage part on Right Hand Side of the equation
Total price = 4 + 0.48
Performing addition on Right Hand Side of the equation
Total price = $4.48
Hence, Michael has to pay $4.48 after addition of sales tax for the basket of mangoes.
Learn more about sales tax -
https://brainly.com/question/9437038
#SPJ4
Learn more
The value of Maggie's car decreased by 10% since last year, when she bought it. If the car is now worth $16,000.00, how much was the car worth when she bought it?
Answers
Answer: 17600
Step-by-step explanation: 16000*10% is the same as 16000*0.1, then you get 1600. 16000+ 1600 is 17600
if v²=u²+2gs, find te value of s when v = 25 , u = 12 and g = 10
Answers
The value of s for the given value is 24.05.
Given is an equation v² = u²+2gs, we need to find the value of s if v = 25, u = 12 and g = 10,
So,
25² = 12² + 2(10)s
625 = 144 + 20s
20s = 481
s = 24.05
Hence the value of s for the given value is 24.05.
Learn more about equation click;
https://brainly.com/question/29657983
#SPJ1
How do I find the maximum height, maximum volume, and maximum weight of a cone when I only know the angle of repose, radius and density?
Answers
In order to find the maximum height, maximum volume, and maximum weight of a cone when only the angle of repose, radius, and density are known, the following steps can be followed:
Step 1: Find the height of the cone using the angle of repose. The angle of repose is the maximum angle at which an object can be tilted before it starts to slide. The tangent of this angle is equal to the coefficient of static friction between the object and the surface on which it is resting.
Using the radius and the angle of repose, the height of the cone can be calculated as follows:tan(angle of repose) = height/radius height = radius * tan(angle of repose).
Step 2: Calculate the volume of the cone. The formula for the volume of a cone is:V = (1/3) * π * r^2 * h, Where V is the volume, r is the radius, and h is the height obtained in step 1.
Using these values, the maximum volume of the cone can be calculated.Step 3: Calculate the weight of the cone. The weight of the cone can be calculated using the formula: W = m * g, Where W is the weight, m is the mass, and g is the acceleration due to gravity.
The mass can be calculated using the formula:m = (density) * (volume)Using the maximum volume obtained in step 2 and the density given, the maximum weight of the cone can be calculated.
For more question on density
https://brainly.com/question/1354972
#SPJ8
The local library lends an average of 68.24 books to readers each day. What is the average number of books lent to readers in a week?
Answers
Answer:
Step-by-step explanation:
Set this up as a proportion and solve. The ratios are books:day, so keep in mind that a week is 7 days because your values have to be the same
\(\frac{books}{day}:\frac{68.24}{1}=\frac{x}{7}\) and cross multiply to solve for x, the number of books lent out in a week:
x = 68.24(7) so
x = 477.68 books in a week
The ize of a rectangle i 25 cm by 16 cm. A quare ha the ame area a the rectangle. Find the
perimeter of the quare
Answers
The square has a 48 centimeter perimeter.
To find the perimeter of the square, we need to calculate its side length. The area of a rectangle is given by its length multiplied by its width, so we can use the given measurements of the rectangle to calculate its area: 25 cm x 16 cm = 400 cm². The area of a square is given by the square of its side length, so we can use the area of the rectangle to calculate the side length of the square: √400 cm² = 20 cm.
Thus, the perimeter of the square is equal to 4 times its side length, or 4 x 20 cm = 80 cm.
Learn more about square here
https://brainly.com/question/29192128
#SPJ4
math question
13 c= pt
Answers
Step-by-step explanation:
13 cups = ? pints
there are 2 cups per pint so:
13/2 = 6.5
13 cups = 6.5 or \(6\frac{1}{2}\) pints
The p-value Question 14 options: can be any negative value. can be any positive value. must be a number between -1 and 0. must be a number between zero and one.
Answers
The correct answer is that the p-value must be a number between zero and one.
The p-value is a crucial statistical tool in hypothesis testing. It is defined as the probability of obtaining the observed outcome, or any outcome more extreme than it, given the null hypothesis is true.
The p-value measures the strength of the evidence against the null hypothesis. In general, the smaller the p-value, the stronger the evidence against the null hypothesis. Therefore, the p-value must be a number between zero and one.
When a p-value is close to zero, it indicates that the probability of observing the observed outcome under the null hypothesis is very low.
In contrast, when a p-value is close to one, it indicates that the observed outcome is very likely to have occurred by chance under the null hypothesis. In hypothesis testing, a p-value less than or equal to the significance level (usually 0.05) is considered significant.
If the p-value is significant, the null hypothesis is rejected, and the alternative hypothesis is supported. If the p-value is not significant, the null hypothesis is not rejected, and no conclusion can be drawn about the alternative hypothesis.
The p-value cannot be negative or outside the range of 0 to 1. Therefore, the correct answer is that the p-value must be a number between zero and one.
For more such questions on p-value
https://brainly.com/question/13786078
#SPJ8
the following table shows the number of miles a hiker walked on a trail each day for 6 days. day 1 2 3 4 5 6 number of miles 8 5 7 2 9 8 what was the mean number of miles the hiker walked for the 6 days? responses 3.5 3.5 4.5 4.5 6.5 6.5 7.5 7.5 8
Answers
The mean number of miles the hiker walked for the 6 days was 6.5 miles.
To calculate the mean or average of a set of numbers, we add up all the numbers and then divide the sum by the number of items in the set. In this case, we have the number of miles the hiker walked on each of the six days. To find the total number of miles the hiker walked, we simply add up all the numbers
8 + 5 + 7 + 2 + 9 + 8 = 39
Next, we divide the total number of miles by the number of days (which is 6) to get the average or mean number of miles the hiker walked per day:
Mean number of miles = Total number of miles / Number of days
= 39 / 6
= 6.5
Learn more about mean here
brainly.com/question/22871228
#SPJ4
Which one could it be?

Answers
Find the value of each variable. Help asappppp

Answers
Answer:
x = 24 , y = 24√3 = 41.57
Step-by-step explanation:
In the triangle,
sin 30° = x/48
1/2 = x/48
48 = 2x
24 = x ---------- (1)
Then,
tan 30° = x/y
1/√3 = 24/y [from (1)]
y = 24√3
y = 24 × 1.732
y = 41.57 [approx.]
Hope it helps ⚜
cystic fibrosis is a rare disease caused by homozygosity for a recessive and autosomal allele, and characterized by a build-up of mucus in the lungs and difficulty breathing. a woman whose maternal uncle had the disease is trying to determine the probability she and her mate could have an affected child. her mate's sister died of the disease. assuming the uncle and the sister are the only family members who had the disease, what is the chance that the couple's first child will be unaffected?
Answers
The chances that the couple's first child will be affected by cystic fibrosis is given by probability factor as 25% that is 1/4.
The lungs, digestive system, and other bodily organs are severely harmed by cystic fibrosis (CF), a genetic condition.
The cells that make mucus, perspiration, and digestive fluids are impacted by cystic fibrosis. Normally, these produced fluids are slick and thin. Nevertheless, a faulty gene in CF patients makes the secretions thick and sticky. The secretions clog up tubes, ducts, and passages rather of lubricating them, particularly in the pancreas and lungs.
The likelihood of the couple's first child developing cystic fibrosis is 25% (or 1 in 4) because the pair appears to be CFTR gene carriers.
Children of CF carriers can inherit their copy of the CFTR gene mutation. Every time two CF carriers conceive a child together, there is a 25% chance that the child will have CF, a 50% chance that the child will be a carrier, and a 25% chance that the child won't be a carrier and won't have CF.
Learn more about cystic fibrosis :
https://brainly.com/question/3303086
#SPJ4
If f(x) = -2x + 8, and f(k) = -10, what is the value
of k? step by step please
Answers
Answer:
Value of k is 9
Step-by-step explanation:
-2x + 8 = -10
-2x = -10 - 8
-2x = -18
x = -18/-2
x = 9
f(x) = f(k)
x = k
9 = k
Hello there!
We are given the function:
\( \displaystyle \large{f(x) = - 2x + 8}\)
We want to find the value of k. First, we know that f(k) is -10. We substitute x = k and f(x) = -10.
\( \displaystyle \large{f(k) = - 2k + 8} \\ \displaystyle \large{ - 10 = - 2k + 8}\)
Solving the equation. First, we subtract both sides by 8.
\( \displaystyle \large{ - 10 - 8 = - 2k +8 - 8} \\ \displaystyle \large{ - 18 = - 2k} \\ \)
Divide both sides by -2.
\( \displaystyle \large{ \frac{ - 18}{ - 2} = \frac{ - 2k}{ - 2} } \\ \displaystyle \large{ 9= k}\)
Therefore, k = 9
When we substitute k = 9 in f(k), the value is -10.
Let me know if you have any questions!
Topic: Linear Function
f(x) = 2x+3 and g(x) = x - 7. Find f(3)
Answers
Answer:
f(3) = 9
Step-by-step explanation:
To evaluate f(3) substitute x = 3 into f(x), that is
f(3) = 2(3) + 3 = 6 + 3 = 9
Answer:
f(3) = 9
Step-by-step explanation:
f(3) = 2x + 3
input the 3 into all x values since it is f(x) basically it tells you the value of x
f(3) = 2(3) + 3
f(3) = 9
the perimeter of a rectangle is 40 cm. two of his sides measure 12.9 cm and 14.6 cm find the length of its third side.
Answers
Answer:
the third side is 12.6 centimeters
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
Using the results from the regression analysis in the Excel
document (Question 10), what is the estimated milk production
rounded to the nearest whole number?
A. 105,719 gallons of milk
B. 53 gallons
Answers
Based on the information provided, the estimated milk production rounded to the nearest whole number is 105,719 gallons of milk.
The estimated milk production value of 105,719 gallons is obtained from the regression analysis conducted in the Excel document. Regression analysis is a statistical technique used to model the relationship between a dependent variable (in this case, milk production) and one or more independent variables (such as time, weather conditions, or other relevant factors). The analysis likely involved fitting a regression model to the available data, which allows for estimating the milk production based on the variables considered in the analysis.
To know more about statistical technique here: brainly.com/question/32688529
#SPJ11
what does it mean to say that an allele is "fixed"?
Answers
Answer:
When we say that an allele is "fixed," it means that a particular allele has reached a frequency of 100% in a population.
Step-by-step explanation:
Alleles are different forms of a gene that occupy the same position on homologous chromosomes. In a population, different alleles can exist for a specific gene. However, through various evolutionary processes such as natural selection, genetic drift, or gene flow, one allele may become predominant and eventually fixate within the population.
The fixation of an allele can occur through different mechanisms. For example, if a beneficial allele provides a selective advantage to individuals carrying it, it is more likely to increase in frequency and eventually become fixed in the population. On the other hand, genetic drift, which is the random change in allele frequencies due to chance events, can also lead to the fixation of an allele, especially in small populations.
Once an allele is fixed in a population, it means that all future generations will inherit that allele, and no alternative alleles will be present at that particular gene locus.
Learn more about allele here, https://brainly.com/question/3452155
#SPJ11
How you used the limit definition of a derivative to calculate the instantaneous acceleration. use your results to explain why the limit definition of a derivative is tru
Answers
The instantaneous acceleration at any time t is given by 10t. The limit definition of a derivative is true because it allows us to find the instantaneous rate of change of a function at a specific point.
To use the limit definition of a derivative to calculate instantaneous acceleration, we need to find the derivative of the velocity function with respect to time. The derivative of velocity gives us acceleration.
The limit definition of a derivative is given by:
f'(x) = lim (h→0) [f(x+h) - f(x)] / h
To calculate instantaneous acceleration, we substitute the velocity function, v(t), into the limit definition. Let's say v(t) = 5t^2.
Using the limit definition, we have:
a(t) = lim (h→0) [v(t+h) - v(t)] / h
Substituting v(t) = 5t^2, we get:
a(t) = lim (h→0) [5(t+h)^2 - 5t^2] / h
Expanding and simplifying:
a(t) = lim (h→0) [10th + 5h^2] / h
Now, we can cancel out the h term:
a(t) = lim (h→0) 10t + 5h
Taking the limit as h approaches 0, we get:
a(t) = 10t
Therefore, the instantaneous acceleration at any time t is given by 10t.
The limit definition of a derivative is true because it allows us to find the instantaneous rate of change of a function at a specific point. By taking the limit as the change in input approaches zero, we are able to approximate the exact rate of change at that point. This concept is fundamental to calculus and is used in various applications such as physics, engineering, and economics.
Learn more about acceleration
https://brainly.com/question/2303856
#SPJ11
An artists creates a scale model of a sculpture with a scale of 2 inches = 5 feet. if the scale moderl of the sculpture measures 8 inches tall, how many feet tall is the actual sculpture?
Answers
Answer:
The actual sculpture is 20 feet.
-
Step-by-step explanation:
\( \frac{2 \: inches}{5 \: feet} = \frac{8 \: inches}{x} \\ \\ \frac{40}{2} = \frac{2x}{2} \\ \\ x = 20\)
Set up, but do not evaluate, an integral for the length of the curvey=cosx,0≤x≤2π.Length of Curve:For any function, length of curve is the measure of the distance between two points on the curve. It can be calculated mathematically with the help of setting an integral between the two given points.L=∫βα√1+(dydx)2 dxHere, α and βare the two given points.
Answers
The given expression y=cos x is solved using the arc length formula. And, the required integral or curve length is \(L=\int\limits^{2\pi}_0 \sqrt{1+\sin^2x} \, dx\).
The length of the curve or the arc length helps to determine the distance between one point to another point in the curve. This is calculated by using the integral formula between two given points,
\(L=\int\limits^b_a \sqrt{1+\left(\frac{dy}{dx}\right)^2} \, dx\)
The given expression is y=cosx and the limit is 0≤x≤2π. First, differentiate the given expression concerning x, we get,
dy/dx= -sin x
Then, squaring both sides of the above expression,
(dy/dx)²= sin²x
Now, substituting (dy/dx)² in the formula, we get,
\(L=\int\limits^{2\pi}_0 \sqrt{1+\sin^2x} \, dx\)
Therefore, the above expression is the required answer.
To know more about arc length:
https://brainly.com/question/30688993
#SPJ4
The complete question is -
Set up, but do not evaluate, an integral for the length of the curve y=cosx, 0≤x≤2π.
If G¹(x) is the inverse of G(x), what is the value of G¹(G(x))?
Ο A. x
OB. x¹
O C. 1
OD. O
SUBMIT
Answers
The value of G⁻¹(G(x)) is x , So the correct answer among the following options is A) x
What is function?
A function is described as a relationship between a set of inputs and one output for every one of them. Simply described, a function is an association of inputs where each input is coupled to a single, distinct output. Each function has a codomain or range.
What is inverse function?An inverse function, sometimes known as an antI function, is a function that can change into another function. In other words, if any function "f" takes x → y, then the inverse of that function will take y to x. The inverse of a function denoted by "f" or "F" is denoted by "f-1" or "F-1." Not to be mistaken with an exponent or a reciprocal in this case is (-1).
Given, function G(x)
inverse of the given function G⁻¹(x)
Let G(x) = x
Then G⁻¹(x) = x
So value of G⁻¹(G(x)) is,
Put G(x) = x,
Hence, G⁻¹(G(x)) = x
To learn more about function, visit :-
https://brainly.com/question/2541698
#SPJ1
Whats the length of each side of a cube if density was 8.2g/cm^3 and mass is 4.0kg?
Answers
32kg is the answer....
which of the following statements do you believe are true? in a normal distribution - a) approximately 70% of the values are within one standard deviation from the mean, b) twenty-seven percent of the values are between one and two standard deviations from the means. c) 2.1% of the values are between -2 and -3 standard deviations from the mean. d) .1% of the values are 3 of higher standard deviations from the mean. e) all the alternatives are correct. f) none of the alternatives are correct. g) only a and b are correct. h) only c and d are correct.
Answers
The correct statement is "only a and c are correct" so option g is the answer.
The statement that is true in a normal distribution is "approximately 70% of the values are within one standard deviation from the mean" (a), and "2.1% of the values are between -2 and -3 standard deviations from the mean" (c).
These statements are true because of the properties of a normal distribution, also known as a Gaussian distribution or bell curve. In a normal distribution, the majority of values cluster around the mean, with fewer and fewer values as you move further away from the mean.
The statement "twenty-seven percent of the values are between one and two standard deviations from the mean" (b) is not true, as the correct percentage is approximately 27.7% (68-95-99.7 rule).
The statement "0.1% of the values are 3 or higher standard deviations from the mean" (d) is also not true, as the correct percentage is approximately 0.3%.
Therefore, the correct statement is "only a and c are correct".
To learn more about standard deviation:
https://brainly.com/question/475676
#SPJ4
Submission in an houuuur!!! Please send help and can I please have the explanation.

Answers
Answer:
It should 3/10
Step-by-step explanation:
(500,100,20,4) common ratio in the following sequences m
Answers
The 7th term in this geometric sequence is 3.2.
We have,
To determine the common ratio in a geometric sequence, we can divide any term by its preceding term.
Let's apply this to the given sequence: 500, 100, 20, 4.
First, let's divide each term by its preceding term:
100 / 500 = 0.2
20 / 100 = 0.2
4 / 20 = 0.2
We observe that each term divided by its preceding term gives us the same value, which is 0.2.
Therefore, the common ratio in this sequence is 0.2.
To find the 7th term, we can use the formula for the nth term of a geometric sequence:
\(a_n = a_1 \times r^{n-1},\)
where \(a_n\) is the nth term, \(a_1\) is the first term, r is the common ratio, and n is the position of the term.
In this case, the first term \(a_1\) is 500, the common ratio r is 0.2, and we want to find the 7th term \(a_7\).
Plugging these values into the formula, we have:
\(a_7 = 500 \times 0.2^{7-1}\)
= 500 x \(0.2^6\)
= 500 x 0.0064
= 3.2
Therefore,
The 7th term in this geometric sequence is 3.2.
Learn more about geometric sequence here:
https://brainly.com/question/2321576
#SPJ1
What is the equation in point-slope form of the line that passes through the point (4,-5) and has a slope of 2/3?

Answers
Answer: I believe the correct answer is the last one but I’m not entirely sure, wait for someone else to answer.
Step-by-step explanation:
Answer:
third one
Step-by-step explanation:
point-slope form is y - y1 = m(x - x1)
plug in values y -(-5) = 2/3(x - 4)
the double negative cancels out and becomes a positive
therefore y + 5 = 2/3(x - 4)
URGENT!
How do you I know if there's 2 possible triangles for an ambiguous case?
Answers
Answer: ?Once you find the value of your angle, subtract it from 180° to find the possible second angle. Add the new angle to the original angle. If their sum is less than 180°, you have two valid answers. If the sum is over 180°, then the second angle is not valid??????
Step-by-step explanation: