Answers
We have to find the value of x.
Related Questions
Compute the probability of X successes using the binomial formula. Round your answers to three decimal places as needed. n=8, p=0.39, X=3
Answers
The probability of getting exactly 3 successes in 8 trials, with a success probability of 0.39, is 0.019 or 1.9%.
How is Probability calculated?The chance of X successes in n separate trials, where each trial has a probability of success of p, is calculated using the binomial formula. The likelihood of 3 successes in 8 tries, with a success probability of 0.39, may be calculated using this method. This is the binomial formula:
P(X = k) is equal to (n pick k) * p * k * (1-p) (n-k)
Where (n pick k) denotes the variety of ways to select k successes from n trials, n is the number of trials, k is the number of successes, p is the probability of success, and so on.
We can enter the values provided in the formula using the following:
P(X = 3) = (8 pick 3) (8 choose 3) * (0.39)^3 * (1-0.39)^(8-3) (8-3)
P(X = 3) = (8! / (3! * (8-3)!)) * (0.39)^3 * (0.61)^5
P(X = 3) = (56) * (0.039304) * (0.088848) (0.088848)
P(X = 3) = 0.019
Learn more about Probability here:
brainly.com/question/30034780
#SPJ1
Please help with the following question.

Answers
The probabilities, using the Poisson distribution, are given as follows:
a) Two earthquakes in a year: 0.0446 = 4.46%.
b) No earthquakes in two consecutive months: 0.3679 = 36.79%.
c) No earthquakes in two consecutive months, given that there were no earthquakes in the previous month: 0.3679 = 36.79%.
What is the Poisson distribution?The Poisson distribution is used when we only have the mean in a given interval and the mass function is given as follows:
\(P(X = x) = \frac{e^{-\mu}\mu^{x}}{(x)!}\)
The parameters are listed as follows:
x is the number of successes.e = 2.71828 is the Euler number.\(\mu\) is the mean in the given interval or range of values of the input parameter.For one year, the mean number of earthquakes is given as follows:
\(\mu = 6\)
The probability of exactly two earthquakes in a year is obtained as follows:
\(P(X = x) = \frac{e^{-\mu}\mu^{x}}{(x)!}\)
\(P(X = 2) = \frac{e^{-6}6^{2}}{(2)!} = 0.0446\)
For two months, the mean is given as follows:
\(\mu = 2 \times 6 \times \frac{1}{12} = 1\)
For items b and c, the probabilities are the same, P(X = 0), as the events are independent, hence:
\(P(X = x) = \frac{e^{-\mu}\mu^{x}}{(x)!}\)
\(P(X = 0) = \frac{e^{-1}1^{0}}{(0)!} = 0.3679\)
More can be learned about the Poisson distribution at https://brainly.com/question/7879375
#SPJ1
33% of adults say cashews are their favorite kind of nut. You randomly select 12 adults and ask each to name his or her favorite nut. Find the probability that the number who say cashews are their favorite nut is (a) exactly three, (b) at least four, and (c) at most two. If convenient, use technology to find the probabilities. Due Saturday night
Answers
The cumulative probability is
P(at most 2 ) = 0.187560896 [answer]
How to solvea)
Note that the probability of x successes out of n trials is
P(n, x) = nCx p^x (1 - p)^(n - x)
where
n = number of trials = 12
p = the probability of a success = 0.33
x = the number of successes = 3
Thus, the probability is
P ( 3 ) = 0.21509867 [answer]
***********
b)
Note that P(at least x) = 1 - P(at most x - 1).
Using a cumulative binomial distribution table or technology, matching
n = number of trials = 12
p = the probability of a success = 0.33
x = our critical value of successes = 4
Then the cumulative probability of P(at most x - 1) from a table/technology is
P(at most 3 ) = 0.402659566
Thus, the probability of at least 4 successes is
P(at least 4 ) = 0.597340434 [answer]
***************
c)
Using a cumulative binomial distribution table or technology, matching
n = number of trials = 12
p = the probability of a success = 0.33
x = the maximum number of successes = 2
Then the cumulative probability is
P(at most 2 ) = 0.187560896 [answer]
Read more about cumulative probability here:
https://brainly.com/question/25870256
#SPJ1
You start savings a $250 a month for the next 22 years to give us a gift to your daughter when she graduates college if you put the money into a long-term savings account that receives 3.5 interest how much money will you be able to give your daughter
Answers
Answer:
$376,475.71
Step-by-step explanation:
FVA Due = P * [(1 + r)n – 1] * (1 + r) / r
FVA Due = 250 * [(1.2916)264 – 1] * (1.2916) / .2916
Two similar rectangles have a scale factor of 2:4. The perimeter of the large rectangle
is 80 meters. Find the perimeter of the small rectangle.
Answers
Answer:
scale factor 2:4
80÷4×2=40
The perimeter of the large rectangle is 40 meters.
What are ratios and proportions?An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. The numerical relationship between two values demonstrates how frequently one value contains or is contained within another.
The perimeter is defined as the sum of all the sides of the rectangle.
Given that two similar rectangles have a scale factor of 2:4. The perimeter of the large rectangle is 80 meters.
The perimeter of the small rectangle will be calculated as,
S / L = 2 / 4
S = ( L x 2 ) / 4
S = ( 80 x 2 ) / 4
S = 40 meters
To know more about ratios and proportions follow
https://brainly.com/question/2914376
#SPJ2
The accompanying data are lengths (inches) of bears. Find the percentile corresponding to 61.0 in.
(Round to the nearest whole number as needed.)
Bear Lengths
36.0 37.0 39.5 40.0 40.5 43.0 44.0 45.5 45.5 46.5 48.0 48.00 49.0 50.0 51.5 52.5 53.0 53.5 54.0 57.3 57.5 58.0 58.5 59.0 59.5 60.0 61.0 61.0 61.0 61.5 62.0 62.5 63.0 63.0 63.5 64.0 64.0 64.0 64.5 65.0 66.0 67.5 67.5 68.5 70.0 70.5 71.5 72.0 72.5 72.5 72.5 73.5 74.5 77.5
Answers
Answer:
52nd percentile
Step-by-step explanation:
The sorted data :
36.0, 37.0, 39.5, 40.0, 40.5, 43.0, 44.0, 45.5, 45.5, 46.5, 48.0, 48.00, 49.0, 50.0, 51.5, 52.5, 53.0, 53.5, 54.0, 57.3, 57.5, 58.0, 58.5, 59.0, 59.5, 60.0, 61.0, 61.0, 61.0, 61.5, 62.0, 62.5, 63.0, 63.0, 63.5, 64.0, 64.0, 64.0, 64.5, 65.0, 66.0, 67.5, 67.5, 68.5, 70.0, 70.5, 71.5, 72.0, 72.5, 72.5, 72.5, 73.5, 74.5, 77.5
The total size of the data = 54
The value 61.0 occurs in position ; 27th, 28th and 29th
Taking the position average :
(27+28+29)/3 = 84/3 = 28th position
This means the percentile score of 61 is :
(Position average / total size) * 100%
(28/54) * 100%
0.5185185 * 100%
= 51.85%
This means that 61 inch length falls in the 52nd percentile
someone help me
please and thank you

Answers
Answer: Answer C
Step-by-step explanation:
Because it is a reflection of the Y-axis, the X-coordinates would remain the same but the Y-coordinates would change.
9(k+12)+4k2 when k= 3 the 2 is small
Answers
Answer:
the answer is 4k^2+9k+108
Step-by-step explanation:
Answer:
171
Step-by-step explanation:
When you say "the 2 is small" I think you mean it's an exponent so the equation would look like....
\(9(k+12) + 4k^{2}\)
if k=3 we would replace all the k's with 3.
9(3+12) + 4(3)²
9(15) + 4(9)
135 + 36
171
So the answer would be 171
Hope that helps and have a great day!
Jacob spent 5 hours skiing and snowboarding. He skied for 2 hours 10 minutes.
How long did he spend snowboarding?
Answers
Answer:
he spent 2hours 50minutes snowboarding
the time he spent skiing and snowboarding minus the time he skied
5hours minus 2hours 10minutes
Solve for 10 and 12 please and thank you

Answers
Answer:
10. 120 Degrees 12. 60 Degrees
Step-by-step explanation:
#12. Since CAD is 30, and BAD is a 90 degree angle, angle BAF is 60 degrees. Since BAF is 60 degrees and FAE and BAF are vertical angles, they have the same angle measure. 60 Degrees.
#10. Since BAF is 60, and FAE and BAF are on a line, we can do 180-60 to get the measure in degrees of that angle. FAE = 120 Degrees.
Answer:
Step-by-step explanation:
10. somewhere between 126 and 129, i feel its 128
12. between 60 and 65
Which rule explains why these triangles are
congruent?
U
T
V
W
AAS
ASA
SAS
SSS
These triangles
cannot be proven
congruent.

Answers
These triangles can be proven congruent by using ASA RULE.
What is congruent triangles and its rules ?
When two triangles are congruent, their three sides and their three angles match precisely.
If there is a turn or a flip, the equal sides and angles might not be in the same place, but they are still present.
ASA rule stands for Angle-Side-Angle rule which means two angles and a side of both triangles are equal.
Main Body:
In ΔTUV and ΔTWV
VT =VT ----(1)
∠VTU=∠TVW -----(2)
As TUVW is a parallelogram
so, ∠T = ∠U
hence, ∠TVU =∠VTW ----(3)
taking equation 1, 2,3
therefore, ΔTUV ≅ ΔTWV by ASA rule which means by Angle- Side- Angle rule.
to learn more about congruency click on the link below
https://brainly.com/question/1675117
#SPJ13
How did waterways provide Detroit with such a vital military position?
Answers
Answer:
Your source water comes from the Detroit River, situated within the Lake St. Clair, Clinton River, Detroit River, Rouge River and Ecorse River watersheds in the U.S., and parts of the Thames River, Little River, Turkey Creek and Sydenham watersheds in Canada.
Step-by-step explanation:
please mark this answer as brainliest
lect the correct answer.
Under which condition is the sample proportion, , a point estimate of the population proportion?
A.
The sample proportion is never a point estimate of the population proportion.
B.
The sample represents a proportion of the population.
C.
The sample proportion is unbiased.
D.
The sample size, n, is small enough.
Reset Next
Answers
The correct answer is B. The sample represents a proportion of the population.
What is the sample population ?
A point estimate is a single value used to estimate a population's unknown parameter. The sample proportion (denoted by p), in the context of determining the population proportion, is a widely used point estimate. The sample proportion is determined by dividing the sample's success rate by the sample size.
The sample must be representative of the population for it to be a reliable point estimate of the population proportion. To accurately reflect the proportions of various groups or categories present in the population, the sample should be chosen at random.
Learn more about population:https://brainly.com/question/30324262
#SPJ1
Given the side length a=9 and the angle B=46∘ on the triangle below, find the lengths of b and c and the measure of angle A. Do not round during your calculations, but round your final answers to one decimal place.

Answers
well, since all interior angles in a triangle add up to 180°, by definition A = 44°, since B and A are complementary anyway.
\(\cos(46^o )=\cfrac{\stackrel{adjacent}{9}}{\underset{hypotenuse}{c}}\implies c=\cfrac{9}{\cos(46^o)}\implies c\approx 13.0 \\\\[-0.35em] ~\dotfill\\\\ \tan(46^o )=\cfrac{\stackrel{opposite}{b}}{\underset{adjacent}{9}}\implies 9\tan(46^o )=b\implies 9.3\approx b\)
Make sure your calculator is in Degree mode.
Alice and Bob each have a certain amount of money. If Alice receives n dollars from Bob, then she will have 7 times as much money as Bob. If, on the other hand, she gives n dollars to Bob, then she will have 2 times as much money as Bob. If neither gives the other any money, what is the ratio of the amount of money Alice has to the amount Bob has?
Answers
The ratio of the amount of money Alice has to the amount Bob has is approximately 3.36 : 1.
How to find the ratio of money ?According to the problem, two equations can be set up:
If Alice receives n dollars from Bob, then she will have 7 times as much money as Bob. This gives us the equation:
A + n = 7(B - n)
If Alice gives n dollars to Bob, then she will have 2 times as much money as Bob. This gives us the second equation:
A - n = 2(B + n)
We can rearrange these equations to make them easier to solve:
8n = 7B - A
3n = A - 2B
Setting these equal to each other, since they are both equal to 24n, gives:
21B - 3A = 8A - 16B
37B = 11A
A / B = 37 / 11
= 3. 36
Find out more on ratio at https://brainly.com/question/31414597
#SPJ1
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
After taking your Freshman English class, you notice there is quite a difference between the students in the classes related to your Business major and your general education requirements. You believe it comes down to a difference in verbal and math abilities. You are interested in seeing how your English classmates performed on two parts of the SAT. You randomly collect data from 28 students on their Math SAT score (population
1), and randomly select another 25 students and collect data on their Verbal SAT score (population
2). After entering the data into Excel you obtain the following output: t-Test: Two-Sample Assuming Unequal Variances Q=0.05 Math SAT Verbal SAT Mean 668. 7604 701.888 Variance 3826.406 6944.827 Observations 28 25 Hypothesized Mean Difference 0 df 44 t Stat P(T<=t) one-tail t Critical one-tail 1.68 P(T<=t) two-tail t Critical two-tail 2.01 What is the value of the test statistic to test if math and verbal scores differ in the SAT exam?
a. -1.479
b. There is not enough information to answer this question
C. -1.627
d. 30.116
e. 30.116
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
The correct option is C
Step-by-step explanation:
From the question we are told that
The sample size for Math SAT is \(n_1 = 28\)
The sample size for Verbal SAT is \(n_2 = 25\)
Generally the test statistics is mathematically represented as
\(t = \frac{\mu_1 - \mu_2}{ \sqrt{\frac{\sigma^2_1 }{n_1} + \frac{\sigma_2^2}{n_2} } }\)
substituting 668. 7604 for \( \mu_1\) , 701.888 for \( \mu_2\), 3826.406 for \( \sigma_1^2\) , 6944.827 for \(\sigma_2^2\)
So
\(t = \frac{668.7604 - 701.888}{ \sqrt{\frac{3826.406}{28} + \frac{6944.827}{25} } }\)
=> \(t = 1.627\)

The number of years, y a person in Japan is expected to live can be approximated by the equation y = 0.28x + 73, wher x is the number of years since 1970
Answers
The number of years that a person in Japan is expected to live based on the equation will be 87 years.
The equation given in the question is represented as: y = 0.28x + 73.
Since x is the number of years since 1970, using 2021 as an illustration, then x will be:
= 2021 - 1970 = 51
Therefore, putting the value of x back into the equation will be:
y = 0.28x + 73.
y = 0.28(51) + 73
y = 14.28 + 73
y = 87.28
Therefore, the life expectancy is 87 years.
Read related link on:
https://brainly.com/question/25307849
Help pleaseeeeeeeeeeeeee

Answers
Answer: f(8) = 620.6
Step-by-step explanation:
To solve, you must first use substitution, and replace the x value in the given function, with 8.
\(f(8)=\frac{750}{1 + 74e^{-0.734(8)} }\)
Next you follow PEMDAS to solve the rest of the equation to find f(8).
What is PEMDAS?
PEMDAS is the order of operations for mathematical expressions involving more than one operation.
You solve in the following order
P = ParenthesisE = ExponentsM = MultiplicationD = DivisionA = AdditionS = SubtractionIn this case our next step is deal with the exponents.
And by doing so, you will be multiplying -0.734 by 8
\(f(8)=\frac{750}{1 + 74e^{-5.872} }\)
And typical with exponents we would raise the number or variable given to the power of the exponent.
However we have a continuous number in this case, which is e.
What is e?
e is a mathematical constant approximately equal to 2.71828
We can now use a calculator to find what e (2.71....) is when raise to the exponent -5.872. Which results to 0.002817 (0.0028172332293320237716146943697).
When continuing to use numbers in calculators, don't use the rounded or shortened of the full number. Make sure to use the all of the numbers (given in the calculator) to its full extent to maintain accuracy.
\(f(8)=\frac{750}{1 + 74(0.002817) }\)
Now multiply 74 and 0.002817.... (use the full number to multiply (0.0028172332293320237716146943697)). The product is (0.2084752589705697590994873833578).
\(f(8)=\frac{750}{1 + 0.2084 }\)
Now lets add 1 + 0.2084.... and you get 1.2084
\(f(8)=\frac{750}{1.2084 }\)
Last you need to divide:
and you get that
f(8) = 620.6167
Now lets go back to the question, and we see that is says for you to round your answer to the nearest tenth.
so your final answer is:
f(8) = 620.6
Which system of linear equations appears to have a solution of (3,0)?
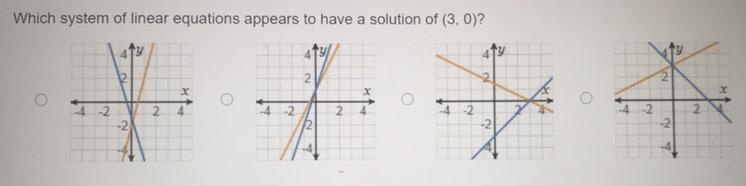
Answers
Answer:
C
Step-by-step explanation:
If C(x) is the cost of producing x units of a commodity, then the average cost per unit is c(x) = C(x)/x. Consider the cost function C(x) given below.
C(x) = 54,000 + 240x + 4x^3/2
Required:
a. Find the total cost at a production level of 1000 units.
b. Find the average cost at a production level of 1000 units.
c. Find the marginal cost at a production level of 1000 units.
d. Find the production level that will minimize the average cost.
e. What is the minimum average cost?
Answers
Answer:
a. C(1,000) = 420,491.11
b. c(1,000) = 420.49
c. dC/dx(1,000) = 429.72
d. x = 900
e. c(900) = 420
Step-by-step explanation:
We have a cost function for x units written as:
\(C(x) = 54,000 + 240x + 4x^{3/2}\)
a. The total cost for x=1000 units is:
\(C(1,000) = 54,000 + 240(1,000) + 4(1,000)^{3/2}\\\\C(1,000)=54,000+240,000+4\cdot 31,622.78\\\\C(1,000)=54,000+240,000+ 126,491.11 \\\\C(1,000)= 420,491.11\)
b. The average cost c(x) can be calculated dividing the total cost by the amount of units:
\(c(1,000)=\dfrac{C(1,000)}{1,000}=\dfrac{ 420,491.11 }{1,000}= 420.49\)
c. The marginal cost can be calculated as the first derivative of the cost function:
\(\dfrac{dC}{dx}=240(1)+4(3/2)x^{3/2-1}=240+6x^{1/2}\\\\\\\dfrac{dC}{dx}(1,000)=240+6(1,000)^{1/2}=240+6\cdot 31.62=429.72\)
d. This value for x, that minimizes the average cost, happens when the first derivative of the average cost is equal to 0.
\(c(x)=\dfrac{C(x)}{x}=\dfrac{54,000+240x+4x^{3/2}}{x}=54,000x^{-1}+240+4x^{1/2}\\\\\\ \dfrac{dc}{dx}=54,000(-1)x^{-2}+0+4(1/2)x^{-1/2}=0\\\\\\\dfrac{dc}{dx}=-54,000x^{-2}+2x^{-1/2}=0\\\\\\2x^{-1/2}=54,000x^{-2}\\\\\\x^{-1/2+2}=54,000/2=27,000\\\\\\x^{3/2}=27,000\\\\\\x=27,000^{2/3}=900\)
e. The minimum average cost is:
\(c(900)=54,000(900)^{-1}+240+4(900)^{1/2}\\\\c(900)=60+240+120\\\\c(900)=420\)
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
The manufacturer of a soccer ball claims that only 3% of the soccer balls produced are faulty. An employee of this company examines the long-run relative frequency of faulty soccer balls produced as shown in the graph.
A graph titled Faulty Soccer Balls has frequency on the x-axis, and probability on the y-axis. The graph levels out around y = 0.06.
Which conclusion can be drawn from this graph?
The company’s claim seems to be true because the graph shows that when 50 soccer balls were tested, only about 3% of them were faulty.
We should not believe the company’s claim that only 3% of their soccer balls are faulty because this graph shows a continuous increase in probability.
Because the graph shows that the probability of producing a faulty soccer ball is 0.03, we can believe the company’s claim that only 3% of the produced soccer balls are faulty
The graph shows that the probability of producing a faulty soccer ball is about 0.06; therefore, we should not believe the company’s claim that only 3% of the produced soccer balls are faulty.
Answers
Answer:
The answer is D
Step-by-step explanation:
Answer:
D. The graph shows that the probability of producing a faulty soccer ball is about 0.06; therefore, we should not believe the company’s claim that only 3% of the produced soccer balls are faulty.
Step-by-step explanation:
A solid figure is composed of a cube and a right triangular
prism. The figure and some of its dimensions are shown in
this diagram.
- 8 cm
What is the volume of the figure?
A
6 cm
B
560 cubic centimeters
704 cubic centimeters
C 728 cubic centimeters

Answers
Answer:
Option B
Step-by-step explanation:
704 cubic centimeters
Jason is buying wings and hot dogs for a party. One package of wings costs $7. Hot dogs cost $5 per package. He must spend no more than $40. Write and inequality to represent the cost of Jason’s food for the party. Jason knows that he will be buying at least 5 packages of hot dogs. Write an inequality to represent this situation. Graph both inequalities. Give two options for Jason when buying wings and hot dogs.
Answers
An inequality to represent the cost of Jason’s food for the party is
An inequality to represent this situation "Jason knows that he will be buying at least 5 packages of hot dogs" is
The two options for buying wings and hot dogs include the following:
One (1) package of wings and five (5) packages of hot dogs.Two (2) packages of wings and five (5) packages of hot dogs.How to write the required system of linear inequalities?In order to write a system of linear inequalities to describe this situation, we would assign variables to the number of packages of hot dogs and number of packages of wings respectively, and then translate the word problem into algebraic equation as follows:
Let the variable x represent the number of packages of wings.Let the variable y represent the number of packages of hot dogs.Since one package of wings costs $7 and Hot dogs cost $5 per package, and he must spend no more than $40, a linear inequality which represents this situation is given by;
7x + 5y ≤ 40
Additionally, since Jason knew he would buy at least 5 packages of hot dogs, a linear inequality which represents this situation is given by;
y ≥ 5
Next, we would use an online graphing calculator to plot the above system of linear inequalities as shown in the graph attached below.
Read more on inequality here: brainly.com/question/29115398
#SPJ1

.....................help

Answers
9514 1404 393
Answer:
-0004.00
Step-by-step explanation:
The segment has a "rise" of -4 units for the "run" of 1 unit between x=2 and x=3. Then the slope is ...
slope = rise/run = -4/1 = -4
A baseball player gets 18 hits in the first 21 games of the season. If he continues hitting at the same rate, how many hits will he get in the first 28 games?
In the first 28 games, he'll get how many hits.
Answers
Answer:
126
Step-by-step explanation: I am pretty sure this is right so my explanation for this answer is, I subtracted 28 by 21 to see how many games were left, I got 7. So then I multiplyed 18 by 7 to see the total of each to have the final answer.
(sorry if wrong)
one antifreeze solution is 41% alcohol and another is 24% alcohol. how much of each mixture should be added to make 51 l of a solution that is 35% alcohol.
Answers
Jean is working out the total cost for her new mobile phone plan with an 18 month contract. The provider charges an initial connection fee of $75. The plan costs $25 a month for the first six months, and then $35 a month for the remaining 12 months. How much will Wendy pay in total for her 18 month contract?
Answers
Answer: $35x 12= $420 so that's for the remaining 12 months. $420+ 75=$495. The next step is to multiply $25 and 6. $25x6= $150.
$495+$150= $645 per month.
Step-by-step explanation:
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qBCO5ypO9m13MpdV66LMvZB6FUp8SIQM.png)
Answers
The reasoning presented lacks explicit explanations and logical connections between the steps, making it difficult to fully understand the intended proof strategy.
The given proof aims to show that the Separation Axioms can be derived from the Replacement Schema using a particular construction involving a formula p(x, y). Let's analyze the proof step by step:
Define the formula p(x, y) as x = yo(x).
This formula states that for each x, y pair, x is equal to the unique object y such that y is obtained by applying the operation o to x.
Define the set F as {(x, x) (x)}.
This set F contains pairs (x, x) where x is the unique object obtained by applying the operation (x) to x.
Claim: F(X) = {y (x = X)p(x, y)} = {y: (x = X)x = y^o(x)} = {x: (3x € X)o(x)} = {x X: (x)}.
This claim asserts that F(X) is equivalent to {y (x = X)p(x, y)}, which is further equivalent to {y: (x = X)x = y^o(x)}, and so on.
The proof states that since (x, y) satisfies the functional formula VaVyVz(p(x, y)^(x, z) y = z), it follows that (x, y) is a functional formula.This step emphasizes that the formula p(x, y) satisfies certain properties that make it a functional formula, which is relevant for the subsequent deductions.
Finally, the proof concludes that the Separation Axioms follow from the Replacement Schema, based on the previous steps.
For more such questions on explicit
https://brainly.com/question/30394385
#SPJ8
