Find any points on the hyperboloid x² - y² - z² = 4 where the tangent plane is parallel to the plane z = 8x + 8y. (If an answer does not exist, enter DNE.) (x, y, z) =
Answers
To find any points on the hyperboloid x² - y² - z² = 4 where the tangent plane is parallel to the plane z = 8x + 8y, we first need to find the gradient of the hyperboloid at any point (x, y, z) on the surface.
The gradient of the hyperboloid is given by (∂f/∂x, ∂f/∂y, ∂f/∂z), where f(x, y, z) = x² - y² - z² - 4. Taking partial derivatives with respect to each variable, we get:
∂f/∂x = 2x
∂f/∂y = -2y
∂f/∂z = -2z
So the gradient of the hyperboloid at any point (x, y, z) is (2x, -2y, -2z).
Next, we need to find the equation of the plane that is tangent to the hyperboloid at (x, y, z). This is given by:
2x(x - x0) - 2y(y - y0) - 2z(z - z0) = 0
where (x0, y0, z0) is the point on the hyperboloid where the tangent plane intersects the surface. We can rewrite this equation as:
2x(x0 - x) + 2y(y0 - y) + 2z(z0 - z) = 0
Now we want to find a point (x, y, z) on the hyperboloid where the tangent plane is parallel to the plane z = 8x + 8y. This means that the normal vector to the tangent plane is parallel to the normal vector to the plane z = 8x + 8y, which is (8, 8, -1). So we want to find a point (x, y, z) on the hyperboloid where the gradient vector (2x, -2y, -2z) is parallel to (8, 8, -1).
This gives us the system of equations:
2x = 8k
-2y = 8k
-2z = -k
where k is a constant. Solving for x, y, and z in terms of k, we get:
x = 4k
y = -4k
z = k/2
Substituting these values into the equation of the hyperboloid x² - y² - z² = 4, we get:
(4k)² - (-4k)² - (k/2)² = 4
16k² - 16k² - k²/4 = 4
-15k²/4 = 4
k² = -16/15
Since k² is negative, there is no real solution for k, and therefore no point on the hyperboloid where the tangent plane is parallel to the plane z = 8x + 8y. Therefore, the answer is DNE.
Learn more about hyperboloid, here:
brainly.com/question/31054806
#SPJ11
Related Questions
1.Consider a 64-bit architecture machine where physical memory is 128GB a.If we would like to run processes as big as 256GB how many bits would be required for the logical address? 38 2 9& 25661 b.If we are using pages of size 4KB, how many bits are needed for displacement into a page? 12 bits 4KB= c.If a single level page table is used, what is the maximum number of entries in this table? 38 26 entries d.What is the size of this single level page table in terms of 4KB pages? 2o Pages e. If a two-level page-table is used and the outer page table is an 4KB page,how many entries does it contain, maximally? f. How many bits of the logical address are used to specify an index into the inner page (page of page table)?
Answers
a). 2^38 bytes of memory
b). 12 bits
c). The maximum number of entries in the single-level page table would be 2^38.
d). The size would be 2^38 * 4KB, which equals 2^20 pages.
e). The maximum number of entries it can have depends on the remaining bits of the logical address.
f). The amount of bits required to denote an index into the inner page table is obtained by subtracting the offset and outer page index bits from the logical address.
a. To address a physical memory size of 128GB (2^37 bytes), a 64-bit architecture would require 38 bits for the logical address, allowing access to a maximum of 2^38 bytes of memory.
b. Given that the page size is 4KB (2^12 bytes), 12 bits would be needed to specify the displacement into a page. This means that the lower 12 bits of the logical address would be used for page offset or displacement.
c. With a single-level page table, the maximum number of entries would be equal to the number of possible logical addresses. In this case, since the logical address requires 38 bits, the maximum number of entries in the single-level page table would be 2^38.
d. The size of the single-level page table is determined by the number of entries it contains. Since each entry maps to a page of size 4KB, the size of the single-level page table can be calculated by multiplying the number of entries by the size of each entry. In this case, the size would be 2^38 * 4KB, which equals 2^20 pages.
e. For a two-level page table, the size of the outer page table is determined by the number of entries it can contain. Since the outer page table uses 4KB pages, the maximum number of entries it can have depends on the remaining bits of the logical address. The number of bits used for the index into the outer page table is determined by subtracting the bits used for the inner page index and the offset from the total number of bits in the logical address.
f. The number of bits used to specify an index into the inner page table can be determined by subtracting the bits used for the offset and the bits used for the outer page index from the total number of bits in the logical address. The remaining bits are then used to specify the index into the inner page table.
Learn more about bytes here:
https://brainly.com/question/15166519
#SPJ11
Use the given pair of vectors, v = - i + 6 j and w = 5 j , to find the following quantities.
v ⋅ w
proj w ( v ) = i + j .
the angle θ (in degrees rounded to the nearest hundredth) between v and w degrees
q = v - proj w ( v ) = i + j .
q ⋅ w
Answers
The angle θ (in degrees rounded to the nearest hundredth) between v and w degrees q ⋅ w = 5, To find v ⋅ w, we take the dot product:
v ⋅ w = (-i + 6j) ⋅ (0i + 5j) = 0 - 30 = -30
To find the projection of v onto w, we use the formula:
proj w (v) = (v ⋅ w / ||w||^2) w
First, we need to find ||w||:
||w|| = ||5j|| = 5
Now we can find the projection:
proj w (v) = (-i + 6j) ⋅ (0i + 5j) / 5^2 * 5j = 6/5 j
Note that this is not equal to i + j.
To find the angle θ between v and w, we use the formula:
cos θ = (v ⋅ w) / (||v|| ||w||)
First, we need to find ||v||:
||v|| = ||-i + 6j|| = sqrt((-1)^2 + 6^2) = sqrt(37)
Now we can find the cosine of the angle:
cos θ = (-30) / (sqrt(37) * 5) = -6 / (sqrt(37))
Taking the inverse cosine, we get:
θ ≈ 98.85 degrees (rounded to the nearest hundredth)
To find q, we subtract the projection from v:
q = v - proj w (v) = -i + 6j - 6/5j = -i + 30/5j - 6/5j = i + j
Finally, to find q ⋅ w, we take the dot product:
q ⋅ w = (i + j) ⋅ (0i + 5j) = 5
Therefore, q ⋅ w = 5.
Learn more about dot product
https://brainly.com/question/29097076
#SPJ4
He has hired you as their new production manager. Your job is to look at five different solid figures and determine which would best suit the needs of the company for packaging the candy. You will choose one of the five options shown below. The candy is animal gummies. The package must hold between 60 and 70 cubic inches (roughly 4-5 cups of space). The cost of the plastic for the packaging is $0.003 per square inch
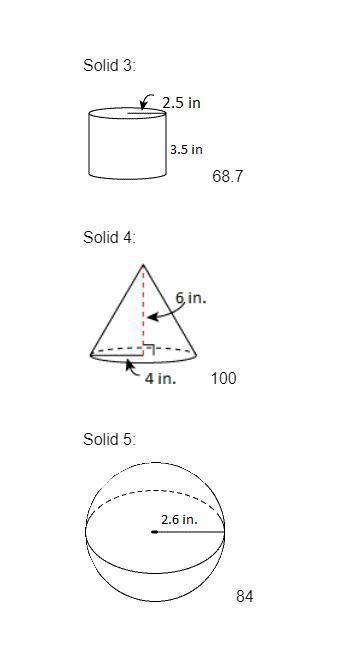


Answers
NEED NOW PLZ 30 POINTS !!!!!!!!!!!!!!!!!!!!!!!!!!!!
What is the area of the trapezoid?
1440 square yards
1512 square yards
1560 square yards
1680 square yards

Answers
Step-by-step explanation:
A=
\( \frac{a + b}{2} h\)
So :
\(area \: = \frac{36 + 42}{2} \times 40 \\ \frac{78}{2} \times 40 = 39 \times 40 = 1560\)
A machine costs Rs. 480. It is sold at a profit of 40%. What is the selling price
Answers
Answer:
672
Step-by-step explanation:
40% of 480 is 192. Add that to the original price and you get 672
Multiply to find the product.
64.7 x 28 = ______
Answers
Answer:
1811.6
Step-by-step explanation:
647x28
18116
move once to the left bc of the point in 64.7
1811.6
64.7 * 28 = 1811.6!
hope this helps :p
in herrnstein's matching equation, the letters and numbers to the left of the equals sign refer to what?
Answers
In Herrnstein's matching equation, the letters and numbers to the left of the equals sign refer to behaviour.
THE MATCHING LAW
Herrnstein's Experiment Herrnstein (1961) conducted an experiment with pigeons in a room with two response buttons, red and white. Each key was assigned its own VI gain schedule. For example, under one condition, the left button pick was boosted on a VI 135 second schedule, and the right button pick was boosted on a VI 270 second schedule.
After the birds have learned as much as possible about this electoral situation, how do they distribute their responses? We trained them for days and then measured their reactions. As is often the case with VI schedules, birds returned many responses for each reinforcer received. Most interesting, however, is that in this condition, where two-thirds of the reinforcers came from the left button, the birds performed about two-thirds of the responses with the left button. That is, the proportion of left button responses equaled or matched the proportion of reinforcers delivered by the left button. In another condition, two birds received only about 15% of reinforcers from the left key and responded about 15% to that key.
Based on these results, Herrnstein proposed the following general principle for individual behavior when presented with alternative sequences. So, what you think makes sense rather than other options available at that particular moment.
To learn more about Matching law, refer:
https://brainly.com/question/15875828
#SPJ4
Sarah and her children went into a movie theater where they sell bags of popcorn for $7.50 each and drinks for $4.50 each. Sarah has $90 to spend and must buy a minimum of 16 bags of popcorn and drinks altogether. If xx represents the number of bags of popcorn purchased and yy represents the number of drinks purchased, write and solve a system of inequalities graphically and determine one possible solution.
Answers
Answer:
A possible solution is she should by 6 bags of popcorn and 10 drinks
Step-by-step explanation:
The price of each bag of popcorn = $7.50
The price of each drink = $4.50
The amount Sarah has to spend = $90
The number of bags of popcorn and drinks Sarah must buy = 16 bags of popcorn and drinks
Let the number of bags of popcorn purchased be represented by x and the number of drinks purchased be represented by y
Therefore, we have;
x + y ≥ 16.....(1)
x × 7.5 + y × 4.5 ≤ 90
Which gives;
7.5·x + 4.5·y ≤ 90....(2)
Rewriting the inequalities as a function of y, gives;
From inequality (1), x + y ≥ 16, we have;
y = ≥ 16 - x
From inequality (2), 7.5·x + 4.5·y ≤ 90, we have;
7.5·x + 4.5·y ≤ 90
4.5·y ≤ 90 - 7.5·x
y ≤ 90/4.5 - 7.5/4.5·x
y ≤ 20 - 5/3·x
Please find attached, the plot of the inequalities
A possible solution is given as the value of x = 6, where y = 10
Therefore, she should by 6 bags of popcorn and 10 drinks.

PLEASE ANSWER (100points)
When evaluating (6 x + 9) squared minus 5 for x = 1, the given value of 1 is substituted for what part of the expression?
the exponent
the constant
the variable
any numerical value
Answers
Answer:
the variable
Step-by-step explanation:
Given expression:
\((6x+9)^2-5\)
When evaluating the expression for \(x=1\), we need substitute 1 for the variable (\(x\)) in the expression.
Evaluating the expression for \(x=1\):
\(\implies (6\cdot1+9)^2-5\)
\(\implies (6+9)^2-5\)
\(\implies (15)^2-5\)
\(\implies 225-5\)
\(\implies 220\)
Answer:
Variable
As variable is x and we have to substitute x=1Step-by-step explanation:
Let's find the value
\(\\ \rm\Rrightarrow (6x+9)^2-5\)
\(\\ \rm\Rrightarrow (6+9)^2-5\)
\(\\ \rm\Rrightarrow 14^2-5\)
\(\\ \rm\Rrightarrow 196-5\)
\(\\ \rm\Rrightarrow 191\)
5. For which values of x and y is line p parallel to line q? (1 point)
R
(26y)⁰
Ox= 5, y = 3
Ox= 1, y = 5
Ox=3, y=5
Ox=3, y=6
(16x + 2)°
(45x-51

Answers
Answer:
x = 3 and y = 5
Step-by-step explanation:
1st: The sum of the same side interior angles equal 180°. Use this to solve for x.
45x - 5 + 16x + 2 = 180
61x - 3 = 180
61x - 3 + 3 = 180 + 3
61x/61 = 183/61
x = 3
2nd: find the measure of angle 16x + 2
16x + 2
16(3) + 2
48 + 2
50°
3rd: the sum of the 50° angle and the angle 26y° is 180 since they make a straight angle. Make an equation and solve for y.
50 + 26y = 180
50 - 50 + 26y = 180 - 50
26y = 130
26y/26 =130/26
y = 5
what is the probability of coming up with the correct unscrambling through random letter selection?
Answers
the probability of randomly selecting the correct unscrambling would be 1/n!. As the length of the word increases, the probability of randomly selecting the correct unscrambling becomes increasingly small due to the exponential growth of possible arrangements.
The probability of coming up with the correct unscrambling through random letter selection depends on the specific word being unscrambled and the number of possible permutations. In general, the probability can be quite low due to the large number of possible combinations.
To calculate the probability, you would need to know the total number of possible letter arrangements and the number of arrangements that result in the correct unscrambling. Let's assume we have a word with n letters. The total number of possible arrangements is n!, which represents n factorial (the product of all positive integers from 1 to n).
The number of arrangements that result in the correct unscrambling depends on the specific word and the length of the word. For example, if the word has 4 letters, there are 24 possible arrangements (4!). However, only one of those arrangements is the correct unscrambling.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Don’t mind wat I clicked I don’t know if it’s right but please help

Answers
Answer:
y = 5x
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
For every 1 the x goes right, the y goes up 5
Which is the variable in this equation ?
3v - 2 = 10
answer is on the pic.

Answers
Answer:
The variable is v
Step-by-step explanation:
Evaluar expresiones Evalúa a 4 cuando a 7.
Answers
The value of the expression a + 4 when a = 7 is 11.
What is Algebra?
Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
We are given that;
Function= a+4
Now,
By algebra
If a = 7, then we can substitute this value into the expression a + 4 to get:
=a + 4
= 7 + 4
= 11
Therefore, by algebra the answer will be 11.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1
The complete question is;
Evaluate the expression a+4 when a=7?
Use the Heun method to approximate y(2.6) after two steps, where y(t) is the solution of the IVP { y' = (t - 1)(y + 2) y(2) =1, }
Draw the approximate solution curve.
Answers
The given initial value problem is:y' = (t - 1)(y + 2), y(2) = 1.
We are to apply the Heun method to approximate y(2.6) after two steps.
SolutionWe first need to obtain the step size. We are taking two steps to reach t = 2.6. Thus, our step size ish = (2.6 - 2)/2 = 0.3.
Now, we apply the Heun method:Step 1t0 = 2, y0 = 1t1 = 2 + h = 2.3The slope at (2, 1) is:f(t0, y0) = (t0 - 1)(y0 + 2) = (2 - 1)(1 + 2) = 3The slope at (t1, w1) is:f(t1, w1) = (t1 - 1)(w1 + 2), where w1 is the intermediate value obtained as:w1 = y0 + hf(t0, y0) = 1 + 0.3(3) = 1.9Thus, f(t1, w1) = (2.3 - 1)(1.9 + 2) = 3.9Using the average slope, we estimate the value of y at t1:y1* = y0 + h[f(t0, y0) + f(t1, w1)]/2= 1 + 0.3[3 + 3.9]/2 = 2.085Step 2t2 = 2.3 + h = 2.6The slope at (t1, y1*) is:f(t1, y1*) = (t1 - 1)(y1* + 2) = (2.3 - 1)(2.085 + 2) = 3.417The slope at (t2, w2) is:f(t2, w2), where w2 is the intermediate value obtained as:w2 = y1* + hf(t1, y1*) = 2.085 + 0.3(3.417) = 3.118Thus, f(t2, w2) = (2.6 - 1)(3.118 + 2) = 7.555.
Using the average slope, we estimate the value of y at t2:y2* = y1* + h[f(t1, y1*) + f(t2, w2)]/2= 2.085 + 0.3[3.417 + 7.555]/2 = 3.411
Finally, we obtain the approximate solution curve as follows:
We take t = 2 and y = 1 as the initial point on the solution curve. Using the Heun method, we obtain the second point on the curve as (2.3, 2.085). We then use this point as the initial point to obtain the third point on the curve as (2.6, 3.411). Thus, the approximate solution curve is the line segment connecting the three points:(2, 1), (2.3, 2.085), and (2.6, 3.411).
The approximate value of $y(2.6)$ after two steps is $y_2 \approx 3.5852$, The Heun method is a method for numerically integrating ordinary differential equations (ODEs).
It is a second-order Runge-Kutta method that uses the average of two estimates of the slope at each time step. The method can be written as follows:$$\begin{aligned} k_1 &= f(t_n,y_n) \\ k_2 &= f(t_n + \Delta t, y_n + \Delta t k_1) \\ y_{n+1} &= y_n + \frac{1}{2}(k_1 + k_2)\Delta t \end{aligned}$$Here, $f(t,y)$ is the right-hand side of the ODE, $y_n$ is the approximate value of $y(t)$ at time $t_n$, and $\Delta t$ is the time step.
To approximate $y(2.6)$ after two steps using the Heun method, we need to take two steps of size $\Delta t = 0.3$ from $t = 2$ to $t = 2.6$. The values of $y$ at the end of each step are computed as follows
To know more about differential equations visit:-
https://brainly.com/question/25731911
#SPJ11
A bag contains 75 marbles some red some blue the ratio of red marbles to blue marbles is 3 to 2 how many red marbles are there
Answers
Answer: 45 red marbles
Step-by-step explanation:
Using the ratios, we can create a fraction for the number of marbles.
3/5 of the bag would be red marbles, and 2/5 of the bag would be blue marbles.
(you get the 5 from adding 3+2 together)
If you take 3/5 of 75, you would get 45 red marbles.
please help with this question and determine a,b,c,d and e

Answers
Answer:
a=7
b=8
c=12
d=33
find e by adding up all numbers in the Venn diagram then subtract the total amount of people by total from the Venn diagram to find e
a video game sells for 79.99 it is marked down 30% what is the sale price on the video game
Answers
You have 1200 feet of fencing and you want to make two fenced in enclosures by splitting one enclosure in
half. What are the largest dimensions of this enclosure that you could build?
Answers
Let x = length and y = width
You would have 2 lengths, so 2x and 3 widths, so 3y
Those need to equal total length of fence:
2x + 3y = 1200
The 3 widths would equal total fence minus the 2 lengths:
3Y = 1200-2x
Solve for y: y = 400 -2/3x
Area = length x width = xy. Replace y :
Area = x(400-2/3x) = 400x-2/3x^2
Differentiate:
400-4x/3 =0
4x/3 = 400
4x = 1200
X = 300
Y = 400-2/3(300) = 200
The dimension would be 300 ft x 200 ft
HELP HELP HELP HELP!!!!!!!!!!!!

Answers
Answer:
y-7 hope it helps your welcome
a software company is interested in improving customer satisfaction rate from the currently claimed. the company sponsored a survey of customers and found that customers were satisfied. what is the test statistic ?
Answers
The test statistic depends on the specific hypothesis test being conducted.
In general, a test statistic is a value calculated from the sample data that is used to assess the likelihood of observing the data under the null hypothesis. It is used to make a decision about whether to reject or fail to reject the null hypothesis. The choice of test statistic depends on the specific hypothesis being tested and the nature of the data.
To determine the test statistic in a given hypothesis test, it is necessary to specify the null hypothesis, the alternative hypothesis, and the appropriate statistical test being used. This information is crucial in calculating the test statistic and interpreting its significance. Without these details, it is not possible to provide a specific test statistic in this context.
Learn more about test statistic here:
https://brainly.com/question/31746962
#SPJ11
The complete question is:
A software company is interested in improving customer satisfaction rate from the 75% currently claimed. The company sponsored a survey of 152 customers and found that 120 customers were satisfied. What is the test statistic z?
Doug is a salesperson in a retail store and earns $75 per week plus 15% of his weekly sales. If Doug makes $555 one week, what are his sales that week?
Answers
The sales that Doug makes in the week is $3200.
How to calculate the sales?From the information illustrated, Doug is a salesperson in a retail store and earns $75 per week plus 15% of his weekly sales and Doug makes $555 one week.
Let the sales be represented by x.
Based on the information, this will be:.
75 + (15% × x) = 555
75 + 0.15x = 555
Collect like terms
0.15x = 555 - 75
0.15x = 480
Divide
x = 480 / 0.15
x = 3200
The sales is $3200.
Learn more about percentages on:
brainly.com/question/24877689
#SPJ1
Solve the following expression 8 + (-20)
Answers
Answer:
-12
Step-by-step explanation:
integer rule = when a + and - comes it is indicated as - so ..
8-20 = -12
we put a minus sighnbecause 20 is the bigger number
Answer:
-12
Step-by-step explanation:
Note the rules of the signs:
If there are two positive signs next to each other, the resulting sign will be positive. Example + (+ ).
If there is one negative sign and one positive sign directly next to each other, the resulting sign will be negative Example - (+ ) or + (- ).
If there are two negative signs directly next to each other, the resulting sign will be positive. Example - (- ).
In this case, there is one negative, and one positive sign. Subtract 8 with 20:
8 + (-20) = 8 - 20 = -12
-12 is your answer.
~
In the diagram, what is the measure of angle 1?

Answers
Answer:
C
Step-by-step explanation:
The adjacent angle to the left of 9x is 180 - 9x ( straight angle )
180 - 9x and 3x are corresponding angles and are congruent , then
3x = 180 - 9x ( add 9x to both sides )
12x = 180 ( divide both sides by 12 )
x = 15
Then
∠ 1 and 180 - 9x are vertically opposite angles and are congruent, so
∠ 1 = 180 - 9(15) = 180 - 135 = 45° → C
if tan (x+y)=4/3 and tan x=5/13. evaluate tan y
Answers
tan(x + y) = (tan x + tan y) / (1 - tan x * tan y)
Substituting the given values, we get:
4/3 = (5/13 + tan y) / (1 - 5/13 * tan y)
Multiplying both sides by the denominator and simplifying, we get:
52/3 - 20/3 * tan y = 5/13 + tan y
Multiplying both sides by 3/20 and simplifying, we get:
tan y = (52/3 - 5/13) / (20/3 + 1)
tan y = (1699/39) / (23/3)
tan y = 221/299
Therefore, tan y is approximately 0.7391 (rounded to four decimal places).
Morgan worked for three weeks during the summer earning money
on Mondays, Tuesdays, Wednesdays, Thursdays and Fridays. The
following matrix represents his earnings.
24 22 32
25 28 30
30 28 32
10 15 19
35 32 30
How much money did Morgan make in the first week?
Answers
The amount of money that Morgan was able to make in the first week would be $ 124
How to find the earnings with matrices ?Matrices are mathematical objects which have a rectangular array of numbers, symbols, or expressions laid out in rows and columns. Each element is identified by its row and column location inside the matrix.
The columns have five entries which means that this must be the amount earned per day of a week. The first week earnings would therefore be:
= 24 + 25 + 30 + 10 + 35
= $ 124
Find out more on earnings at https://brainly.com/question/15218394
#SPJ1
May I ples have a little help pless
Simplify using the laws of exponents
[2^4/2^ 3]^5
Answers
\(\left[\dfrac{2^4}{2^3} \right]^5 \\\\\\=[2^{4-3}]^5\\\\=[2^1]^5\\\\=2^5\\\\=32\)
.When developing groups, there will almost always be disagreements and conflicts as members work to develop a common understanding. This stage of group development is called○ forming.○ norming.○ performing.○ storming.○ adjourning.
Answers
The stage of group development that is characterized by disagreements and conflicts is called storming. During this stage, group members may have different ideas and opinions about how to approach tasks and goals, and they may struggle to find a common understanding.
Conflict can arise as individuals compete for leadership roles or try to assert their ideas over others. However, this stage is important for groups to progress towards their goals as it allows for open communication and the airing of different perspectives. Eventually, through negotiation and compromise, groups move on to the norming stage where a common understanding is established and roles are defined. From there, groups move on to performing, where they are able to work together effectively towards their goals.
Finally, the adjourning stage is where the group disbands after reaching their goals or completing their tasks.
To know more about Development visit :
https://brainly.com/question/14869932
#SPJ11
The point P(3,5) is rotated 180 degrees CW about the point A(3,2) and then rotated 90 degrees CCW about point B(1,1). What is the coordinate of P after the rotations?
Answers
To determine the coordinate of point P after the described rotations, let's go step by step.
First, the point P(3, 5) is rotated 180 degrees clockwise about the point A(3, 2). To perform this rotation, we need to find the vector between the center of rotation (A) and the point being rotated (P). We can then apply the rotation matrix to obtain the new position.
Let \(\vec{AP}\) be the vector from A to P. We can calculate it as follows:
\(\vec{AP} = \begin{bmatrix} 3 \\ 5 \end{bmatrix} - \begin{bmatrix} 3 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}\).
Now, we can apply the rotation matrix for a 180-degree clockwise rotation:
\(\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\),
where \(\theta\) is the angle of rotation in radians. Since we want to rotate 180 degrees, we have \(\theta = \pi\).
Applying the rotation matrix, we get:
\(\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos(\pi) & -\sin(\pi) \\ \sin(\pi) & \cos(\pi) \end{bmatrix} \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \begin{bmatrix} 0 \\ -3 \end{bmatrix}\).
The new position of P after the first rotation is P'(0, -3).
Next, we need to rotate P' (0, -3) 90 degrees counterclockwise about the point B(1, 1).
Again, we calculate the vector from B to P', denoted as \(\vec{BP'}\):
\(\vec{BP'} = \begin{bmatrix} 0 \\ -3 \end{bmatrix} - \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 \\ -4 \end{bmatrix}\).
Using the rotation matrix, we rotate \(\vec{BP'}\) by 90 degrees counterclockwise:
\(\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix}\),
where \(\theta\) is the angle of rotation in radians. Since we want to rotate 90 degrees counterclockwise, we have \(\theta = \frac{\pi}{2}\).
Using the rotation matrix, we get:
\(\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} \cos \left(\frac{\pi}{2}\right) & -\sin\left(\frac{\pi}{2}\right) \\ \sin\left(\frac{\pi}{2}\right) & \cos\left(\frac{\pi}{2}\right) \end{bmatrix} \begin{bmatrix} -1 \\ -4 \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0\end{bmatrix} \begin{bmatrix} -1 \\ -4 \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \end{bmatrix}\).
The final position of P after both rotations is P''(4, -1).
Therefore, the coordinate of point P after the rotations is (4, -1).
Two lines that form a right angle at their point of intersection.A. PointB. Perpendicular Lines.C. Line.D. Collinear points.
Answers
Option B "Perpendicular Lines" is correct.
"Perpendicular Lines" are two lines that intersect at a right angle, forming 90-degree angles between them. Thus, Option B holds the truth.
Perpendicular lines are a fundamental concept in geometry and they are defined as two lines that meet at a right angle; forming four 90-degree angles. This means that the slopes of the two lines are negative reciprocals of each other. Perpendicular lines are important in many areas of mathematics and physics because they allow us to calculate angles, distances and other geometric properties.
Perpendicular lines are useful in many practical applications such as: architecture, engineering and construction. By understanding the properties of perpendicular lines, one can better understand the geometry of our world and solve real-world problems.
Learn more about Perpendicular lines brainly.com/question/1202004
#SPJ4