Find the height of the trapezoid. A trapezoid. The base lengths are 12 meters and 8 meters. The area is 70 square meters.
Answers
1/2(12+8)h=70
1/2(20)h=70
10h=70
70/10=7
h=7
Related Questions
Statistics
Ethan repairs household appliances such as dishwashers and refrigerators. For each visit, he charges $25 plus $20 per hour of work. A linear equation that expresses the total amount of money Ethan earns per visit is y = 25 + 20x. What are the independent and dependent variables? What is the y-intercept, and what is the slope? Interpret them using complete sentences.
Answers
Answer my geometry plsss

Answers
1) ABCD is a parallelogram (given)
2) \(\overline{BC} \parallel \overline{AD}, \overline{AB} \parallel \overline{CD}\) (opposite sides of a parallelogram are parallel)
3) \(\angle BCA \cong \angle CAD, \angle BAC \cong \angle ACD\) (alternate interior angles theorem)
4) \(\angle A \cong \angle C, \angle B \cong \angle D\) (congruent angles added to congruent angles form congruent angles)
Which equation best represents the relationship between x and y in the graph? A) y = - 3 4 x - 3 B) y = - 4 3 x - 3 C) y = - 3 4 x - 4 D) y = - 4 3 x - 4
Answers
=
14
,
⇒
the length of each leg
=
14
√
2
=
7
√
2
Check :
(
7
√
2
)
2
+
(
7
√
2
)
2
=
196
=
14
2
(OK)
Which of the following is a counterexample to the given statement?
The name of every month ends in the letter y.
a. January
b. July
C February
d. December
Answers
The name of every month ends in the letter y is the given statement. February is a counterexample to this statement. This is because February does not end with the letter 'y'. So the right option is (c) February.
What is a counterexample?
In mathematics, a counterexample is an example that opposes or disproves a statement, proposition, or theorem. It is a scenario, an instance, or an example that goes against the given statement.
Therefore, a counterexample demonstrates that the given statement is false or invalid.In this case, the statement is: "The name of every month ends in the letter y." We have to find which of the months listed does not end in "y."February is the only month in the options listed that does not end in the letter "y."
Thus, it is a counterexample to the given statement. Therefore, the correct option is C, February.
For more questions on: counterexample
https://brainly.com/question/29197877
#SPJ8
Madison wants to ride her bicycle 27 miles this week. She has already rídden 7 miles.
If she rides for 4 more days, write and solve an equation which can be used to
determine m, the average number of miles she would have to ride each day to meet
her goal
Answers
Answer:
x=5
Step-by-step explanation:
Formulate and substitute:d=4v
Rearrange unknown terms to the left side of the equation: 4x=27-7
Calculate the sum or difference: 4x=20
Divide both sides of the equation by the coefficient of variable: x=20÷4
Calculate the product or quotient: x=5
So the Answer is: x=5
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
indicate which type of statistical analysis you use to answer the following research quesiton. is thre a relationship between the number of sodas consumed each year and the number of cavities formed?
Answers
To answer the research question, "Is there a relationship between the number of sodas consumed each year and the number of cavities formed?" a correlation analysis would be appropriate.
This type of statistical analysis examines the relationship between two variables to determine if there is a linear association between them.
In this case, the two variables are the number of sodas consumed each year and the number of cavities formed.
Correlation analysis measures the strength and direction of the relationship between two variables. The strength of the relationship is determined by the correlation coefficient, which ranges from -1 to +1.
A correlation coefficient of -1 indicates a perfect negative relationship, while a correlation coefficient of +1 indicates a perfect positive relationship. A correlation coefficient of 0 indicates no relationship between the two variables.
In this case, if the correlation coefficient is positive, it would indicate that there is a positive relationship between the number of sodas consumed each year and the number of cavities formed. This means that as the number of sodas consumed increases, the number of cavities formed also increases.
On the other hand, if the correlation coefficient is negative, it would indicate a negative relationship between the two variables, meaning that as the number of sodas consumed increases, the number of cavities formed decreases.
In conclusion, to determine if there is a relationship between the number of sodas consumed each year and the number of cavities formed, a correlation analysis would be appropriate.
This type of analysis would measure the strength and direction of the relationship between the two variables, providing valuable insights into the impact of soda consumption on dental health.
learn more about cavities here :brainly.com/question/20515008
#SPJ11
Steffi is painting her house. She has calculated she needs 40 litres of paint in total. She has decided to mix pink paint. She will need 3 litres of white for every litres of red. How many litres of each colour will she need to buy?
Answers
Answer:
Red=10 Pink=30
Step-by-step explanation:
you said for every litres of red; therefore, you need 3 litres of pink paint. So the steps are like this 3+1(P+R) ........... you need 30 litres pink and 10 litres red
I LITTERALY BEG OF YOU TO HELP ME!!
LMN≅PQR
What is the value of x in degrees?

Answers
Answer: 56
Step-by-step explanation:

18⅔ ÷ ⅔
how many children are there?
Answers
Explanation:
18⅔ ÷ ⅔
= 56/3 ÷ 2/3
= 56/3 x 3/2
= 56/2
=28
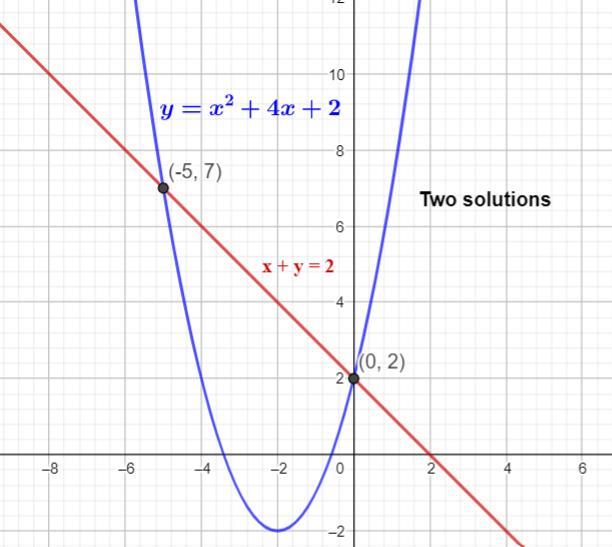
when solving a system of equations that includes one linear equation and one quadratic equation, how many solutions can be found?
Answers
A system of equations with one linear equation and one quadratic equation has "zero or one or two" solutions.
How to solve a system of equations that includes one linear equation and one quadratic equation?Consider a system of equations with one linear equation and one quadratic equation as
Case (1): y = x² + 4x + 2 ...(1)
and x + y = 2 ...(2)
By the substitution method:
from (2), y = 2 - x; Substituting in (1)
⇒ 2 - x = x² + 4x + 2
⇒ x² + 4x + 2 + x - 2 = 0
⇒ x² + 5x = 0
⇒ x(x + 5) = 0
∴ x = 0 and x = -5
If x = 0, then y = 2 - 0 = 2
If x = -5, then y = 2 + 5 = 7
So, the system has two solutions at (0, 2) and (-5, 7).
Case (2): y = x² + 4x + 2 ...(1)
and x - y = 2 ...(2)
By the substitution method:
from (2), y = x - 2; Substituting in (1)
⇒ x - 2 = x² + 4x + 2
⇒ x² + 4x + 2 + 2 - x = 0
⇒ x² + 3x + 4 = 0
we know that b² - 4ac will decide the nature of roots.
So, (3)² - 4(1)(4) = 9 - 16 = -7 < 0
Since the determinant is less than 0, the roots are imaginary. Hence the system has no solution. That means the line and the parabola do not meet.
Case (3): y = x² + 4x + 2 ...(1)
and y = x - 1/4 ...(2)
Substituting (2) in (1), we get
⇒ x - 1/4 = x² + 4x + 2
⇒ x² + 4x + 2 - x + 1/4 = 0
⇒ x² + 3x + 9/4 = 0
⇒ 4x² + 12x + 9 = 0
⇒ (2x + 3)² = 0
⇒ 2x + 3 = 0
∴ x = -3/2
If x = -3/2 then y = -3/4 - 1/4 = -7/4
So, the system has one solution at (-3/2, -7/4).
Therefore, the given type of system has "zero or one or two" solutions.
Learn more about the system of equations here:
brainly.com/question/2376175
#SPJ1


2x = 5y + 8
3x + 2y = 31
Given the above system of equations, what is the value of y?
A. 2
B. 4
C. 6
D. 9

Answers
Answer:
Y is 2
Step-by-step explanation:
First, Solve the equation for the variable y
2y = -3x + 31 : y = -3x/2 + 31/2
Plug this in for variable y in the equation:
2x - 5•(-3x/2+31/2) = 8
19x/2 = 171/2
19x = 171
Solve first equation for the variable x
19x = 171
x = 9
now knowing that x=9, you can plug it into either equation to solve for y.
y = -(3/2)(9)+31/2 = 2
An aluminum gutter in the shape of a trapezoidal prism is to go across the 32-foot front portion of a house. If the two parallel sides of the trapezoid are 6 inches and 9 inches, then how deep in feet must the trapezoid be so that the gutter can hold 10 cubic feet of water? a. 0.5 b. 2.5 c. 6 d. 2
Answers
The depth of the trapezoidal prism needs to be 0.5 feet (a) in order for the gutter to hold 10 cubic feet of water.
To find the depth of the trapezoidal prism, we can use the formula for the volume of a trapezoidal prism, which is given by V = (1/2)h(b1 + b2)L, where V is the volume, h is the depth, b1, and b2 are the lengths of the parallel sides of the trapezoid, and L is the length of the prism.
In this problem, the length of the front portion of the house is given as 32 feet. The two parallel sides of the trapezoid are 6 inches (0.5 feet) and 9 inches (0.75 feet), respectively. We are looking for the depth of the trapezoidal prism that will result in a volume of 10 cubic feet.
Using the formula for volume, we can substitute the given values and solve for h: 10 = (1/2)h(0.5 + 0.75)(32). Simplifying the equation, we get 10 = 41h. Solving for h, we find that h = 10/41 ≈ 0.2439 feet.
Converting the depth to inches, we have approximately 0.2439 * 12 ≈ 2.93 inches. Rounding to the nearest tenth, the depth of the trapezoidal prism should be approximately 0.5 feet or 6 inches to hold 10 cubic feet of water.
Learn more about trapezoidal prism here :
https://brainly.com/question/15301517
#SPJ11
what is an example of a one step equation that would use multiplication
Answers
Answer:
Multiplication equation 6 t = 54 6t = 54 6t=54 Multiply each side by five.
The sum of 2 numbers is 620 the difference is 20
Answers
Answer:
First number is 300 second in 320
Step-by-step explanation:
let x be the first number
let x + 20 be the second
620 = x + (x +20)
620 = 2x + 20
620 - 20 = 2x
600/2 = 2x/2
x= 300
x + 20 = 320
Define variable for each number, sum of the 2 variable must equal 620 then isolate for x and calculate the sum of the first and second number
the numbers are 300 and 320.
You can solve this by using the equation x+ (x+20) = 620.
what does the slope of a beer's law plot represent
Answers
The slope of a beer's law plot represents that one can quantitatively determine the molar absorptivity of a substance, which is essential for accurately determining concentrations of unknown samples using spectrophotometric methods.
In Beer's law, the relationship between the concentration of a substance and its absorbance is described by the equation A = εbc, where A is the absorbance, ε is the molar absorptivity (also known as the molar absorptivity coefficient), b is the path length of the sample, and c is the concentration of the substance.
When plotting a graph of absorbance versus concentration, the slope of the line represents the molar absorptivity (ε). The molar absorptivity is a constant that reflects the substance's ability to absorb light at a specific wavelength. A higher molar absorptivity indicates that the substance has a greater tendency to absorb light and is more sensitive to changes in concentration.
Conversely, a lower molar absorptivity indicates weaker absorption characteristics.
In summary, by measuring the slope of the Beer's law plot, one can quantitatively determine the molar absorptivity of a substance.
To know more about Beer's law, refer here:
https://brainly.com/question/30762062#
#SPJ11
hey could someone please explain and help me please ?

Answers
Answer:
No
Step-by-step explanation:
The inequality k ≥ 10 means "the variable, k, is equal to or more than 10." We are asked if 9 is a solution to the inequality.
The number, nine, is not a solution to this inequality, as 9 is not more than or equal to 10.
Have a lovely rest of your day/night, and good luck with your assignments! ♡
Answer:
No
Step-by-step explanation:
Hello.
The inequality pictured above (k≥10) means that any solution that is greater or equal to 10 fits it. Think of an alligator being the inequality symbol and wants what's bigger. Obviously if k is bigger the alligator wants that over a 10.
In this problem, when 9 is inputted to k, is it bigger or equal then ten?
It is not, which means it is NOT a solution.
Hope this helped!
Use Simpson's Rule and all the data in the following table to estimate the value of the integral ∫ y dx (with boundaries a=-4 and b=2). Here y=f(x) and with values given in the table. x values: -4, -3, -2, -1, 0, 1, 2
y values: -9, -6, -3, 0, 4, 8, 10
The Simpson's Rule approximation =
Answers
The approximation of the integral ∫ y dx using Simpson's Rule and the given data is approximately 3.67.
To estimate the value of the integral ∫ y dx using Simpson's Rule, we need to divide the interval [-4, 2] into subintervals and apply the rule to each subinterval. Simpson's Rule estimates the integral as:
∫ y dx ≈ (h/3) * [f(a) + 4f(a+h) + 2f(a+2h) + 4f(a+3h) + ... + 2f(b-h) + 4f(b-h) + f(b)],
where h is the width of each subinterval, given by h = (b - a) / n, and n is the number of subintervals.
In this case, a = -4, b = 2, and we have 7 data points, so there are 6 subintervals. Let's calculate the approximation:
h = (2 - (-4)) / 6 = 6 / 6 = 1.
Now, let's substitute the given y-values into the Simpson's Rule formula:
∫ y dx ≈ (1/3) * [-9 + 4*(-6) + 2*(-3) + 40 + 24 + 4*8 + 10]
Simplifying:
∫ y dx ≈ (1/3) * [-9 - 24 - 6 + 0 + 8 + 32 + 10]
= (1/3) * [11]
= 11/3
≈ 3.67.
Therefore, the approximation of the integral ∫ y dx using Simpson's Rule and the given data is approximately 3.67.
To know more about subintervals check the below link:
https://brainly.com/question/31405197
#SPJ4
How many subsets does the set T = {salsa, sour cream, queso, guacamole, pico de gallo} have?Question 49 options:a) 5b) 0c) 25d) 32
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
How many subsets does the set T = {salsa, sour cream, queso, guacamole, pico de gallo} have?
Step 2:
The details of the solution are as follows:
Recall that:
The empty set and the set itelf are also part of the subsets that must be included as part of the number of subsets.
If a set has “n” elements,
then the number of subset of the given set is
\(2^n\)Hence, the total number of subsets will be:
\(2^5=\text{ 32 \lparen OPTION D \rparen}\)CONCLUSION:
The final answer is:
\(32\text{ \lparen OPTION D \rparen}\)What is the slope of the line through the points (4, -7) and (9, 2)?
Answers
the answer
y/x so its 9/5
Tom says he is comparing banks to see what interest rates they offer on savings accounts. Explain how Tom should use the information he gets to decide which bank to open a savings account with.
Answers
Tom should choose the bank that gives the highest interest rate on savings accounts
What is interest rate?The amount a lender charges a borrower is called an interest rate, and it is expressed as a percentage of the principal, or the loaned amount. Typically, a loan's interest rate is expressed as an annual percentage rate, or APR.
A savings account or certificate of deposit earnings at a bank or credit union may also be subject to an interest rate (CD). The interest received on these deposit accounts is measured in annual percentage yields. In this case, the one that gives the best rate is the best option to choose.
Learn more about interest on:
https://brainly.com/question/25793394
#SPJ1
Answer:
Tom should choose the bank that offers the highest interest rate on savings accounts. Since the principal and time would be the same for each bank, the higher the interest rate, the more money Tom would earn.
Step-by-step explanation:
this was the sample answer on edge. I hate edge
-2(8f+9)-6n use f=5 and n=7
Answers
Answer: Correct me if I am wrong, but this is how I think you should solve it.
Step-by-step explanation:
1. Simplify 8×5 to 40.
−2×(40+9)−6×7
2. Simplify 40+9 to 49.
−2×49−6×7
3. Simplify −2×49 to −98.
−98−6×7
4. Simplify 6×7 to 42.
−98−42
5. Simplify
−140
Your all done! Hope this helps.
Which sum below has a negative value?
(1) −11+13
(2) −14+6
(3) 23+ -10
(4) 19+-17?
Answers
Answer:
2. -14 + 6
Step-by-step explanation:
-11 + 13 = 2
-14 + 6 = -8
23 + -10 = 13
19 + -17 = 2
Answer:
2.-14+6
if you struggle with adding or subtracting negatives and positives you can look at each number by itself. For example// the number 14 is greater than 6 so you know that because 14 is greater than 6 he product of -14 and positive 6 will be negative.
another example//-11+13, disregard the positive and negative and look at the number itself, 13 is greater than 11. Now look at the sign associated with the number, 13 is positive, because the greater number, 13, is positive the product will also be positive
Step-by-step explanation:
of Use the fourth-order Runge-Kutta subroutine with h=0 25 to approximate the solution to the initial value problem below, at x=1. Using the Taylor method of order 4, the solution to the initia value
Answers
Using the Taylor method of order 4, the solution to the given initial value problem is y(x) = x - x²/2 + x³/6 - x⁴/24 for Runge-Kutta subroutine.
Given initial value problem is,
y' = x - y
y(0) = 1
Using fourth-order Runge-Kutta method with h=0.25, we have:
Using RK4, we get:
k1 = h f(xn, yn) = 0.25(xn - yn)
k2 = h f(xn + h/2, yn + k1/2) = 0.25(xn + 0.125 - yn - 0.0625(xn - yn))
k3 = h f(xn + h/2, yn + k2/2) = 0.25(xn + 0.125 - yn - 0.0625(xn + 0.125 - yn - 0.0625(xn - yn)))
k4 = h f(xn + h, yn + k3) = 0.25(xn + 0.25 - yn - 0.0625(xn + 0.125 - yn - 0.0625(xn + 0.125 - yn - 0.0625(xn - yn))))
y_n+1 = y_n + (k1 + 2k2 + 2k3 + k4)/6
At x = 1,
n = (1-0)/0.25 = 4
y1 = y0 + (k1 + 2k2 + 2k3 + k4)/6
k1 = 0.25(0 - 1) = -0.25
k2 = 0.25(0.125 - (1-0.25*0.25)/2) = -0.2421875
k3 = 0.25(0.125 - (1-0.25*0.125 - 0.0625*(-0.2421875))/2) = -0.243567
k4 = 0.25(0.25 - (1-0.25*0.25 - 0.0625*(-0.243567) - 0.0625*(-0.2421875))/1) = -0.255946
y1 = 1 + (-0.25 + 2*(-0.2421875) + 2*(-0.243567) + (-0.255946))/6 = 0.78991
Thus, using fourth-order Runge-Kutta method with h=0.25, we have obtained the approximate solution of the given initial value problem at x=1.
Using the Taylor method of order 4, the solution to the initial value problem is given by the formula,
\(y(x) = y0 + f0(x-x0) + f0'(x-x0)(x-x0)/2! + f0''(x-x0)^2/3! + f0'''(x-x0)^3/4! + ........\)
where
y(x) = solution to the initial value problem
y0 = initial value of y
f0 = f(x0,y0) = x0 - y0
f0' = ∂f/∂y = -1
\(f0'' = ∂^2f/∂y^2 = 0\\f0''' = ∂^3f/∂y^3 = 0\)
Therefore, substituting these values in the above formula, we get:
\(y(x) = 1 + (x-0) - (x-0)^2/2! + (x-0)^3/3! - (x-0)^4/4!\)
Simplifying, we get:
\(y(x) = x - x^2/2 + x^3/6 - x^4/24\)
Thus, using the Taylor method of order 4, the solution to the given initial value problem is\(y(x) = x - x^2/2 + x^3/6 - x^4/24\).
Learn more about Runge-kutta here:
https://brainly.com/question/31854918
#SPJ11
In predicate calculus, arguments to predicates and functions can only be terms - that is, combinations of __. Select one: a. predicates and connectives b. constants and predicates c. variables, constants, and functions d. predicates, quantifiers, and connectives
Answers
Answer:
c. variables, constants, and functions
Step-by-step explanation:
A predicate is the property that some object posses. Predicate calculus is a kind of logic that combines the categorical logic with propositional logic. The formal syntax of a predicate calculus contains 3 Terms which consist of:
1. Constants and Variables
2. Connectives
3. Quantifiers
But in arguments to predicates and functions, the terms can only be combination of variables, constants, and functions.
factor the following expression using imaginary numbers : 100x^2+1
Answers
Hence, the factors of \((10x+1)^2=100x^2+1+20x\).
What are the factorization?
Factorisation or factoring is defined as the breaking or decomposition of an entity into a product of another entity, or factors, which when multiplied together give the original number.
Here given expression is
\(100x^2+1\)
\((10x)^2+(1)^2\)
\((10x+1)^2\)
As we know that,
\((a+b)^2=a^2+b^2+2ab\)
Here
\(a=10x\\b=1\)
So,
\((10x+1)^2=(10x)^2+(1)^2+2(10x(1))\\\\(10x+1)^2=(10x)^2+(1)^2+20x\\\\(10x+1)^2=100x^2+1+20x\)
Hence, the factors of \((10x+1)^2=100x^2+1+20x\).
To know more about the factorization
https://brainly.com/question/29216619
#SPJ1
The factors of the expression 100x² + 1 are (10x+i) (10x-i).
What is a quadratic function?A polynomial function with one or more variables, where the largest exponent of the variable is two, is referred to as a quadratic function. In other terms, a "polynomial function of degree 2" is a quadratic function.
The given expression is 100x² + 1.
The given expression is a quadratic function.
The standard form of quadratic function:
ax²+bx +c, where a is not equals to zero.
Comparing with the standard form we get,
a = 100, b = 0 and c = 1
Simplifying,
100x² + 1
= 100x² - (-1)
= (10x)² - (-1)
= (10x)² - (i)² ,{i² = -1}
= (10x+i) (10x-i)
Therefore, (10x+i) (10x-i) are the factors.
To learn more about the quadratic function;
https://brainly.com/question/11485644
#SPJ1
Write the statements of the following algebraic expressions!
A- a+1
B- q-9
C- 3y+7
D- x/3+9
E- 3x+10
Answers
Answer:
See below ↓↓↓↓↓
Step-by-step explanation:
A - the sum of a number 'a' and 1B - the difference between a number 'q' and 9C - 7 plus the product of a number 'y' and 3D - 9 plus the quotient of a number 'x' and 3E - 10 plus the product of a number 'x' and 3= 1 more than a number (a)
B- q-9= q less than 9
C- 3y+7= 3 times y added to 7
D- x/3+9= a number (x) divided by 3 more than 9
E- 3x+10= 3 times x added to 10
Kiran paid $54.00 for 3 tickets to go to a corn maze. At the same rate, what is the cost of 5 tickets to the maze? *
Answers
Answer:90
Step-by-step explanation:
Answer: $90
Step-by-step explanation:
You can set up a proportion.
$54 = 3 tickets
x = 5 tickets
To find x, multiply 54 and 5.
54 × 5 = 270
Then divide 270 by 3.
270 ÷ 3 = $90
Since we figured out x = $90, this means that it costs $90 for 5 tickets.
hope this helps!!
Choices are...
A)1120
B)2275
C)3500
D)2345
It's Side Splitter Theorem

Answers
Answer:
B
Step-by-step explanation:
The sections of the parallel roads split by the transversals are in proportion, that is
\(\frac{350}{300}\) = \(\frac{first}{1650}\) ( cross- multiply )
300 first = 577500 ( divide both sides by 300 )
first = 1925 ft
Thus
Elm st → Maple st = 1925 + 350 = 2275 ft → B
which shows the price of a $35 video game after a mark up 27%
Answers
Answer:
Step-by-step explanation:
35*27%=9.45 mark up
35+9.45= 44.45 total cost
Answer:
The answer is $44.45
Step-by-step explanation:
You change the percent into a decimal so it would be .27 then multiply the .27 to the $35 and you will get $9.45. Then you add the $9.45 to the $35 and you will get the answer.