given that nafeli answered correctly the first question, what is the probability that she knew the answer to that question?
Answers
The posterior PMF of the number of questions Nefeli knew the answer to, given that she answered 6 out of 10 questions correctly, is: \(P(K=k|6 correct answers) = (k choose 6) / (3^k)\), for k = 0 to 6, and 0 otherwise.
To determine the posterior probability mass function (PMF) of the number of questions Nefeli knew the answer to, given that she answered 6 out of 10 questions correctly, we can use Bayesian inference and apply the concept of conditional probability.
Let's define the following variables:
- K: The number of questions Nefeli knew the answer to.
- G: The number of questions Nefeli guessed the answer to.
We want to find the PMF of K, given that she answered 6 questions correctly. This can be expressed as P(K | 6 correct answers).
By Bayes' theorem, we have:
P(K | 6 correct answers) = P(6 correct answers | K) * P(K) / P(6 correct answers)
Let's break down each term:
1. P(6 correct answers | K):
If Nefeli knew the answer to K questions, the probability of getting 6 correct answers out of K is given by the binomial distribution. The probability of answering a question correctly is 1 since she knows the answer, so the probability of getting 6 correct answers out of K is \((K choose 6) * (1^6) * (0^{(K-6)})\), where (K choose 6) is the binomial coefficient.
\(P(6 correct answers | K) = (K choose 6) / 3^K\)
2. P(K):
The prior probability of Nefeli knowing the answer to K questions. Since each question is independent, we can assume a uniform prior distribution, where P(K) is constant for all possible values of K.
P(K) = 1 / (total number of possible values of K)
3. P(6 correct answers):
The marginal probability of getting 6 correct answers, regardless of the number of questions Nefeli knew the answer to. This can be calculated by summing the joint probabilities over all possible values of K and G.
P(6 correct answers) = Σ[over all possible values of K and G] P(6 correct answers | K, G) * P(K) * P(G)
To compute the marginal probability P(6 correct answers), we need to consider all possible combinations of K and G that satisfy K + G = 10 (since there are 10 questions in total). We will iterate over all possible values of K and G and calculate the corresponding joint probability P(6 correct answers | K, G) * P(K) * P(G). Finally, we normalize these probabilities to obtain the posterior PMF.
Here's a Python code snippet that computes the posterior PMF:
```python
import math
def binomial_coefficient(n, k):
return math.factorial(n) // (math.factorial(k) * math.factorial(n - k))
def posterior_pmf_of_k(k, correct_answers):
return (binomial_coefficient(k, correct_answers) * (1/3) ** k)
def compute_posterior_pmf(correct_answers):
pmf = {}
total_p = 0
for k in range(correct_answers + 1):
g = correct_answers - k
p = posterior_pmf_of_k(k, correct_answers)
pmf[k] = p
total_p += p
for k in pmf:
pmf[k] /= total_p
return pmf
correct_answers = 6
posterior_pmf = compute_posterior_pmf(correct_answers)
print(posterior_pmf)
The `posterior_pmf` dictionary will contain the posterior probabilities for each possible value of K. The output will show the posterior PMF for the number of questions Nefeli knew the answer to, given that she answered 6 out of 10 questions correctly.
Learn more about Bayes' theorem here: https://brainly.com/question/33143420
#SPJ11
The complete question is:
Nefeli. a student in a probability class, takes a multiple-choice test with 10 questions and 3 choices per question. For each question. there are two equally likely possibilities, independent of other questions: either she knows the answer, in which case she answers the question correctly. or else she guesses the answer with probability of success 1/3. Given that Nefeli answered correctly 6 out of the 10 questions, what is the posterior PMF of the number of questions of which she knew the answer?
Related Questions
help -------------------------

Answers
Answer:
(A) -3 ≤ x ≤ 1
Step-by-step explanation:
The given function is presented as follows;
h(x) = x² - 1
From the given function, the coefficient of the quadratic term is positive, and therefore, the function is U shaped and has a minimum value, with the slope on the interval to the left of h having a negative rate of change;
The minimum value of h(x) is found as follows;
At the minimum of h(x), h'(x) = d(h(x)/dx = d(x² - 1)/dx = 2·x = 0
∴ x = 0/2 = 0 at the minimum
Therefore, the function is symmetrical about the point where x = 0
The average rate of change over an interval is given by the change in 'y' and x-values over the end-point in the interval, which is the slope of a straight line drawn between the points
The average rate of change will be negative where the y-value of the left boundary of the interval is higher than the y-value of the right boundary of the interval, such that the line formed by joining the endpoints of the interval slope downwards from left to right
The distance from the x-value of left boundary of the interval that would have a negative slope from x = 0 will be more than the distance of the x-value of the right boundary of the interval
Therefore, the interval over which h has a negative rate of change is -3 ≤ x ≤ 1


Find the cube root of -8.
Answers
Answer:
The cube root of -8 is -2
Step-by-step explanation:
Factor the numbers 8=2^3
-∛2³
Apply radical rule;
∛2³=2
=-2
HOPE THIS HELPED!!!
Phillip and his two friends need to raise at least $2,400 for their study abroad trip to Europe. So far, they have raised $600. Write an inequality to represent x, the amount of money they need to raise after the first week. Explain your answer.
Answers
Answer:
x + 600 ≥ 2400
Step-by-step explanation:
Given:
Amount needed = $2,400
Amount they had = $600
Find:
Amount they need
Computation:
Assume;
Amount they need = x
x + 600 ≥ 2400
how many days are there from 14 February to 3 April if it was a leap year
Answers
Answer:
49 days
Step-by-step explanation:
answer forty nine days
The triangle is shown below
what is the value of x
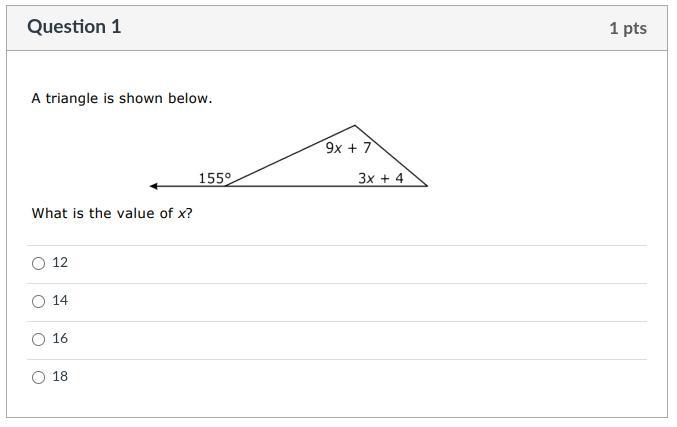
Answers
Answer: x=12
Step-by-step explanation:
88 + 32 = 8(___ + 4)
Answers
114 = 8(x + 4)
114 = 8x +32
-32. -32
82 = 8x
—- —-
8. 8
10.25 is the answer
a carpenter and his assistant can do a piece of work in 3 days. if the carpenter himself could do the work alone in 5 days, how long would the assistant take to do the work alone?
Answers
The number of days spent or taken by assistant with work efficiency of 2 units per day to do the work alone is equals to the 7.5 days.
We have provide that there is a carpenter and his assistant can do a piece of work.
Number of days taken by both carpenter and his assistant to do a piece of work = 3 days.
Number of days taken by carpenter and to do the same piece of work alone = 5 days.
We have to determine number of taken by assistant and to do the same piece of work alone.
Let the required number of days that the assistant take to do the work alone be 'x days'. As we know, total available work units = LCM (3,5) = 15 units
Ability or efficiency of a person or man is calculated by dividing the total work units to the number of working days spent to do the work.
Now, Ability or efficiency of both carpenter and his assistant work together = 15/5
= 3 units/day
Similarly, Ability or efficiency of carpenter = 15/3
= 5 units/day
So, Ability or efficiency of assistant= 5 - 3 = 2 -(1)
Using efficiency formula, efficiency of assistant
= 15/x --(2)
from (1) and(2), 15/x = 2
=> 2x = 15
=> x = 7.5
Hence, required number of days are 7.5 days.
For more information about work-efficiency formula, refer:
#SPJ4
Graph Z=3cos315+3isin315 explain where you would find this equation on a complex plane
Answers
Answer:
cos 315° = 45° reference angle in the 4th quadrant = √2 /2
And sin 315° is the negative of this
So
z = (3) cos 315° + ( 3i ) sin 315° =
[ (3/2)√2 , - (3/2) √2 i ]
If you want to maximize your probability of winning, what threshold should you set for your strategy in a gameof 10 flips
Answers
It's important to approach any strategy with caution and understand its limitations.
If one wants to maximize their probability of winning in a game of 10 flips, they should set the threshold at 6.
This is because when playing a game of 10 coin flips, there are 2^10 or 1024 possible outcomes, with 512 of them resulting in a win, a loss, or a tie.
Therefore, setting the threshold at 6 ensures that they win at least 6 out of the 10 coin flips, resulting in a higher probability of winning.
However, it's worth noting that this strategy is not foolproof as it does not take into account the sequence of the coin flips.
For example, if the first 5 coin flips are tails and the last 5 are heads, setting the threshold at 6 would result in a loss.
Therefore, it's important to approach any strategy with caution and understand its limitations.
learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
The function p(s)=−10s2+110s−180 represents a company's profit p made on selling a product for s dollars per unit. Calculate and interpret p(6). (1 point)
1. If the company wants to make a profit of $6, they need to sell units for either $2 or $9.
2. The company's profit from selling their product for $6 per unit is $120.
3. If the company wants to make a profit of $6, they need to sell either 2 or 9 units.
4. The company's profit from selling 6 units is $120.
Answers
Answer:
2. The company's profit from selling their product for $6 per unit is $120.
Step-by-step explanation:
If we graph this function on a 2-axis plane such that the horizontal axis (x) represents \(s\), or the product's price per unit and the vertical axis (y) represents \(p(s)\), or the profit made by selling the product at \(s\) dollars, we'll find that the \(p\)-coordinate of the point where \(s=6\) is 120. Hence, $120 profit will be made if the product is sold at $6 per unit.
See the attached image for a graph.

Ayden is a salesperson who sells computers at an electronics store. He makes a base pay amount of $90 per day regardless of sales and he earns a commission of 1% of the dollar amount of all sales that he makes. Write an equation for the function P(x),P(x), representing Ayden's total pay on a day on which he sells xx dollars worth of computers
Answers
The function P(x) representing Ayden's total pay on a day on which he sell x dollar worth of computers is P(x) = 0.01x + 90
The base pay amount of Ayden per regardless of sales = $90
The commission of Ayden = 1% of the dollar amount of sales
Consider the total sales amount in a day as x
The function is the mathematical expression that shows the relationship between one variable and another variable. If one variable is dependent variable then the other variable will be independent variable.
Then the function will be
P(x) = 1% of x + 90
= 0.01x + 90
Therefore, the equation for the function P(x) = 0.01x + 90
Learn more about function here
brainly.com/question/10454465
#SPJ4
4. Consider the function f(x)=x^2-4
Part A: Write a function that shifts f(x) left 5 units.
Part B: Write a function that shifts f(x) right 8units.
Part C: Write a function that horizontally stretches f(x) by 1/4 units.
Part D: Write a function that horizontally compresses f(x) by 6 units.
HELP!!!! PLSSSS
Answers
Using translation concepts, it is found that the modified functions are:
A. \(g(x) = x^2 + 10x + 21\)
B. \(g(x) = x^2 - 16x + 60\)
C. \(g(x) = 16x^2 - 4\)
D. \(g(x) = \frac{x^2 - 4}{6}\)
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.In this problem, the function is given by:
\(f(x) = x^2 - 4\)
Item a:
For a shift left of 5 units, we have \(f(x + 5)\), hence:
\(g(x) = f(x + 5) = (x + 5)^2 - 4 = x^2 + 10x + 25 - 4 = x^2 + 10x + 21\)
Item b:
For a shift right of 8 units, we have \(f(x - 8)\), hence:
\(g(x) = f(x - 8) = (x - 8)^2 - 4 = x^2 - 16x + 64 - 4 = x^2 - 16x + 60\)
Item c:
For a horizontal stretch by a factor of 1/4, we find \(f(4x)\), hence:
\(g(x) = f(4x) = (4x)^2 - 4 = 16x^2 - 4\)
Item d:
For a vertical compression by a factor of 1/6, we find \(\frac{1}{6}f(x)\), hence:
\(g(x) = \frac{1}{6}f(x) = \frac{x^2 - 4}{6}\)
You can learn more about translation concepts at https://brainly.com/question/4521517
6 - 3/4x + 1/3 = 1/2x + 5
help
Answers
Answer:
x=15/16
Step-by-step explanation:
Let's solve your equation step-by-step.
6−34x+13=12x+5
6+−34x+13=12x+5
Multiply all terms by x and cancel:
6x+−34+1x3=12+5x
193x+−34=5x+12(Simplify both sides of the equation)
193x+−34−5x=5x+12−5x(Subtract 5x from both sides)
43x+−34=12
43x+−34+34=12+34(Add 3/4 to both sides)
43x=54
(34)*(43x)=(34)*(54)(Multiply both sides by 3/4)
x=1516
Check answers. (Plug them in to make sure they work.)
x=1516(Works in original equation)
8 out of 32 is same as??
Please tell me solution with all steps
Answers
Answer:
4
Step-by-step explanation:
32/8
= 4
Pls mark as branlist
Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is placed. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.
Place the indicated product in the proper location on the grid.
(a + b )(a - 2b )
Answers
The product of the expression (a + b) and (a - 2b) will be a² - ab - 2b².
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
The expressions are given below.
(a + b) and (a - 2b)
Then the product of the expression is given as,
⇒ (a + b)(a - 2b)
⇒ a² - 2ab + ab - 2b²
⇒ a² - ab - 2b²
The product of the expression (a + b) and (a - 2b) will be a² - ab - 2b².
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
Find h as indicated in the figure. Round to the nearest foot.
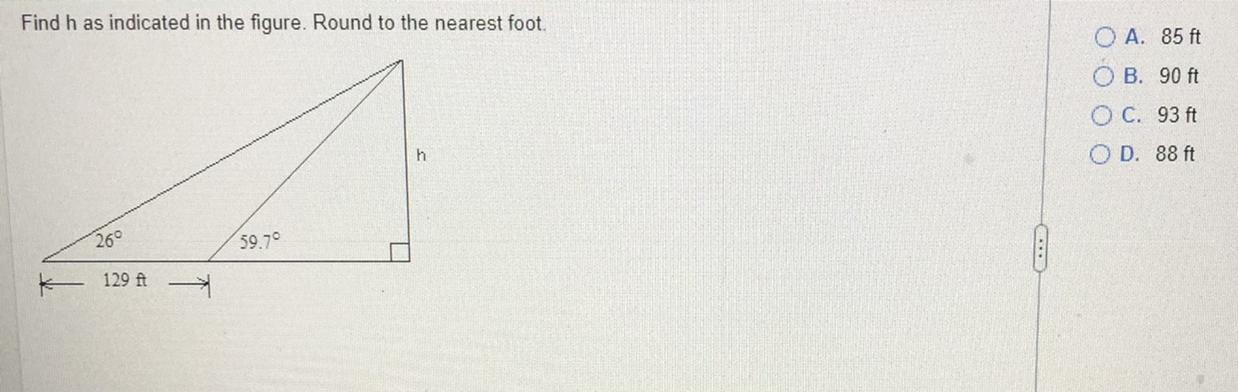
Answers
By using trigonometric functions and law of sines, the length h indicated in the figure is approximately 87.997 feet.
What is the value of a length of a triangle within a geometric system?
In this system we find a picture of a geometric system formed by the two triangles, one of which with a right angle. We need to use trigonometric functions, law of sines and law of cosine to determine the missing length. First, use the law of sines:
(129 ft) / sin 33.7° = r / sin 26°
r = 129 ft × sin 26° / sin 33.7°
r ≈ 101.920 ft
Lastly, we find the value of the length h by trigonometric functions:
h = r · sin 59.7°
h = (101.920 ft) · sin 59.7°
h ≈ 87.997 ft
The length h indicated in the figure is approximately 87.997 feet.
To learn more on trigonometric functions: https://brainly.com/question/14746686
#SPJ1
the only calculated fields you can create in access are those involving addition and subtraction. True or false?
Answers
Answer:
false
Step-by-step explanation:
False.
Access supports a wide range of built-in functions and operators that can be used to create calculated fields. These functions and operators include mathematical functions (such as multiplication, division, exponentiation), string functions (such as concatenation, trimming, and formatting), date and time functions, aggregate functions (such as sum, average, count), and more.
In addition, Access also allows you to create user-defined functions using VBA (Visual Basic for Applications), which can be used to perform custom calculations on your data.
Therefore, the statement "the only calculated fields you can create in Access are those involving addition and subtraction" is false.
learn more about 'function'
#SPJ11
Find f[g(x)] and g[f(x)] for the given functions. 3 f(x) = -x³ +3, g(x) = 4x+7 (Simplify your answer. Do not factor.) (Simplify your answer. Do not factor.) f[g(x)] = g[f(x)] =
Answers
The value of f[g(x)] is - 64x³ - 336x² - 588x - 340 and the value of g[f(x)] is -4x³ + 19
The functions are as follows; f(x) = -x³ +3 and g(x) = 4x+7
The value of f[g(x)] is obtained by replacing every x in f(x) with the value of g(x) as given below
f[g(x)] = f(4x + 7) = - (4x + 7)³ + 3
When we expand (4x + 7)³, it gives us 64x³ + 336x² + 588x + 343
Then
f[g(x)] = - 64x³ - 336x² - 588x - 340
Similarly, g[f(x)] is obtained by replacing every x in g(x) with the value of f(x) as shown below;
g[f(x)] = g(-x³ + 3) = 4(-x³ + 3) + 7g
[f(x)] = -4x³ + 19
Therefore,
f[g(x)] = - 64x³ - 336x² - 588x - 340
g[f(x)] = -4x³ + 19
Learn more about the function at
https://brainly.com/question/32520165
#SPJ11
Need help with this geometry problem hard for me smart people only 100% pls fast due now

Answers
Answer:
x = 30°
Step-by-step explanation:
We know that the sum of all of the interior angles of a triangle is 180°, therefore, we can write the following equation:
x + 2x + 3x = 180
6x = 180
x = 30°
solve for ΔABC
20 POINTS

Answers
Answer:
a2=b2+c2-2bc cos a
Step-by-step explanation:
Multiply the following polynomials

Answers
The product of (t + 5) and (t² + 3t + 10) is t³ + 8t² + 25t + 50.
What is polynomial?
A polynomial is a mathematical expression that consists of variables and coefficients, which are combined using arithmetic operations such as addition, subtraction, multiplication, and non-negative integer exponents.
We can use the distributive property to multiply these two polynomials:
(t + 5)(t² + 3t + 10) = t(t² + 3t + 10) + 5(t² + 3t + 10)
Now we need to simplify each of these terms:
t(t² + 3t + 10) = t³ + 3t² + 10t
5(t² + 3t + 10) = 5t² + 15t + 50
Putting them together, we have:
(t + 5)(t² + 3t + 10) = t³ + 3t² + 10t + 5t² + 15t + 50
Now we can combine like terms:
t³ + 8t² + 25t + 50
Therefore, the product of (t + 5) and (t² + 3t + 10) is t³ + 8t² + 25t + 50.
To learn more about polynomial from the given link:
https://brainly.com/question/29073508
#SPJ1
This time he did look me in the eyes.(How many verbs does this sentence contain?)
Answers
if p = 2^k + 1 is prime, show that every quadratic nonresidue of p is a primitive root of p.
Answers
Every quadratic nonresidue of p is a primitive root of p, when p = 2^k + 1 is primeIf p = 2^k + 1 is a prime number, we want to show that every quadratic nonresidue of p is a primitive root of p.
In other words, we aim to prove that if an element x is a quadratic nonresidue modulo p, then it is also a primitive root of p.
Let's assume p = 2^k + 1 is a prime number. To prove that every quadratic nonresidue of p is a primitive root of p, we can use the properties of quadratic residues and quadratic nonresidues.
A quadratic residue modulo p is an element y such that y^((p-1)/2) ≡ 1 (mod p), while a quadratic nonresidue is an element x such that x^((p-1)/2) ≡ -1 (mod p).
Now, let's consider an element x that is a quadratic nonresidue modulo p. We want to show that x is a primitive root of p.
Since x is a quadratic nonresidue, we know that x^((p-1)/2) ≡ -1 (mod p). By Euler's criterion, this implies that x^((p-1)/2) ≡ -1^((p-1)/2) ≡ -1^2 ≡ 1 (mod p).
Since x^((p-1)/2) ≡ 1 (mod p), we can conclude that the order of x modulo p is at least (p-1)/2. However, since p = 2^k + 1 is a prime, the order of x modulo p must be equal to (p-1)/2.
By definition, a primitive root of p has an order of (p-1). Since the order of x modulo p is (p-1)/2, it follows that x is a primitive root of p.
Learn more about Euler's criterion here:
brainly.com/question/12977984
#SPJ11
Alan mixes cups of milk with a can of condensed soup. he makes a total of cups of soup. how many cups of condensed soup were in the can?
Answers
1 (7/24) cups of condensed soup were in the can.
Given,
There is a can of condensed soup .
The amount of milk Alen mixes with the condensed soup = 1 1/3
Subtract amount of milk from total cups of soup:
2 ( 5/8 ) – 1 ( 1/3 )
Make the fraction in same form to make the subtraction easy.
2 ( 5/24 ) – 1 ( 8/24 )
Now solve
2 (15/24 ) – 1 ( 8/24 )= 1 ( 7/24 )
Here, there is 1 ( 7/24 ) cups of condensed soup in the can.
Learn more about fraction calculation here: https://brainly.com/question/644022
#SPJ4
The question is incomplete. And the corrected question is given below.
Alan mixes 1 1/3 cups of milk with a can of condensed soup. he makes a total of 2 5/8 cups of soup. how many cups of condensed soup were in the can?
Look at the two patterns below: Pattern A: Starts at 5 and follows the rule "add 6" Pattern B: Starts at 5 and follows the rule "add 3" Select the statement that is true. (4 points) a The terms in Pattern A are 2 times the corresponding terms in Pattern B. B The terms in Pattern B are one third the corresponding terms in Pattern A. C The first five terms in Pattern A are 5, 11, 17, 23, and 29. D The first five terms in Pattern B are 0, 5, 8, 11, 14.
Answers
Answer:
The first five terms in Pattern A are 5, 11, 17, 23, and 29
Step-by-step explanation:
Pattern A:
5 + 6a
Pattern B:
5 + 3a
Take a = 1 and compare ;
Pattern A:
5 + 6(1) = 11
Pattern B:
5 + 3(1) = 8
A ≠ 2B
B ≠ 1/3A
First 5 terms in pattern A :
Pattern A:
5
5 + 6(1) = 11
5 + 6(2)= 17
5 + 6(3) = 23
5 + 6(4) = 29
5 + 6(5) = 35
Pattern B cannot have a term 0 as it starts from 5
A company is considering spending $159,000 at Time 0 to test a new product. Depending on the test results, the company may decide to spend $1,161,000 at Time 1 to start production of the product. If the product is introduced and it is successful, it will produce aftertax cash flows of $543,000 a year for Years 2 through 6. The probability of successful test and investment is 70 percent. What is the net present value at Time 0 given a 11 percent discount rate? $317,221.10 $336,291.68 $355,362.26 $374,432.84 $393,503.42
Answers
To calculate the net present value (NPV) at Time 0, we need to discount the cash flows from Years 2 through 6 to their present value, and then compare it to the initial investment at Time 0.
Let's break down the calculation step by step:
Calculate the present value of cash flows from Years 2 to 6:
The cash flow for each year is $543,000.
Since the cash flows are received annually, we need to discount them by the appropriate discount rate for each year.
The discount rate is 11 percent.
Using the formula for the present value of a cash flow, we can calculate the present value for each year:
PV = CF / (1 + r)^n
Where PV is the present value, CF is the cash flow, r is the discount rate, and n is the year.
Calculating the present value for each year:
PV2 = $543,000 / (1 + 0.11)^2
PV3 = $543,000 / (1 + 0.11)^3
PV4 = $543,000 / (1 + 0.11)^4
PV5 = $543,000 / (1 + 0.11)^5
PV6 = $543,000 / (1 + 0.11)^6
Calculate the probability-weighted present value of cash flows from Years 2 to 6:
The probability of a successful test and investment is 70 percent.
Multiply each present value by the probability to get the probability-weighted present value.
PWPV2 = 0.7 * PV2
PWPV3 = 0.7 * PV3
PWPV4 = 0.7 * PV4
PWPV5 = 0.7 * PV5
PWPV6 = 0.7 * PV6
Calculate the total present value of cash flows:
Add up the probability-weighted present values.
Total PV = PWPV2 + PWPV3 + PWPV4 + PWPV5 + PWPV6
Calculate the net present value at Time 0:
Subtract the initial investment at Time 0 from the total present value.
NPV = Total PV - $159,000
Now, let's perform the calculations:
PV2 = $543,000 / (1 + 0.11)^2 = $543,000 / 1.2321 ≈ $441,648.60
PV3 = $543,000 / (1 + 0.11)^3 = $543,000 / 1.3676 ≈ $397,431.88
PV4 = $543,000 / (1 + 0.11)^4 = $543,000 / 1.5162 ≈ $358,262.97
PV5 = $543,000 / (1 + 0.11)^5 = $543,000 / 1.6782 ≈ $323,335.62
PV6 = $543,000 / (1 + 0.11)^6 = $543,000 / 1.8550 ≈ $292,290.66
PWPV2 = 0.7 * $441,648.60 ≈ $309,154.02
PWPV3 = 0.7 * $397,431.88 ≈ $278,202.32
PWPV4 = 0.7 * $358,262.97 ≈ $250,784.08
PWPV5 = 0.7 * $323
Learn more about net present value at https://brainly.com/question/32628379
#SPJ11
The net present value at Time 0, given an 11 percent discount rate, is $374,432.84.
What is the net present value at Time 0?The net present value (NPV) is a financial metric that measures the profitability of an investment by calculating the present value of expected cash flows. It takes into account the time value of money, which means that future cash flows are discounted to their present value.
Step 1: To calculate the NPV, we need to discount the expected cash flows to Time 0 using the given discount rate of 11 percent. The cash flows include the initial testing cost, production cost, and aftertax cash flows for Years 2 through 6.
Step 2: By discounting the cash flows, we find that the NPV at Time 0 is $374,432.84.
Step 3: The NPV represents the expected profitability of the investment. A positive NPV indicates that the investment is expected to generate more value than the initial cost. In this case, the positive NPV of $374,432.84 suggests that the investment is likely to be profitable, considering the expected cash flows and the discount rate.
Learn more about net present value
brainly.com/question/31984281
#SPJ11
suppose the real risk-free rate is 2.50% and the future rate of inflation is expected to be constant at 2.80%. what rate of return would you expect on a 5-year treasury security, assuming the pure expectations theory is valid? disregard cross-product terms, i.e., if averaging is required, use the arithmetic average.
Answers
5.30 % rate of return would you expect on a 5-year treasury security, assuming the pure expectations theory is valid.
Real and nominal interest rates: what are they?To reflect the true cost and purchasing power of money that is borrowed or invested, an interest rate is called a real interest rate that has been adjusted for inflation. The nominal interest rate depicts the cost of money and reflects the state of the market. A good's nominal value is its price in terms of money. Its value in relation to another good, service, or collection of goods is what determines its true worth. Given that it is the current interest rate in the economy, it is frequently referred to as the market interest rate (usually charged by banks and other institutions). Depending on the bank or the type of loans or deposits, this nominal interest rate may be 8%, 10%, or 12%.
Nominal interest rate = Real interest rate + Inflation rate
= 2.5% + 2.8%
= 5.30%
Learn more about the Nominal interest rate here: https://brainly.com/question/25877453
#SPJ1
Is there a right answer to this question

Answers
Answer:
answer C
Step-by-step explanation:
I had the same test question
Consider the following rounds of Tug-O-War. - Round 1: Four grad students (all of equal strength) go against five professors (all of equal strength). - The match is a tie. Neither side can move the other. - Round 2: A bull goes against two professors and one grad student. - The match is a tie. Neither side can move the other. - Round 3 : A bull and three professors are on one side. Three grad students are on the other. - Who wins Round 3? Post your solution and explain your reasoning. Consider how children could use arithmetic and algebra to work these problems.
Answers
In Round 3, the side with the bull and three professors wins against the three grad students due to their combined strength advantage. So the correct answer is Round 3.
In Round 3, the side with the bull and three professors wins against the three grad students. This outcome is based on the assumption that the combined strength of the bull and the professors is greater than the combined strength of the grad students.
Arithmetic and algebra can be used to analyze this situation. Let's assign a numerical value to the strength of each participant. Suppose the strength of each grad student and professor is 1, and the strength of the bull is 5.
On one side, the total strength is 3 (grad students) + 5 (bull) = 8.
On the other side, the total strength is 3 (professors) = 3.
Since 8 is greater than 3, the side with the bull and three professors has a higher total strength and wins Round 3.
Learn more about Arithmetic click here :brainly.com/question/6561461
#SPJ11
Let m = x^2 - 5
Which equation is equivalent to (x^2-5)^2 - 3x^2 + 15= -2 in terms of m ?
A m^2+3m+2=0
B m^2-3m+17=0
C m^2-3m+2=0
D m^2+3m+17=0
Thanks!
Answers
The equivalent equation to the (x² - 5)² - 3x² + 15 = -2 in form of 'm' is given by option c. m² -3m + 2 = 0.
The equation is equal to,
(x² - 5)² - 3x² + 15 = -2
let the value of m be equals to x² - 5.
Simplify the equation we have,
⇒ ( x² - 5 )² - 3x² + 15 = -2
Take '3' common factor from the 3x² + 15 so that it get convert into x² - 5 we get,
⇒ ( x² - 5 )² - 3 (x² - 5 ) = -2
Now replace x² - 5 by m to get the equivalent equation,
⇒ ( m )² - 3 (m ) = -2
⇒ m² -3m + 2 = 0
Therefore, the equivalent equation to the given equation is written as option c. m² -3m + 2 = 0.
Learn more about equivalent here
brainly.com/question/16415525
#SPJ1