Helppp pleaseee i would appreciate it
A car was valued at $28,000 in the year 1990. The value depreciated to $10,000 by the year 2000.
A) What was the annual rate of change between 1990 and 2000?
r= ---------- Round the rate of decrease to 4 decimal places.
B) What is the correct answer to part A written in percentage form?
r= ------------%
C) Assume that the car value continues to drop by the same percentage. What will the value be in the year 2005 ?
value = $ ------------- Round to the nearest 50 dollars.
Answers
The term "annual rate" can be used to describe any rate that is calculated over a year. For instance, if a business says that its revenue growth rate is 10% annually, it means that during the previous year or years, its revenue has climbed by 10% on average annually.
What is the annual rate?A) To find the annual rate of change, we can use the formula:
\(r = (V2/V1)^(1/n) - 1\)
where V1 is the initial value, V2 is the final value, and n is the number of years between the two values.
Substituting the values given in the problem, we get:
\(r = (10000/28000)^(1/10) - 1\)
\(r ≈ -0.0935\)
Therefore, the annual rate of change between \(1990\) and \(2000\)is approximately -0.0935.
B) To convert the rate to a percentage, we can multiply by 100 and add a percent sign:
\(r ≈ -9.35%\)
Therefore, the correct answer to part A written in percentage form is approximately \(-9.35%.\)
C) If we assume that the car value continues to drop by the same percentage, we can use the formula:
\(V = V0*(1+r)^n\)
where V0 is the initial value, r is the annual rate of change (as a decimal), and n is the number of years.
Substituting the values given in the problem, we get:
\(V = 10000*(1-0.0935)^5\)
\(V ≈ $5,685\)
Therefore, the value of the car in the year 2005 would be approximately \($5,700\) (rounded to the nearest 50 dollars).
Learn more about rate here:
https://brainly.com/question/17613825
#SPJ1
Related Questions
Use the vertex and intercepts to sketch the graph of the quadratic function. Give the equation for the parabola's axis of symmetry. Use the graph to determine the function's domain and range.
f(x) =x^2 +12x+6
What is the vertex?
What are the x-intercepts?
What is the y-intercept?
what is the axis of symmetry?
Identify the function's domain
Identify the function's range.
Answers
The Vertex is : (-6, -30)
The X-intercepts are : Approximately (-10.89, 0) and (-1.11, 0)
The Y-intercept is : (0, 6)
The Axis of symmetry is : x = -6
The functions Domain: is All real numbers
The Range is : All real numbers greater than or equal to -30.
To sketch the graph of the quadratic function \(f(x) = x^2 + 12x + 6,\) we can start by identifying the vertex, x-intercepts, y-intercept, axis of symmetry, domain, and range.
To find the vertex, we can use the formula x = -b/2a, where a, b, and c are the coefficients of the quadratic equation in standard form\((ax^2 + bx + c).\)
In this case, a = 1, b = 12, and c = 6.
Applying the formula, we get x = -12/(2 \(\times\) 1) = -6.
To find the y-coordinate of the vertex, we substitute this x-value into the equation:\(f(-6) = (-6)^2 + 12(-6) + 6 = 36 - 72 + 6 = -30.\)
So, the vertex is (-6, -30).
To determine the x-intercepts, we set f(x) = 0 and solve for x. In this case, we need to solve the quadratic equation \(x^2 + 12x + 6 = 0.\)
Using factoring, completing the square, or the quadratic formula, we find that the solutions are not rational.
Let's approximate them using decimal values: x ≈ -10.89 and x ≈ -1.11. Therefore, the x-intercepts are approximately (-10.89, 0) and (-1.11, 0).
The y-intercept is obtained by substituting x = 0 into the equation: \(f(0) = 0^2 + 12(0) + 6 = 6.\)
Thus, the y-intercept is (0, 6).
The axis of symmetry is the vertical line that passes through the vertex. In this case, it is the line x = -6.
The domain of the function is all real numbers since there are no restrictions on the possible input values of x.
To determine the range, we can observe that the coefficient of the \(x^2\) term is positive (1), indicating that the parabola opens upward.
Therefore, the minimum point of the parabola occurs at the vertex, (-6, -30).
As a result, the range of the function is all real numbers greater than or equal to -30.
For similar question on Vertex.
https://brainly.com/question/25651698
#SPJ8

HELPPP ASPA 60 POINT!!!!!Show to draw a line segment that measures 92 millimeters. i need it to be in words not a photo please
Answers
A line segment that measures 92 millimeters in length can be drawn using scale.
Given that,
A line segment has to be drawn which has a measure of length 92 millimeters.
We know that,
10 millimeters = 1 centimeter
1 millimeter = 1/10 centimeters
92 millimeters = 92/10 = 9.2 centimeters
So it is enough to draw a line segment of length 9.2 centimeters.
In the scale, between a centimeter, there are 9 small lines which indicates the millimeters.
In between 9 and 10, there are 9 lines which indicates, 9.1, 9.2, 9.3, ....., 9.9 and after that is 10 cm.
So draw a line segment starting from 0 to 9.2.
Hence the line segment is drawn with scale.
Learn more about Line Segments here :
https://brainly.com/question/9477630
#SPJ1
Find the open intervals on which the function f(x)= x+10sqrt(9-x) is increasing or decreasing.

Answers
The function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
To determine the intervals on which the function is increasing or decreasing, we need to find the derivative of the function and analyze its sign.
Let's find the derivative of the function f(x) = x + 10√(9 - x) with respect to x.
f'(x) = 1 + 10 * (1/2) * (9 - x)^(-1/2) * (-1)
= 1 - 5√(9 - x) / √(9 - x)
= 1 - 5 / √(9 - x).
To analyze the sign of the derivative, we need to find the critical points where the derivative is equal to zero or undefined.
Setting f'(x) = 0:
1 - 5 / √(9 - x) = 0
5 / √(9 - x) = 1
(√(9 - x))^2 = 5^2
9 - x = 25
x = 9 - 25
x = -16.
The critical point is x = -16.
We can see that the derivative f'(x) is defined for all x values except x = 9, where the function is not differentiable due to the square root term.
Now, let's analyze the sign of the derivative f'(x) in the intervals (-∞, -16), (-16, 9), and (9, ∞).
For x < -16:
Plugging in a test value, let's say x = -17, into the derivative:
f'(-17) = 1 - 5 / √(9 - (-17))
= 1 - 5 / √(9 + 17)
= 1 - 5 / √26
≈ 1 - 0.97
≈ 0.03.
Since f'(-17) is positive, the function is increasing in the interval (-∞, -16).
For -16 < x < 9:
Plugging in a test value, let's say x = 0, into the derivative:
f'(0) = 1 - 5 / √(9 - 0)
= 1 - 5 / √9
= 1 - 5 / 3
≈ 1 - 1.67
≈ -0.67.
Since f'(0) is negative, the function is decreasing in the interval (-16, 9).
For x > 9:
Plugging in a test value, let's say x = 10, into the derivative:
f'(10) = 1 - 5 / √(9 - 10)
= 1 - 5 / √(-1)
= 1 - 5i,
where i is the imaginary unit.
Since the derivative is not a real number for x > 9, we cannot determine the sign.
Combining the information, we conclude that the function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
For more such questions on function, click on:
https://brainly.com/question/11624077
#SPJ8
A sphere has a volume of 7,234.56 units³. Using 3.14 for pi, find the radius of the sphere.
Answers
The radius of the sphere, rounded to two decimal places, is approximately 17.35 units.
To find the radius of the sphere, we can use the formula for the volume of a sphere:
V = (4/3)πr³,
where V represents the volume and r represents the radius of the sphere.
Given that the volume of the sphere is 7,234.56 units³, we can substitute this value into the formula:
7,234.56 = (4/3)(3.14)r³.
To solve for r, we can rearrange the equation:
r³ = (3/4)(7,234.56) / (3.14).r³ = 18,086.4 / 3.14.r³ ≈ 5,762.611.
Taking the cube root of both sides, we find:r ≈ 17.35.
For such more questions on Sphere:
https://brainly.com/question/20394302
#SPJ11
solve for x. log49^x=1/2
Answers
Answer:
x = 0.295
Step-by-step explanation:
1/5/2023
7:24PM
help me answer this please

Answers
Answer:
3,952 ft
Step-by-step explanation:
Use the sine function since you need to find the hypotenuse but know the opposite side of the angle, since sine is equal to opposite/hypotenuse.
sin8°=\(\frac{550}{c}\)
csin8°=550
c=550/sin8°
c= 3,952
please help me with these it is due tomm.

Answers
Answer:
1.) 10: 1, 2, 5, 10.
15: 1, 3, 5, 15,
Answer would be 5.
2.) 18: 1, 2, 3, 6, 9, 18
21: 1, 3, 7, 21
Answer would be 3.
3.) 12: 1, 2, 3, 4, 6, 12.
24: 1, 2, 3, 4, 6, 8, 12, 24.
Answer would be 12.
4.) 8: 1, 2, 4, 8.
20: 1, 2, 4, 5, 10, 20.
Answer would be 4.
5.) 14: 1, 2, 7, 14.
28: 1, 2, 4, 7, 14, 28.
Answer would be 14.
Step-by-step explanation:
Using the listing method, you would first list the common factors of each number, to which that number could be multiplied by. Then, you would search for the greatest common factor.
Amadi is three times as old as Chima. The sum of their ages is 24
Answers
Answer:
Amadi: 20 years old
Chima : 4 years old
Fred loves watermelon and buys 6 of them at the grocery store. If he gives friends 1 1/2 of a watermelon each, how many friends will get watermelon?
Answers
Answer:
4 friends will get watermelon
Step-by-step explanation:
1. 1 1/2 + 1 1/2 = 3
2. 1 1/2 + 1 1/2= 3
3. 3+3=6
4. Now count how many times we added 1 1/2.
5. If you counted correctly, you should've gotten 4.
Approximate -8+√20 to the nearest tenth. 4.5 3.5 -3.5 -4.5
Answers
Answer:
-8+√20 to the nearest tenth =-3.5
A circle has a radius of 30 cm and a central angle that measures 312 degrees. Find the length of the arc defined by this central angle
Answers
The length of the arc defined by the central angle of 312 degrees is 26π cm.
The formula for the arc length of a circle is given by:
L = (θ/360) × 2πr
where L is the length of the arc, θ is the central angle in degrees, and r is the radius of the circle.
Substituting the given values, we get:
L = (312/360) × 2π(30)
L = (26/30) × π × 30
L = 26π cm
Therefore, the length of the arc defined by the central angle of 312 degrees is 26π cm.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1
we know that a confidence interval for a population proportion is (0.22,0.40), with a margin of error of 0.09.
What is the sample proportion, p ?
Answers
P + 0.09 = 0.40
P - 0.09 = 0.22
Then P would equal 0.31 as 0.09 + 0.22 = 0.31, hope this helps :)) have a good day !
just give me a quick help on this

Answers
Answer:
I know you might be saying I am just taking the points, but I seriously can't see the question I will help you just put in the comments what the question is and I will help you!
a machinist is making a gear that will pull a chain at 60 ft/min when rotating at 40 rev/min. What should the radius of the gear be? Answer in inches.
Answers
The radius of the gear should be approximately 2.8644 inches.It is important to note that when making calculations involving units, we need to make sure that all units are consistent and convert them when necessary. In this case, we converted the answer from feet to inches to match the given unit.
To find the radius of the gear that will pull a chain at 60 ft/min when rotating at 40 rev/min, we can use the formula:
chain speed = 2 x pi x radius x rotational speed
where pi is a mathematical constant approximately equal to 3.14.
We know that the chain speed is 60 ft/min and the rotational speed is 40 rev/min, so we can substitute those values into the formula:
60 = 2 x 3.14 x radius x 40
Simplifying the equation, we get:
radius = 60 / (2 x 3.14 x 40)
radius = 0.2387 ft
To convert feet to inches, we can multiply the answer by 12:
radius = 0.2387 x 12 = 2.8644 inches.
For such more questions on Radius:
https://brainly.com/question/24375372
#SPJ11
PLEASE HELP ME!! ILL GIVE BRAINLIEST

Answers
Answer:
A, the first option, 49 square cm
Step-by-step explanation:
[] To know
-> A squares sides are all the same size
-> The area of a square can be found by finding L * W
[] Solving
-> We can use the points given to solve for one side, EF, of the square
-> Both the x coordinates are the same, so we can subtract the y values as they are on the same line.
6 - -1 = 6 + 1 = 7
-> Now for the area
7 * 7 = 49 square cm
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.
- Heather
estimate the value of -50 by plotting it on a number line
\( - \sqrt{50} \)
how to plot -50 on a number line
Answers
Answer:
Step-by-step explanation:
Never mind the minus for a second. What is the approximate value of sqrt(50)?
Isn't it about 7 or just a tiny bit over?
That's the answer here. Find the square root first, and then add the minus.
<o==o==o==o==o==o==o==o
-7 -6 -5 -4 - 3 - 2 - 1 0
In a school, 90% of the students enrolled online. If there are 1 500 students, how
many enrolled online?
Answers
90%+10%makes 100%
So then 1500-150= 1350
Answer:
1350 students
Step-by-step explanation:
90% of 1500 is 1350
Share £180 in the ratio 1:2:3.
Answers
Answer:
$30, $60 and $90
Step-by-step explanation:
The value of 1 unit: 180 : (1+2+3) = $60
30×1=$30
$30×2=$60
$30×3=$90
So $180 shared by the ratio 1:2:3 is $30, $60 and $90.
Answer: $30, $60 and $90.
Hope it helps you
Please solve this i really need this

Answers
Answer:
a = 8 (to nearest whole number)
Step-by-step explanation:
Given:
m<B = 36°
m<C = 104°
c = 12
Required:
a
SOLUTION:
✔️First find m<A:
m<A = 180 - (104 + 36)
m<A = 40°
✔️Find a using Sine Rule:
Thus:
\( \frac{a}{sin(A)} = \frac{c}{sin(C)} \)
Plug in the values
\( \frac{a}{sin(40)} = \frac{12}{sin(104)} \)
Multiply both sides by sin(40)
\( \frac{a}{sin(40)} * sin(40) = \frac{12}{sin(104)} * sin(40) \)
\( a = \frac{12*sin(40)}{sin(104)} \)
\( a = 8 \) (nearest whole number)
Angles P and Q are supplementary. m∠P=43∘. Which statement is true?
m∠Q=147∘
m∠Q=47∘
m∠Q=137∘
m∠Q=43∘
Answers
P + Q = 180
43 + Q = 180
Q = 180 - 43
m∠Q = 137°#CarryOnLearning
#LibreAngMatuto
Sep 27,
The midpoint of AB is M(-5,0). If the coordinates of A are (-8,5), what are the
coordinates of B?
Answers
Answer:
Step-by-step explanation:
(x-8)/2 = -5
x - 8 = -10
x = -2
(y+5)/2=0
y + 5 = 0
y = -5
(-2, -5)
300 feet above sea level??
Answers
Answer:
300
Step-by-step explanation:
if it is 300 feet ABOVE sea level, then it is a positive answer.
you would want to look for the words 'above' or 'below' if it is talking about sea level.
Quadratic Equations and Complex Numbers
please give a clear answer, thank you <3

Answers
The result of the given terms is -2/5 as per the given question from complex numbers.
What is a complex number?There is a multiplicative inverse for every nonzero complex number. As a result, complex numbers are a field with real numbers as a subfield. The complex numbers also form a two-dimensional real vector space with 1, I as the standard basis.
Because of this standard basis, the complex numbers form a Cartesian plane known as the complex plane. This allows for a geometric interpretation of complex numbers and operations, as well as the expression of geometric features and constructions in terms of complex numbers. Real numbers, for example, constitute the real line, which corresponds to the complex plane's horizontal axis.
=(((3/5)+(1/5)i)+((4/5)-(2/5)i) -((9/5)-(1/5)i))
=((3/5)+(4/5)-(9/5))-i((1/5)+i((1/5)-(2/5)+(1/5))
=(-2/5)+i(0)
= -2/5
Therefore, the result of the given terms is -2/5
To know more about complex number, visit:
https://brainly.com/question/20566728
#SPJ1
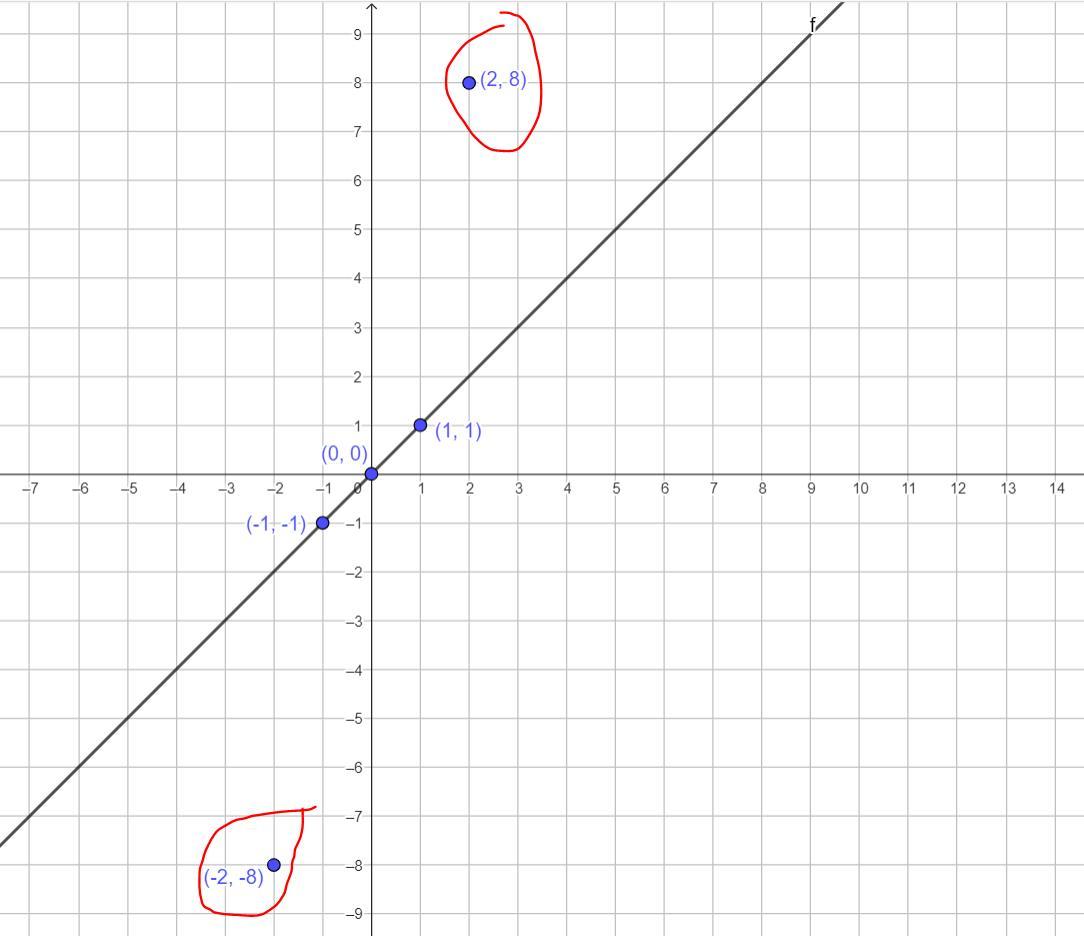
Choose the table or tables that represent a linear function.

Answers
Answer:
A and B
Step-by-step explanation:
You draw the points on the Cartesian plane and draw a straight line that passes through two of the drawn points, if ALL the drawn points are ON the drawn line, then it is a linear function,
If only ONE point lies outside the line, then it is NOT a linear function




Barney earns $24.75 in 3 hours if the amount that Barney earns varies directly with the number of hours, how much would he earn in 20 hours.
Answers
Answer:
$165
Step-by-step explanation:
Divide 24.75 by 3 to get how much Barney(lol) would get in a hour then I got 8.25 so 8.25 x 20 hours = $165
Answer:
165$ in 20 hours
Step-by-step explanation:
Barney earns 24.75 in 3 hours, so 24.75 / 3 is 8.25. This is every hour so you would take 8.25 and multiply it by 20. That gives you 165
you deposit $2,000 in an account that earns simple interest. after 6 months the account earns $210 in interest. what is the annual rate
Answers
Answer:
21%
Step-by-step explanation:
210 is 10.5% of the amount that is for 6 months doubling it will make it 420 that is 21% of the total amount of 2000.
1. Find the equation of the image of the circle x² + y2 + 16x-24y + 183 = 0 by rotated the line mirror 4x + 7y + 13 = 0. 2. The image of the circle (x - 3)² + (y-2)² = 1 in the line mirror ax + by = 19 is (x-1)³ + (y-16)2 = 1 then, find the values of (a, b). 3. Find the equation of a line passing through the origin and making an angle with the 4 line y-3x-5. 4. A parabola is drawn with its focus at (3,4) and vertex at the focus of the parabola y²-12x - 4y + 4 = 0. The n find equation of the parabola. 5. If the line ax + by + c = 0 touches the circle x² + y² - 2x = and is normal to the circle x² + y² + 2x - 4y + 1 = 0, then find the value of (a, b). 6. If the line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x. -3 7.1² 14 231= [] then find the matrix A 8. Find the equation of the ellipse having its center at the point (2,-3), one and one vertex at (4, -3). 3 9. Find the value of x if-1 0 10. Solve the linear system using Cramer's rule a) 2 1 2 4 (6x - 4y = -12 8x - 3y = -2 X = 16 -21 3x + 2y = z = 5 b) x-y+3z = -15 (2x + y +7z = -28 one focus at (3,-3) 11. Find the value of k for which the following system of linear equations has infinite solutions: x + (k+1)y = 5 ((k+1)x + 9y = 8k - 1
Answers
Answer:
-72x - 53y + 287 = 0.
Step-by-step explanation:
To find the equation of the image of the circle, we need to reflect each point on the circle in the given line mirror.
The line mirror equation is given as 4x + 7y + 13 = 0.
The reflection of a point (x, y) in the line mirror can be found using the formula:
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
where A, B, and C are the coefficients of the line mirror equation.
For the given line mirror equation 4x + 7y + 13 = 0, we have A = 4, B = 7, and C = 13.
Now, let's find the equations of the image of the circle.
The original circle equation is x² + y² + 16x - 24y + 183 = 0.
Using the reflection formulas, we substitute the values of x and y in the circle equation to find x' and y':
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
= (x - 2(4)y - 2(7)(4x + 7y + 13)) / (4^2 + 7^2)
= (x - 8y - 8(4x + 7y + 13)) / 65
= (x - 8y - 32x - 56y - 104) / 65
= (-31x - 64y - 104) / 65
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
= (y - 2(7)x + 2(4)(Ax + By + C)) / (4^2 + 7^2)
= (y - 14x + 8(Ax + By + C)) / 65
= (y - 14x + 8(4x + 7y + 13)) / 65
= (57x + 35y + 104) / 65
Therefore, the equation of the image of the circle is:
(-31x - 64y - 104) / 65 + (-57x + 35y + 104) / 65 + 16x - 24y + 183 = 0
Simplifying the equation, we get:
-31x - 64y - 57x + 35y + 16x - 24y + 183 + 104 = 0
-72x - 53y + 287 = 0
So, the equation of the image of the circle is -72x - 53y + 287 = 0.
Question 8 (1 point)
A real estate agent received a 5.5% commission on the sale of a home. If her
commission was $14,960, how much did the home sell for?
Answers
The amount of the sale of the home is $2090181.82
How to determine how much the home sells for?From the question, we have the following parameters that can be used in our computation:
Commission = 5.5% on the sale of a home
Also, we have
Commission = 114960
using the above as a guide, we have the following:
5.5% on the sale of a home = 114960
So, we have
5.5% * sale of a home = 114960
Divide both sides by 5.5%
sale of a home = 114960/(5.5%)
Evaluate
sale of a home = 2090181.82
Hence, the sale of the home is $2090181.82
Read more about commission at
https://brainly.com/question/26283663
#SPJ1
As part of a larger experiment, Dale (1992) looked at six samples of a wetland soil undergoing a simulated snowmelt. Three were randomly selected for treatment with a neutral pH snowmelt; the other three got a reduced pH snowmelt. The observed response was the number of Copepoda removed from each microcosm during the first 14 days of snowmelt Reduced pH Neutral pH 256 159 149 54 123 248 (a) [3 points Write two simple models: one model for the number of Copepoda in a neutral pH snowmelt and one model for the number of Copepoda in a reduced pH snowmel. Use mathematical notations. (b) 2 points We want to test whether the two treatments have equal average numbers of Copepoda. Write the n and the alternative hypotheses using the notations defined in the previous question (c) 5 points We want to perform a t-test. What assumptions are you making? Compute the corresponding test statistic. Give the critical value for a level of significance v = 0.05. What do you conclude? (d) 5 points) Using a randomization-based analysis, test the nul hypothesis that the two treatments have equal average numbers of Copepoda versus a two-sided alternative. Use a level of significance v = 0.05.
Answers
(a) The mathematical notations is (xₙ, yₙ)
(b) The alternative hypotheses using the notations defined in the previous question is t = (Xₙ - Yₙ) / SE
(c) The assumptions making is variances of the two populations are equal.
A hypothesis is a tentative explanation or prediction of a phenomenon, and it is essential in scientific research. In this study, we have two hypotheses:
Null Hypothesis: There is no significant difference in the average number of Copepod between the reduced pH and neutral pH snowmelt treatments.
Alternative Hypothesis: There is a significant difference in the average number of Copepod between the reduced pH and neutral pH snowmelt treatments.
Model:
A model is a mathematical representation of a phenomenon, and it is used to make predictions or explanations. In this experiment, we can create two simple models:
Model for Neutral pH Snowmelt:
Let Yₙ be the number of Copepod in a microcosm treated with neutral pH snowmelt. Then, Yₙ follows a normal distribution with mean µn and standard deviation σn.
Model for Reduced pH Snowmelt:
Let Yₙ be the number of Copepod in a microcosm treated with reduced pH snowmelt. Then, Yₙ follows a normal distribution with mean µr and standard deviation σr.
Assumptions:
Before conducting a t-test, we must ensure that the data satisfies the following assumptions:
The sample is a random and representative sample of the population.
The data is normally distributed.
The variances of the two populations are equal.
The test statistic for the t-test is:
t = (Xₙ - Yₙ) / SE
where Xₙ is the sample mean of neutral pH snowmelt, Yₙ is the sample mean of reduced pH snowmelt, and SE is the standard error.
Assuming a level of significance v = 0.05, we have a critical value of t = 2.306 for a two-tailed test with 4 degrees of freedom. If our calculated t-value is greater than 2.306 or less than -2.306, we reject the null hypothesis.
We can perform a randomization test as follows:
If the p-value is less than 0.05, we reject the null hypothesis and conclude that there is a significant difference in the average number of Cope pod between the reduced pH and neutral pH snowmelt treatments. If the p-value is greater than 0.05, we fail to reject the null hypothesis.
To know more about hypothesis here.
https://brainly.com/question/29576929
#SPJ4
There is a line whose slope is 2 and whose slope is 2 and whose y- intercept is 8. What is its equation in slope-intercept form?