How many solutions does this equation have?
–20 − 5s = –5s + 6 − 12
Answers
Answer:
No Solution
Step-by-step explanation:
-20 - 5s = -5s + 6 - 12
+ 5s +5s
________________
-20 = 6 - 12
-20 = -6
Both sides aren't equal to each other, so there's no solution for "s" to make both sides of the equation true.
Related Questions
Need to generate a recursive formula to the story problem given below. Give the recursive equation at the top of your answer (do not forget your base case(s)) and then show your thought process after. Question: How many n-letter "words" can be created from an unlimited supply of a’s, b’s, and c’s, if each word MUST contain an even number of a’s?
Answers
The recursive formula for the given problem is W(n) = W(n-1) + 2 * W(n-1), with the base case W(0) = 1. This formula calculates the number of n-letter "words" that can be created from an unlimited supply of 'a's, 'b's, and 'c's,
To derive the recursive formula, we consider two cases for the first letter of the word: either it is an 'a' or it is not. If the first letter is 'a', we need to ensure that the remaining (n-1) letters form a word with an even number of 'a's. Therefore, the number of words in this case is equal to W(n-1), as we are recursively solving for the remaining letters.
If the first letter is not 'a', we have the freedom to ch
oose from 'b' or 'c'. In this case, we have two options for each of the remaining (n-1) letters, resulting in 2 * W(n-1) possibilities. By summing these two cases, we obtain the recursive formula W(n) = W(n-1) + 2 * W(n-1), which calculates the total number of n-letter words satisfying the given criteria.
To learn more about recursive formulas click here :
brainly.com/question/1470853
#SPJ11
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
2. (a) Find the derivative y. given:
(i) y = (x^2 + 1) arctan x - x
(ii) y = sinh(xlogx ).
(b) Using logarithmidifferentiation, find y' if y=x^2 4^(x^2) + cosh^6 3x..
Answers
a) (i)\(y' = (x^2 + 1)/(1 + x^2) + 2x * tan^{-1}(x) - 1\) (ii) y' = sinh(xlogx) * [1 + log(x)] b)\(y' = [x^2 * 4^{x^2} + cosh^6(3x)] * [2/x + 2xln(4) + 6cosh^5(3x) * sinh(3x) * 3]\) are the derivatives
(a) Finding the derivatives:
(i) To find the derivative of \(y = (x^2 + 1) tan^{-1}(x) - x,\) we can use the product rule and the chain rule. Let's calculate it step by step:
Using the product rule:
\(y' = [(x^2 + 1) * d(tan^{-1}(x))/dx] + [tan^{-1}(x) * d(x^2 + 1)/dx] - 1\)
Using the chain rule:
\(y' = [(x^2 + 1) * (1/(1 + x^2))] + [tan^{-1}(x) * 2x] - 1\)
Simplifying:
\(y' = (x^2 + 1)/(1 + x^2) + 2x * tan^{-1}(x) - 1\)
(ii) To find the derivative of y = sinh(xlogx), we can use the chain rule. Let's calculate it step by step:
Using the chain rule:
y' = d(sinh(xlogx))/dx * d(xlogx)/dx
Using the chain rule again for the second term:
y' = sinh(xlogx) * [d(xlogx)/dx]
Simplifying:
y' = sinh(xlogx) * [x * (1/x) + log(x)]
Simplifying further:
y' = sinh(xlogx) * [1 + log(x)]
(b) Using logarithmic differentiation, find y' if \(y = x^2 * 4^{x^2} + cosh^6(3x):\)
Let's take the natural logarithm of both sides of the equation:
\(ln(y) = ln(x^2 * 4^{x^2} + cosh^6(3x))\\Now, differentiate implicitly with respect to x:\\(d/dx) ln(y) = (d/dx) ln(x^2 * 4^{x^2} + cosh^6(3x))Using the logarithmic differentiation rule:\\y' / y = [(2x/x^2) + (d/dx)(x^2) * ln(4) + (d/dx)(cosh^6(3x))]Simplifying:\\y' / y = [2/x + 2xln(4) + 6cosh^5(3x) * (d/dx)(cosh(3x))]\\Using the chain rule for the last term:\\y' / y = [2/x + 2xln(4) + 6cosh^5(3x) * sinh(3x) * 3]Now, multiply both sides by y:\\\)
\(y' = y * [2/x + 2xln(4) + 6cosh^5(3x) * sinh(3x) * 3]Replace y with the original expression:\\\y' = [x^2 * 4^{x^2} + cosh^6(3x)] * [2/x + 2xln(4) + 6cosh^5(3x) * sinh(3x) * 3]\)
This is the derivative of y using logarithmic differentiation.
Learn more about derivative here:
https://brainly.com/question/25324584
#SPJ4
The side length, s, of a cube is 4x2 3. if v = s3, what is the volume of the cube? 64x6 144x4 108x2 27 64x6 48x4 12x2 1 4x6 36x4 108x2 27 4x6 12x4 12x2 1
Answers
The volume of the cube given the dimensions of the side length is \(64x^{6} + 144x^{4} + 108x^{2} + 27\)
What is the volume of the cube?A cube is a 3-dimensional object that has six faces, twelve edges and eight vertices.
Volume of a cube = a³
Where a = length of a side
(4x² + 3) × (4x² + 3) = 16x^4 + 24x² + 9
(16x^4 + 24x² + 9) × (4x² + 3) = \(64x^{6} + 144x^{4} + 108x^{2} + 27\)
To learn more about the volume of a cube, please check: https://brainly.com/question/26406747
#SPJ5
Solve for x.
23=79(6x−36)+9
Enter your answer in the box.
x =
Answers
Answer:
x= 6.02953586.......
Step-by-step explanation:
In a sample of 400 voters, 360 indicated they favor the incumbent governor. The 95% confidence interval of voters not favoring the incumbent is
Answers
The 95% confidence interval of voters not favoring the incumbent is (0.0706, 0.1294).
Sample size, n=400
Sample proportion, p = 40 / 400
= 0.1
We use normal approximation, for this, we check that both np and n(1-p) >5.
Since n*p = 40 > 5 and n*(1-p) = 360 > 5, we can take binomial random variable as normally distributed, with mean = p = 0.1 and standard deviation = root( p * (1-p) /n )
= 0.015
For constructing Confidence interval,
Margin of Error (ME) = z x SD = 0.0294
95% confidence interval is given by Sample Mean +/- (Margin of Error)
0.1 +/- 0.0294 = (0.0706 , 0.1294)
Learn more about Margin of Error here https://brainly.com/question/15691460
#SPJ4
What is the slope of a line perpendicular to the line on the graph?

Answers
Answer:
1/2
Step-by-step explanation:
slope of perpendicular lines are always negative reciprocal of each other.
so slope of the given line = rise over run
that means -2/1 = -2
so slope of a line that is perpendicular to it will be negative of its reciprocal
that will be
\( \frac{1}{2} \)
PLEASE HELP
What two-dimensional cross-sections could be obtained from a right rectangular prism?

Answers
The two-dimensional cross-sections that can be obtained from a right rectangular prism is a rectangle.
What is a prism?A prism is a 3-dimensional shape with two identical shapes called bases facing each other. The other faces of a prism are parallelograms or rectangles.
The two-dimensional cross-sections that can be obtained from a right rectangular prism is a rectangle.
Find out more on prism at: https://brainly.com/question/23963432
#SPJ1
52. How many terms are in the
following expression?
5a +3002 anion
A.
1
B. 2
C. 3
. D. O
02.12.2
10.
DO
5
6.EE

Answers
Answer:
2 terms
Step-by-step explanation:
terms include the coefficient and the variables
Answer:
2
Step-by-step explanation:
5a can be considered a term with a variable and 3 can be considered constant term, therefore 2 terms
hopefully this answer helped you!!!
Suppose x has a distribution with = 30 and = 28.
(a) If a random sample of size n = 31 is drawn, find x, x and P(30 ≤ x ≤ 32). (Round x to two decimal places and the probability to four decimal places.)
x =
x =
P(30 ≤ x ≤ 32) =
(b) If a random sample of size n = 62 is drawn, find x, x and P(30 ≤ x ≤ 32). (Round x to two decimal places and the probability to four decimal places.)
x =
x =
P(30 ≤ x ≤ 32) =
(c) Why should you expect the probability of part (b) to be higher than that of part (a)? (Hint: Consider the standard deviations in parts (a) and (b).)
The standard deviation of part (b) is ---Select--- larger than the same as smaller than part (a) because of the ---Select--- same smaller larger sample size. Therefore, the distribution about x is ---Select--- narrower the same wider .
Answers
a) P(30 ≤ x ≤ 32) = 0.3446.
b) P(30 ≤ x ≤ 32) = 0.2868.
c) The probability of getting values between 30 and 32 for x is higher in part (b) than in part (a).
We have,
(a)
The mean of the distribution is = 30 and the standard deviation is = 28.
For a sample size n = 31, the sample mean x follows a normal distribution with mean = 30 and standard deviation = /√n = 28/√31 = 5.02 (approx.).
Therefore, x ~ N(30, 5.02).
The probability P(30 ≤ x ≤ 32) can be found by standardizing the values using the formula z = (x - ) / , where z is the standard normal variable.
z1 = (30 - 30) / 5.02 = 0
z2 = (32 - 30) / 5.02 = 0.40
P(30 ≤ x ≤ 32) = P(0 ≤ z ≤ 0.40) = 0.3446 (approx.)
Therefore, x = 30, x = 5.02, and P(30 ≤ x ≤ 32) = 0.3446 (approx.).
(b)
For a sample size n = 62, the sample mean x follows a normal distribution with mean = 30 and standard deviation = /√n = 28/√62 = 3.56 (approx.).
Therefore, x ~ N(30, 3.56).
The probability P(30 ≤ x ≤ 32) can be found using the same method as in part (a).
z1 = (30 - 30) / 3.56 = 0
z2 = (32 - 30) / 3.56 = 0.56
P(30 ≤ x ≤ 32) = P(0 ≤ z ≤ 0.56) = 0.2868 (approx.)
Therefore, x = 30, x = 3.56, and P(30 ≤ x ≤ 32) = 0.2868 (approx.).
(c)
The standard deviation of part (b) is smaller than part (a) because of the larger sample size.
Therefore, the distribution about x is narrower in part (b) than in part (a). This means that the sample mean x in part (b) is likely to be closer to the population mean than the sample mean x in part (a).
As a result, the probability of getting values between 30 and 32 for x is higher in part (b) than in part (a).
Thus,
a) P(30 ≤ x ≤ 32) = 0.3446.
b) P(30 ≤ x ≤ 32) = 0.2868.
c) The probability of getting values between 30 and 32 for x is higher in part (b) than in part (a).
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ11
Divisibility rules with algebra

Answers
Answer:
D=8
Step-by-step explanation:
normal division rules
33 goes into 47 1 time
then it leaves 17D
if we divide 170 by 33, we get 5 and if we divide 179 by 33, we still get 5. So we have 17D-165. That leaves us with something that you multiply 33 with to have a 2 in the ones place so that you get a remainder of 2. (In order to get 2 in the remainder, we need a 2 in the ones place because 4-2=2. In order to get that we need to see which number multiplied with 33 would get us a number smaller than 179 but also has a 2 in the ones place. Theres only one number and thats 4. 33*4=132. So in order to get only 2 in the remainder, we need the rest to be subtracted. This means that 17D-165=134. This way we can see that D=8
I need help pls what’s the answer I need it asap?

Answers
The inverse of the matrix \(\left[\begin{array}{cc}2&-7\\-2&5\end{array}\right]\) is \(-\frac 14 \left[\begin{array}{cc}5&7\\2&2\end{array}\right]\)
Calculating the inverse of the matrixFrom the question, we have the following parameters that can be used in our computation:
\(\left[\begin{array}{cc}2&-7\\-2&5\end{array}\right]\)
The determinant (D) of the matrix is
D = 2 * 5 + 7 * -2
Evaluate
D = -4
The inverse, I is then calculated as
\(I = -\frac 14 \left[\begin{array}{cc}5&7\\2&2\end{array}\right]\)
Read more about matrix at
https://brainly.com/question/11989522
#SPJ1
If "C" is the total cost in dollars($) to produce q units of a product, then the average cost per unit for an output of q units is given by c = c/q Thus if the total cost equation is c = 5000 + 6q, then c = 5000/q + 6 given that the fixed cost is $12,000 and the variable cost is given by the function cv = 7q
Answers
Thus, the average cost per unit for an output of q units is given by the equation c/q = 12000/q + 7, where the fixed cost is $12,000 and the variable cost is given by the function cv = 7q.
The given equation for the total cost of producing q units of a product is c = 5000 + 6q.
To find the average cost per unit for an output of q units, we need to divide the total cost by the number of units produced.
Thus, the average cost per unit can be written as c/q.
Substituting the given equation for c in terms of q, we get
c/q = (5000 + 6q)/q.
Simplifying this expression, we get c/q = 5000/q + 6.
Now, we are given that the fixed cost is $12,000 and the variable cost is given by the function cv = 7q.
The total cost equation c can be written as the sum of the fixed cost and the variable cost, i.e., c = 12000 + cv. Substituting the given equation for cv, we get c = 12000 + 7q.
Substituting this equation for c in terms of q in the expression we derived earlier for c/q, we get c/q = (12000 + 7q)/q. Simplifying this expression, we get c/q = 12000/q + 7.
Therefore, the average cost per unit for an output of q units is given by the equation c/q = 12000/q + 7, where the fixed cost is $12,000 and the variable cost is given by the function cv = 7q.
Know more about the average cost
https://brainly.com/question/29509552
#SPJ11
A straight line has gradient 4 and passes through the point (5,23).
Work out the equation of the line.
Answers
Answer:
Equation of line is: \(\mathbf{y=4x+3}\)
Step-by-step explanation:
We are given:
A straight line has gradient 4 and passes through the point (5,23).
Work out the equation of the line.
The equation of line will be in slope-intercept form: \(y=mx+b\)
where m is slope and b is y-intercept
Finding slope
We have slope (gradient) m = 4
Finding y-intercept
Using slope m = 4 and point (5,23) we can find b i.e y-intercept
\(y=mx+b\\23=4(5)+b\\23=20+b\\b=23-20\\b=3\)
So, we get y-intercept b = 3
Finding Equation of Line
Now, writing equation of line having slope m = 4 and y-intercept b = 3 is:
\(y=mx+b\\y=4x+3\)
So, the Equation of line is: \(\mathbf{y=4x+3}\)
x²-y²+x-y=0
can yall solve this is either or format
Answers
y-intercept: (0,0) (0, -1)
Help!!!
a $52 item is marked up 10% and then markdown 10% what is the final price
Answers
Answer: $51.48
Step-by-step explanation:
If a $52 item is marked up by 10%, its new price will be:
$52 + 10% of $52 = $52 + $5.20 = $57.20
Then, if this new price is marked down by 10%, the final price will be:
$57.20 - 10% of $57.20 = $57.20 - $5.72 = $51.48
Therefore, the final price of the item after the markup and markdown is $51.48.
HELP ME 7th grade math
What is the total surface area?

Answers
Answer:
Step-by-step explanation:
To calculate the total surface area, you first need to calculate the surface area of one of the 4 triangles and multiply that by 4.
We can solve this two ways (I would recommend using 2).
1)
Using herons formula:
a, b, c = different sides of the triangle (length)
s = (a + b + c) / 2
a = \(\sqrt{s(s-a)(s-b)(s-c)}\)
If we input values:
a = b = c = 6.5m
s = (3 * 6.5) / 2 = 9.75
\(\sqrt{s(s-6.5)^{3} }\) which is about 18.29478 (exact answer: \(3.25\sqrt{31.6875}\))
18.29478 * 4 = the entire area = 73.17912 m^2
exact whole area: \((13\sqrt{31.6875})m^{2}\)
2)
Each of the four triangles can be divided into 2 more triangles.
(2 * 4 = 8 = total amount of new small triangles)
How we calculate the area of one of the new small ones:
(h * w) / 2 = a
h = 5.6m
w = (width of one of the four triangles width divided by 2) = 3.25m
3.25m * 5.6m = 18.2m^2
18.2m^2 / 2 = 9.1m^2
There are 8 of the new small triangles in the biggest triangle made up of four smaller ones.
So if we take 9.1m^2 * 8, we get the total area!
Total area: 72.8m^2
Happy to help you!
If you have any questions, ask in the comments below!
Have a good day! (●'◡'●)
if alpha and beta are zeroes of x2-3x+q. what is the value of q, if 2 alpha+3 beta=15
Answers
The value of q is -27.
Recall Vieta's Formulas, which state that for a quadratic equation \(ax^2\) + bx + c = 0 with zeroes alpha and beta, the sum of the zeroes is equal to -b/a, and the product of the zeroes is equal to c/a.
In our equation \(x^2\) - 3x + q, the sum of the zeroes alpha and beta is -(-3)/1 = 3.
We are given that 2 alpha + 3 beta = 15. Substitute alpha = (15 - 3 beta)/2 into the equation.
Replace the value of alpha in the sum of zeroes equation: (15 - 3 beta)/2 + beta = 3.
Simplify the equation by multiplying both sides by 2: 15 - 3 beta + 2 beta = 6.
Combine like terms: 15 - beta = 6.
Subtract 15 from both sides: -beta = -9.
Multiply both sides by -1 to solve for beta: beta = 9.
Substitute the value of beta into the sum of zeroes equation: alpha = (15 - 3 * 9)/2 = -3.
Since we have the values of alpha and beta, we can find q using the product of the zeroes formula: q = alpha * beta = -3 * 9 = -27.
For more such questions on value, click on:
https://brainly.com/question/843074
#SPJ8
The Marcos family consists of 2 adults and 4 children. They spent a total of $40 on circus tickets. Let x represent the cost of an adult ticket, and let y represent the cost of a child’s ticket. Which graph represents the possible costs of the tickets?
On a coordinate plane, a line goes through points (0, 10) and (20, 0).
On a coordinate plane, a line goes through points (0, 20) and (10, 0).
On a coordinate plane, a line goes through points (negative 10, 0) and (0, 20).
On a coordinate plane, a line goes through points (negative 20, 0) and (0, 10).
Answers
Answer:
First Option
Step-by-step explanation:
First, we will find the equation for the total cost of the tickets.
Given x = Cost of 1 adult ticket
y = Cost of 1 Child ticket
Total Cost of tickets at $40:
2x + 4y = 40
To find which graph represent the cost of the tickets,
we can substitute x = 0 to find y and vice-versa.
If x = 0 ,
\(2(0) + 4y = 40\\4y = 40\\y = \frac{40}{4} \\= 10\)
So when x = 0 , y = 10 which gives the coordinates (0,10).
Now if y = 0,
\(2x+4(0) = 40\\2x = 40\\x = \frac{40}{2} \\= 20\)
So when y = 0 , x = 20 which gives the coordinates (20,0)
This shows that this particular line passes through these 2 points and therefore the answer is the first option.
Answer: A i just took the test
Step-by-step explanation:
What's 0.016 as a fraction
Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: 2/125
Explanation:
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer:
16/1,000
Understanding place values:
The first 0 before the decimal point in 0.016 represents ones, the 0 after the decimal point represents tenths, the 1 represents hundredths and the 6 represents thousandths. We use 1,000 in our fraction because of the place value.
Step-by-step explanation:
1. Convert 0.016 into a fraction:
0.016 = 16/1,000
2. Simpilfy the fraction 16/1,000:
16/1,000 ÷ 8 = 2/125
2/125 is equivalent to 0.016
Side Note: Step 2. is only for people looking for the simplified answer!
~Hope this helps!
~Hocus Pocus
A french fries stand offers both curly and straight fries. These can be topped with any combination of five available sauces. How many combinations are possible?
Answers
How many solutions are there to the inequality x1 + x2 + x3 ≤ 11, where x1, x2, and x3 are nonnegative integers? [Hint: Introduce an auxiliary variable x4 such that x1 + x2 + x3 + x4 = 11.]
Answers
The number of nonnegative integer solutions to the inequality x1 + x2 + x3 ≤ 11 is C(14,3) = 364.
We can solve this inequality by introducing an auxiliary variable x4, such that x1 + x2 + x3 + x4 = 11. Here, x1, x2, x3, and x4 are all nonnegative integers.
We can interpret this equation as follows: imagine we have 11 identical objects and we want to distribute them among four boxes (x1, x2, x3, and x4). Each box can contain any number of objects, including zero. The number of solutions to this equation will give us the number of nonnegative integer solutions to the original inequality.
We can use a technique known as stars and bars to count the number of solutions to this equation. Imagine we represent the 11 objects as stars: ***********.
We can then place three bars to divide the stars into four groups, each group representing one of the variables x1, x2, x3, and x4. For example, if we place the first bar after the first star, the second bar after the third star, and the third bar after the fifth star, we get the following arrangement:
| ** | * | ****
This arrangement corresponds to the solution x1=1, x2=2, x3=1, and x4=7. Notice that the number of stars to the left of the first bar gives the value of x1, the number of stars between the first and second bars gives the value of x2, and so on.
We can place the bars in any order, so we need to count the number of ways to arrange three bars among 14 positions (11 stars and 3 bars). This is equivalent to choosing 3 positions out of 14 to place the bars, which can be done in C(14,3) ways.
Therefore, the number of nonnegative integer solutions to the inequality x1 + x2 + x3 ≤ 11 is C(14,3) = 364.
Click the below link, to learn more about solutions of the inequality :
https://brainly.com/question/22010462
#SPJ11
Name the polynomial based on its degree and number of terms x4+2
Answers
Based on its degree, and the number of terms, the polynomial is named as: bi-quadratic binomial.
What is a Binomial?A binomial is a type of polynomial that has two unrelated terms or unlike terms, having subtraction or addition sign separating the two terms. For example, the polynomial, ax² - b, has two unlike terms, ax² and b, and is therefore called a polynomial.
What is a Bi-quadratic Polynomial?A bi-quadratic polynomial can be defined as a type of polynomial that has the term with the highest degree as 4. For example, the polynomial, ax^4 - b, is a bi-quadratic polynomial because the term that has the highest degree as 4 is ax^4.
Given the polynomial, x^4 + 2:
There are two terms, x^4 and 2
The highest degree is 4.
Therefore, based on its degree, the polynomial is named as: a bi-quadratic polynomial.
Based on the number of terms, the polynomial is named as: a binomial polynomial.
It can be named as: bi-quadratic binomial.
Learn more about a bi-quadratic binomial on:
https://brainly.com/question/21691794
#SPJ1
6.The base of an isosceles triangle is 6 cm and its perimeter is 16 cm. Length of each of the equal sides is
Answers
Answer:
erm
Step-by-step explanation:
The sides will be:
6cm
6cm
4cm
Answer:
In isosceles triangle two sides are equal . Let the length be x .hence perimeter can be given as x + x + 6 . Therefore 2x + 6 = 16 . And 2x = 10 .and hence x =5 . So the length of each side is 5 cm
Step-by-step explanation:
Point E is located at (-8,7). Point F is located at (9,7).
What is the distance, in units, between point E and point F?
Answers
Answer:
18 units to the right.
Step-by-step explanation:
Hope this helps!
a bucket that weighs 4 pounds and a rope of negligible weight are used to draw water from a well that is 83 feet deep. the bucket is filled with 35 pounds of water and is pulled up at a rate of 1.8 feet per second, but water leaks out of a hole in the bucket at a rate of 0.25 pounds per second. find the work done pulling the bucket to the top of the well. your answer must include the correct units. (you may enter lbf or lb*ft for ft-lb.)
Answers
The work done pulling the bucket to the top of the well is 104,299.4 pound-force-feet (lb*ft).
To find the work done pulling the bucket to the top of the well, we need to consider the weight of the bucket, the weight of the water, and the work done against gravity.
First, let's calculate the weight of the bucket and water combined. The weight of the bucket is 4 pounds, and the weight of the water is 35 pounds. Therefore, the total weight is 4 + 35 = 39 pounds.
Next, let's calculate the distance the bucket is pulled up. The well is 83 feet deep, so the bucket is pulled up a distance of 83 feet.
Now, let's calculate the work done against gravity. Work is calculated by multiplying the force applied by the distance over which the force is applied. In this case, the force is equal to the weight of the bucket and water, which is 39 pounds. The distance is 83 feet.
Work = Force * Distance
Work = 39 pounds * 83 feet
To calculate the work, we need to convert the weight from pounds to a unit called pound-force (lbf). 1 pound force is equal to the force exerted by a mass of 1 pound under acceleration due to gravity.
To convert from pounds to pound-force, we need to multiply by the acceleration due to gravity. The acceleration due to gravity is approximately 32.2 feet per second squared.
39 pounds * 32.2 feet per second squared = 1255.8 pound-force
Finally, we can calculate the work done pulling the bucket to the top of the well.
Work = 1255.8 pound-force * 83 feet
Work = 104,299.4 pound-force-feet (or lb*ft)
Learn more about the work done:
https://brainly.com/question/28356414
#SPJ11
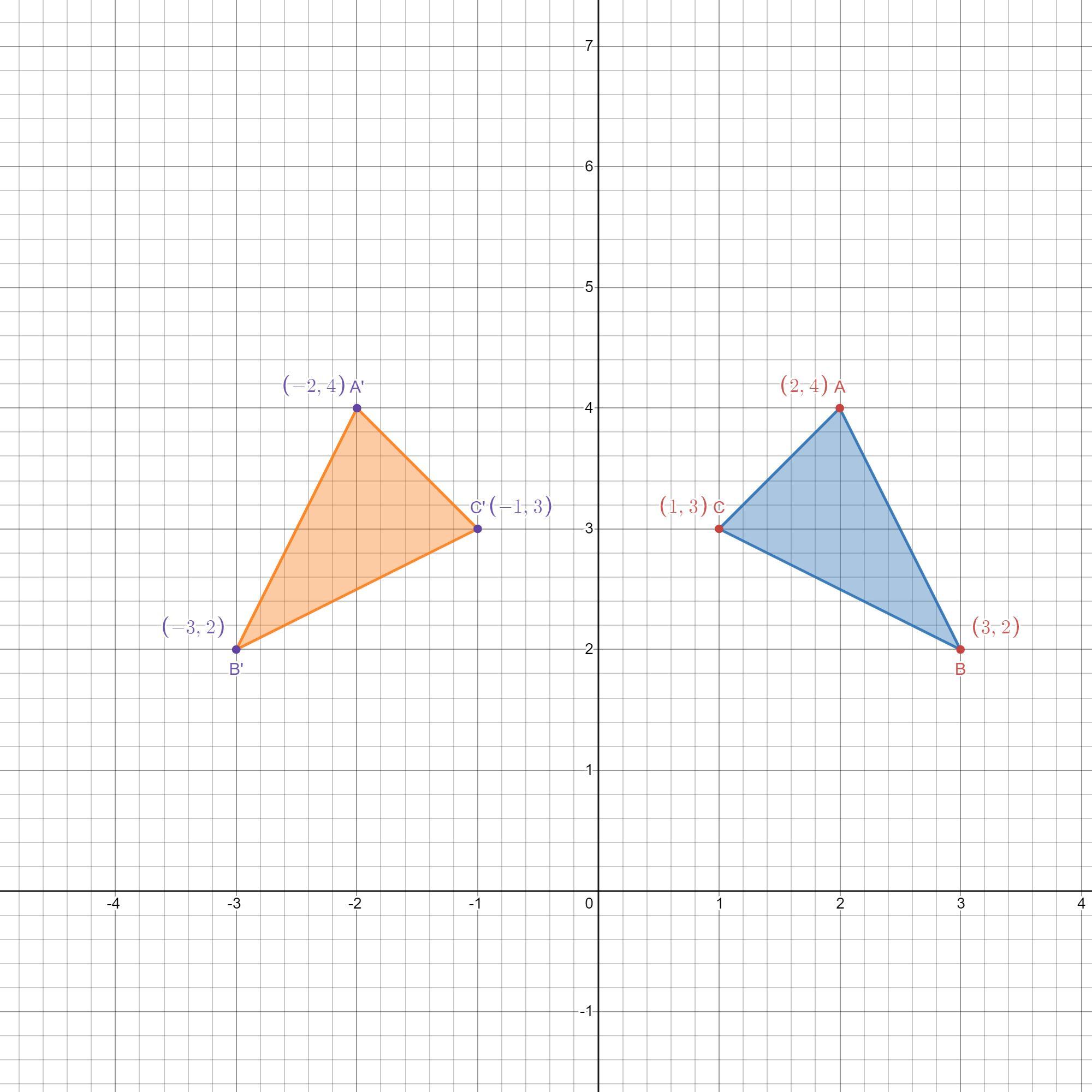
What are the coordinates of point B' after
AABC is reflected across the y-axis?
5 y
А
В'
?
?
с
B (3,2
-5
0
-5

Answers
Answer:
B'(-3, 2)
Step-by-step explanation:
The rule for a reflection over the y-axis is (x, y) → (-x, y)
This means that the x-values change while the y-values stay the same.
B(x, y) → (-x, y)
B(3, 2) → (-3, 2)
B'(-3, 2)
Hope this helps!
what is always true about a line that Slants downward from left to right select all that apply help plz
Answers
Answer:
A line that slants down from left to right has a negative slope. Horizontal and vertical lines also have a slope.
Step-by-step explanation:
Get 100 points for absolutely nothing thank me later
Answers
Answer:
thanks
Step-by-step explanation:
Answer:
Thank you so much !
You're the best :)
Una escuela debe transportar 200 estudiantes a un evento. Hay disponibles
tanto autobuses grandes como pequeños. Un autobús grande tiene
capacidad para 50 personas y alquilarlo para el evento cuesta $800. Un
autobús pequeño tiene capacidad para 40 personas y alquilarlo para el
evento cuesta $600. Hay 8 conductores disponibles el día del evento.
* Encuentra la combinación de autobuses que puedan transportar a los 200 estudiantes al menor costo posible utilizando no más de 8 conductores.
• Escribe la función objetivo y cuantifique las restricciones como desigualdades.
• Verifica que el problema se puede resolver utilizando la programación lineal.
• Grafica el sistema de desigualdades lineales. Identifique la región viable y los vértices.
• Sustituye los vértices en la función objetivo para determinar las soluciones que brindan la
solución mínima o máxima.
• Interpreta la solución en términos de otras variables de decisión
Answers
The combination of buses that can transport the 200 students at the lowest possible cost using no more than 8 drivers is 3 large buses and 2 small buses, at a total cost of $3,600.
Let's start by using just large buses. We would need 4 buses to transport all 200 students, at a cost of $3,200 (4 buses x $800 per bus). However, this would require 4 drivers, leaving only 4 drivers available for any additional buses.
Next, let's try using just small buses. We would need 5 buses to transport all 200 students, at a cost of $3,000 (5 buses x $600 per bus). This would also require 5 drivers, leaving only 3 drivers available for any additional buses.
Now, let's try a combination of large and small buses. Let's start with 3 large buses and 1 small bus. This would transport 190 students (3 buses x 50 seats + 1 bus x 40 seats), leaving 10 students who would need to be transported on another small bus. The total cost for this combination would be $3,000 (3 large buses x $800 per bus + 1 small bus x $600 per bus).
We still have 7 drivers remaining, so let's add another small bus to transport the remaining 10 students. This would bring the total cost to $3,600 (3 large buses x $800 per bus + 2 small buses x $600 per bus).
Learn more about the combination
https://brainly.com/question/19692242
#SPJ4
Translate Question: A school must transport 200 students to an event. Both large and small buses are available. A large bus holds 50 people and costs $800 to rent for the event. A small bus holds 40 people and costs $600 to rent for the event. There are 8 drivers available on the day of the event. *
Find the combination of buses that can transport the 200 students at the lowest possible cost using no more than 8 drivers. •