Answers
Answer:
The 1/4th power means the 4th root of a number.
Therefore for the first question, the answer should be 4th root of 1296 -4th root of 625. or \sqrt[4]{1296}
4
1296
-\sqrt[4]{625}
4
625
:D
For the second question just calculate? what to the 4th power is 1296 and what to the 4th power is 625?
They should respectively be 6 and 5. So the final answers we get is 6-5=1
If you have any questions about this just ask me in the comment and I will get to it as soon as I could.
hopecthis helps
Related Questions
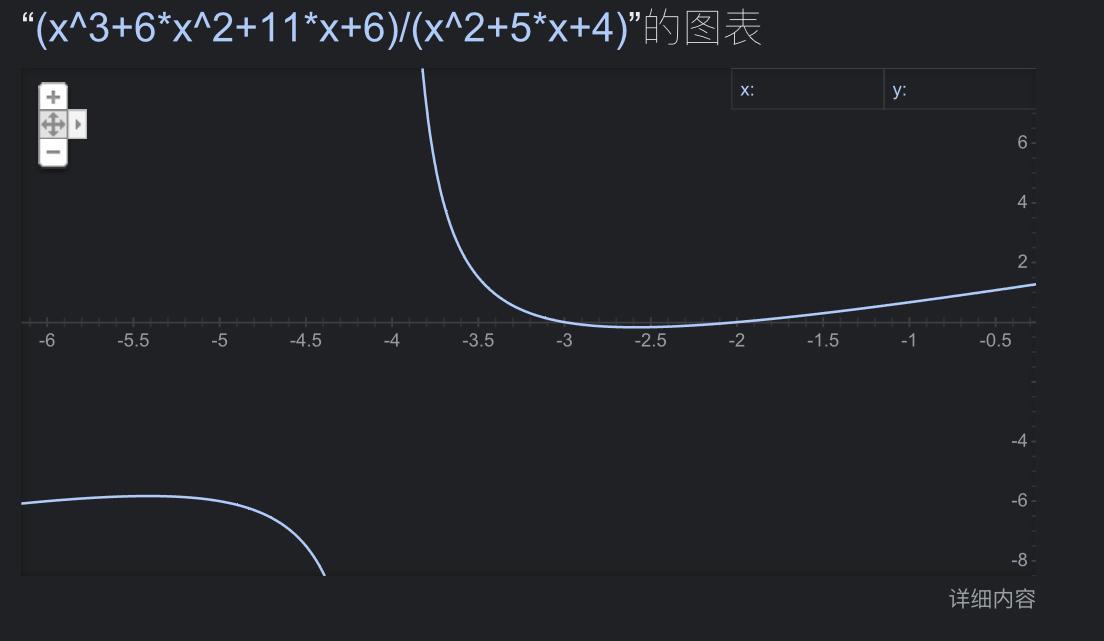
How do you do (x^3 + 6x^2 +11x +6) / (x^2 + 5x + 4) in long division?
Answers
Answer:see the photo I send to you
Step-by-step explanation:
Ok

If it is true that z^2-6=19 then z^2+6=
Answers
Answer:
no because z^2 + 6= is not "The expression is not factorable with rational numbers."
Step-by-step explanation:
2. Which of the following is not an example of
a perfect square?
a. 9 +
b. 200
c. 4
.
d. 64
Answers
Answer:
B. 200
Step-by-step explanation:
A perfect square is the multiplication of two equal integers such as 1*1=1, 2*2=4, 3*3=9. From the examples, 1, 4, 9 are perfect square.
Non perfect square numbers are 1*2=2,
3*1=3,
5*1=5,
3*2=6,
6*1=6,
7*1=7
Examples of perfect squares:
1*1=1
2*2=4,
3*3=9,
4*4= 16,
5*5=25,
6*6=36,
7*7=49,
8*8=64,
9*9=81,
10*10=100,
11*11=121,
12*12=144,
13*13=169,
14*14=196,
15*15=225 and so on
SOLVE: 1/4 (20-4a)=6-a (show work please)
Answers
Answer:
a = 2
Step-by-step explanation:
1/4 (20-4a)=6-a
5 - 1 = 6 - a
4 = 6 - a
a = 6 - 4
a = 2
:) Hope this helps, please mark as brainliest!
need answer asp plss ty

Answers
Answer:
Step-by-step explanation:
U= {10,11,12,13,14,15,16,17,18,19,20}
a.
X=even numbers={10,12,14,16,18,20}
b.
Y=odd numbers={11,13,15,17,19}
c. draw a big circle call it U then
inside that big circle draw two small circles that do not touch or overlap
in one circle write the numbers in x , and on the other the numbers from y
What do you know about a quadratic equation that has the following points (2, 0) and (10, 0)?A. The parabola must open up.B. The parabola will have a negative y-intercept.C. The x-coordinate of the vertex must be 6.D. The graph must be wider than the parent function.
Answers
The equation of a parabola can be written in its factored form like this:
\(a(x-r_1)(x-r_2)\)Where a is a number known as the leading coeffcient and the r's are the roots or zeros of the function i.e. the x-values for which the function is equal to 0. At this x-values the parabola intercepts the x-axis so we know that it passes through the points:
\((r_1,0),(r_2,0)\)The leading coefficient a defines if the parabola opens up (a>0) or down (a<0) and if it's wider (|a|>1) or narrower (|a|<1) than the parent function x².
The question tells us that we only know that the parabola of the equation passes through (2,0) and (10,0). This implies that x=2 and x=10 are zeros of the parabola because the two points mentioned are in the x-axis. Then what we know about this equation is that is factored form looks like this:
\(a(x-2)(x-10)\)So "a" can take any value. Then we can't assure if the parabola opens up or down or if it's wider or narrower than the parent function so we can discard options A and D.
Now let's see what happens with the y-intercept. At the y-intercept the value of x is 0 so let's replace x with 0 in the factored form and see if the result is positive or negative:
\(a(0-2)(0-10)=a\cdot(-2)\cdot(-10)=20a\)But "a" can take any value which means that we don't know if the y-intercept is negative or positive so we can discard option B.
The x-coordinate of the vertex is the midvalue between the zeros. Since the zeros are x=2 and x=10 this midvalue is:
\(\frac{2+10}{2}=\frac{12}{2}=6\)So the x-coordinate of the vertex is 6.
AnswerSince options A, B and D are discarded and C was proved we have that the answer is option C.
how would I solve x^2 + 12x + 32 = 0 by completing the square?
Answers
Answer:
x = -4, -8
Step-by-step explanation:
Step 1: Write out quadratic
x² + 12x + 32 = 0
Step 2: Subtract 32 on both sides
x² + 12x = -32
Step 3: Complete the Square
x² + 12x + 36 = -32 + 36
(x + 6)² = 4
Step 4: Take square root of both sides
x + 6 = ±2
Step 5: Subtract 6 on both sides
x = -6 ± 2
x = -4, -8
The required solution of the given quadratic equation,x² + 12x + 32 = 0 is x = -4, or -8
Use the concept of quadratic equation defined as:
The definition of a quadratic as a second-degree polynomial equation demands that at least one squared term must be included. It also goes by the name quadratic equations. The quadratic equation has the following generic form:
ax² + bx + c = 0
The given quadratic equation is,
x² + 12x + 32 = 0
It can be written as,
x² + (2)(6)x + 32 = 0
For completing the square add 6² both sides,
x² + (2)(6)x + 6² + 32 = 6²
(x² + (2)(6)x + 6²) + 32 = 36
Subtracting 32 on both sides we get,
(x² + (2)(6)x + 6²) = 4
Since we know that the identity (a+b)² = a² + 2ab + b²
Therefore, the expression becomes,
(x+ 6)² = 4
Take square root on both sides,
x + 6 = ± 2
Subtract 6 on both sides,
x = -4, or -8
Hence,
The solution of the given quadratic equation is x = -4, or -8
To learn more about quadratic equations visit:
https://brainly.com/question/30098550
#SPJ6
The volume of the world's oceans is nearly 1.5⋅10^9 cubic kilometers. Write this number in scientific notation.
Answers
Answer:
"The World Ocean." The Columbia Encyclopedia. CD-ROM. 2007, 6th Ed. New York: Columbia University Press. "The World ocean has an area of about 361 million sq km (139,400,000 sq mi), an average depth of about 3,730 m (12,230)
Viau, Elizabeth Anne. World Builders: Water on Earth. California State University Los Angeles. 2003.
There are two origins of water: comets (extraterrestrial bombardment) and out gassing (condensation of steam from early volcanism). These processes are continuing today.
Step-by-step explanation:
(3x + 3x²) + (2x² + 2x)?
Answers
Answer:
=5x2+5x
Step-by-step explanation:
Let's simplify step-by-step.
3x+3x2+2x2+2x
Mr. Bell drove 440 miles in 8 hours, on the highway, at a steady speed. How far could he drive in five hours at the same average speed?
Answers
Answer: 250 miles
Step-by-step explanation: 440/8 = 50
50 x 5 = 250
Does anyone know the answer?

Answers
Answer:
33.7°
Step-by-step explanation:
the direction angle is calculated as
tanΘ = \(\frac{y}{x}\) ( Θ is the direction angle ) , then
tanΘ = \(\frac{-4}{-6}\) = \(\frac{2}{3}\)
Θ = \(tan^{-1}\) ( \(\frac{2}{3}\) ) ≈ 33.7° ( to the nearest tenth )
In a shipment of 65 vials, only 12 do not have hairline cracks. If you randomly select 2 vials from the shipment, what is the probability that all 2 of the selected vials have hairline cracks
Answers
The required probability is approximately 0.603 or 60.3%.
Given, In a shipment of 65 vials, only 12 do not have hairline cracks.
Therefore, number of vials having hairline cracks
= 65 - 12 = 53
We need to find the probability that all 2 of the selected vials have hairline cracks.
Here, both vials need to have hairline cracks.
Therefore, the probability can be found as follows:
Probability of selecting the first vial with a hairline crack = Number of vials with hairline crack / Total number of vials
= 53/65
Probability of selecting the second vial with a hairline crack,
given that the first vial had a hairline crack = Number of vials with hairline crack / Total number of remaining vials
= 52/64
Simplifying both the above expressions,
Probability of selecting 2 vials with hairline cracks
= (53/65) x (52/64)= 0.603
Approximately, the probability of selecting 2 vials with hairline cracks is 0.603 or 60.3%.
Hence, the required probability is approximately 0.603 or 60.3%.
To know more about probability visit:
https://brainly.com/question/32117953
#SPJ11
What is the slope of the line that passes through the points (-4, -4) and (6, 4)?
Answers
Answer:
8/10 or 4/5
Step-by-step explanation:
(n)The rise=8
(d)the run=10
8/10 or simplified is 4/5
Write the additive inverse of 3/2
Answers
Answer:
1.5
Step-by-step explanation:
2/2=1 so 2/1=0.5 so answer is 1.5
Answer:
- \(\frac{3}{2}\)
Step-by-step explanation:
The additive inverse is the value that requires to be added to make the sum zero, that is
\(\frac{3}{2}\) - \(\frac{3}{2}\) = 0
The additive inverse is - \(\frac{3}{2}\)
What is the image of the point (0,1) after a rotation of 270^ ∘ counterclockwise about the origin?
Answers
Answer:
it should be 1,1. nnhbnhh vfc thg there eventual
The image of the point (0,1) after a rotation of 270^ ∘ counterclockwise about the origin is (-1, 0).
How does rotation by 90 degrees changes the coordinates of a point if rotation is concerning origin?Let the point be having coordinates (x,y).
Case 1: If the point is in the first quadrant:
Subcase: Clockwise rotation:
Then (x,y) → (y, -x)
Subcase: Counterclockwise rotation:
Then (x,y) → (-y, x)
Case 2: If the point is in the second quadrant:
Subcase: Clockwise rotation:
Then (x,y) → (y, -x)
Subcase: Counterclockwise rotation:
Then (x,y) → (-y, x)
Case 3: If the point is in the third quadrant:
Subcase: Clockwise rotation:
Then (x,y) → (y, -x)
For points on axes, it can take that point in any of the two surrounding quadrants. Since if the point is on the positive x-axis, then it can take as of the first quadrant or fourth quadrant.
There is no effect as we assumed rotation is concerning origin.
(0,1) ---- (-1, 0)
Hence, the image of the point (0,1) after a rotation of 270^ ∘ counterclockwise about the origin is (-1, 0).
Learn more about the rotation of a point concerning origin here:
https://brainly.com/question/18856342
#SPJ2
The temperature was -5°F and then fell 8°F.
Which number line diagram could be used to represent this situation?
A number line diagram with an arrow that starts at 8, is 5 units long, and points to the left.
A number line diagram with an arrow that starts at 8, is 5 units long, and points to the right.
A number line diagram with an arrow that starts at -5, is 8 units long, and points to the left.
SA number line diagram with an arrow that starts at -5, is 8 units long, and points to the right.
Answers
Answer:
The diagram with an arrow that starts at -5, is 8 units long, and points to the left.
Step-by-step explanation:
Verify that the function y = 10 sin(4x) + 25 cos(4x) + 1 is a solution to the equation d²y/dx² +16y= 16.
Answers
The function y = 10 · sin 4x + 25 · cos 4x + 1 is a solution to differential equation d²y / dx² +16y= 16.
How to prove that an equation is a solution to a differential equation
Differential equations are expressions that involves functions and its derivatives, a function is a solution to a differential equation when an equivalence exists (i.e. 3 = 3).
In this question we need to prove that function y = 10 · sin 4x + 25 · cos 4x + 1 is a solution to d²y / dx² +16y= 16. First, find the first and second derivatives of the function:
dy / dx = 40 · cos 4x - 100 · sin 4x
dy² / dx² = - 160 · sin 4x - 400 · cos 4x
Second, substitute on the differential equation:
- 160 · sin 4x - 400 · cos 4x + 16 · (10 · sin 4x + 25 · cos 4x + 1) = 16
- 160 · sin 4x - 400 · cos 4x + 160 · sin 4x + 400 · cos 4x + 16 = 16
16 = 16
To learn more on differential equations: https://brainly.com/question/32538700
#SPJ4
Express 1/10 cm as a fraction of 3 metres
Answers
Answer:
1/3000
Step-by-step explanation:
3 meters to centimeters:
3 × 100 = 300
= 1/10 ÷ 300
= 1/10/300
= 1/(10×300)
= 1/3000
Brainliest question please help me please

Answers
Answer:
79.38 m^2
Step-by-step explanation:
Answer:
Step-by-step explanation:
TO=√((4²+(8+4)²)=√(16+144)=√160=√(16×10)=4√10
OU=√(2²+(4+2)²)=√(4+36)=√40=√(4×10)=2√10
area of triangle TOUR=lw=4√10×2√10=8×10=80 units²
Brett is performing a hypothesis test in which the population mean is 310 and the standard deviation is 20. His sample data has a mean of 295 and a sample size of 50. Which of the following correctly depicts the z-statistic for Brett’s data? –5. 30 –0. 11 4. 28 6. 27.
Answers
Z-score of given data comes to be -5.30.
It is given that
Population mean μ= 310
Standard deviation σ= 20
Mean of sample data X= 295
Sample size n= 50
What is z-score?A Z-score is a numerical measurement that describes a value's relationship to the mean of a group of values.
For a hypothesis test
Z-score = (X-μ)/(σ/√n)
Where, X = observed value
μ= mean
σ = standard deviation
n =sample size
Z-score of above data = (295-310)/(20/√50)
Z-score = -5.30
Therefore, Z-score of given data comes to be -5.30.
To get more about Z-score visit:
https://brainly.com/question/25638875
Write 4.36x10^-3 as an ordinary number
Answers
Answer: 0.00436
Step-by-step explanation:
Polynomial x²-6y²-xy-5x-5y+6 was factored into (x+ay+b)(x+cy-2) for constants a, b and c. Find the value of a+bc
Answers
Answer:
We know that the polynomial:
x²- 6y²- xy - 5x - 5y + 6
is rewritten as:
(x+ay+b)(x+cy-2)
First, lets expand the above expression:
x^2 + x*(cy) + x*(-2) + (ay)*x + (ay)*(cy) + (ay)*(-2) + b*x + b*(cy) - 2*b
Now we can simplify this to get:
x² + c*(xy) - 2*x + a*(xy) + ac*y² - 2a*y + b*x + bc*y - 2b
now let's group together the terms with the same variables:
x² + (c + a)*(xy) + (b - 2)*x + (bc - 2a)*y + ac*y² - 2b
And that must be equal to:
x²- 6y²- xy - 5x - 5y + 6
notice that equations are equal if and only if all the correspondent factors are equal.
notice that in both cases, the factor that multiplies the x² term is 1.
for the y² term we will have:
a*c = -6
for the xy term we will have
c + a = -1
for the x term we will have
b - 2 = - 5
for the y term we will have
bc - 2a = -5
for the constant term, we will have:
-2b = 6
Then we have a lot of equations, rewriting these we have:
a*c = -6
c + a = -1
b - 2 = -5
bc - 2a = -5
-2b = 6
From the fourth equation, b - 2 = -5
we can get:
b = -5 + 2 = -3
b = -3
notice that for the last equation:
-2b = 6
b = 6/-2 = -3
we have the same solution
Then we can replace the value of b in the above equations to get:
a*c = -6
c + a = -1
-3*c - 2a = -5
Now, we need to isolate one of the variables in one of the equations.
For example, we can isolate c in the second one to get:
c = -1 - a
now we can replace that in other equation, for example the third one:
-3*(-1 - a) - 2a = -5
now we can solve that for a.
3 + 3a - 2a = -5
3 + (3 - 2)a = -5
3 + a = -5
a = -5 - 3 = -8
a = -8
now we can use the equation "c = -1 - a" to find the value of c:
c = -1 -(-8) = -1 + 8 = 7
c = 7
then we have:
b = -3
a = -8
c = 7
then:
a + b*c = -8 + (-3)*7 = -8 - 21 = -29
T/F : There are exactly three vectors in span {a1,a2, a3}
Answers
False.
The number of vectors in the span of a set of vectors depends on the linear independence of the vectors.
The number of vectors in the span of a set of vectors depends on the linear independence of the vectors. If a set of vectors is linearly independent, then only the zero vector is in the span of the set. If a set of vectors is linearly dependent, then the span of the set contains infinitely many vectors.
So, the number of vectors in span {a1, a2, a3} can be 1, 2, or 3, depending on whether the set {a1, a2, a3} is linearly dependent or independent.
For example, if a1 = (1,0,0), a2 = (0,1,0), and a3 = (0,0,1), then {a1, a2, a3} is a linearly independent set, and the span of {a1, a2, a3} is just the set of all linear combinations of these vectors, which is the entire space R3. So, there are infinitely many vectors in the span of {a1, a2, a3}.
On the other hand, if a1 = (1,0,0), a2 = (2,0,0), and a3 = (0,1,0), then {a1, a2, a3} is a linearly dependent set, since a2 is a scalar multiple of a1. In this case, the span of {a1, a2, a3} is just the set of all linear combinations of a1 and a3, which is a plane in R3. So, there are infinitely many vectors in the span of {a1, a2, a3}.
Visit to know more about Vectors:-
brainly.com/question/25705666
#SPJ11
for conducting a two-tailed hypothesis test with a certain data set, using the smaller of n11 and n21 for the degrees of freedom results in df11, and the corresponding critical values are t2.201. using the formula for the exact degrees of freedom results in df19.063, and the corresponding critical values are t2.093. how is using the critical values of t2.201 more conservative than using the critical values of 2.093?
Answers
Using the critical values of t=+/-2.201 is less likely to lead to rejection of the null hypothesis than using the critical values of +/-2.093.
Critical Value Definition -
Critical value can be defined as a value that is compared to a test statistic in hypothesis testing to determine whether the null hypothesis is to be rejected or not.
If the value of the test statistic is less extreme than the critical value, then the null hypothesis cannot be rejected.
Critical values are essentially cut-off values that define regions where the test statistic is unlikely to lie; for example, a region where the critical value is exceeded with probability \alpha if the null hypothesis is true.
Using the critical values of t=±2.201 is more "conservative" than using the critical value of ±2.093 because it is more likely to reject the null hypothesis using the greater value i-e t=±2.201.
Learn more about Critical value
brainly.com/question/14508634
#SPJ4
Find the missing side lengths. Round all answers to the nearest tenth.

Answers
Answer:
81
Step-by-step explanation:
90+25= 115
115 - 34 = 81
Complete the table of values for f(x) = -3|x+1|-4 using the table of values for g(x) = |x|
Answers
f(x)>=-7
Functions:
Function, in mathematics, is an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable). Functions are ubiquitous in mathematics.
If a variable y is so related to a variable x that whenever a numerical value is assigned to x, there is a rule according to which a unique value of f(x)is determined, then f(x) is said to be a function of the independent variable x
Given :
f(x) = -3|x+1|-4
using the table of values for g(x) = |x|
Solution :
f(x) = -3|x+1|-4
f(x) = -3|g(x)+1|-4
f(x) = -3||x|+1|-4
which means |x| is always positive |x|>0
f(x) = -3||x|+1|-4
f(x) = -3x-3-4
f(x) = -3x-7
f(x)>=-7
For more details: brainly.com/question/18071485
#SPJ9
A number is called "bright" if it is 34 times larger than the sum of its digits. How many "bright" three-digit numbers are there?
A : 0
B : 1
C : 2
D : 3
E : 4
Answers
Step-by-step explanation:
Let the number be \(\overline{abc}=100a+10b+c\).
\(100a+10b+c=34a+34b+34c \\ \\ 66a-24b-33c=0 \\ \\ 22a-8b-11c=0\)
Taking the equation mod \(11\) yields \(-8b \equiv \pmod{11}\), meaning \(b=0\).
So, \(22a-11c=0 \implies c=2a\).
So, the only possibilites are \((a,c)=(1,2), (2,4),(3,6), (4,8)\).
Therefore, there are \(4\) such numbers.
How many 1/3 inch cubes does it take to fill a box with width 2 2/3 inches, lengths 3 1/3 inches, and height 2 1/3 inches?
Answers
Answer:
560 cubes
Step-by-step explanation:
width: 8 cubes
length: 10 cubes
height: 7 cubes
volume: 8*10*7=560
divided l, w, and h by 1/3 to get them in cubes
Answer:
Step-by-step explanation:
The awnser is multiply by 9 then multiply by 2
The restaurant in a large commercial building provides coffee for the occupants in the building. The restaurateur has determined that the mean number of cups of coffee consumed in a day by all the occupants is 2.0 with a standard deviation of .6. A new tenant of the building intends to have a total of 125 new mployees. What is the probability that the new employees will consume more than 240 cups per day?
Answers
To solve this problem, we can use the concept of the sampling distribution of the sample mean. The mean number of cups of coffee consumed in a day by all occupants is 2.0 with a standard deviation of 0.6. Since the sample size is large (125 employees) and the population standard deviation is known, we can approximate the sampling distribution of the sample mean as a normal distribution.
The mean of the sampling distribution is equal to the population mean, which is 2.0 cups per day Now, we need to calculate the z-score for the value of 240 cups per day using the formula:
z = (x - μ) / σ,
where x is the desired value (240 cups per day), μ is the mean of the sampling distribution (2.0 cups per day), and σ is the standard deviation of the sampling distribution (0.6 / sqrt(125)).
Plugging in the values, we have:
z = (240 - 2) / (0.6 / sqrt(125)) ≈ 58.01.
Finally, we can use a standard normal distribution table or a calculator to find the probability of obtaining a z-score greater than 58.01. However, since this z-score is extremely large, the probability will be very close to zero.
Learn more about standard deviation here: brainly.com/question/30390235
#SPJ11
Consider the differential equation: Y+ ay' + by = 0, where a and b are constant coefficients. Find the values of a and b for which the general solution of this equation is given by y(x) = cie -32 cos(2x) + c2e -3.2 sin(2x).
Answers
We have: a = -3, b = 2 Hence, the values of a and b for which the general solution of the differential equation is given by y(x) = c1e^(-3x^2)cos(2x) + c2e^(-3x^2)sin(2x) are a = -3 and b = 2.
To find the values of a and b for which the general solution of the differential equation y + ay' + by = 0 is given by y(x) = c1e^(-3x^2)cos(2x) + c2e^(-3x^2)sin(2x), we need to compare the general solution with the given solution and equate the coefficients.
Comparing the given solution with the general solution, we can observe that:
The term with the exponential function e^(-3x^2) is common to both solutions.
The coefficient of the cosine term in the given solution is ci, and the coefficient of the cosine term in the general solution is c1.
The coefficient of the sine term in the given solution is c2, and the coefficient of the sine term in the general solution is also c2.
From this comparison, we can deduce that the coefficient of the exponential term in the general solution must be 1.
Learn more more about general solution here:
https://brainly.com/question/32667290
#SPJ11
