Answers
The distance between the two points in the simplest radical form is √61
Distance between two pointsFrom the question, we are to determine the distance between the two marked points
The marked points are (-8, 6) and (-3, 0)
The distance, d, between two points can be calculated by using the formula,
d = √((x₂ - x₁)² + (y₂ - y₁)²)
x₁ = -8
x₂ = -3
y₁ = 6
y₂ = 0
Thus,
The distance, d, between the points is
d = √((-3 - -8)² + (0 - 6)²)
d = √((-3 + 8)² + ( -6)²)
d = √((5)² + 36)
d = √(25 + 36)
d = √61
Hence, the distance between the two points in the simplest radical form is √61
Learn more on Distance between two points here: https://brainly.com/question/17273444
#SPJ1
Related Questions
Find matrix M such that M × [3 -2 , 6 -8 ] = [-2 16]
Answers
The matrix M is: M = [2/9 -8/27 , 4/9 -8/27 ]
Let's say that M is a 2 x 2 matrix that satisfies M × [3 -2 , 6 -8 ] = [-2 16]. This means that the product of matrix M and matrix [3 -2 , 6 -8 ] will give us the result matrix [-2 16]. We know that the product of two matrices is equal to the sum of the products of their corresponding elements. We can use this knowledge to solve for the unknown elements in matrix M. Let us assume that M = [a b , c d] so that we can solve for its elements.
a(3) + b(6) = -2 ... (1) c(3) + d(6) = 16 ... (2) a(-2) + b(-8) = -2 ... (3) c(-2) + d(-8) = 16 ...
(4)Simplifying equations (1) to (4), we get:
3a + 6b = -2 ... (5) 3c + 6d = 16 ... (6) -2a - 8b = -2 ... (7) -2c - 8d = 16 ... (8)
Solving for a, b, c, and d, we get:a = 2/9 b = -8/27 c = 4/9 d = -8/27.
for such more questions on matrix
https://brainly.com/question/1279486
#SPJ8
The price of a pair of jeans originally are $50. Today they are on sale for
$30. What percent off (percent discount) are the pair of jeans?
Answers
Answer:
40% off
Step-by-step explanation:
50x2=100
30x2=60
100-60=40
40% off
Someone pls answer this with explanation

Answers
Answer:
EXPlaIN THIS TO ME cuz i have no idea
Step-by-step explanation:
Answer:
f(-1)=6
Step-by-step explanation:
Translate the graph to y=mx+b form
\(y=-2x+3\)
insert -1 for x and solve
y=-2(-1)+3
y=2+3
y=6
f(-1)=6
prove that 3 divides n3 + 2n whenever n is a positive integer.
Answers
Base case: When n = 1, we have 13 + 2(1) = 3, which is divisible by 3.
Inductive step: Assume that for some positive integer k, 3 divides k3 + 2k. We want to show that 3 divides (k+1)3 + 2(k+1).
Expanding the left side, we get:
(k+1)3 + 2(k+1) = k3 + 3k2 + 3k + 1 + 2k + 2
Simplifying, we get:
(k+1)3 + 2(k+1) = (k3 + 2k) + 3k2 + 3k + 3
By the inductive hypothesis, k3 + 2k is divisible by 3. Also, 3k2 + 3k is divisible by 3 because it has a common factor of 3. Therefore, (k+1)3 + 2(k+1) is divisible by 3.
Since the base case holds and the inductive step shows that if 3 divides k3 + 2k, then 3 divides (k+1)3 + 2(k+1), we can conclude that 3 divides n3 + 2n for any positive integer n.
A baby weighs 18 pounds at her four-month appointment. Six months later she weighs 24 pounds. By what percentage did the baby's weigh increase?
Answers
Answer:
75%
Step-by-step explanation:
18 / 24 = 0.75 (75%)
This is another way of saying the baby's weight increased by 75%.
Given the system of equations below. Use the Inverse of the matrix method to solve. x+2y+3z=11
2x+4y+5z=21
3x+5y+6z=27
Answers
The solution of the given system of equations is x = -4, y = 5 and z = 2 is the answer.
The system of equations given below:x + 2y + 3z = 11;2x + 4y + 5z = 21;3x + 5y + 6z = 27.
Here, we will solve this system of equations using inverse of the matrix method as follows:
We can write the given system of equations in matrix form as AX = B where, A = [1 2 3; 2 4 5; 3 5 6], X = [x; y; z] and B = [11; 21; 27].
The inverse of matrix A is given by the formula: A-1 = (1/ det(A)) [d11 d12 d13; d21 d22 d23; d31 d32 d33] where,
d11 = A22A33 – A23A32 = (4 × 6) – (5 × 5) = -1,
d12 = -(A21A33 – A23A31) = -[ (2 × 6) – (5 × 3)] = 3,
d13 = A21A32 – A22A31 = (2 × 5) – (4 × 3) = -2,
d21 = -(A12A33 – A13A32) = -[(2 × 6) – (5 × 3)] = 3,
d22 = A11A33 – A13A31 = (1 × 6) – (3 × 3) = 0,
d23 = -(A11A32 – A12A31) = -[(1 × 5) – (2 × 3)] = 1,
d31 = A12A23 – A13A22 = (2 × 5) – (3 × 4) = -2,
d32 = -(A11A23 – A13A21) = -[(1 × 5) – (3 × 3)] = 4,
d33 = A11A22 – A12A21 = (1 × 4) – (2 × 2) = 0.
We have A-1 = (-1/1) [0 3 -2; 3 0 1; -2 1 0] = [0 -3 2; -3 0 -1; 2 -1 0]
Now, X = A-1 B = [0 -3 2; -3 0 -1; 2 -1 0] [11; 21; 27] = [-4; 5; 2]
Therefore, the solution of the given system of equations is x = -4, y = 5 and z = 2.
know more about matrix method
https://brainly.com/question/32106604
#SPJ11
In triangle XYZ, m2Y = 63.25° and mzZ= 28.8°. Determine the measure of the exterior angle to X.
O92.05°
87.95°
061.20⁰
26.75°
ASAP!!
Answers
The value of the exterior angle of the measure of the angle X is found as 120.85°.
Explain the term linear pair?When two lines cross at one point, a linear pair with angles is created. If the angles follow the intersections of the two lines in a straight line, they are referred to as linear. A linear pair's total angles are always proportional to 180°.For the stated question-
Three angles of the triangle XYZ are-
∠Y = 63.25°
∠Z = 28.8°.
then, by angle sum property of triangle.
∠X + ∠Y + ∠Z = 180
∠X = 180 - 63.25° - 28.8°.
∠X = 87.95
Thus, exterior angle to X.
Exterior angle = 180 - ∠X (linear pair)
Exterior angle = 180 - 87.95
Exterior angle = 120.85°
Thus, the value of the exterior angle of the measure of the angle X is found as 120.85°.
To know more about the linear pair, here
https://brainly.com/question/18944511
#SPJ1
Answer:
the answer is 87.95
Step-by-step explanation:
the body mass of a man is xkg.thebody mass of his two children are five-sixth and four_fifths of their father5 x over 6 + 4 x over 5 5 x over 6 + 4 x over 5
Answers
56/120
Step-by-step explanation:
The body masses of the two children in terms of their father's body mass, x, are:
First child's body mass = 5x/6 kg
Second child's body mass = 4x/5 kg
To express the body mass of the man's two children in terms of their father's body mass, we can use the given ratios.
Let the body mass of the man be x kg.
The first child's body mass is five-sixths of their father's body mass:
Body mass of the first child = (5/6) * x
= 5x/6 kg.
The second child's body mass is four-fifths of their father's body mass:
Body mass of the second child = (4/5) * x
= 4x/5 kg.
Therefore, the body masses of the two children in terms of their father's body mass, x, are:
First child's body mass = 5x/6 kg
Second child's body mass = 4x/5 kg
Learn more about the ratio here:
brainly.com/question/1504221
#SPJ4
1/10 + 6 2/5 + 5 3/4 This is A Math Problem.
Answers
Answer: 12 1/4 or 49/4
Step-by-step explanation:
And you’re welcome
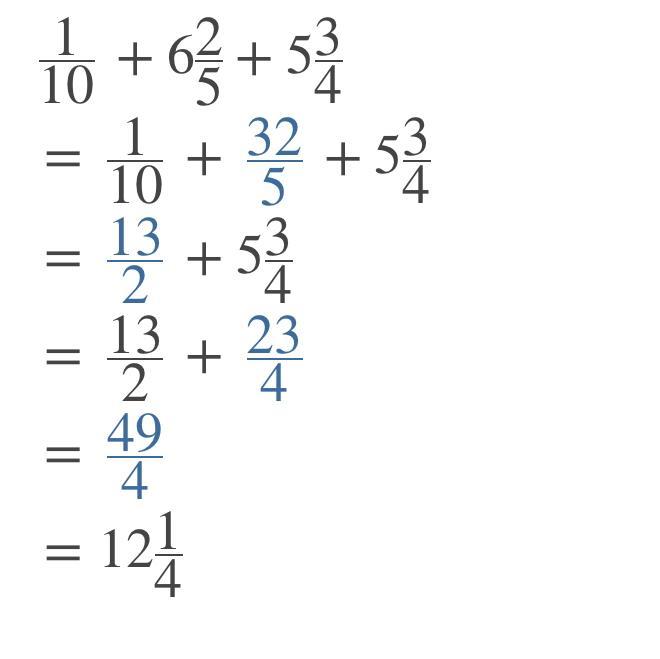
what does the highest point on a bell-shaped curve represent?
Answers
The highest point on a bell-shaped curve represents the peak or maximum value of the distribution. This point is known as the mode of the distribution.
In a bell-shaped curve, also known as a normal distribution or Gaussian distribution, the data is symmetrically distributed around the mean. The curve is characterized by a central peak, and the highest point on this peak corresponds to the mode.
The mode represents the most frequently occurring value or the value that has the highest frequency in the dataset. It is the point of highest density in the distribution.
The bell-shaped curve is often used to model naturally occurring phenomena and is widely applied in statistics and probability theory. The mode provides information about the most common or typical value in the dataset and is useful for understanding the central tendency of the distribution.
While the mean and median also have significance in a normal distribution, the highest point on the bell-shaped curve specifically represents the mode, indicating the value with the highest occurrence in the dataset.
Learn more about Gaussian distribution at: brainly.com/question/29734279
#SPJ11
Construct a confidence interval for p1-p2 at the given level of confidence.
x1=30, n1=235, x2=39, n2=294, 90 % confidence
Answers
Using the z-distribution, the 90% confidence interval for the difference of proportions is given by: (-0.0534, 0.0434).
What is the mean and the standard error for the distribution of differences?For each sample, the mean and the standard error are given as follows:
\(p_1 = \frac{30}{235} = 0.1277, s_1 = \sqrt{\frac{0.1277(0.8723)}{235}} = 0.0218\).\(p_2 = \frac{39}{294} = 0.1327, s_1 = \sqrt{\frac{0.1327(0.8673)}{294}} = 0.0198\).For the distribution of differences, they are given by:
\(\overline{p} = p_1 - p_2 = 0.1277 - 0.1327 = -0.005\).\(s = \sqrt{s_1^2 + s_2^2} = \sqrt{0.0218^2 + 0.0198^2} = 0.0294\)What is the confidence interval?The interval is given by:
\(\overline{p} \pm zs\)
In this problem, we have a 90% confidence level, hence\(\alpha = 0.9\), z is the value of Z that has a p-value of \(\frac{1+0.9}{2} = 0.95\), so the critical value is z = 1.645.
Hence the bounds of the interval are:
\(\overline{p} - zs = -0.005 - 1.645(0.0294) = -0.0534\)
\(\overline{p} + zs = -0.005 + 1.645(0.0294) = 0.0434\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
how to know if a function has a vertical asymptote
Answers
To determine if a function has a vertical asymptote, you need to consider its behavior as the input approaches certain values.
A vertical asymptote occurs when the function approaches positive or negative infinity as the input approaches a specific value. Here's how you can determine if a function has a vertical asymptote:
Check for restrictions in the domain: Look for values of the input variable where the function is undefined or has a division by zero. These can indicate potential vertical asymptotes.
Evaluate the limit as the input approaches the suspected values: Calculate the limit of the function as the input approaches the suspected values from both sides (approaching from the left and right). If the limit approaches positive or negative infinity, a vertical asymptote exists at that value.
For example, if a rational function has a denominator that becomes zero at a certain value, such as x = 2, evaluate the limits of the function as x approaches 2 from the left and right. If the limits are positive or negative infinity, then there is a vertical asymptote at x = 2.
In summary, to determine if a function has a vertical asymptote, check for restrictions in the domain and evaluate the limits as the input approaches suspected values. If the limits approach positive or negative infinity, there is a vertical asymptote at that value.
know more about vertical asymptote.
https://brainly.com/question/29260395
#SPJ11
Which tatement would be the mot important in explaining why 2 3 = 6 9 ? A quare i hown and divided into 9 equal-ized quare of 3 row and 3 column. The firt two column are haded. A. 6 of the 9 ame-ized quare are haded and therefore repreent 2 3. B. 6 of the 9 ame-ized quare are haded and therefore repreent 6 9. C. The haded area repreent both 2 3 and 6 9 of the whole hape. D. 2 of the 3 column are haded and therefore repreent 6 9
Answers
The most appropriate statement is that C. The shaded area represent both 2/3 and 6/9 of the whole shape.
What are Fractions?Fractions are numbers which are of the form a/b where a and b are real numbers. This implies that a parts of a number b.
Given a square.
This square is divided in to 9 equal sized squares, with 3 rows and 3 columns.
Out of the 9 equal sized squares, 6 squares are shaded.
We can write the fraction of shaded squares to total number of squares as 6/9.
In the same way, we have in the question that, 6 squares which are shaded is the squares in the first two columns, where each column has three squares.
So we can say that, out of 3 equal sized columns, two columns are shaded.
Fraction of shaded columns to total columns is 2/3.
So 2/3 = 6/9.
Hence shaded area represent both 2/3 and 6/9 of the whole shape.
Learn more about Fractions here :
https://brainly.com/question/10354322
#SPJ1

What is the slope of the following graph? Plzz help <3

Answers
Answer:
-2/5
Step-by-step explanation:
The solution comes rom the formula for finding the slope of a graph: Rise/Run
In this case, the rise would be -2, because it is going down the graph 2 points. The run would be 5, because it is going to the right 5 points. Hopefully this will help you in the future.
first to answer correctly gets brainleist! (bringing out a lot of questions so yea!)

Answers
Answer:
C.
Step-by-step explanation:
The easiest way to tell if a relation is a function is to look at the values of the x's. If more than one x is the same, it cannot be a function. In contrast, if more than one y is the same, it is okay. The answers A, B, and D are functions because the x's are all different. Looking at the table for the answer C, you can see that two x's are the same (there are two x's with the value of 1).
Hope this helps!! Have a wonderful day :D
Lisa bought a treadmill for $925. She made a 20% down payment and financed the rest over 18 months. Find the monthly payment if the interest rate was 11%.
Answers
The monthly payment if the interest rate was 11% will be $45.63.
The remaining amount is calculated as,
P = (1 - 0.20) x $925
P = 0.80 x $925
P = $740
The monthly payment is calculated as,
MP = [$740 + ($740 x 0.11)] / 18
MP = $821.4 / 18
MP = $45.63
More about the monthly payment link is given below.
https://brainly.com/question/14064255
#SPJ1
The monthly payment is $49.69.
We have,
The amount of the down payment is:
0.20 x $925 = $185
So the amount financed is:
$925 - $185 = $740
Using the formula for the monthly payment on a loan:
= (Pr(1+r)^n) / ((1+r)^n - 1)
where:
P = principal or amount financed = $740
r = monthly interest rate = 11%/12 = 0.0091667
n = total number of payments = 18
Plugging in the values, we get:
Monthly payment
= ($7400.0091667 x (1+0.0091667)^18) / ((1 + 0.0091667)^18 - 1)
= $49.69 (rounded to the nearest cent)
Therefore,
The monthly payment is $49.69.
Learn more about monthly payments here:
https://brainly.com/question/30664343
#SPJ1
the power to which a number or expression is raised
Answers
The power to which a number or expression is raised is called the exponent.
1. An exponent is a mathematical notation that represents the power to which a number or expression is raised. It is written as a superscript number or variable placed above and to the right of the base number or expression.
2. The base number or expression is the number or expression that is being multiplied repeatedly by itself, raised to the power of the exponent.
3. The exponent tells us how many times the base number or expression should be multiplied by itself. For example, in the expression \(2^3\), the base is 2 and the exponent is 3. This means that 2 should be multiplied by itself three times: 2 * 2 * 2 = 8.
4. The exponent can be a positive whole number, a negative number, zero, or a fraction. Each of these cases has different interpretations:
- Positive exponent: Indicates repeated multiplication. For example, \(2^4\)means 2 multiplied by itself four times.
- Negative exponent: Indicates the reciprocal of the base raised to the positive exponent. For example, \(2^{-3\) means 1 divided by \(2^3\).
- Zero exponent: Always equals 1. For example, \(2^0\) = 1.
- Fractional exponent: Represents a root. For example, \(4^{(1/2)\)represents the square root of 4.
5. Exponents follow certain mathematical properties, such as the product rule \((a^m * a^n = a^{(m+n)})\), the quotient rule \((a^m / a^n = a^{(m-n)})\), and the power rule \(((a^m)^n = a^{(m*n)})\).
Remember to use these rules and definitions to correctly interpret and evaluate expressions involving exponents.
For more such questions on exponent, click on:
https://brainly.com/question/11975096
#SPJ8
A sales manager for an advertising agency believes there is a relationship between the number of contacts that a salesperson makes and the amount of sales dollars earned. A regression ANOVA shows the following results. ANOVA df SS MS F Significance F Regression 1.00 13,591.17 13,591.17 156.38 0.00 Residual 8.00 657.95 86.68 Total 9.00 14,249.12 What is the value of the coefficient of determination?
Multiple Choice
−0.9538
0.9766
0.6344
0.9538
Answers
The coefficient of determination, denoted by R^2, is a measure of how well the regression model fits the data. It represents the proportion of the total variation in the dependent variable (sales dollars) that is explained by the independent variable (number of contacts).
In this case, we can use the formula:
R^2 = SS_regression / SS_total
where SS_regression is the sum of squares of the regression (13,591.17) and SS_total is the total sum of squares (14,249.12).
Thus,
R^2 = 13,591.17 / 14,249.12
R^2 = 0.953
Therefore, the coefficient of determination is 0.953 or 95.3%. This means that 95.3% of the variation in sales dollars can be explained by the number of contacts made by the salesperson, and the remaining 4.7% is due to other factors not included in the model.
To know more about coefficient of determination visit:
https://brainly.com/question/28975079
#SPJ11
Write the equation of the line in slope-intercept form that passes through the points (5,3) and (1,−5).
Answers
Answer:
y = −2x + 8
Step-by-step explanation:
y = −2x + 8, the answer is this because, in order to find the slope, you must use the formula y2-y1/x2-x1, and the y-intercept is found by using the formula y=mx+b, in which b is the y-intercept which leads to the awnser, y = −2x + 8.
Hi! Your answer is y = −2x + 8
Step-by-step explanation:
In order to find the slope, you have to use y2-y1/x2-x1 for the formula. The y-intercept can be found by using the formula y=mx+b. This means b is the y-intercept which makes the answer: y = −2x + 8.
Hope this helps! Have a good day :)
HELP!!!!
Help me please !!!!

Answers
Answer:
I think the answer is C but i'm not an expert with this so sorry if you get it wrong :(
Step-by-step explanation:
Answer:
I think is c but I'm not really sure
y= -3x-2
6x+2y= -4
What is the solution to this problem?
Answers
1 Substitute y=-3x-2y=−3x−2 into 6x+2y=-46x+2y=−4.
-4=-4−4=−4
2 Since -4=-4−4=−4 is redundant information, this is a dependent system.
Infinitely Many Solutions
Given: y varies directly with x and has a constant rate of change of 7. when the value of y is 12, then the value of x would be _____.
Answers
Answer:X=12/7
Step-by-step explanation:
Y \(\alpha\) X
⇒Y=KX
Where K is the constant
From the question,k=7
⇒ When Y=12,
y=KX
12=7X
X=12/7
Find x, y, and z. Please Show work how you did!

Answers
Answer:
y=36,x=108,z=30
Step-by-step explanation:
1)180°=72°+(3y)°
=>(3y)°=180°-72°
=>(3y)°=108°
=>3y=108
=>y=36
2)(x)°=(3y)°=>x=108
3)(3z+18)°=108°=>3z+18=108=>3z=90=>z=30
Answer:
x = 108
y = 36
z = 30
Step-by-step explanation:
(x)° + 72° = 180° (interior angles on the same side of transversal)
-> (x)° = 180 - 72°
-> (x)° = 108°
-> x = 108
(3y)° = (x)° (corresponding angles)
-> 3y = x
-> 3y = 108
-> y = 108/3
-> y = 36
(3z + 18)° = (x)° (corresponding angles)
-> 3z + 18 = x
-> 3z + 18 = 108 - 18
-> 3z = 108 - 18
-> 3z = 90
-> z = 90/3
-> z = 30
10. A line has equation y=3kx−2k and a curve has equation y=x 2
−kx+2, where k is a constant. a) Find the set of values of k for which the line and curve meet at two distinet points. b) For cach of two particular values of k, the line is a tangent to the curve. Show that these two tangents meet on the x-axis. 11. The equation x 2
+px+q=0, where p and q are constants, has roots −3 and 5 . a) Find the values of p and q. b) Using these values of p and q, find the value of the constant r for which the equation x 2
+px+q+r=0 has equal roots. 12. A curve has equation y=x 2
−4x+4 and a line has the equation y=mx, where m is a constant. a) For the case where m=1, the curve and the line intersect at the point A and B. b) Find the coordinates of the mid-point of AB. c) Find the non-zero value of m for which the line is the tangent to the curve, and find the coordinates of the point where the tangent touches the curve. Answer: 1. ( 2
1
,0) 9. a) 25−(x−5) 2
2. a) (3x− 2
5
) 2
− 4
25
b) (5,25) b) − 3
1
3
10. a) k>1,k<− 2
1
Answers
a) The set of values of k for which the line and curve meet at two distinct points is k < -2/5 or k > 2.
To find the set of values of k for which the line and curve meet at two distinct points, we need to solve the equation:
x^2 - kx + 2 = 3kx - 2k
Rearranging, we get:
x^2 - (3k + k)x + 2k + 2 = 0
For the line and curve to meet at two distinct points, this equation must have two distinct real roots. This means that the discriminant of the quadratic equation must be greater than zero:
(3k + k)^2 - 4(2k + 2) > 0
Simplifying, we get:
5k^2 - 8k - 8 > 0
Using the quadratic formula, we can find the roots of this inequality:
\(k < (-(-8) - \sqrt{((-8)^2 - 4(5)(-8)))} / (2(5)) = -2/5\\ or\\ k > (-(-8)) + \sqrt{((-8)^2 - 4(5)(-8)))} / (2(5)) = 2\)
Therefore, the set of values of k for which the line and curve meet at two distinct points is k < -2/5 or k > 2.
b) To find the two values of k for which the line is a tangent to the curve, we need to find the values of k for which the line is parallel to the tangent to the curve at the point of intersection. For m to be the slope of the tangent at the point of intersection, we need to have:
2x - 4 = m
3k = m
Substituting the first equation into the second, we get:
3k = 2x - 4
Solving for x, we get:
x = (3/2)k + (2/3)
Substituting this value of x into the equation of the curve, we get:
y = ((3/2)k + (2/3))^2 - k((3/2)k + (2/3)) + 2
Simplifying, we get:
y = (9/4)k^2 + (8/9) - (5/3)k
For this equation to have a double root, the discriminant must be zero:
(-5/3)^2 - 4(9/4)(8/9) = 0
Simplifying, we get:
25/9 - 8/3 = 0
Therefore, the constant term is 8/3. Solving for k, we get:
(9/4)k^2 - (5/3)k + 8/3 = 0
Using the quadratic formula, we get:
\(k = (-(-5/3) ± \sqrt{((-5/3)^2 - 4(9/4)(8/3)))} / (2(9/4)) = -1/3 \\or \\k= 4/3\)
Therefore, the two values of k for which the line is a tangent to the curve are k = -1/3 and k = 4/3. To show that the two tangents meet on the x-axis, we can find the x-coordinate of the point of intersection:
For k = -1/3, the x-coordinate is x = (3/2)(-1/3) + (2/3) = 1
For k = 4/3, the x-coordinate is x = (3/2)(4/3) + (2/3) = 3
Therefore, the two tangents meet on the x-axis at x = 2.
Learn more about " line and curve" : https://brainly.com/question/30162650
#SPJ11
Point slope form question
How would I turn (2,-5) (-3, 10) into a point slope equation?
Answers
Answer:
y+5=-3(x-2)
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(10-(-5))/(-3-2)
m=(10+5)/-5
m=15/-5
m=-3
y-y1=m(x-x1)
y-(-5)=-3(x-2)
y+5=-3(x-2)
Which expression has a value of 24?
PLS HELP ASAP
A –6 • 2 – (–7)–6 • 2 – (–7)
B 9 • 4 ÷ 2 + (–3)9 • 4 ÷ 2 + (–3)
C –9 + 3 – 6 • (–5)–9 + 3 – 6 • (–5)
D 9 ÷ 3 • 10 – (–1) + 3
Answers
Answer:
a) the answer it 10 so no
b) the answer is −39 so nah
c) the answer is 48, nope
d) the answer is 34, did you mean to write 34 instead of 24?
Step-by-step explanation:
1.12 as a mixed number ?
Answers
Answer:
1 12/100
Step-by-step explanation:
Answer:
Yes
Step-by-step explanation:
It can converted to 28/25 or 1 and 3/25
Write an equation of a line
passing through the point
(-6, -3) and perpendicular to JK
with J(-2, -7) and K(6, 5).
A) y = -2/3x – 4 the airport
B) y = -2/3x – 7 the library
C) y = 2/3x + 1 the park
D) y = 2/3x + 9 the zoo
E) y = -3/2x – 4 the police station
Answers
The equation of the line passing through the point (-6, -3) and perpendicular to JK with J(-2, -7) and K(6, 5) is y = -2 / 3x - 7, so option B is correct.
What is line?
An object having an endless length and no width, depth, or curvature is called a line. Since lines can exist in two, three, or higher-dimensional environments, they are one-dimensional things.
Given:
A line passing through the point (-6, -3) and perpendicular to JK with J(-2, -7) and K(6, 5)
Calculate the slope of the line,
m = 5 - (-7) / 6 - (-)
m = 12 / 8
m = 3 / 2
The slope of a line perpendicular to JK, M = - 1 / 3 / 2 = -2 / 3
Calculate the equation of the line as shown below,
y - (-3) = -2 / 3[x - (-6)]
y + 3 = -2 / 3x - 4
y = -2 / 3x - 7
Therefore, the equation of the line passing through the point (-6, -3) and perpendicular to JK with J(-2, -7) and K(6, 5) is y = -2 / 3x - 7.
To know more about the line:
https://brainly.com/question/2696693
#SPJ1
The sum of the elements in a tuple can be recursively calculated as follows: the sum of the elements in a tuple of size 0 is 0 otherwise, the sum is the value of the first element added to the sum of the rest of the elements write a function named sum that accepts a tuple as an argument and returns the sum of the elements in the tuple.
Answers
The following is a code in python.
What is Python and why it is used?Python is a popular computer programming language used to create software and websites, automate processes, and analyze data. Python is a general-purpose language, which means it can be used to make many different types of programs and isn't tailored for any particular issues.
What are the advantages of Python?One of Python's biggest benefits is the variety of libraries and frameworks it offers. Everything from data visualization, machine learning, data science, natural language processing, and complex data analysis uses the Python Library, from NumPy to TensorFlow.
#Specify the function in
DefinedSum(tu)
# Verify whether the tuple contains 0
if len(tu) == 0
#Then, give back 0
return 0
#Otherwise
else:
#invoke the recursive function.
return tu[0]+Sum (tu[1:])
Set a variable of the tuple type
tu=(2,5,1,8,10)
#print, then invoke the function.
print("The total of tuple is:"), sum(tu),
Output:
The sum of tuple is: 26
Here, we define the method "sum()" and send the parameter "tu" to the function, which saves the value of the tuple type.
If the length of the tuple is 0, then the if conditional expression should verify the condition and return 0.
If not, invoke the function, return the tuple's total (which is determined recursively), and exit.
Last but not least, initialize the "tu" variable of the tuple type, print, then run the sum function.
To learn more about python, click the following link :-
https://brainly.com/question/14239610
#SPJ1
answers for number 21 and 24 questions

Answers
22. f(x)=4.5
23. f(x)=1/4x+7/4 or f(x)=1/4x+1.75 or f(x)=1/4x+1 3/4. (Depends on how your teacher wants the y intercept written)
24. f(x)=-3/2x-7/2 or f(x)=-3/2x-3.5 or f(x)=-3/2x-3 1/2
