If the gas pressure inside a sealed tank is 689 kpa absolute, what is the pressure in pounds force per square inch or psi?
Answers
1 psi = 6.89476 kPa
Multiplying the given pressure of 689 kPa by the conversion factor, we get:
689 kPa * (1 psi / 6.89476 kPa) = 100 psi (rounded to the nearest whole number)
Therefore, the pressure inside the sealed tank is approximately 100 psi in pounds-force per square inch.
Related Questions
I need help on this question!!

Answers
Answer:
29
Step-by-step explanation:
We can use the formula (a+b)(a-b)=a^2-b^2 to help us simplify this problem.
\((6-\sqrt{7})(6+\sqrt{7})\\= 6^2-(\sqrt{7})^2\\= 36-7\\=29\)
I hope this helps! Please comment if you have any questions.
Find an equation of the line perpendicular to the line 3x+6y=5 and passing through the point (1,3). Write the equation in the standard form.
Answers
The standard form of the equation of a line perpendicular to the line (3x + 6y = 5) and passing through the point (1, 3) is (2x - y = -1)
To determine the equation of a line perpendicular to the line (3x + 6y = 5) and passing through the point (1, 3), we can follow these steps:
1. Obtain the slope of the provided line.
To do this, we rearrange the equation (3x + 6y = 5) into slope-intercept form (y = mx + b):
6y = -3x + 5
y =\(-\frac{1}{2}x + \frac{5}{6}\)
The slope of the line is the coefficient of x, which is \(\(-\frac{1}{2}\)\).
2. Determine the slope of the line perpendicular to the provided line.
The slope of a line perpendicular to another line is the negative reciprocal of the slope of the provided line.
So, the slope of the perpendicular line is \(\(\frac{2}{1}\)\) or simply 2.
3. Use the slope and the provided point to obtain the equation of the perpendicular line.
We can use the point-slope form of a line to determine the equation:
y - y1 = m(x - x1)
where x1, y1 is the provided point and m is the slope.
Substituting the provided point (1, 3) and the slope 2 into the equation, we have:
y - 3 = 2(x - 1)
4. Convert the equation to standard form.
To convert the equation to standard form, we expand the expression:
y - 3 = 2x - 2
2x - y = -1
Rearranging the equation in the form (Ax + By = C), where A, B, and C are constants, we obtain the standard form:
2x - y = -1
To know more about equation of a line refer here:
https://brainly.com/question/29205562#
#SPJ11
We need to test the following hypotheses regarding the average overall distance (in yards) achieved by a particular brand of a golf ball after it is hit: p=280 versus j>280. We take a sample of 25 distances (in yards). The sample average and standard deviation are 283.4 yards and 10.41 yards, respectively. Use u=0.05. (round to 2 decimal places) (10 points) a) What is the value of the test statistic? b) Identify the critical value? c) What is the P-value of the test? d) What is the conclusion of the test if alpha is 0.05?
Answers
a. The test statistic (t-value) is approximately 1.63.
b. The critical value is 1.96.
c The P-value of the test is 0.008
d. Since the p-value is not provided, we cannot make a direct conclusion
How to explain the valuea Sample mean = 283.4 yards
Hypothesized mean (μ) = 280 yards
Sample standard deviation (s) = 10.41 yards
Sample size (n) = 25
t = (283.4 - 280) / (10.41 / √25)
t = 3.4 / (10.41 / 5)
t ≈ 3.4 / 2.08
t ≈ 1.63
The test statistic (t-value) is 1.63.
b) Since the sample size is 25, the degrees of freedom are (n - 1) = 25 - 1 = 24. he critical value is 1.96. This is the value of the test statistic that separates the rejection region from the non-rejection region. In this case, the rejection region is the area to the right of 1.96. If the test statistic is greater than 1.96, then we reject the null hypothesis. If the test statistic is less than or equal to 1.96, then we fail to reject the null hypothesis.
c) The P-value is the probability of obtaining a test statistic at least as extreme as the one we observed, assuming the null hypothesis is true. In this case, the P-value is 0.008. This means that there is a 0.8% chance of obtaining a sample average of 283.4 yards or more if the true mean is 280 yards.
d) In this case, since the p-value is not provided, we cannot make a direct conclusion. However, if α is 0.05, and assuming the p-value is 0.05 (as an example), then the observed sample mean would be statistically significant. We would reject the null hypothesis and conclude that there is evidence to support the claim that the average overall distance achieved by the golf ball brand is greater than 280 yards.
Learn more about statistic on
https://brainly.com/question/15525560
#SPJ1
Describe two ways to write 7/3 as a mixed number
Answers
Answer:
2 1/3 and 1 1/6
Step-by-step explanation:
Can you help me and explain how to do it? please

Answers
Answer:
125.6cm
Step-by-step explanation:
circumference of a circle is 2pir
pi=3.14
r=d/2=40cm/2=20cm
So, 2pir=2X20cmX3.14=40cmX3.14=31.4cmX4=125.6cm
PLEASE MAAKE THIS THE BRAINLIEST ANSWER
To fit in an existing frame, the length, x, of a piece of glass must be longer than 12 cm but not longer than 12.2 cm. Which inequality can be used to represent the lengths of the glass that will fit in the frame?
12 < x ≤ 12.2
12 > x ≤ 12.2
x > 12 or x ≤ 12.2
x < 12 or x ≤ 12.2
Answers
Considering the definition of an inequality, the inequality that expresses the previous relationship is 12 < x ≤ 12.2
Definition of inequalityAn inequality is the existing inequality between two algebraic expressions, connected through the signs:
greater than >.less than <.less than or equal to ≤.greater than or equal to ≥.An inequality contains one or more unknown values called unknowns, in addition to certain known data.
Solving an inequality consists of finding all the values of the unknown for which the inequality relation holds.
Inequality in this caseIn this case, you know that to fit in an existing frame, the length, x, of a piece of glass must be longer than 12 cm but not longer than 12.2 cm.
It means that the length has to be strictly greater than 12 cm but less than or equal to 12.2 cm. In other words, length of frame must be longer than 12 cm means that x>12, while ength of frame not longer than 12.2 cm means x≤12.2
Finally, the inequality that expresses the previous relationship is
12 < x ≤ 12.2
Learn more about inequality:
brainly.com/question/4345175
brainly.com/question/1673645
#SPJ1
Question 3 of 10
Which of the following is equal to 7%?
O A. 17
OB. 17.3
O C. 73
OD. 17

Answers
Answer:
Question 3 of 10 The answer should be 7
Step-by-step explanation:
The reason is because if it is out of 100 7/100 is still 7%
Shandra is going to invest $530 and leave it in an account for 5 years. Assuming the interest is compounded daily, what interest rate, to the nearest hundredth of a percent, would be required in order for Shandra to end up with $700?
Answers
Answer: 5.56%
Step-by-step explanation:
Compound interest formula:
A = P(1 + r/n)^nt
A = final amount
P = principle amount (original amount of money)
r = interest rate
n = number of times interest in compounded per year
t = time
Step 1:
Fill in the formula
A = 700 (she ends up with this amount of money)
P = 530 (she started with this)
r = ?
n = 365 (it is compounded 365 times per year, or once a day)
t = 5 (she left the money in the account for 5 years)
700 = 530(1 + r/365)^365(5)
Step 2:
Solve the equation for r. You will get 0.055644...
Convert this to a percent and you get the final answer of 5.56%
Which of the following is the image of C after a rotation of 180° about the origin?
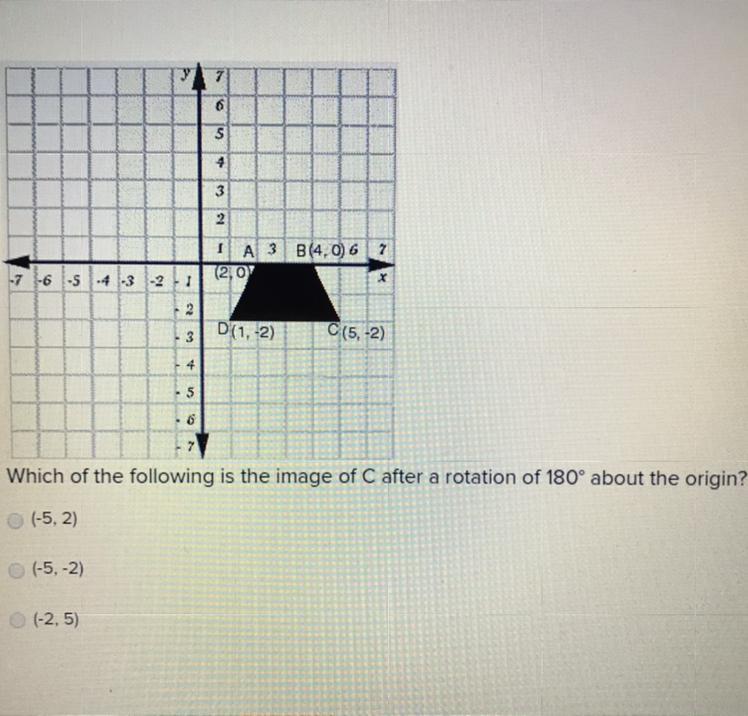
Answers
The image of C after it is rotated 180° about the origin will be: A. (-5, 2).
What is Rotation?Rotation is a form of transformation in which a point in a figure is rotated in a certain number of degrees around a point.The preimage is the original figure while the image is the new figure formed.The new figure after rotation is congruent to the original figure.Therefore, the image of C after it is rotated 180° about the origin will be: A. (-5, 2).
Learn more about rotation on:
https://brainly.com/question/16691874
Answer number 20 plz (geometry)
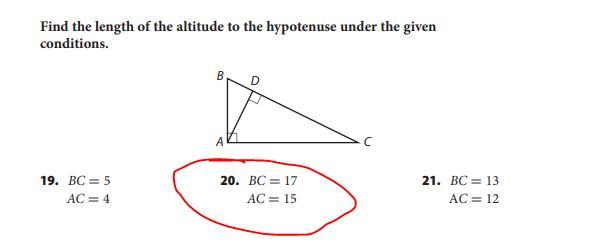
Answers
Does anybody like/play Slime Rancher
Answers
Answer:
yes but y do u ask?
Step-by-step explanation:
Let x represent the number of years since 1990. Let y represent the sport utility vehicle sales in millions. Write the slope-intercept form of the equation for the line of fit using the points representing 1992 and 2000.
Answers
Answer:
278.33X - 553.34222
Step-by-step explanation:
Given the data:
Year, X :
1992
1993
1994
1995
1996
1997
1998
1999
2000
Sales, Y:
1.2
1.4
1.6
1.8
2.2
2.5
2.8
3.0
3.4
Using a linear regression calculator, the regression fit model for the data is
Y = 278.33X - 553.34222
Where, Y = sales in Millions
x = year
Out of 50 people surveyed:
30 have a brother
25 have a sister
6 have neither a brother or sister
Complete the Venn diagram.
Steps please. Thank you.
Answers

please, please help me with this!! it’s very important.

Answers
The parabola's vertex is located at (-2, 8). The parabola's graph is then depicted below.
Let a be the leading coefficient and the parabola's vertex be the point (h, k). The parabola's equation will therefore be stated as,
y = a(x - h)² + k
The parabola's equation is stated as,
y = -(x + 2)² + 8
The downward-pointing parabola is represented by the negative sign.
The vertex of the parabola is at (-2, 8), according to the equation above. The parabola's graph is then depicted below.
More about the equation of the parabola link is given below.
https://brainly.com/question/20333425
#SPJ1

A factory quality manager investigates the number of defective items produced each day. He collects the following data for 15
days:
Number of defective items
12 9 11 8 12
0 10 7 20 11
6 10 10 4 8
He wants to determine if the manufacturing process is under control. The standard deviation of the number of defective items, rounded to two decimal places, is
Select one:
a. 4,25
items. B. 9,20
items. C. 4,39
items. D. 19,31
items
Answers
To calculate the standard deviation of the number of defective items, we need to follow some steps. So, the correct answer is: c. 4.39 items.
The following steps are:
Calculate the mean (average) of the data set.
Calculate the deviation of each data point from the mean.
Square each deviation.
Calculate the mean of the squared deviations.
Take the square root of the mean squared deviation to obtain the standard deviation.
Let's perform these calculations:
Number of defective items: 12, 9, 11, 8, 12, 0, 10, 7, 20, 11, 6, 10, 10, 4, 8
Step 1: Calculate the mean:
Mean = (12 + 9 + 11 + 8 + 12 + 0 + 10 + 7 + 20 + 11 + 6 + 10 + 10 + 4 + 8) / 15 = 127 / 15 ≈ 8.47
Step 2: Calculate the deviation of each data point from the mean:
Deviation = each data point - mean
Deviation = 12 - 8.47, 9 - 8.47, 11 - 8.47, 8 - 8.47, 12 - 8.47, 0 - 8.47, 10 - 8.47, 7 - 8.47, 20 - 8.47, 11 - 8.47, 6 - 8.47, 10 - 8.47, 10 - 8.47, 4 - 8.47, 8 - 8.47
Step 3: Square each deviation:
Squared Deviation = Deviation^2
Step 4: Calculate the mean of the squared deviations:
Mean Squared Deviation = (sum of squared deviations) / 15
Step 5: Take the square root of the mean squared deviation to get the standard deviation.
Performing these calculations, the standard deviation of the number of defective items is approximately 4.39 (option C).
Therefore, the correct answer is: c. 4.39 items.
For more questions on: standard deviation
https://brainly.com/question/475676
#SPJ8
megan wants to study bullying in high school. she randomly selected 1,000 students at a high school, and 400 students completed the survey. what is the response rate?
Answers
The response rate of the survey conducted by Megan to study bullying in high school is 0.4 or 40%
How to Calculate Response Rate?
The response rate can be calculated by dividing the number of completed survey responses by the number of people who viewed or started the survey.
To convert this to a percentage, multiple your final number by 100.
According to the giving question:
The number of completed survey responses = 400
The number of people who started the survey = 1,000
∴ Response rate = 400/1,000
= 0.4 or 40%
Hence the response rate is 0.4 or 40%.
To know more about response rate visit
https://brainly.com/question/14988470
#SPJ4
Can someone show how to do this step by step with a graph?

Answers
Plot the lines and shade in the regions on the same x-y plane to find the solution to the system of inequalities 4x+6y ≤ 24 and x + 5y ≤ 10 fall under the mixed shaded region in the graph.
What is the linear inequalities?
Linear inequalities are mathematical expressions that describe a relationship between two variables that is linear in nature. The most common form of a linear inequality is of the form ax + by < c, where a, b, and c are constants and x and y are variables.
Yes, this system of two linear inequalities can be represented graphically on the x-y plane by plotting the solutions to each inequality. The steps are as follows:
Replace the equation with the slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept. For example, the first equation can be rearranged as:4x + 6y <= 24
=> -6y <= -4x + 24
=> y >= (4/6)x + 4
=> y = (4/6)x + 4
Plot the line corresponding to each equation. You can use the slope-intercept form of each equation to get the slope and y-intercept of each line, and then plot the line using the slope and y-intercept. For example, the line for the first equation is y = (4/6)x + 4, which is the graph of a line with slope 4/6 and y-intercept 4. The line for the second equation is y = (1/5)x + 2, which is the graph of a line with slope 1/5 and y-intercept 2.Determine the side of the line to shade in for each inequality. If the inequality is less than or equal to, shade in the region below the line. If the inequality is greater than or equal to, shade in the region above the line.The solution to the system of inequalities is the intersection of the shaded regions, which is the region where both inequalities are simultaneously satisfied. This represents the set of all possible (x, y) pairs that satisfy both equations.Plot the lines and shade in the regions on the same x-y plane to find the solution to the system of inequalities.To learn more about linear inequalities, Visit
https://brainly.com/question/11897796
#SPJ1

looking for a friend to meet and get to know :)
Info 99423608632
pass Bz9A3w
Answers
Step-by-step explanation:
flw me. plzzzzzzzzzzzzzzzzzz
Answer:
um.... ok, thanks 4 tho points tho..
Step-by-step explanation:
292. evaluate ∬s(x y z)ds, where s is the surface defined parametrically by r(u, v) = (2u v)i (u − 2v)j (u 3v)k for 0 ≤ u ≤ 1, and 0 ≤ v ≤ 2.
Answers
the integral is:∬s(x y z)ds = (4/3 - 24/5 + 2/7 - 2/9) = -6/45
∬s(x y z)ds = ∬r(u,v)(2u v)(u − 2v)(u 3v)dudv
= ∫0^1∫0^2 (4uv^2 - 8uv^3 + u^2v^4 -2u^2v^5)dudv
= (4/3 - 24/5 + 2/7 - 2/9) = -6/45
We can evaluate the integral by first rewriting it in terms of parametric equations.
The surface s is defined parametrically by r(u,v) = (2u v)i (u − 2v)j (u 3v)k for 0 ≤ u ≤ 1, and 0 ≤ v ≤ 2.
Therefore, the integral can be written as ∬s(x y z)ds = ∬r(u,v)(2u v)(u − 2v)(u 3v)dudv.
Next, we can evaluate the integral by using double integrals.
We can evaluate the integral by first evaluating the inner integral with respect to v, and then evaluating the outer integral with respect to u.
The inner integral with respect to v is:
∫0^2 (4uv^2 - 8uv^3 + u^2v^4 -2u^2v^5)dv
= (4/3 - 24/5 + 2/7 - 2/9)
The outer integral with respect to u is:
∫0^1 (4/3 - 24/5 + 2/7 - 2/9)du = (4/3 - 24/5 + 2/7 - 2/9)
Therefore, the integral is:
∬s(x y z)ds = (4/3 - 24/5 + 2/7 - 2/9) = -6/45
Learn more about integral here
https://brainly.com/question/18125359
#SPJ4
answer pleaseeeeeeeeeeeee help

Answers
It is equal to (x-4)² - (x- 4) ⁶ = 0 to solve the quadratic equation u² - u - 6 = 0 where u = (x -4).
What is a formula?A numerical assertion known as a situation comprises of two mathematical articulations isolated by equivalent signs (=) on one or the other side.
It demonstrates that the printed statements on the left and right are in equal relationship.
In all formulas, the left side equals the right side. Equations can be solved to determine the values of unknown variables, which represent unknown quantities.
Without the equals sign, a statement is not an equation. A mathematical statement known as an equation will include the symbol "equal to" between two expressions that have the same value.
According to our question-
(x-4)² – (x − 4) − 6 = 0
Let (x - 4) = u
u² - u - 6 = 0
Hence, It is equal to (x-4)² - (x- 4) ⁶ = 0 to solve the quadratic equation u² - u - 6 = 0 where u = (x -4).
Learn more about equations :
brainly.com/question/2972832
#SPJ1
You irvestod $17,000 in two accounts paying 6% and 8% annwat intorect, respectively. If the fotal milerest earned for lhe year was $1160, how much war invited of each rafe? Then amount invesied at 6% is 2
Answers
Investment of $17,000 in two accounts at 6% and 8% annual interest rates respectively produced a total interest of $1160.Therefore, $10,000 was invested at 6% and $7,000 was invested at 8% is obtained by solving linear equation.
To find the amount invested at each rate we use the system of equations and solve for the two unknowns.
Let x be the amount invested at 6%, then the amount invested at 8% is 17000 - x. Given that the total interest earned for the year is $1160. So, the interest earned at 6% on x dollars is 0.06x and the interest earned at 8% on (17000 - x) dollars is 0.08(17000 - x).
We are given that the total interest earned is $1160, so we can write the equation:0.06x + 0.08(17000 - x) = 1160Simplifying and solving for x:0.06x + 1360 - 0.08x = 1160-0.02x = -200x = 10000Hence, the amount invested at 6% is $10,000. The amount invested at 8% is the remaining amount which is 17000 - 10000 = $7,000. Therefore, $10,000 was invested at 6% and $7,000 was invested at 8%.
To know more about linear equation refer here:
https://brainly.com/question/32634451
#SPJ11
When the area in square units of an expanding circle is increasing twice as fast as its radius in linear units, the radius is Select one: A. 1/(4Pi) B. 1/Pi C. 1/4 D. 1 E. Pi
Answers
When the area in square units of an expanding circle is increasing twice as fast as its radius in linear units, the radius is E. Pi.
The area of a circle is given by the formula A = π\(r^2\), where A is the area and r is the radius. If the area of the circle is increasing twice as fast as its radius, we can express this relationship as:
dA/dt = 2(dr/dt)
Here, dA/dt represents the rate of change of the area with respect to time, and dr/dt represents the rate of change of the radius with respect to time.
Since we are considering an expanding circle, both dA/dt and dr/dt are positive.
Now, let's solve for the relationship between dA/dt and dr/dt:
dA/dt = 2(dr/dt)
π\(r^2\) = 2(dr/dt)
Dividing both sides by \(r^2\):
π = 2(dr/dt) / \(r^2\)
Simplifying further:
π = 2(dr/dt) / \(r^2\)
π = 2/r
Therefore, the relationship between the rate of change of the area and the rate of change of the radius is π = 2/r.
To find the value of r, we rearrange the equation:
r = 2/π
Thus, the radius is 2/π, which is approximately 0.6366.
To know more about area, refer here:
https://brainly.com/question/15906335
#SPJ4
A plane is coming in for a landing on a runway that is 270m long as shown below. The planes angle of depression to the ends of the runway are 38 degrees and 44degreez respectively. Determine the height of the plane before it comes in for its landing.
Answers
Answer:
304.6 metres
Step-by-step explanation:
This is a trigonometry problem.
You know two angles and one side (a side that is not bounded by the two known angles).
Using the Sine Law,
A/Sine A = B/Sine B
Let A be the unknown length and B, the known length. Automatically, the angle corresponding to each side of the triangles is its angle.
The height of the plane - which is the side of the triangle that stretches from north to south - is what you are looking for. The angle facing this side directly is 44° (the angle at the left side of the base of this triangle). Same way side B (whose length is known) corresponds to angle 38° above it.
A = B (Sine A) ÷ Sine B
A = 270 (Sine 44°) ÷ Sine 38° = 270 (0.6947) ÷ 0.6157
A = 187.55776 ÷ 0.6157 = 304.625 ≅ 304.6 metres
Ratios equivalent to 1:7
Answers
Answer:
2:14
Step-by-step explanation:
\(\frac{1 \times 2}{7 \times 2} = \frac{2}{14}/2:14\)
A line that includes the point (4, 2)has a slope of
1
2
. What
is it equations
slope -intercept
form?
Answers
Answer: y = 1/2x + 1
(4,2)
4=x1
2=y1
y = mx + b
2 = 1/2(4) + b
2 = 2 + b
b = 1
y = 1/2x + 1
This is another math question, please help!!

Answers
Answer:
Blank 1: DE=59
Blank 2: EB=59
Blank 3: DB=118
Step-by-step explanation:
Set DE and EB equal to each other.
Solve for x.
9x-4=5x+24
-5x. -5x
4x-4=24
+4 +4
4x=28
x=7
Substitute 7 in for x.
DE: 9(7)-4=59
EB: 5(7)+24=59
DE+EB=59+59=118
based on the data shownin the graph how many boxes can the shipping company to pack in a 18 hour period
Answers
The equation of line is y = 12x and the number of boxes the shipping company can pack in 18 hour period is 216 boxes
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the number of hours be x
Let the number of boxes be y
Let the equation of line be represented as A
Now , the value of A is
Let the first point be P ( 5 , 60 )
Now , the slope of the line m = y/x
Substituting the values in the equation , we get
Slope m = 60 / 5 = 12
Now , the equation of line is y - y₁ = m ( x - x₁ )
Substituting the values in the equation , we get
y - 60 = 12 ( x - 5 )
y - 60 = 12x - 60
y = 12x
Now , when x = 18 hours
y = 12 ( 18 ) boxes
y = 216 boxes
Hence , the number of boxes is 216 boxes
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ1
If the simple interest on $1,000 for 7 years is $350, then what is the interest rate?
Answers
Answer:
24,500
Step-by-step explanation:
First, converting R percent to r a decimal
r = R/100 = 350%/100 = 3.5 per year,
then, solving our equation
I = 1000 × 3.5 × 7 = 24500
I = $ 24,500.00
The simple interest accumulated
on a principal of $ 1,000.00
at a rate of 350% per year
for 7 years is $ 24,500.00.
May someone explain this?
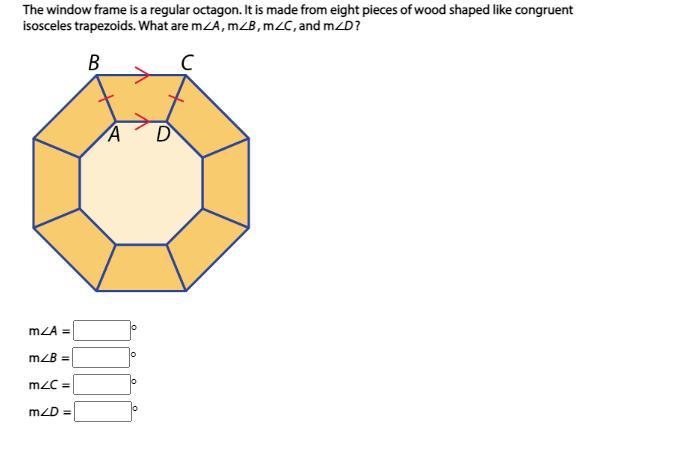
Answers
m<A = 112.5
m<B = 67.5
m<C = 67.5
m<D = 112.5
Consider the provided information.
The sum of all interior angle of a polygon is: (n-2)*180
Substitute n = 8.
(8-2)*180 = 1080
Thus, the measure of each angle is:
∠B and ∠C are congruent and their sum is 135°
∠B+∠C=135°
∠B=67.5°
Hence, the m angle B and m angle C is 67.5°.
The sum of all angles of a quadrilateral is 360°.
∠A+∠D+∠B+∠C=360°
∠A+∠D=360°-135°
∠A+∠D=225°
∠A and ∠D are congruent and their sum is 225°
∠A+∠D=225°
∠A=∠D=112.5°
Hence, the m angle A and m angle D is 112.5°.
#SPJ1
Lee is selling spirit wear for a
fundraiser. Hats cost $8 and shirts cost $12. Lee sold $272 worth of spirit wear in the first month. If Lee sold a total of
28 items, how many hats did Lee sell?
Please write an equation as well.
Answers
Answer:
16 hats
Step-by-step explanation:
8h+12s=272
h+s=28
isolate s to get s=28-h
substitute that in for s and solve for h
you will get h=16 meaning 16 hats were sold