In the figure BD||EG and the measure of angleACB=35 degree. What is the measure of angle GFH
A 35. B 55. C 135. D 145

Answers
Answer:
35 degree
Step-by-step explanation:
same degree as GFH
Related Questions
Lucy's dog lost 6 pounds. How much weight does her dog have to gain in order to have a net change of 0 pounds?
Answers
Lucy's dog needs to gain 6 pounds.
Lucy's dog lost 6 pounds so the dog will have to gain 6 pounds.
A bird is attempting to fly northeast at a constant speed, but a wind blowing southward at 5 miles per
hour blows the bird off course. If the bird’s overall movement (incorporating its intended movement
and the movement due to wind) is at a speed of √53 miles per hour, how fast would it have been traveling if there was no wind?
Answers
Answer:
The value is \(v_b = 9.89 \ miles /hour\)
Step-by-step explanation:
From the question we are told that
The velocity of the wind southward is \(v = 5 j \ miles / hour\)
The resultant velocity of the bird with the with wind is \(V= \sqrt{53}\)
Generally for an object moving in the northwest direction the angle with the horizontal is 45°
Generally the velocity of the bird in the along the x -axis is
\(V_x= v_b cos 45^o i\)
Generally the velocity of the bird in the along the y -axis is
\( V_y=(v_b sin 45^o - 5)j\)
Here \(v_b\) is the velocity of the bird without the wind
Generally the resultant velocity of the bird with the with wind is mathematically represented as
\(V = \sqrt{V_x^2 + V_y^2 }\)
=> \( \sqrt{53} = \sqrt{(v_b cos 45^o)^2 + (v_b sin 45^o - 5)^2 }\)
Generally
\(sin 45^o = \frac{1}{\sqrt{2} }\)
and
\(cos 45^o = \frac{1}{\sqrt{2} }\)
So
\( \sqrt{53} = \sqrt{(v_b* (\frac{1}{\sqrt{2} ))^2 + ([v_b * (\frac{1}{\sqrt{2} ) ]- 5)^2 }\)
=> \(53 = \frac{1}{2} v_b^2 + \frac{1}{2} v_b^2 + 5^2 -2*5 * \frac{1}{\sqrt{2} } v_b\)
=> \( 53 = v_b^2 + 25 - 5 \sqrt{2} v_b\)
=> \( v_b^2 - 5 \sqrt{2} v_b -28 = 0\)
Solving the above quadratic equation using quadratic formula we obtain that
\(v_b = 9.89 \ miles /hour\)
The other value is negative so we do not make use of it because we know that the bird is moving in the positive x and y axis
Solve |y-2|<10
please
Answers
Y=(-8, 12)

Wouldnt the answer be anything above 12? Because if Y is unknown, and you're taking 2 away from it, and it still has to be greater than 10, then it should be anything above 12. Unless it's saying that the number is greater than 10, and you are just taking away 2 from a number and it doesn't have to be greater than 10.
Write the symbols for the probability that of all the outfielders, a player is not a great hitter.
Answers
The symbolic representation of the conditional probability
\(P(G'|O) = \frac{P(G'nO)}{P(O)}\)
This is a conditional probability problem ; which can be expressed explicitly as ;
The probability of not being a great hitter Given that the player is an outfielder Recall :Probability of A given B is defined as ;
\(P(A|B) = \frac{P(AnB)}{P(B)} \)
Let :
Probability that a player is an outfielders = P(O)
Probability that a player is a Great hitter = P(G)
Probability that a player is not a great hitter = P(G') Probability that a player is not a great hitter given that he is an outfielder = P(OnG')Therefore, we have :
\(P(G'|O) = \frac{P(G'nO)}{P(O)}\)
Learn more : https://brainly.com/question/18153040
Dinah went out to eat at a restaurant. She wants to leave the waitress a tip of 18%. She can determine the amount she should pay by adding the total amount of the bill (b) to 18% of b + 18% ×b. Which expression shows another way that dinah can calculate the total amount she will pay, Including tip? Help me plssss

Answers
Answer:
C. \(1.18b\)
Step-by-step explanation:
Hi! Ace here!
In order to do this, we have to convert 18% into a decimal.
The decimal form of it is .18.
So we have to do
\(b+.18b\)
Combine like terms:
\(1.18b\)
I hope this helped
Answer:
1.18b
Step-by-step explanation:
Remember: percentage = decimal × 100
total = b + 18% x b
Factor out b:
total = b x (1 + 18%) = b x (1 + 0.18)
total = b x 1.18 = 1.18b
complete this item. (enter letter variables in alphabetical order.) rewrite the expression so that it has no denominator.
Answers
The given expression is $\frac{6}{t}+\frac{8}{u}-\frac{9}{v}$ and we need to rewrite this expression without any denominator in it. Step-by-step explanation: We can use the concept of the Least Common Multiple (LCM) of the denominators to remove the fractions in the expression. By taking the LCM of the denominators of the given expression, we have,$LCM\text{ of }t, u, v = t \cdot u \cdot v$ Now, multiplying each term of the given expression with the LCM $t \cdot u \cdot v$, we get,$\frac{6}{t}\cdot t \cdot u \cdot v+\frac{8}{u}\cdot t \cdot u \cdot v-\frac{9}{v}\cdot t \cdot u \cdot v$$6uv + 8tv - 9tu$$\therefore \text{The given expression without any denominator is } 6uv + 8tv - 9tu.$Thus, we can rewrite the given expression $\frac{6}{t}+\frac{8}{u}-\frac{9}{v}$ without any denominator in it as $6uv + 8tv - 9tu$.
LCM (a,b) in mathematics stands for the least common multiple, or LCM, of two numbers, such as a and b. The smallest or least positive integer that is divisible by both a and b is known as the LCM. Take the positive integers 4 and 6 as an illustration.
There are four multiples: 4,8,12,16,20,24.
6, 12, 18, and 24 are multiples of 6.
12, 24, 36, 48, and so on are frequent multiples for the numbers 4 and 6. In that lot, 12 would be the least frequent number. Now let's attempt to get the LCM of 24 and 15.
LCM of 24 and 15 is equal to 222235 = 120.
Know more about LCM here:
https://brainly.com/question/24510622
#SPJ11
Let pi = P{X = i} and suppose that p1 + p2 + p3 = 1. If E[X] = 2, what values of p1, p2, p3 (a) maximize and (b) minimize Var(X)?
Answers
The values of p1, p2, p3 that minimize Var(X) are p1 = 0, p2 = 1/3, and p3 = 2/3.
We can use the following formulas to find the variance of X:
Var(X) = E[X^2] - (E[X])^2
E[X] = p1 + 2p2 + 3p3
E[X^2] = p1 + 4p2 + 9p3
Substituting these expressions into the formula for the variance, we get:
Var(X) = p1 + 4p2 + 9p3 - (p1 + 2p2 + 3p3)^2
Simplifying this expression, we get:
Var(X) = -\((p1^2 + 2p2^2 + 3p3^2) + 2p1p2 + 6p1p3 + 4p2p3\)
To maximize Var(X), we want to maximize this expression subject to the constraint p1 + p2 + p3 = 1. We can use Lagrange multipliers to find the maximum. Let:
L(p1, p2, p3, λ) = -\((p1^2 + 2p2^2 + 3p3^2) + 2p1p2 + 6p1p3 + 4p2p3 + λ(1 - p1 - p2 - p3)\)
Taking partial derivatives and setting them equal to zero, we get:
-2p1 + 2p2 + 6p3 - λ = 0
4p1 - 4p2 + 4p3 - λ = 0
6p1 + 8p2 - 6p3 - λ = 0
p1 + p2 + p3 = 1
Solving these equations, we get:
p1 = 2/7, p2 = 3/7, p3 = 2/7, λ = 4/7
Therefore, the values of p1, p2, p3 that maximize Var(X) are p1 = 2/7, p2 = 3/7, and p3 = 2/7.
To minimize Var(X), we want to minimize the expression \(-(p1^2 + 2p2^2 + 3p3^2) + 2p1p2 + 6p1p3 + 4p2p3\) subject to the constraint p1 + p2 + p3 = 1. We can use the same Lagrange multiplier method to find the minimum. Taking partial derivatives and setting them equal to zero, we get:
-2p1 + 2p2 + 6p3 - λ = 0
4p1 - 4p2 + 4p3 - λ = 0
6p1 + 8p2 - 6p3 - λ = 0
p1 + p2 + p3 = 1
Solving these equations, we get:
p1 = 0, p2 = 1/3, p3 = 2/3, λ = 2/3
Therefore, the values of p1, p2, p3 that minimize Var(X) are p1 = 0, p2 = 1/3, and p3 = 2/3.
Learn more about expressions
https://brainly.com/question/14083225
#SPJ4
Hey guys help me with this question plzzzzzz

Answers
Answer:
625 cm³ and 64000 cm³
Step-by-step explanation:
Given
x = \(\sqrt[3]{V}\) ( cube both sides )
x³ = V
(a)
x = 25 cm , then
V = 25³ = 625 cm³
(b)
x = 40 cm , then
V = 40³ = 64 000 cm³
Given the box plot, will the mean or the median provide a better description of the center?
A. The mean, because the data distribution is symmetrical
B. The mean, because the data distribution is skewed to the left
C. The median, because the data distribution is skewed to the left
D. The median, because the data distribution is skewed to the right

Answers
a small town in the UK has only 600 high school students. what is the largest possible sample you can take from this town and still be able to calculate the standard deviation of the sampling distribution of p-hat?
Answers
To calculate the standard deviation of the sampling distribution of p-hat, the answer will be 59 students.
By calculating,
600/10=60 and 59 students which is less than 10% of the population.
A sampling distribution, also known as a finite-sample distribution, in statistics is the probability distribution of a given random-sample-based statistic. The sampling distribution is the probability distribution of the values that the statistic takes on if an arbitrarily large number of samples, each involving multiple observations (data points), were used separately to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample. Although only one sample is frequently observed, the theoretical sampling distribution can be determined.
Because they offer a significant simplification before drawing conclusions using statistics, sampling distributions are crucial in the field. They enable analytical decisions to be made based on the probability distribution of a statistic rather than the combined probability distribution of all the individual sample values
To learn more about standard deviation: https://brainly.com/question/475676
#SPJ4
y
12
11
10
9
7
NWO0065
4
-12-11-10-9-8
-65
-3-2-1
1
2 3 4 5 6
8 9 10 11 12
-2
-9
-10
-11
-12

Answers
Answer:
y12111097
Step-by-step explanation:
because I know the answer
x+2y=8
-x+3y=17
método de reducción ¿alguien la sabe?
Answers
Answer:
x=-2
y=5
Step-by-step explanation:
x+2y=8 equation-1
-x+3y=17 equation-2
5y=25
Both side divided 5,
y=5
Equation-1, y=5
x+2(5)=8
x+10=8
Both side -10
x+10-10=8-10
x=-2
Equation-2, y=5
-x+3(5)=17
-x+15=17
Both side -15
-x+15-15=17-15
-x=2
x=-2
Find two numbers if their lcm is 120 and hcf is 4
Answers
Answer:
HCF × LCM = product of two numbers
product = 120 × 4 = 480
possible pairs of number
(4,120),(8,60),(12,40),(20,24)
can you begin solving x-2/x+3 ≥2 by multiplying both sides of the inequality by x+3? Explain your answer.
Answers
Answer:
yes, but there is a better way
Step-by-step explanation:
instead of multiplying x+3 on both sides, I would instead subtract 2 on both sides. If you do this, it would be easier to write this equation in standard form and find the intervals.
In summary, to solve the inequality (x - 2)/(x + 3) ≥ 2, we can multiply both sides of the inequality by x + 3 only when x > -3 to preserve the direction of the inequality.
To solve the inequality (x - 2)/(x + 3) ≥ 2, we need to consider the impact of multiplying both sides of the inequality by x + 3.
When multiplying both sides of an inequality by a positive number, the direction of the inequality remains the same. However, if we multiply both sides by a negative number, the direction of the inequality is reversed.
In this case, the expression x + 3 is in the denominator of the left side of the inequality. If we multiply both sides of the inequality by x + 3, we need to consider two scenarios:
If x + 3 is positive: In this case, we can multiply both sides of the inequality by x + 3 without changing the direction of the inequality.
If x + 3 is negative: Multiplying both sides of the inequality by x + 3 would require flipping the direction of the inequality.
Therefore, we need to ensure that x + 3 is positive before multiplying both sides by x + 3 to preserve the direction of the inequality.
To determine when x + 3 is positive, we set the denominator equal to zero and solve for x:
x + 3 = 0
x = -3
So, if x > -3, then x + 3 is positive.
In summary, to solve the inequality (x - 2)/(x + 3) ≥ 2, we can multiply both sides of the inequality by x + 3 only when x > -3 to preserve the direction of the inequality.
To know more about "inequality." here
https://brainly.com/question/25944814
#SPJ2
two angles that add up to 90 degrees are called ________ angles.
Answers
two angles that add up to 90 degrees are called complementary angles.
The Skateboard club has 2 different colors of skateboards blue and red. Can you find the number of skateboards of each color, if the total number of skateboards is 15, and their product is 44?
Answers
Answer:
The number of skateboards of each color is 11 and 4
Step-by-step explanation:
Let x represent blue skateboards and
y represent red skateboards.
From the question, the total number of skateboards is 15, that is,
x + y = 15 ...... (1)
and their product is 44, that is,
xy = 44 ...... (2)
From equation (1),
x + y = 15
We can write that
x = 15 - y ...... (3)
Substitute this into equation (2)
xy = 44
(15-y)y = 44
15y -y² = 44
Then,
y² - 15y + 44 = 0
Solve quadratically
y² -4y -11y + 44 = 0
y(y-4) -11(y-4) = 0
(y-11)(y-4) = 0
y-11 = 0 OR y-4 = 0
y = 11 OR y = 4
Put the values of y into equation (3) for x
x = 15 - y
When y = 11
x = 15 - 11
x = 4
and when y = 4
x = 15 -4
x = 11
(4,11) and (11,4)
It is either 4 blue and 11 red skateboards OR 11 blue and 4 red skateboards.
Hence, the number of skateboards of each color is 11 and 4.
The edge town eagle football team is having a tough season. During one game, they lost a total of 62 yards in 8 plays. What is the average ball movement per play?
Answers
Two vertices of a right triangle have coordinates (5, 12) and (11, 12). The segment that connects these points is a leg of the triangle.
Which coordinate pair for the third vertex would create a right triangle?
Responses
(19, 12)
, left parenthesis 19 comma 12 right parenthesis,
(8, 20)
, left parenthesis 8 comma 20 right parenthesis,
(8, 12)
, left parenthesis 8 comma 12 right parenthesis,
(11, 4)
, left parenthesis 11 comma 4 right parenthesis,
Answers
The answer is (A) (11, 4).
Step-by-step explanation: Given that two vertices of a right-angled triangle are A(5, 12) and B(11, 12).
We can plot the given points on the co-ordinate plane as shown in the attached figure.
We will then see that only the point C(11, 4) will lie exactly below the point B(11, 12). Also, the segment AB and BC are the legs of the triangle, AC is the hypotenuse.
The lengths of the three sides are
\(AB = 11 - 5 = 6\\\\BC = 12 - 4 = 8\\\\AC = \sqrt{AB^{2} +BC^{2} } = \sqrt{6x^{2}+8^{2} } = \sqrt{100} = 10\)
Thus, the correct option is (A).
The Gallup Poll asked a random sample of 1785 adults if they attended church during the past week. Let p
∧
be the proportion of people in the sample who attended church. A newspaper report claims that 40% of all U.S. adults went to church last week. Suppose this claim is true. a. Verify the conditions for a valid sampling distribution for p : b. Describe the sampling distribution of p : c. Of the poll respondents, 44% said they did attend church last week. Find the probability of obtaining a sample of 1785 adults in which 44% or more say they attended church last week, assuming the newspaper report's claim is true.
Answers
a. The conditions for a valid sampling distribution for p are:
Randomization Condition: The sample of 1785 adults must be selected randomly from the population of all U.S. adults.
10% Condition: The sample size, 1785, must be less than 10% of the population of all U.S. adults.
Success/Failure Condition: The number of successes (people who attended church) and failures (people who did not attend church) in the sample must both be at least 10.
b. The sampling distribution of p is approximately normal with mean equal to the true proportion of U.S. adults who attended church last week, which is given as 0.40 in the newspaper report. The standard deviation of the sampling distribution can be calculated using the formula:
sqrt[(p*(1-p))/n]
where p is the true proportion and n is the sample size. Substituting p=0.40 and n=1785, we get:
sqrt[(0.40*(1-0.40))/1785] = 0.014
Therefore, the sampling distribution of p has mean 0.40 and standard deviation 0.014.
c. To find the probability of obtaining a sample of 1785 adults in which 44% or more say they attended church last week, assuming the newspaper report's claim is true, we need to calculate the z-score and use a standard normal table or calculator to find the corresponding probability.
The z-score can be calculated using the formula:
z = (x - mu) / sigma
where x is the sample proportion, mu is the population proportion (given as 0.40), and sigma is the standard deviation of the sampling distribution (calculated as 0.014 above). Substituting x=0.44, mu=0.40, and sigma=0.014, we get:
z = (0.44 - 0.40) / 0.014 = 2.857
Using a standard normal table or calculator, we find that the probability of obtaining a z-score of 2.857 or higher is approximately 0.0021.
Therefore, the probability of obtaining a sample of 1785 adults in which 44% or more say they attended church last week, assuming the newspaper report's claim is true, is approximately 0.0021.
To know more about sampling distribution refer here :
https://brainly.com/question/29375938#
#SPJ11
The pair of points (-4, y) and (5, 7) lie on a line with slope 1/3
. What is the value of y?
Answers
Answer:
Step-by-step explanation:
(7 - y)/(5 + 4) = 1/3
(7 - y)/9 = 1/3
21 - 3y = 9
-3y = -12
y = 4
someone help me plsssss

Answers
p^5 / p^1/3
this is also p^(4 2/3)
To get this as a reciprocal, we multiply the exponent by -1. 1/p^(-4 2/3) A
Write the equation of a parabola that has a complex root at 4+5i and goes through the point (2,87)
Answers
Answer:
John is verey not smart
Step-by-step explanation:
Because he has fat
What is the image of (−7,−8) after a dilation by a scale factor of 44 centered at the origin?
Answers
Answer:
(-308, -352)
Step-by-step explanation:
For a dilation from the origin, you multiply the x and y by the scale factor.
-7 * 44 = -308
-8 * 44 = -352
(-308, -352)
ABCD is a parallelogram. Find z.

Answers
Step-by-step explanation:
here is the answer Step-by-step for you
I hope you understand...

Determine what type of transformation is represented help pls
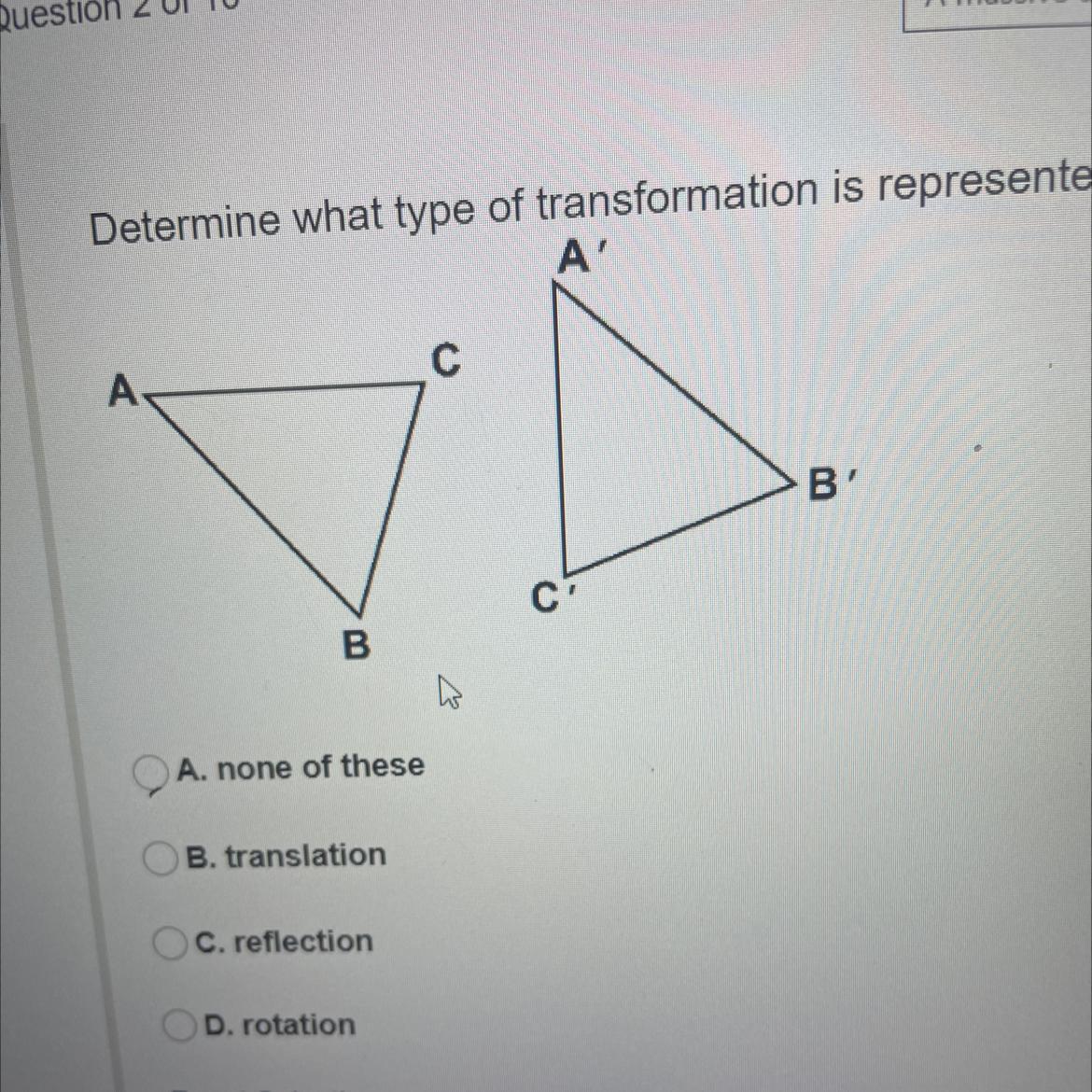
Answers
The type of transformation represented is rotation
Transformation of shapesTransformation techniques is the process of changing the position of an object on the xy-plane.
The transformation technique that we have include;
TranslationReflectionRotationFrom the diagram, you can see that the vertices ABC rotates clockwisely to generate the position A'B'C'. Hence the type of transformation represented is rotation
Learn more on rotation here: https://brainly.com/question/26249005
#SPJ1
suppose the true proportion of voters in the county who support a restaurant tax is 0.55. consider the sampling distribution for the proportion of supporters with sample size n
Answers
The mean of this distribution is 0.55
The standard error of this distribution is 0.0384
We have the following:
p=0.55
sample size, n=168
Mean of distribution:
Mean=true proportion of voters who support a restaurant
Mean=p=0.55
Hence, the mean of distribution is 0.55
Standard error of the distribution:
\(=\sqrt{\frac{p(1-p)}{n} }\)
\(=\sqrt{\frac{0.55(1-0.55)}{168} }\)
=0.0384
Hence, the standard error is 0.0384
Learn more about mean and standard error of distributions here:
https://brainly.com/question/14467769
#SPJ4
The questions was incomplete, the complete question is given below:
Suppose the true proportion of voters in the county who support a restaurant tax is 0.55. Consider the sampling distribution for the proportion of supporters with sample size n = 168.
What is the mean of this distribution?
What is the standard error of this distribution?
Using an integrating factor, solve y-y-5 CD- in the method for solving a first-order linear differential equation, the first step is to put the equation in the standard form y alty bit). is the given equation in the standard form? No Yes Identify a(t) and bit)
Answers
The value of a(t) is -1 and b(t) is 55 + \(e^t\)
No, the given equation y' - y = 55 + \(e^t\) is not in the standard form of a first-order linear differential equation.
In the method for solving a first-order linear differential equation, an integrating factor is a function used to transform the equation into a form that can be easily solved.
For an equation in the standard form y' + a(t)y = b(t), the integrating factor is defined as:
μ(t) = e^∫a(t)dt
To solve the equation, you multiply both sides of the equation by the integrating factor μ(t) and then simplify. This multiplication helps to make the left side of the equation integrable and simplifies the process of finding the solution.
To put it in standard form, we need to rewrite it as y' + a(t)y = b(t).
Comparing the given equation with the standard form, we can identify:
a(t) = -1
b(t) = 55 + \(e^t\)
Therefore, The value of a(t) is -1 and b(t) is 55 + \(e^t\)
Learn more about integrating factor here
https://brainly.com/question/32554742
#SPJ4
find the value of each of the lettered angles in the diagram below
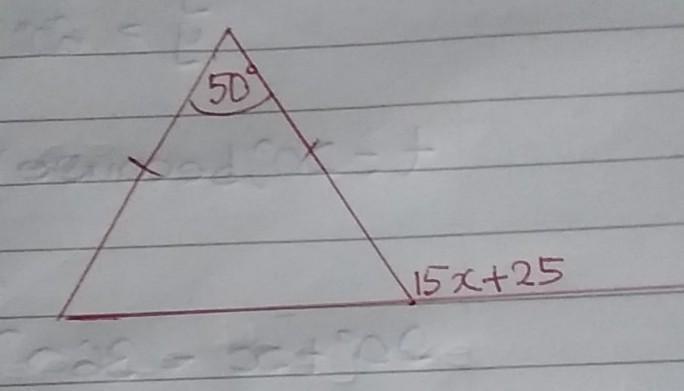
Answers
Answer:
Step-by-step explanation:
Remark
You have an isosceles triangle. That means that the angles opposite the marked sides are equal. So mark the angle on the lower left of the triangle as 50 degrees.
The solution to problem depends on the fact that the sum of the two inside angles of the triangle (each of which is marked as 50 degrees) not supplementary to the exterior angle, are still equal to the exterior angle.
Givens
<1 = 50 degrees
<2 = 50 degrees
Exterior angle = 15x + 25 Substitute the givens into the equation
Equation
<1 + <2 = 15x + 25
Solution
50 + 50 = 15x + 25 Combine the left side
100 = 15x + 25 Subtract 25 from both sides
100 - 25 = 15x + 25 - 25 Combine
75 = 15x Divide both sides by 15
75/15 = 15x/15
5 = x
Answer
<1 = 50 degrees
<2 = 50 degrees
15x + 25 = 75 + 25 = 100
Please Help me - You will get 60 points for the rapid reply- Use isosceles trapezoid ABCD to determine the following measurements-

Answers
Answer:
1) AD = 9 in
2) DE = 9.25 in
3) ∠EDC = 36°
4) ∠AEB = 108°
5) 11.5 in
Step-by-step explanation:
1) AD = BC = 9in
2) AC = BD (diagonals are equal)
⇒ BD = 14.25
⇒ BE + DE = 14.25
⇒ 5 + DE = 14.25
DE = 9.25
3) Since AB ║CD,
∠ABE = ∠EDC = 36°
4) ∠ABE = ∠BAE = 36°
Also ∠ABE + ∠BAE + ∠AEB = 180 (traingle ABE)
⇒ 36 + 36 + ∠AEB = 180
∠AEB = 108
5) midsegment = (AB + CD)/2
= (8 + 15)/2
11.5
Three more than a number j is at most 12
Answers
Answer:
j + 3 ≤ 12
Hope this helps :)
Solution, Explanation, & Check part below
Step-by-step explanation:
1. Isolate variable by doing the inverse operation which is subtracting 3 on both sides of the equation.
j + 3 ≤ 12
- 3 - 3
j ≤ 9
j can be any number that is less than 9 or equal to 9.
Check:
9 + 3 ≤ 12
12 ≤ 12
12 is equal to 12 ✓