Mrs. Bowlin organized the markers into sets. If there were 9 markers
in each set, how many sets of markers did Mrs. Bowlin create? there are 567 markers
Answers
Answer:
63 sets
Step-by-step explanation:
(567 markers)/(9 markers/set) = 567/9 sets = 63 sets
__
The total number of markers in all the sets (s) will be ...
9s = 567
Divide both sides of this equation by 9 to find the number of sets:
9s/9 = 567/9
s = 63
Mrs. Bowlin created 63 sets of markers.
Related Questions
What is a quartic function with only two real zeros of x=0 and x=4
Answers
The quartic function with only two real zeros of x=0 and x=4 is x² - 4x = 0
What is a quartic function?A quartic function is a quartic polynomial, that is, a polynomial with integer coefficients whose highest degree is four. The coefficient of the variable to the fourth degree cannot be zero. Examples of quartic functions include
From the roots;
a = 0 ; b = 4
From the polynomial expressions
x² - (a +b)x + ab = 0
x² - (0 +4 )x + 0*4 = 0
x² - 4x = 0
Learn more about quartic function at:https://brainly.com/question/25841119
#SPJ1
3
\(3 \sqrt{81} \)
what's the answer
Answers
Answer will be 27.
Given,
3√81
Now, to solve the expression the squares of whole numbers and square roots for some numbers must be known.
For example, squares of
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
Square roots,
√100 = 10
√81 = 9
√64 = 8
√49 = 7
√36 = 6
√25 = 5
√16 = 4
√9 = 3
√4 = 2
√1 = 1
Now ,
3√81 = 3× 9
= 27.
Thus the value is 27.
Know more about Square roots,
https://brainly.com/question/16113248
#SPJ1
An account pays 7% per year simple interest. In year 1, the amount in the
account is
$950. How much is in the account in year 6?
Answers
The amount in year 6 is $1282.5.
What is simple interest?
Simple interest is a quick and easy method of calculating the interest charge on a loan. Simple interest is determined by multiplying the daily interest rate by the principal by the number of days that elapse between payments.
Given,
rate of interest = 7%
time = 1 year
Amount on first year = $950
First we will calculate simple interest for 5 years, because amount is available for 1 year.
SI =PRT
SI = 950(7/100)1
SI = $332.5
Therefore, the amount after 6 years = 950+332.5
=$1282.5
To know more about simple interest, visit:
https://brainly.com/question/3942189
#SPJ1
I’m stuck on these questions

Answers
Answer:
Step-by-step explanation:
I) In the scatter graph question, D is the most suitable line of best fit for the data. Reason: the line diligently follow the points as they move upwards. Also, the points outside the line(i.e besides the line) are equally divided, on the up and down part of the line unlike in F
II) Here, you trace the values provided on the graph on one axis to get the corresponding value on the other axis.
Therefore, From the graph 600umbrellas = corresponds to 160 days.
III) Same rule in II) applies here.
28 lions = corresponds to 20 hyenas
IV) 50 cm = corresponds to 20kg weight
How many factors do numbers of the form p^n and q^m have if p and q are two different prime numbers and m and n are natural numbers?
Answers
The only common factor between these two numbers will be 1.
How many factors do these numbers share?
Remember that any number can be decomposed as a product of prime numbers. For example for 18 we have:
18 = 2*3*3
There 18 is written as a product of its prime factors.
Now, for our case of p^n and q^m we will have:
p^n = P = p*p*p...*p n times.
q^m = Q = q*q*q*...*q m times.
Now, notice that because q and p are primes, there is no common factor in these two decompositions. (and we can't decompose it furthermore). Then we conclude that the only factor that these numbers share is the trivial one, which is 1.
If you want to learn more about prime numbers, you can read:
https://brainly.com/question/145452
whats the remainder to 5,323 ÷ 34
Answers
Answer:
the answer is
Step-by-step explanation:
156.558 or 157.0
or
0.0060
Please help with this

Answers
Answer:
B
Step-by-step explanation:
No, because for x = 7, there are two values of y
Answer:
\(\huge\boxed{\sf No.}\)
Step-by-step explanation:
For a relation to act as a function, the x-values (domain) of the relation should NOT be repeated.
Here,
In domain(x-values), 7 is being repeated. Hence, the relation is not a function.
\(\rule[225]{225}{2}\)
In ms. Morales's class the ratio of boys to girls is 3:7. The class sizes at Ms.morales's school range from 22 to 34 students per class. What is the total number of students in Ms. Morales class
Answers
The total number of students in Ms. Morales's class is either 20 or 30, depending on the value of x.
Let the ratio of boys to girls in Ms. Morales's class be 3x:7x, where 3x represents the number of boys and 7x represents the number of girls.
The total number of students in the class is equal to the sum of the number of boys and the number of girls, which is 3x + 7x = 10x.
We don't know the value of x, but we do know that the class size is between 22 and 34 students.
Therefore, we can set up an inequality based on the total number of students:
22 ≤ 10x ≤ 34
Dividing all parts of the inequality by 10, we get:
2.2 ≤ x ≤ 3.4
Since x represents a whole number of students, the possible values for x are 3 (if there are 30 students in the class) or 2 (if there are 20 students in the class).
If x = 3, then the total number of students is:
10x = 10(3) = 30
If x = 2, then the total number of students is:
10x = 10(2) = 20
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
50,000 is 20% of what?
Answers
Answer:
250000
Step-by-step explanation:
20% of x is 50000
----------------------------
50000=20x/100
50000= x/5
5(50000) = x
250000 = x
Katie owns 2 2/3-acres of land. She divided the land into 1/3-acre lots. How many lots did Katie have?
Answers
Answer:
8 lots
Explanation:
1/3 into 2 2/3 is just division which is 8 lots
What is the slope of the following line?

Answers
Answer:c, the answer is c
Step-by-step explanation:
A square has a side length equal to 5x-3y inches. What is the area of this square

Answers
Answer:
D.
Step-by-step explanation:
The area is the product of 2 adjacent sides:
Area = (5x - 3y)(5x - 3y) as the sides of a square are all equal.
= 5x(5x - 3y) - 3y(5x - 3y)
= 25x^2 - 15xy - 15xy + 9y^2
= 25x^2 - 30xy + 9y^2.
3. [-/2 Points]
Find the limit of the function (if it exists). (If an answer does not exist, enter DNE.)
4x² + 5x-6
x+2
DETAILS
20
lim
X--2
Write a simpler function that agrees with the given function at all but one point. Use a graphing utility to confirm your result.
g(x)
LARCALC12 1.3.044.
Need Help? Read It
Answers
The limit of the function as x approaches -2 is 20.To find the limit of the function (if it exists), we can substitute the given value into the function and simplify. Given function: f(x) = 4x² + 5x - 6x + 2
To find the limit as x approaches -2, we substitute -2 into the function:
f(-2) = 4(-2)² + 5(-2) - 6(-2) + 2
= 4(4) - 10 + 12 + 2
= 16 - 10 + 12 + 2
= 20
Therefore, the limit of the function as x approaches -2 is 20.
To write a simpler function that agrees with the given function at all but one point, we can use a graphing utility. By plotting the given function and observing its behavior, we can create a simpler function that matches the original function except at one point.
However, without further information about the specific behavior of the given function, it is not possible to provide a more detailed explanation or a graph of the simpler function.
For more question on function
https://brainly.com/question/11624077
#SPJ8
John wishes to choose a combination of two types of cereals for breakfast - Cereal A and Cereal B. A small box (one serving) of Cereal A costs $0.50 and contains 10 units of vitamins, 5 units of minerals, and 15 calories. A small box (one serving) of Cereal B costs $0.40 and contains 5 units of vitamins, 10 units of minerals, and 15 calories. John wants to buy enough boxes to have at least 500 units of vitamins, 600 units of minerals, and 1200 calories. How many boxes of each cereal should he buy to minimize his cost?
Answers
Let's assume that John buys x boxes of Cereal A and y boxes of Cereal B. Then, we can write the following system of inequalities based on the nutrient and calorie requirements:
10x + 5y ≥ 500 (minimum 500 units of vitamins)
5x + 10y ≥ 600 (minimum 600 units of minerals)
15x + 15y ≥ 1200 (minimum 1200 calories)
We want to minimize the cost, which is given by:
0.5x + 0.4y
This is a linear programming problem, which we can solve using a graphical method. First, we can rewrite the inequalities as equations:
10x + 5y = 500
5x + 10y = 600
15x + 15y = 1200
Then, we can plot these lines on a graph and shade the feasible region (i.e., the region that satisfies all three inequalities). The feasible region is the area below the lines and to the right of the y-axis.
Next, we can calculate the value of the cost function at each corner point of the feasible region:
Corner point A: (20, 40) -> Cost = 20
Corner point B: (40, 25) -> Cost = 25
Corner point C: (60, 0) -> Cost = 30
Therefore, the minimum cost is $20, which occurs when John buys 20 boxes of Cereal A and 40 boxes of Cereal B.
Which fractions have a LCD of 30?
A 3/4, 1/7, 1/6
B 2/3, 1/5, 1/15
C 2/15, 1/4, 1/3
D 2/3, 1/6, 1/5
Answers
Answer:
B
Step-by-step explanation:
2/3, 1/6, and 1/5 fractions have an LCD of 30 which is correct option(D).
What is LCD?The lowest common denominator is defined as the set of fraction denominators with the lowest common multiple. The lowest positive integer with more than one denominator in the set is LCD.
LCD by division of prime numbers
(D) 2/3, 1/6, 1/5
The factors of the denominators 3, 6, 5
3 = 3 x 1
6 = 3 x 2 x 1
5 = 5 x 1
The LCD = 3 x 2 x 5 = 30
Hence, 2/3, 1/6, and 1/5 fractions have an LCD of 30.
Learn more about the lowest common denominator here:
https://brainly.com/question/8413590
#SPJ2
Given the function f(x) = 3x - 1, explain how to find the average rate of change between x = 1 and x = 4.
Answers
Step-by-step explanation:
f(1) = 3×1 - 1 = 2
f(4) = 3×4 - 1 = 12-1 = 11
so, the functional value changes 11-2=9 units on an x interval of 4-1=3 units length.
the average change rate is the total change across the x interval relative to the interval length.
that is
9/3 = 3
which is the slope (= the factor of x) in the line equation.
for a line its change rate for any point is the same constant. and that is therefore automatically also the average change rate across an interval of x values.
if the change rate would be different for different parts of the function, it would not be a straight line.
Answer:
3
Step-by-step explanation:
The average rate of f(x) in the closed interval [ a, b ] is
\(\frac{f(b)-f(a)}{b-a}\)
Here [ a, b ] = [ 1, 4 ] , then
f(b) = f(4) = 3(4) - 1 = 12 - 1 = 11
f(a) = f(1) = 3(1) - 1 = 3 - 1 = 2
average rate of change = \(\frac{11-2}{4-1}\) = \(\frac{9}{3}\) = 3
3. Find the x-intercept of y = 3.
(3,0)
(0,3)
(3,3)
O no x-intercept
Answers
Answer:
3
Step-by-step explanation:
x-y =3
To find the x intercept, set y=0
x-0 =3
x=3
Step-by-step explanation:
Answer:
x=(3,0)
Step-by-step explanation:
hope this helps
Please look at the pic and help!!

Answers
Answer:
4x² + 22x - 12
Step-by-step explanation:
A = bh/2
A = (4x - 2)(2x + 12)/2
A = (8x² + 48x - 4x - 24)/2
A = (8x² + 44x - 24)/2
A = 4x² + 22x - 12
arccsc(\(\frac{2}{3}\)\(\sqrt{3}\))
Answers
The arc cossecant of the given value is of 30º.
Cosecant and arc cosecantThe cosecant of an angle is given by the ratio between 1 and the sine of the angle, as follows:
cos(x) = 1/sin(x)
The arc cossecant of an angle is represented by the expression arc csc(x), and represents the inverse of the cossecant, that is, it is the angle which has a cosecant of x.
In this problem, the arc cossecant that is asked is:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)}\)
Basically, it asks for the angle which has a cossecant value of 2/(3sqrt(3)). This angle is found using a calculator, and it is of 30º.
Hence the numeric value of the expression is presented as follows:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)} = 30^\circ\)
More can be learned about cossecant and arc cossecant at https://brainly.com/question/13276558
#SPJ1
5x−2y−4=0
3x+16y−54=0
Answers
Answer:
X = 2
Y = 3
Step-by-step explanation:
\(5(8)x - 2(8)y - 4(8) = 0 \\ + \\ 3x + 16y - 54 = 0 \\ = \\43x - 86 = 0 \\ 43x = 86 \\ x = 86 \div 43 \\ x = 2 \\ 5(2) - 2y - 4 = 0 \\ 10 - 2y - 4 = 0 \\ 6 - 2y = 0 \\ 2y = 6 \\ y = 6 \div 2 \\ y = 3\)
I need answer fast plz

Answers
Answer:
a+5b-35
Step-by-step explanation:
= 5(1/5atb-7) MULTIPLY THE PARENTHESES BY 5
= 5x1/5 a+5b-5x7 REDUCE MULTIPLY
= a+5b-35
Answer:
A + 5b - 35
Step-by-step explanation:
M A T H W A Y
Assume that military aircraft use ejection seats designed for men weighing between 132. 4132. 4 lb and 217217 lb. If women's weights are normally distributed with a mean of 168. 7168. 7 lb and a standard deviation of 48. 848. 8 lb, what percentage of women have weights that are within those limits
Answers
The percentage of women with weights that are within the limits is:
60.93%
What percentage of women have weights that are within those limits?Can be calculated using the normal distribution formula. First, we need to find the z-scores for both the lower and upper limits:
z-score for lower limit = (132.4 - 168.7) / 48.8 = -0.74
z-score for upper limit = (217 - 168.7) / 48.8 = 0.99
Next, we can use a z-table to find the corresponding probabilities for these z-scores:
Probability for lower limit = 0.2296
Probability for upper limit = 0.8389
Finally, we can subtract the lower probability from the upper probability to find the percentage of women with weights that are within those limits:
Percentage = 0.8389 - 0.2296 = 0.6093
Therefore, approximately 60.93% of women have weights that are within the limits of 132.4 lb and 217 lb.
More information about the percentage here: https://brainly.com/question/28952121
#SPJ11
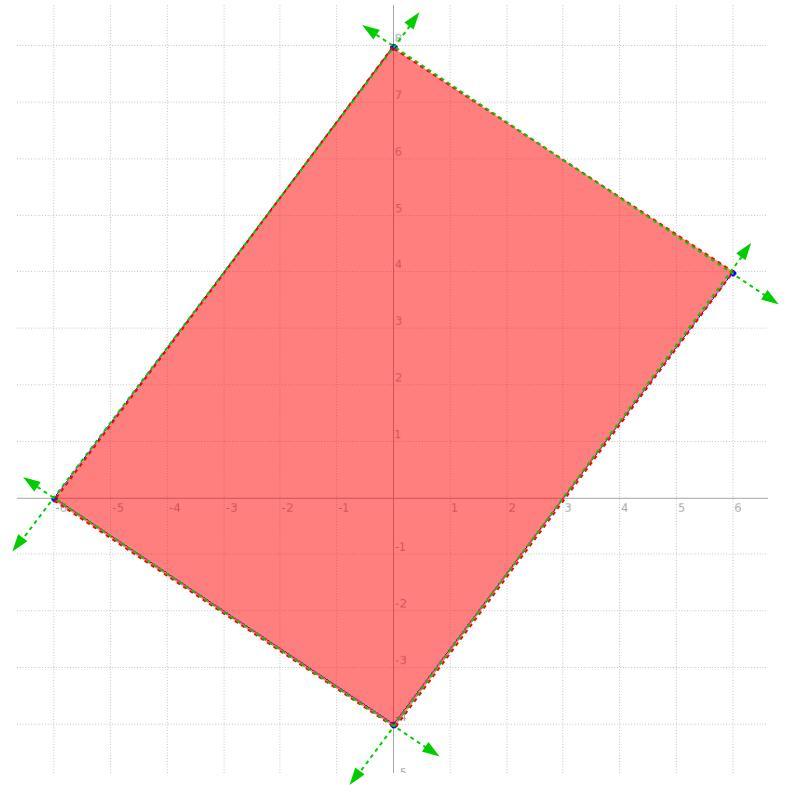
HELP PLEASE I DONT GET THIS

Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
Solve for h. Please show work.

Answers
Answer: 3.75 ft
Step-by-step explanation:
30/8=3.75
So since area is A= L*W
8*3.75=30 ft2
A coach of a baseball team orders hats for
the players on his team. Each hat costs
$9.95. The shipping charge for the entire
order is $5.00. There is no tax on the order.
The total cost of the coach's order is less
than $125.00. Which inequality can be
used to determine the greatest number of
hats, h, the coach orders?
Answers
Answer:
9.95h + 5 ≤ 125
Step-by-step explanation:
let 'h' = number of hats
Insert Parentheses to make the equality true. 1+2x3+4x5=29
Answers
Answer:
((1+2)x3) + (4x5) = 29
Step-by-step explanation:
Since 4x5 = 20 and 3x3 = 9, and 9 + 20 = 29, we put parenthesis around 1+2,
we get,
((1+2)x3) + (4x5) = 29
This is true because,
(3x3) + (4x5) = 29
(9) + (20) = 29
29 = 29
A student claims that 0.304 = 0.34 because 0 is nothing. How do you respond?
Answers
Answer:
0 equals to nothing when it is found before a number that does not have a decimal
exqmple: 037 , 048 , 089 ect.
or when the zero is behind a decimal by itself
example: 35.0 23.0 54.0
Ryan is a runner. He can run 100 meters in 13 seconds. He
frequently races against Juan, who can run at a speed of 15
miles per hour. Which runner is faster? (1 mile = 1609.34
meters)

Answers
Answer:
Ryan: (100/13)(1/1,609.34)(3,600) =
17.21 miles per hour
Ryan is faster than Juan, by about 2.21 miles per hour
(02.02 MC)
If trapezoid ABCD was reflected over the y-axis, reflected over the x-axis, and rotated 180°, where would point A′′′ lie?
Trapezoid formed by ordered pairs A at negative 4, 1, B at negative 3, 2, C at negative 1, 2, D at 0, 1.
(1, −1)
(−4, 1)
(1, 1)
(−4, −1)
Answers
The location of point A''' after the three transformations would be (-4, 1).
To determine the location of point A''', we need to apply the three transformations (reflection over the y-axis, reflection over the x-axis, and rotation of 180°) to point A.
When a point is reflected over the y-axis, the x-coordinate is negated while the y-coordinate remains the same.
So, the reflection of point A (-4, 1) over the y-axis would be (4, 1).
When a point is reflected over the x-axis, the y-coordinate is negated while the x-coordinate remains the same. So, the reflection of point (4, 1) over the x-axis would be (4, -1).
When a point is rotated 180°, the x-coordinate and y-coordinate are both negated. So, the rotation of point (4, -1) by 180° would be (-4, 1).
To learn more on Transformation click:
https://brainly.com/question/11709244
#SPJ1
Please look at the photo for the question. Thank you!

Answers
The function g(x) = x² + 4x has a: A. minimum.
The minimum value occur at x = -2.
The function's minimum value is -4.
How to determine the axis of symmetry and vertex of a quadratic function?In Mathematics, the axis of symmetry of a quadratic function can be calculated by using this mathematical equation:
Axis of symmetry = -b/2a
Where:
a and b represents the coefficients of the first and second term in the quadratic function.
For the given quadratic function g(x) = x² + 4x, we have:
a = 1, b = 4, and c = 0
Axis of symmetry, Xmax = -b/2a
Axis of symmetry, Xmax = -(4)/2(1)
Axis of symmetry, Xmax = -2
Next, we would determine vertex as follows;
g(x) = x² + 4x
g(-2) = -(-2)² + 4(-2)
g(-2) = -4.
Read more on quadratic functions here: brainly.com/question/14201243
#SPJ1