Answers
Step-by-step explanation:
well, the starting equation and the target format have been given.
let's do the multiplications and compare the target with the starting information.
from there we see what is different or missing.
x² + 14x + 13 = 0
and
(x - p)² = q
x² - 2px + p² = q
x² - 2px + (p² - q) = 0
now let's compare the different parts :
x² = x²
-2px = 14x
-2p = 14
p = -7
p² - q = 13
-7² - q = 13
49 - q = 13
36 - q = 0
q = 36
so, the square (x - p)² = (x + 7)² is completed when
x² + 14x + 49 = 0
but we have only "+ 13". so we need to add 36 to get 49. but we need to do it on both sides, to keep the equation true :
x² + 14x + 13 + 36 = 36
x² + 14x + 49 = 36
(x + 7)² = 36
just as we calculated already above.
and now this can be solved by pulling the square root on both sides (a quadratic equation has always 2 solutions)
x + 7 = ±6
x1 = 6 - 7 = -1
x2 = -6 - 7 = -13
Related Questions
Use the distributive property to write the following expressions in expanded form.
5 (7h + 3m)
Answers
Answer: Did it in ways that are different.
Step-by-step explanation:
35.25 hours
2115 minutes
5 3 minutes + 5 7 hours
The range of some numbers is 5.
What happens to the range if the numbers are increased by 3?
Answers
Answer:
the range does not change
Step-by-step explanation:
The range in the difference between the greatest and the smallest numbers.
If all numbers are increased by 3, the difference between the greatest and the smallest remains the same, so the range remains the same.
Answer: the range does not change
If the numbers are increased by 3, the range remains unchanged i.e. 5
How to determine the range?Assume the smallest and the largest numbers are x and y.
So, the range is:
R = y - x
When the numbers are increased by 3, the smallest and the largest numbers become x + 3 and y + 3
So, the range is:
R = y + 3 - x - 3
Evaluate the sum
R = y - x
Notice that the expression for range in both scenarios are the same.
Hence, if the numbers are increased by 3, the range remains the same
Read more about range at:
https://brainly.com/question/14532771
What is the value of x in the pentagon above?

Answers
The sum of the interior angles of a pentagon is 540°.
We can use this information to find the value of x by adding the rest of the interior angles and then substracting them from 540°:
\(\begin{gathered} 90+90+100+105+x=540 \\ 385+x=540 \\ x=540-385 \\ x=155 \end{gathered}\)It means that the correct answer is b. 155.
Which expression is equivalent to the following complex fraction?
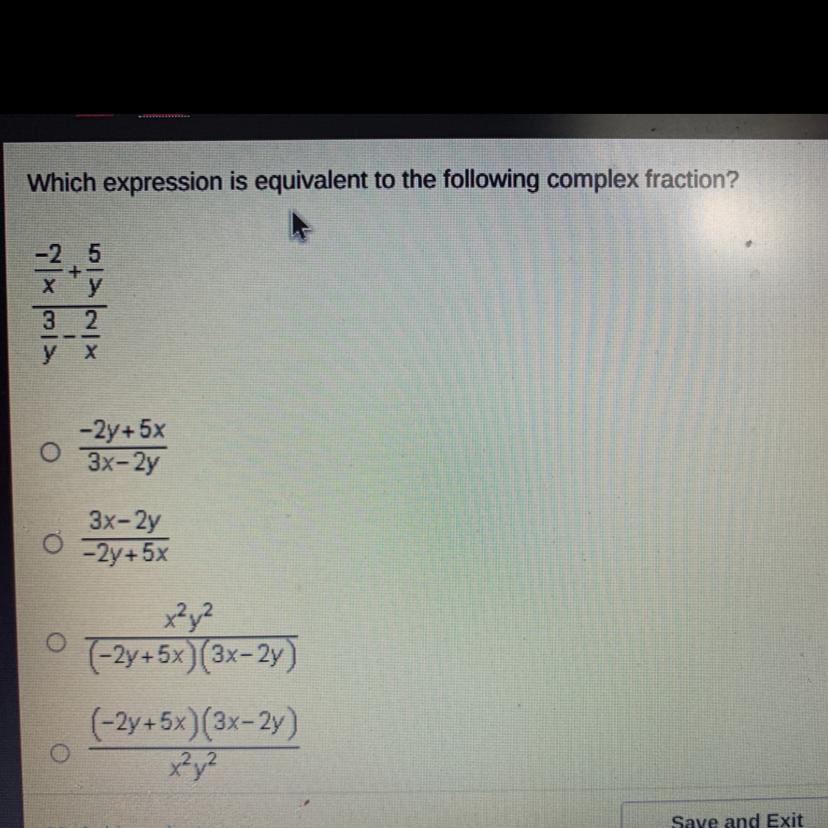
Answers
Answer:
\(\frac{ - 2x + 5x}{3x - 2y}\)
Step-by-step explanation:
\( \frac{ \frac{ - 2}{x} + \frac{5}{y} }{ \frac{3}{y} - \frac{2}{x} } = \frac{ \frac{ - 2y + 5x}{xy} }{ \frac{3x - 2y}{xy} } \\ = \frac{ - 2y + 5x}{xy} \times \frac{xy}{3x - 2y} \\ = \frac{ - 2x + 5x}{3x - 2y} \)
solve the differential equation for the motion of the spring 375d2xdt2 450dxdt 135x=0 if x(0)=−1 dxdt∣∣t=0=4 x(t)= this spring is critically damped, will it go past equilibrium?
Answers
The solution to the differential equation for the motion of the spring is x(t) = (c1+ c2t) \(e^-\frac{3t}{5}\), where c1 and c2 are constants determined by the initial conditions x(0) = -1 and dx/dt|t=0=4.
Since the spring is critically damped, it will not go past equilibrium as it returns to its equilibrium position without oscillating.
To solve the given differential equation, we first find the characteristic equation by replacing d²x/dt² with r², dx/dt with r, and x with 1: 375r² + 450r + 135 = 0.
Solving for r using the quadratic formula gives r = -0.6 and r = -0.9. Since the roots are equal, the general solution is x(t) = (c1 + c2t) \(e^-\frac{3t}{5}\), where c1 and c2 are constants determined by the initial conditions.
Using x(0) = -1, we get c1 = -1. To find c2, we differentiate x(t) with respect to t and use the initial condition dx/dt|t=0=4, giving c2 = 4. Thus, the solution is x(t) = (-1 + 4t) \(e^-\frac{3t}{5}\) .
Since the spring is critically damped, the damping coefficient is equal to the undamped natural frequency, which means that it returns to equilibrium as quickly as possible without oscillating. Therefore, the spring will not go past equilibrium.
To know more about differential equation click on below link:
https://brainly.com/question/14620493#
#SPJ11
Find the domain and range for each of the relations described by the sets of
ordered pairs below.
4. (-1, 2), (2, 51), (1,3), (8, 22), (9,51)
Domain:
Range:
Answers
Answers:
Domain = {-1, 2, 1, 8, 9}
Range = {2, 51, 3, 22}
==================================
Explanation:
The domain is the set of allowed inputs of a function. So it's the set of possible x values. We simply list the x coordinates of each point to form the domain.
The range is the set of possible y values or y outputs. So we simply list the y coordinates of the points. We toss out any duplicates. Since order doesn't matter in a set, we can have the values listed any way we want.
Side notes:
This is a function since we don't have any repeated x values between any of the points. This graph passes the vertical line test.This function is not one-to-one because we have y = 51 correspond to multiple x values (x = 2 and x = 9 simultaneously). This graph fails the horizontal line test.URGENT PLEASE HELP I DONT UNDERSTAND
You receive bids for making T-shirts for your class fundraiser from four companies. To
present the pricing information, one company uses a table, one company uses a written
description, one company uses an equation, and one company uses a graph. How will
you compare the different representations and make the final choice?
The design is ready, and your job is to select the best option for ordering the shirts. The
proposals from the four companies are listed below. Another slight problem is that the
class officers have not decided how many T-shirts you should order.
Part 1:
Compare your options and explain which company you would select for orders from
20 to 200 T-shirts. Explain your reasoning clearly by using the correct terminology.




Answers
Answer:
Step-by-step explanation:
2\
a group contains n men and n women. how many ways are there to arrange these people in a row if the men and women alternate and the first person in the row is the youngest one?
Answers
If there are n men and n women in the group, we can first arrange the men and women separately in alternate positions. We can treat the men as a single group and arrange them in n! ways, and similarly, we can treat the women as a single group and arrange them in n! ways.
Next, we need to arrange the two groups (men and women) in alternate positions to satisfy the given condition. Since we need to place the youngest person (who could be a man or a woman) at the beginning of the row, we have two cases:
Case 1: The youngest person is a man
In this case, the men must start the arrangement, followed by the women. Since there are n men and n women, there are n! ways to arrange the men and n! ways to arrange the women. We can fix the youngest man at the beginning of the row, so there are (n-1)! ways to arrange the remaining n-1 men. Similarly, there are (n-1)! ways to arrange the n-1 women. Therefore, the total number of arrangements in this case is:
n! * n! * (n-1)! * (n-1)!
Case 2: The youngest person is a woman
In this case, the women must start the arrangement, followed by the men. Since there are n women and n men, there are n! ways to arrange the women and n! ways to arrange the men. We can fix the youngest woman at the beginning of the row, so there are (n-1)! ways to arrange the remaining n-1 women. Similarly, there are (n-1)! ways to arrange the n-1 men. Therefore, the total number of arrangements in this case is:
n! * n! * (n-1)! * (n-1)!
To get the total number of arrangements that satisfy the given condition, we need to add the number of arrangements in Case 1 and Case 2:
n! * n! * (n-1)! * (n-1)! + n! * n! * (n-1)! * (n-1)!
= 2 * n! * n! * (n-1)! * (n-1)!
= 2 * (n!)^2 * (n-1)!
Therefore, the total number of ways to arrange the people in a row with alternating men and women, starting with the youngest person, is 2 * (n!)^2 * (n-1)!.
this square-based oblique pyramid has a volume of 125\text{ m}^3125 m 3 125, start text, space, m, end text, cubed
Answers
Given that the volume of a square-based oblique pyramid is 125 m³ and the square base has sides of 5 meters, we can calculate the height of the pyramid using the formula for the volume of a pyramid. The height of the pyramid is approximately 25 meters.
The volume of a pyramid is given by the formula V = (1/3) * A_base * h, where A_base is the area of the base and h is the height of the pyramid. In this case, the volume is given as 125 m³, and the base is a square with sides of 5 meters. The area of a square base is calculated by squaring one of the sides, so A_base = 5² = 25 m².
We can substitute the known values into the volume formula:
125 = \(\frac{1}{3} * 25 * h\)
To solve for h, we can rearrange the equation:
125 = \(\frac{25}{3} * h\)
h = \(\frac{(125 * 3)}{25}\)
h = 15 * 3
h =45
Therefore, the height of the pyramid is approximately 45 meters.
Know more about Pyramid here: https://brainly.com/question/33473833
#SPJ11
The complete question is: this square-based oblique pyramid has a volume of 125\text{ m}^3125 m 3 125, start text, space, m, end text, cubed. a slanted pyramid with a square base. the square base has sides of five meters. a slanted pyramid with a square base. the square base has sides of five meters. what is the height of the pyramid?
A survey of statistics undergraduate at prosperity university completed a survey that asked for their verbal and math sat scores. They wanted to predict the verbal score based on the math score. Interpret the slope.
Answers
The slope in the context of predicting verbal SAT scores based on math SAT scores indicates the change in the verbal score for each unit increase in the math score.
In this survey of statistics undergraduate students at Prosperity University, the slope represents the rate of change in the verbal SAT score for every one-point increase in the math SAT score. A positive slope suggests that as the math score increases, the verbal score also tends to increase. The magnitude of the slope indicates the strength of the relationship between the two variables. A larger slope indicates a stronger positive association, meaning that a one-point increase in the math score is associated with a larger increase in the verbal score. Conversely, a negative slope would imply an inverse relationship, where an increase in the math score is associated with a decrease in the verbal score.
Learn more about SAT score here
brainly.com/question/32449961
#SPJ11
What is the interpretation of the slope in the context of predicting the verbal SAT score based on the math SAT score, according to the survey conducted among undergraduate students majoring in statistics at Prosperity University?
What does closed under addition mean in math?
Answers
The sum of two integers is also an integer.
What is an integer?
Zero, a positive natural number, or a negative integer denoted by a minus sign are all examples of integers. The inverse additives of the equivalent positive numbers are the negative numbers. The boldface Z is a common way to represent the set of integers in mathematical terms.
When we conduct an operation on set members and always obtain a set member, the set is said to be closed under that operation. As a result, a set either possesses closure regarding a particular operation or it does not. A set is said to satisfy a closure property if it is closed by an operation or set of operations. A closure property is typically introduced as a hypothesis, known as the axiom of closure.
If a and b two integer.
Then the sum of the integer a + b is also an integer. Thus addition operation closer property.
To learn more about closer property, click on below link:
https://brainly.com/question/29798480
#SPJ4
Here is a rectangle with length 5 units and width 2 units.
1. What is the area of the rectangle?
2. Dilate rectangle ABCD from point A by a scale factor of 2. Calculate the area of the image.
3. Dilate rectangle ABCD from point A by a scale factor of 3. Calculate the area of the image.

Answers
This refers to the ratio between the scale of a given original object and a new object. It is its representation but of a different size (bigger or smaller). For example, if we have a rectangle of sides 2 cm and 4 cm, we can enlarge it by multiplying each side by a number, say 2.
Solving for the area and scale factor we have:
L= 5 units
W = 2 units
The area of the rectangle =L * WA = (5 x 2)
A = 10 square units.
If the rectangle is dilated from point A by a scale factor of 2, the area of the image:A= (Scale factor of L * W)* L * W
= (2 x 2 x 5 x 2)
A = 40 square units.
If the rectangle is dilated from point A by a scale factor of 3, the area of the image is:A= (Scale factor of L * W)* L * W
= (3 x 3 x 5 x 2)
A= 90 square units
Learn more about area on
https://brainly.com/question/29082330
#SPJ1
Use Euler's Method with a step size of h = 0.1 to find approximate values of the solution at t = 0.1,0.2, 0.3, 0.4, and 0.5. +2y=2-ey (0) = 1 Euler method for formula Yn=Yn-1+ hF (Xn-1-Yn-1)
Answers
Using Euler's Method with a step size of h = 0.1, the approximate values of the solution at t = 0.1, 0.2, 0.3, 0.4, and 0.5 are:
t = 0.1: y ≈ 1.1
t = 0.2: y ≈ 1.22
t = 0.3: y ≈ 1.34
t = 0.4: y ≈ 1.47
t = 0.5: y ≈ 1.61
To use Euler's Method, we start with an initial condition. In this case, the given initial condition is y(0) = 1. We can then iteratively calculate the approximate values of the solution at each desired time point using the formula:
Yn = Yn-1 + h * F(Xn-1, Yn-1)
Here, h represents the step size (0.1 in this case), Xn-1 is the previous time point (t = Xn-1), Yn-1 is the solution value at the previous time point, and F(Xn-1, Yn-1) represents the derivative of the solution function.
For the given differential equation +2y = 2 - ey, we can rearrange it to the form y' = (2 - ey) / 2. The derivative function F(Xn-1, Yn-1) is then (2 - eYn-1) / 2.
Using the initial condition y(0) = 1, we can proceed with the calculations:
t = 0.1:
Y1 = Y0 + h * F(X0, Y0)
= 1 + 0.1 * [(2 - e^1) / 2]
≈ 1 + 0.1 * (2 - 0.368) / 2
≈ 1 + 0.1 * 1.316 / 2
≈ 1 + 0.1316
≈ 1.1
Similarly, we can calculate the approximate values of the solution at t = 0.2, 0.3, 0.4, and 0.5 using the same formula and previous results.
Using Euler's Method with a step size of h = 0.1, we found the approximate values of the solution at t = 0.1, 0.2, 0.3, 0.4, and 0.5 to be 1.1, 1.22, 1.34, 1.47, and 1.61, respectively.
To know more about Euler's Method visit:
https://brainly.com/question/32691755
#SPJ11
A data set will always have exactly one mode.
O True O False
Answers
False. A data set may have one mode, but it is also possible for a data set to have no mode or multiple modes.
What is the mode of data?A mode of data is defined as an observation with the highest frequency among the values that appear most frequently in the given data.
If no value is repeated, the dataset has no mode. If two or more values appear with the same maximum frequency, then the dataset has multiple modes.
For example, consider the following dataset:
1, 2, 3, 3, 4, 4, 5
In this dataset, both 3 and 4 appear twice, which means that the dataset has multiple modes.
So, in general, it is not always true that a data set will have exactly one mode. It depends on the values in the dataset and their frequencies.
Therefore, the correct answer would be option (B) False.
Learn more about the mode of data here:
brainly.com/question/300591
#SPJ2
Find the zero places of the quadratic function: y= x^2 + 5x + 6
Answers
The required zero places of the given equation y= x² + 5x + 6 is x = -2 and x = -3.
Given that,
An equation y= x² + 5x + 6,
To determine the Zeros of the equation given above.
The equation is the relationship between variables and is represented as y =ax + b is an example of a polynomial equation.
Here, given equation is, y= x² + 5x + 6
Now, let y = 0
x² + 5x + 6 = 0
x² + 2x + 3x + 6 = 0
x(x + 2) + 3 (x + 2) = 0
(x + 2) * (x + 3) = 0
x + 2 = 0 ; x + 3 = 0
x = -2 and x = -3
Thus, the required zero places of the given equation y= x² + 5x + 6 is x = -2 and x = -3.
Learn more about the equation here:
brainly.com/question/10413253
#SPJ1
Solve by factoring the equation

Answers
Answer:
x=-5/3 and x= 1/4
Step-by-step explanation:
Subtract 5 to both sides and then get 12x^2+17x-5=0. Then rewrite the difference for 17x so 20x-3x. Your equation will look like this 12x^2+20x-3-5=0. Now factor 4x out of 12x² ad 20x and get 4x(3x+5). Now factor 3x+5 ad get (4x-1). Now set (3x+5)=0 and (4x-1)=0 and now you will get -5/3 and 1/4.
[10 points] Find the number of ways of arranging the letters of EQUATION, so that all the vowels are in alphabetical order.
Answers
Answer: The number of ways of arranging the letters of EQUATION, so that all the vowels are in alphabetical order = 336 .
Step-by-step explanation:
Given word = "EQUATION"
Total letters = 8
Total Vowels (EUAIO)=5
Total number of ways to arrage letters = 8!
Number of ways to arrange vowels in alphabetical order = 5!
Then, The number of ways that all the vowels are in alphabetical order will be :
\(\dfrac{8!}{5!}=\dfrac{8\times7\times6\times5!}{5!}=336\)
Hence, the number of ways of arranging the letters of EQUATION, so that all the vowels are in alphabetical order = 336 .
Jones invests only a part of his wealth into a risky asset that has a positive return of 10% with probability π and has a negative return of −4% with probability 1−π. The risk-free rate is 1%. Jones' utility function is u=ln(w), where w is his wealth. Which of the following is true about π ?
a. 0.2857≤π≤0.358
b. 0.388≤π≤1
c. 0.357≤π≤0.389
d. None of the above
Answers
Option a is correct. we are given that Jones invests only a part of his wealth into a risky asset that has a positive return of 10% with probability π and has a negative return of −4% with probability 1−π.
The risk-free rate is 1%. Jones' utility function is u=ln(w), where w is his wealth.
Let us solve the problem: Let x be the fraction of Jones’ wealth that he invests in the risky asset. Thus, (1 - x) is the fraction he invests in the risk-free asset.:
\(U = x * ln(1 + 10%) + (1 - x) * ln(1 + 1%) = x * ln(1.1) + (1 - x) * ln(1.01)\)
Let EV be the expected value of his investment. Thus, we have:
\(E(V) = x * 10% + (1 - x) * 1% = 9% * x + 1%\)
Let us assume that Jones invests enough of his wealth in the risky asset so as to make it the optimal portfolio. This means that the expected utility from the investment in the risky asset equals the expected utility from the risk-free asset. Mathematically,
\(x * ln(1.1) + (1 - x) * ln(1.01) = ln(w)\)
On solving this equation, we get x =\((ln(w) - ln(1.01)) / (ln(1.1) - ln(1.01)) = ln(w) - ln(1.01) / ln(1.1) - ln(1.01)\)
Let us assume that Jones invests at least part of his wealth in the risky asset. Thus,\(0 ≤ x ≤ 1\). This means that \(0 ≤ π ≤ 1\).
The correct option is a.\(0.2857 ≤ π ≤ 0.358\).
To know more about probability visit:-
https://brainly.com/question/31828911
#SPJ11
HELP!!! 13
*NOT A TEST*

Answers
Answer: 4 Area Codes/year
Step-by-step explanation:
1996 171
2007 215
CHANGE:
11 years
44 additional codes
44 Codes/11 years = 4 codes/year
help me please please

Answers
Answer:
(x - 2)² + (y +8)² = 4Step-by-step explanation:
Equation of circle:\(\sf\boxed{(x-h)^2+(x-k)^2=r^2}\)
Here, h , k are the co ordinates of the center and r is the radius
\(\sf (x - 2)^2 + (y-[-8])^2 = 2^2\\\\(x - 2)^2 + (y + 8)^2= 4\)
Of all rectangles with a perimeter of 10 meters, which one has the maximum area? (Give both the dimensions and the area enclosed)
Answers
Zone(area) = L x W = 2.5 x 2.5 = 6.25 square meters.
Of all rectangles with an edge of 10 meters, the one that has the greatest zone(area) could be a square.
To see why, let's assume that a rectangle with a border of 10 meters has measurements of length L and width W.
At that point, we know that:
2L + 2W = 10
Rearranging this condition, we get:
L + W = 5
Presently, we need to discover the most extreme range encased by the rectangle, which is given by:
Area = L x W
Able to illuminate for one variable in terms of the other utilizing the condition L + W = 5:
L = 5 - W
Substituting this expression for L into the condition for the zone, we get:
Zone = (5 - W) x W
Extending and disentangling this expression, we get:
Area = 5W - W²
To discover the most extreme esteem of this quadratic expression, we will take its subsidiary with regard to W and set it to break even with zero:
dArea/dW = 5 - 2W =
Tackling for W, we get:
W = 2.5
Substituting this esteem back into the condition for the edge, we get:
L = 2.5
Hence, the measurements of the rectangle that has the greatest region are L = 2.5 meters and W = 2.5 meters, which implies it could be a square. The most extreme zone enclosed by the rectangle is:
Zone(area) = L x W = 2.5 x 2.5 = 6.25 square meters.
To know more about rectangles refer to this :
https://brainly.com/question/2607596
#SPJ4
The lengths of parallel chords which are on opposite sides of the Centre of a
circle are 24 cm and 10 cm. If radius of the circle is 13 cm, then the distance
between these chords is ...............
A) 12 cm B) 10 cm C) 17 cm D) 8 cm
Answers
The distance between these chords is 12cm
Chord and circlesTo get the distance between the chords, we will use the Pythagoras theorem as shown:
Let the required distance be "d"
The radius of th circle = 13 cm (hypotenuse)Adjacent side = 10/2 = 5cmAccording to the theorem:
\(13^2=d^2+5^2\\ d^2=13^2-5^2\\ d^2=169-25\\ d^2=144\\ d =12cm\)
Hence the distance between these chords is 12cm
Learn more on chords here: https://brainly.com/question/13598644
Thank non so much Chene Inters! thank nen so much Chene Inters! Thank nen semneh Chena inters! That en so much Chean Inters! Thank nen so much Chean Inters! thank nen remneh Chene Inters! Thank you so much Cheos tuters! Thank you so much Cheas tuters! thank you so much Cheao tutor thank you so much Cheos tuters! Thank you so much Cheos tuters! Thank you so much Cheas tuter This is This is The The QuestioQuestion I need I need Help Help With: With: This is This is The The QuestioQuestion I need I need Help Help Write a Regular Expression For this With: With: This is This is The The Questionuestion I need I need Help Help With: With: This is This is language: The Question L = {w = {a,b}* | w has I need Help With: This is odd number of The Question I need a's and ends Help With: This is The Question I need Help With: This is The The Question Question need with b} Please show work neatly and I will thumb up your answer promptly if it makes sense! Do not copy and paste work from other questions or I will give you a thumbs down. I need Help With: Help With: This is This is The The Question Question I need I need Help With: Help
Answers
The regular expression is ^(a(aa)*b)$.
Find Regular expression for odd 'a's, ending with 'b'?To create a regular expression for the language L = {w = {a,b}* | w has an odd number of 'a's and ends with 'b'}, we can use the following expression:
^(b|(a(aa)*b))$
Breaking it down:
^ indicates the start of the string.
(b|(a(aa)*b)) matches either 'b' or a sequence of 'a's followed by an odd number of 'a's and 'b'.
(aa)* matches zero or more pairs of 'a's.
$ indicates the end of the string.
This regular expression ensures that the string starts with 'b' or a sequence of 'a's, followed by an odd number of 'a's, and ends with 'b'. Any additional characters or sequences in between are not allowed.
Please note that regular expressions can have different notations and conventions depending on the context or programming language you're using. The expression provided here follows a general pattern that should work in most cases.
Learn more about Regular Expression
brainly.com/question/32344816
#SPJ11
Write 3x 1/2 in radical form
Answers
Answer:
3x^1/2 in radical form is
\( \sqrt{3x} \)
Hope this helps you
if a bakery produces 760 cupcakes during a 8 hour shift, what is the production rate of cupcakes per hour?
Answers
Answer:
The bakery makes 95 cupcakes per hour.
Step-by-step explanation:
To find the production rate per hour, we must divide.
In 8 hours the bakery makes 760 cupcakes
760/8 = 95
find the component form of v given its magnitude and the angle it makes with the positive x-axis. round your answer to four decimals. ‖v‖=8,θ=15°
Answers
Therefore, the component form of vector v is (7.7551, 2.0664) (rounded to four decimals).
To find the component form of a vector v given its magnitude and the angle it makes with the positive x-axis, we can use trigonometric functions to determine the x-component (v_x) and y-component (v_y) of the vector. In this case, we are given the magnitude of the vector ‖v‖ = 8 and the angle θ = 15°. The formulas for finding the components are:
v_x = ‖v‖ * cos(θ)
v_y = ‖v‖ * sin(θ)
Plugging in the given values, we have:
v_x = 8 * cos(15°)
v_y = 8 * sin(15°)
By evaluating these trigonometric functions, we can calculate the values:
v_x ≈ 8 * cos(15°) ≈ 7.7551
v_y ≈ 8 * sin(15°) ≈ 2.0664
These values represent the x-component and y-component of the vector v, respectively. So, the component form of vector v is approximately (7.7551, 2.0664) (rounded to four decimals).
To know more about component form of vector,
https://brainly.com/question/25138765
#SPJ11
A one-question survey is to be distributed to a random sample of 1500 adults in Ohio. The question asks if they support an increase in the state sales tax from 5% to 6%, with the additional revenue going to education. Let denote the proportion of adults in the sample who say they support the increase. Suppose that 40% of all adults in Ohio support the increase. What is the mean, , of the sampling distribution of ?
a.
40% ± 5%
b.
6%
c.
5%
d.
0.40
Answers
They support an increase in the state sales tax from 5% to 6%, with the additional revenue going to education. Let denote the proportion of adults in the sample who say they support the increase. Suppose that 40% of all adults in Ohio support the increase. the correct answer is (d) 0.40.
Mean is nothing but the average of the given set of values. It denotes the equal distribution of values for a given data
set. The mean, median and mode are the three commonly used measures of central tendency.
To calculate the mean, we need to add the total values given in a datasheet and divide the sum by the total number of
values.
The mean, μ, of the sampling distribution of p can be found using the formula
μ = p,
where p is the proportion of adults in the entire population who support the increase.
In this case, 40% of all adults in Ohio support the increase, so p = 0.40.
Therefore, the mean of the sampling distribution of p is:
μ = 0.40
So the correct answer is (d) 0.40.
for such more question on Mean
https://brainly.com/question/14532771
#SPJ11
The discount on a pack of socks is 15%. It is on sale for $17. What is the original price of the pack of socks?
Answers
Answer:
$19.55
Step-by-step explanation:
17*0.15=2.55
17+2.55=19.55
PLZZZZZZZZZZZZ PLZZZZZZZZZZZZ PLZZZZZZZZZZZZ PLZZZZZZZZZZZZ help

Answers
Answer:
a. option is the correct answer
Compute an actual dimension of a distance if the given
drawing measurement in the plan is 28 cm using a 1:60 m scale.
Answers
The actual dimension of the distance is approximately 0.0046667 cm.
To compute the actual dimension of a distance given a drawing measurement and a scale, you can use the following formula:
Actual Dimension = Drawing Measurement × Scale Factor
In this case, the given drawing measurement is 28 cm, and the scale is 1:60 m.
To calculate the scale factor, we need to convert the scale to the same unit as the drawing measurement. Since the drawing measurement is in centimeters (cm), we need to convert the scale from meters (m) to centimeters (cm).
1 meter = 100 centimeters
So, the scale factor is:
Scale Factor = 1:60 m = 1 cm : 60 cm = 1 : 6000 cm
Now we can calculate the actual dimension:
Actual Dimension = Drawing Measurement × Scale Factor
Actual Dimension = 28 cm × 1/6000
Actual Dimension = 28/6000 cm
Simplifying the fraction, we get:
Actual Dimension ≈ 0.0046667 cm
Therefore, the actual dimension of the distance is approximately 0.0046667 cm.
Learn more about distance from
https://brainly.com/question/17273444
#SPJ11
