PLS HELP Write an equation in slope-intercept form for the line that satisfies the following condition.
slope 5 and passes through (2, 28)

Answers
Answer:
y = 5x + 18
Step-by-step explanation:
The slope-intercept form is y = mx + b. Substitute 5 for m, 2 for x and 28 for y:
y = 28 = 5(2) + b, or
28 - 10 = b, or
18 = b
Then the desired equation is y = 5x + 18
Related Questions
A pollster wants to construct a 99.8% confidence interval for the proportion of adults who believe that economic conditions are getting better. Part 1 of 2 (a) A poll taken in July 2010 estimates this proportion to be 0.31. Using this estimate, what sample size is needed so that the confidence interval will have a margin of error of 0.02
Answers
99.8% confidence interval with a margin of error of 0.02, using the estimated proportion of 0.31 from the previous poll.
To find the sample size needed to construct a confidence interval for a proportion with a specified margin of error, we use the following formula:
n = (z^2 * p * q) / E^2
where:
n is the sample size
z is the z-score corresponding to the desired level of confidence (99.8% in this case)
p is the estimated proportion from the previous poll (0.31 in this case)
q = 1 - p
E is the desired margin of error (0.02 in this case)
First, we need to find the value of z for a 99.8% confidence level. Using a standard normal distribution table, we can find that the z-score for a 99.8% confidence level is approximately 2.967.
Substituting the given values into the formula, we have:
n = (2.967^2 * 0.31 * 0.69) / 0.02^2
n = 1202.19
Rounding up to the nearest whole number, we need a sample size of n = 1203 to construct a 99.8% confidence interval with a margin of error of 0.02, using the estimated proportion of 0.31 from the previous poll.
To learn more about poll visit:
https://brainly.com/question/28844387
#SPJ11
Barrybuysasurfboardonlinefor$66.Ifshippingandhandlingareanadditional10%oftheprice,howmuchshippingandhandlingwillBarrypay?
Answers
. Lila spent 72 minutes on the phone while routing 24 phone calls. In all, how many phone calls does Lila have to route to spend a total of 90 minutes on the phone? Solve using unit rates.
Answers
Answer:
To solve the problem using unit rates, we can first find Lila's rate of phone calls per minute, which is given by:
rate = number of phone calls / time spent on the phone
Using the values given in the problem, we get:
rate = 24 phone calls / 72 minutes
rate = 1/3 phone calls per minute
This means that Lila routes 1/3 phone call per minute.
To find how many phone calls Lila needs to route to spend a total of 90 minutes on the phone, we can use the same rate and the formula:
number of phone calls = rate x time
Substituting the values, we get:
number of phone calls = (1/3 phone calls per minute) x (90 minutes)
number of phone calls = 30 phone calls
Therefore, Lila needs to route a total of 30 phone calls to spend a total of 90 minutes on the phone.
Problem A fruit stand has to decide what to charge for their produce. They need \$10$10dollar sign, 10 for 444 apples and 444 oranges. They also need \$12$12dollar sign, 12 for 666 apples and 666 oranges. We put this information into a system of linear equations.
Answers
Answer:
4a + 4b = 10
6a + 6b = 12
Step-by-step explanation:
Putting the equation in a system of linear equation :
We donate, apples and oranges using any preffered letter or alphabet
Let :
Apples = a ; oranges = b
4 apples and 4 oranges equals $10
4a + 4b = 10
6 Apples and 6 oranges equals $12
6a + 6b = 12
Hence, the system of linear equation :
4a + 4b = 10
6a + 6b = 12
Answer:
No Solution
Step-by-step explanation:
It would require different amounts of dollars to fulfill eah equation.
Suppose a certain baseball diamond is a square 92 feet on a side. The pitching rubber is located 58.5 feet from home plate on a line joining home plate and second base. How far is it from the pitching rubber to first base?
Answers
A ---- B
| |
| |
D ---- C
Let A be home plate, B be first base, C be second base, and D be third base. The pitching rubber is located on a line connecting home plate and second base, 58.5 feet from home plate. Let's call the point where this line intersects the side AD "E". We want to find the distance from E to B.
Since the baseball diamond is a square, we know that AB = BC = CD = DA = 92 feet. We also know that AE + EC = AC = 92 feet. Using the Pythagorean theorem, we can find AE:
AE^2 + EC^2 = AC^2
AE^2 + (92 - AE)^2 = 92^2
Simplifying and solving for AE:
2AE^2 - 2(92)AE + 92^2 - 58.5^2 = 0
AE = (92 ± sqrt(4016.25)) / 2
AE ≈ 44.84 feet (we discard the negative solution since AE is a distance)
Finally, we can use the Pythagorean theorem again to find the distance from E to B:
EB^2 = AB^2 - AE^2
EB^2 = 92^2 - 44.84^2
EB ≈ 80.78 feet
Therefore, it is about 80.78 feet from the pitching rubber to first base.
during the first half of the year there were 54 students in the schools bicycling club. in the second half of the year the club had 68 members. find the percent of increase in club membership to the nearest whole percent
Answers
Answer:
To the nearest whole percent is 26%
Step-by-step explanation:
First half of the year = 54 students
Second half of the year = 68 members
find the percent of increase in club membership to the nearest whole percent ?
% increase in club membership = (new member - old member) / old member × 100
= (68 - 54) / 54 × 100
= 14 / 54 × 100
= 0.259 × 100
= 25.9 %
To the nearest whole percent is 26%
Assume that there are only two countries, the kingdoms of Florin and Guilder, each producing only two goods, really big blocks of cheese (X) and wagonloads of grain (Y) with the single input of labor under constant costs and perfect competition. Florin, the home country, has 3 million identical workers, each of whom can produce either 2 blocks of X or 6 wagonloads of Y per year. Guilder has 9.6 million workers, each of whom can produce either 1 block of X or 4 loads of Y per year. a. Putting X on the horizontal axis, draw and label the PPFs for both Florin and Guilder. Using indifference curves, show the consumption points (A and A*) assuming that each country devotes a third of its labor force to dairy production and two-thirds to wheat farming. Actual numbers (in millions) are required. b. Write the PPF equation for each country. c. Which has the absolute advantage in Y? Which has the comparative advantage in Y? d. Under free trade, which country would export which good, and why? This is called the Ricardian Theorem, by the way. e. Suppose both countries fully specialize. Show that moving to free trade from the previous points (A and A*) could lead to more total production of both X and Y. f. For each country, assuming that the price of Y relative to the price of X equals to 0.3, show the new Consumption Possibilities Frontier relative to the Production Possibilities Frontier.
Answers
In this scenario, Florin and Guilder are two countries producing two goods, cheese (X) and grain (Y), using labor as the only input. Florin has 3 million workers, each capable of producing 2 blocks of X or 6 wagonloads of Y per year. Guilder has 9.6 million workers, each capable of producing 1 block of X or 4 wagonloads of Y per year. By analyzing their production possibilities frontiers (PPFs) and comparing their labor productivity, we can determine their absolute and comparative advantages, and predict the outcome of free trade.
a) The PPFs for Florin and Guilder can be plotted with X on the horizontal axis and Y on the vertical axis. Given that each country allocates one-third of its labor force to dairy production and two-thirds to wheat farming, we can identify the consumption points (A and A*) where the indifference curves representing their preferences intersect with their PPFs.
b) The PPF equation for Florin can be written as X = 2L/3 and Y = 6L/3, where L represents the labor force. For Guilder, the PPF equation is X = L/9.6 and Y = 4L/9.6.
c) Guilder has the absolute advantage in producing Y as its workers are more productive in Y compared to Florin. However, Florin has the comparative advantage in producing Y because the opportunity cost of producing Y in terms of X is lower for Florin than Guilder.
d) Under free trade, Guilder would export Y and Florin would export X. This is based on the principle of comparative advantage, where each country specializes in producing the good for which it has a lower opportunity cost.
e) When both countries fully specialize and trade, there can be a higher total production of both X and Y compared to the previous consumption points (A and A*). By focusing on producing the goods in which they have a comparative advantage and engaging in trade, both countries can benefit from increased efficiency and resource allocation.
f) To show the new Consumption Possibilities Frontier (CPF) relative to the Production Possibilities Frontier (PPF), we can plot the new CPF by using the given relative price of Y to X (0.3) and connecting the points where each country consumes along the CPF based on their respective comparative advantage and terms of trade.
Learn more about productivity here:
https://brainly.com/question/31135471
#SPJ11
*Will mark brainliest*

Answers
Answer:
B
Step-by-step explanation:
solve the differential equation: d y d x = cos 2 ( x ) . the curve passes through point (0, 0).
Answers
To solve the differential equation dy/dx = cos^2(x) with the curve passing through the point (0, 0), we can integrate both sides of the equation. The solution to the differential equation is y = (1/2)x + (1/4)sin(2x).
The given differential equation is dy/dx = cos^2(x). To solve this equation, we integrate both sides with respect to x.
∫ dy = ∫ cos^2(x) dx.
The integral of cos^2(x) can be rewritten using the identity cos^2(x) = (1 + cos(2x))/2:
∫ dy = ∫ (1 + cos(2x))/2 dx.
Integrating each term separately:
y = (1/2)x + (1/2) ∫ cos(2x) dx.
The integral of cos(2x) is sin(2x)/2:
y = (1/2)x + (1/4)sin(2x) + C.
We can determine the value of the constant C using the initial condition that the curve passes through the point (0, 0). Substituting x = 0 and y = 0 into the equation:
0 = (1/2)(0) + (1/4)sin(2(0)) + C,
0 = 0 + 0 + C,
C = 0.
Therefore, the solution to the differential equation dy/dx = cos^2(x) with the curve passing through the point (0, 0) is y = (1/2)x + (1/4)sin(2x).
Learn more about differential equation here: brainly.com/question/25731911
#SPJ11
Add.
(6x³ + 3x² − 2) + (x³ - 5x² − 3)
Express the answer in standard form. (Please and thank you)
Answers
Answer:
\(\\\sf7x^3 - 2x^2 - 5\)
Step-by-step explanation:
\(\\\sf(6x^3 + 3x^2 - 2) + (x^3 - 5x^2 - 3)\)
Remove parenthesis.
6x^3 + 3x^2 - 2 + x^3 - 5x^2 - 3
Rearrange:
6x^3 + x^3 + 3x^2 - 5x^2 - 2 - 3
Combine like terms to get:
7x^3 - 2x^2 - 5----------------------------------------
More on adding polynomials: https://brainly.com/question/30791478
Hope this helps! :)
Answer:
7x³ - 2x² - 5
Step-by-step explanation:
(6x³ + 3x² - 2) + (x³ - 5x² - 3)
Remove the round brackets.
= 6x³ + 3x² - 2 + x³ - 5x² - 3
Put like terms together.
= 6x³ + x³ + 3x² - 5x² - 2 - 3
Do the operations.
= 7x³ - 2x² - 5
____________
hope this helps!
Find the length of the missing side. The triangle is not drawn to scale

Answers
Answer:10
Step-by-step explanation:Use the Pythagorean theorem a^2 + b^2 = c^2, a is 8 and b is 6 so now you have 8^2 + 6^2 = C^2 this simplifies to 64 + 36 = c^2 those 2 numbers add up to 100 so C^2 is 100 then to get C you take the square root of 100 which is 10
The missing side 10.
Option C is the correct answer.
What is the Pythagorean theorem?Pythagorean theorem states that for a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
We can apply this theorem only in a right triangle.
Example:
The hypotenuse side of a triangle with the two sides as 4 cm and 3 cm.
Hypotenuse side = √(4² + 3²) = √(16 + 9) = √25 = 5 cm
We have,
Applying the Pythagorean theorem.
c² = 6² + 8²
c² = 36 + 64
c² = 100
c = √100
c = 10
Thus,
The missing side is 10.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
for a one-tailed hypothesis test (upper tail), the p-value is computed to be .034. if the test is being conducted at the 5% level of significance, the null hypothesis group of answer choices could be rejected or not rejected depending on the sample mean could be rejected or not rejected depending on the sample size. is rejected. is not rejected.
Answers
For a one-tailed hypothesis test (upper tail), the p-value is computed to be .034. If the test is being conducted at the 5% level of significance, the null hypothesis C. is rejected
A one-tailed hypothesis test refers to a statistical test in which the alternative hypothesis is either greater than or less than the null hypothesis, but not both. Since the problem states that it is a one-tailed hypothesis test (upper tail), the alternative hypothesis, H1, will be a greater than or > sign. Hypothesis testing is the method of determining whether or not an assertion about a population parameter is consistent with sample data. A hypothesis test is conducted to assist in deciding between two competing hypotheses. One hypothesis is the null hypothesis (H0), which is a statement of the population parameter that is being tested.
In a hypothesis test, the null hypothesis is rejected if the test statistic falls in the rejection region. The test statistic, which measures the distance between a sample estimate and the null hypothesis, is used to assess whether or not the null hypothesis should be rejected. Reject the null hypothesis if the p-value is less than or equal to α. Since the p-value of 0.034 is less than the level of significance, α, of 0.05, the null hypothesis will be rejected, according to the question above. Therefore, option C is correct.
The Question was Incomplete, Find the full content below :
For a one-tailed hypothesis test (upper tail), the p-value is computed to be .034. If the test is being conducted at the 5% level of significance, the null hypothesis
a. could be rejected or not rejected depending on the sample size.
b. could be rejected or not rejected depending on the sample mean.
c. is rejected.
d. is not rejected.
Know more about the Hypothesis test here :
https://brainly.com/question/29576929
#SPJ11
Let V be a vector space, and T:V→V a linear transformation such that T(5v⃗ 1+3v⃗ 2)=−5v⃗ 1+5v⃗ 2 and T(3v⃗ 1+2v⃗ 2)=−5v⃗ 1+2v⃗ 2. Then
T(v⃗ 1)=
T(v⃗ 2)=
T(4v⃗ 1−4v⃗ 2)=
Answers
Let V be a vector space, and T:V→V a linear transformation then the value of T(v⃗ 1) = -v⃗ 1, T(v⃗ 2) = v⃗ 2 and T(4v⃗ 1 − 4v⃗ 2) = -4v⃗ 1 - 4v⃗ 2.
We can use the given information to find the value of T for various vectors in V and T:V→V a linear transformation such that T(5v⃗ 1+3v⃗ 2)=−5v⃗ 1+5v⃗ 2 and T(3v⃗ 1+2v⃗ 2)=−5v⃗ 1+2v⃗ 2.
For 5v⃗ 1 + 3v⃗ 2, we have:
T(5v⃗ 1+3v⃗ 2) = −5v⃗ 1+5v⃗ 2
5T(v⃗ 1) + 3T(v⃗ 2) = -5v⃗ 1 + 5v⃗ 2
Similarly, for 3v⃗ 1 + 2v⃗ 2, we have
T(3v⃗ 1+2v⃗ 2) = −5v⃗ 1+2v⃗ 2
3T(v⃗ 1) + 2T(v⃗ 2) = -5v⃗ 1 + 2v⃗ 2
Solving these equations for T(v⃗ 1) and T(v⃗ 2), we get
T(v⃗ 1) = -v⃗ 1
T(v⃗ 2) = v⃗ 2
Now, we can use these values to find T(4v⃗ 1 − 4v⃗ 2)
T(4v⃗ 1 − 4v⃗ 2) = 4T(v⃗ 1) - 4T(v⃗ 2)
= 4(-v⃗ 1) - 4(v⃗ 2)
= -4v⃗ 1 - 4v⃗ 2
Therefore, T(4v⃗ 1 − 4v⃗ 2) = -4v⃗ 1 - 4v⃗ 2.
To know more about linear transformation:
https://brainly.com/question/30514241
#SPJ4
11. What is the least common
70 ?
multiple of 30, 40, and
Answers
Answer:
i think 840 i searched it up
Step-by-step explanation:
a school has 2500 pupils. when 52 boys and 1/9 of the girls are absent, the number of the boys present is equal to the number of girls. how many does doe he school have
Answers
a school has 2500 pupils. when 52 boys and 1/9 of the girls are absent, the number of the boys present is equal to the number of girls. how many pupils does the school have ?
Solution :Let the number of boys be x
Data :
Total pupils = 2500
Absent no. of boys and girls = 52 and 1/9
Now,
First of all we need to get the number of girls then add it with the no. of boys absent and then subtract the whole from 2500 to get the required answer.Remaining no of pupils = 2500 - 52 ➝ 2448
Hence, the no. of girls absent = 1/9 of 2448 ➝ 272
Therefore,
Total no. of pupils absent = 52 + 272 ➝ 324
No. of pupils present = 2500 - 324 ➝ 2176
Henceforth, 2176 pupils are present
Point B lies on line AC, as shown on the coordinate grid below. Given that AD = 2
units, DB = 3 units, and BE = 4 units, how many units is EC?

Answers
The side EC is 6 units.
What is Triangle?A triangle is a three-sided polygon that consists of three edges and three vertices.
Given that Point B lies on line AC, as shown on the coordinate grid below.
AD = 2 units,
DB = 3 units, and
BE = 4 units
We need to find EC.
As we observe the triangle ADB is similar to BEC.
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion .
AD is corresponding side of BE and DB is corresponding side of EC.
As the sides are proportional
2/3=4/x
2x=12
x=6
Hence, the side EC is 6 units.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ1
The table shows the amount of money Tyler earns for mowing lawns. Is the
relationship a proportional relationship? Complete the explanation.

Answers
Answer:
The constant of variation 'k' is NOT constant.
Therefore, we conclude that Taylor did not charge a constant rate. The rates are not equal because his rate changed.
Step-by-step explanation:
Given the table
Number of Lawns 1 2 3 4
Amount Earned ($) 16 32 54 72
We know that when y varies directly with x, we get the equation
y ∝ x
y = kx
k = y/x
where 'k' is called the constant of proportionality.
In our case, the 'Amount earned ($) ' is represented by 'y', and the 'Number of Lawns' is represented by 'x'.
Let us check the constant of proportionality using the equation
k = y/x
k = 16/1 = 16
k = 32/2 = 16
k = 54/3 = 18
k = 72/4 = 18
It is clear that that the constant of variation 'k' is NOT constant.
Therefore, we conclude that Taylor did not charge a constant rate. The rates are not equal because his rate changed.
simplify (2xyz^2)^5.
Answers
Answer:
4x^5y^5z^7
Step-by-step explanation:
4x^5y^5z^7
Answer:
\((2xyz^2)^5\)
This equation shows us that the whole thing in the parenthesis need to be multiplied by 5 times.
The result:
\(=32x^5y^5z^{10}\)
(\(\left(a^b\right)^c=a^{bc}\) this is how I got the exponent 10 for z)
Write the repeating decimal 4.1363636… as a fraction.
Answers
Answer:4¹⁵/110
Step-by-step explanation:
Take x to be the number
X=4.13636363
Since the repeating numbers are 2 you multiply the number by 100
100x =413.636363
When we minus 413.6363 and 4.136363 we will get a decimal
We multiply the value for x by 1000 we get 4136.3636
And when we minus 4136.3636 by the values of 1x and 100x we will still get a decimal
We multiply the value of x by 10000 we will get 41363.6363 when we divide it by the values of 1x we will get a decimal but when we divide it by the value of 100x we will not get a decimal
Then we minus them
10000×-100×=9900x
41363.6363-413.6363=40950
9900x=40950
Divide both sides by 9900
9900x÷9900=40950÷9900
X=4¹⁵/110
please help if possible, there is a graph, and then an A and B question, please answer both.
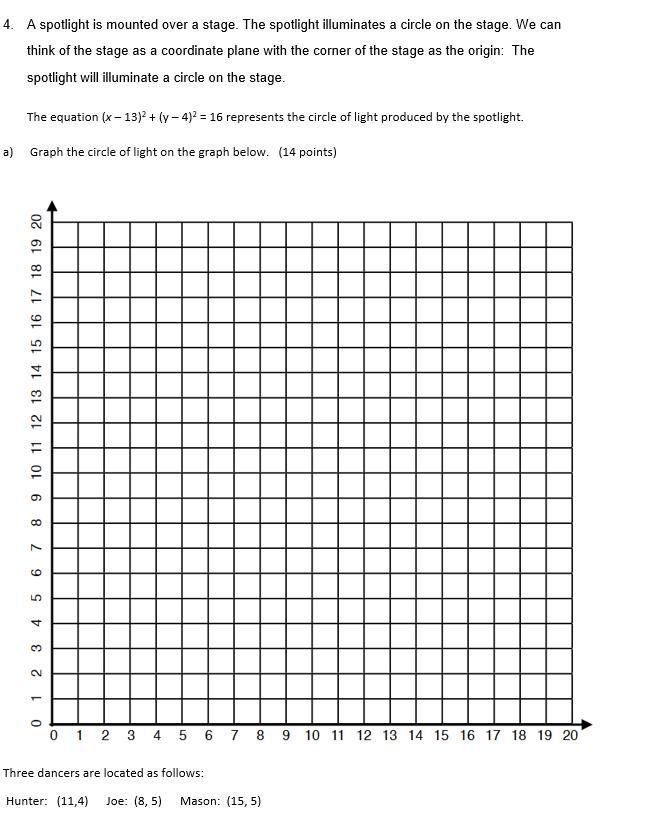

Answers
Part A
we have the equation
(x-13)^2+(y-4)^2=16
Rewrite as
(x-13)^2+(y-4)^2=4^2
so
The center of the circle is the point (13,4)
The radius of the circle is 4 units
using a graphing tool
Part B
Remember that
If an ordered pair lies on the circle, then the ordered pair must satisfy the equation of the circle
so
Verify each ordered pair
Hunter (11,4)
For x=11 and y=4
substitute in the equation of the circle
\(\begin{gathered} \left(11-13\right)^2+\left(4-4\right)^2=16 \\ -2^2+0^2=16 \\ 4=16 \end{gathered}\)Is not true
so
Hunter is not in the spotlight
Joe (8,5)
x=8 and y=5
\(\begin{gathered} (8-13)^2+(5-4)^2=16 \\ -5^2+1=16 \\ 26=16 \end{gathered}\)Is not true
so
Joe is not in the spotlight
Mason (15,5)
x=15 and y=5
\(\begin{gathered} (15-13)^2+(5-4)^2=16 \\ 2^2+1^2=16 \\ 5=16 \end{gathered}\)Is not true
Mason is not in the spotlight

Factor completely 18x2 − 21x −15. 3(2x 1)(3x − 5) 3(2x − 5)(3x 1) 3(2x − 1)(3x 5) 3(6x 1)(x − 5).
Answers
The factor of the \(18x^{2} -21x-15\) will be 3(3x-5)(2x+1).
What will be the factor of \(18x^{2} -21x-15\) ?Given quadratic equation is \(18x^{2} -21x-15\)
By taking 3 common from whole of the equation it becomes.
\(3(6x^{2} -7x-5)\)
now by factorization equation will be.
\(3(6x^{2} -10x+3x-5)\)
3[(2x(3x-5)+1(3x-5)]
Taking (3x-5) common from whole equation it will become
3(3x-5)(2x+1).
Hence the factor of the \(18x^{2} -21x-15\) will be 3(3x-5)(2x+1).
To know more about factorization follow.
https://brainly.com/question/25829061
#2) Salim bought 32 feet of window trim at a hardware store. The trim cost $1.75 per foot. Salim used a 20\% coupon to purchase the window trim. A sales tax of 9.5% was applied to the total purchase. How much does Salim end up paying for the window trim?
Answers
Answer: $49.056
Step-by-step explanation:
Salim bought 32 feet of window trim at a hardware store and the trim cost $1.75 per foot. The total cost will then be:
= 32 × $1.75
= $56
She used a 20% coupon to purchase the window trim. The amount she will pay will be:
= $56 - (20% × $56)
= $56 - (0.2 × $56)
= $56 - $11.2
= $44.8
A sales tax of 9.5% was then applied to the total purchase. The amount Salim will end up paying will be:
= $44.8 + (9.5% × $44.8)
= $44.8 + (0.095 × $44.8)
= $44.8 + $4.256
= $49.056
A wheel on tractor has a 30-inch diameter How many full revolutions does the wheel make if the tractor travels 7 miles? (Round your answer down to the nearest whole number.)
Answers
The number of revolution the wheel makes in 7 miles is 4706 revolutions
How to find the number of full revolutions the wheel makes?Since the wheel is a circle, its circumference is travelled in 1 revolution.
So, circumference C = πd where d = diameter of wheel = 30 in
So, C = πd
= π × 30 in
= 30π in
= 94.25 in
Now, we need to find the number of revolutions the wheel makes when the tractor travels D = 7 miles.
Since 1 mile = 63360 in,
Converting miles to inches, we have D = 7 miles
= 7 × 1 mile
= 7 × 63360 in
= 443520 in
So, the number of revolution the wheel makes in 7 miles is N = D/C
= 443520 in/94.25
= 4705.89
≅ 4706 to the nearest whole number
So, the number of revolution the wheel makes in 7 miles is 4706 revolutions
Learn more about number of revolutions of wheel here:
https://brainly.com/question/11029250
#SPJ1
14. Write the ratio 15:5 with second term 1.
a. 10:1
b. 3:1
C.
11:1
d. 5:1
Answers
Answer:
your answer would be b
Step-by-step explanation:
if you divide each side by 5 you get
15/5:5/5
3:1
hope this helps! have a nice day!
5/1 = 1
15/5= 3
So 3:1
The population of a school is 800 and is decreasing at a rate
of 2% per year; 4 years
Answers
Answer:
i think the answer is 738
Help me with the answer?? Answer please answer to answer ??

Answers
We want to find the value of x, which is the hypotenuse of the triangle on the image.
We will see that the value of x is 5.77 units.
How to find the value of x?On the figure we can see a right triangle, we want to find the value of x, which is the hypotenuse of this triangle.
To do so, we can use the trigonometric relation:
cos(θ) = (adjacent cathetus)/(hypotenuse)
Where θ is an internal angle of the triangle, and the adjacent cathetus is the cathetus that forms the angle.
Here we can use θ = 30°, and the adjacent cathetus is the one that has a measure of 5 units, then the value of x is given by the equation:
cos(30°) = 5/x
Solving that for x we will get:
x = 5/cos(30°) = 5.77
The hypotenuse measures 5.77 units.
Learn more about right triangles:
https://brainly.com/question/2217700
#SPJ1
(will give BRAINLIEST)The formula for the perimeter of a rectangle Is P = 2(1+w). Part A. Rewrite the formula for the perimeter of a rectangle in terms of the width w. In your final answer, Include all of
your work
Part B. In two or more complete sentences, describe the process you followed while Isolating the varlable w In the
equation P=2(1+w).
Answers
B. First you need to divide both sides by 2 to get rid of the 2 on the side of the w. Then you need to take 1 away from both sides.
Whatever you do to one side, you must do to the other.
Hope this helps x
In a collection of 50 cards, Sal has some valuable and some regular cards. He has 16 more valuable cards than regular cards. How many of each kind of card does Sal have? Explain the situation using an equation and solve.
Answers
Answer: 17 Regular, 33 Valuable
Step-by-step explanation:
Given
Sal has 50 cards
He has 16 more valuable card than regular cards
Suppose he has x regular cards
So, valuable cards are x+16
Their sum must be 50
\(\Rightarrow x+x+16=50\\\Rightarrow 2x=50-16\\\Rightarrow 2x=34\\\Rightarrow x=17\)
Therefore, he has 17 regular cards and 33 valuable cards
Coffee is draining from a conical filter with height and diameter both
15
cm, into a cylindrical coffee pot with diameter
15
cm. The rate at which coffee drains from the filter into the pot is
100
cc/min. The rate in cm/min at which the level in the pot is rising at the instant when the coffee in the pot is
10
cm, is
Answers
The rate at which the level in the coffee pot is rising, when the coffee in the pot is 10 cm, is approximately 20 cm/min. To find the rate at which the level in the coffee pot is rising, we can consider the volume of coffee that is draining from the filter into the pot.
The rate at which the coffee drains from the filter is given as 100 cc/min. Since the filter and pot have the same diameter, the area of the base of the filter and pot is the same.
The volume of a cone is given by the formula V = (1/3)πr²h, where r is the radius and h is the height. The volume of coffee draining per minute can be calculated using the height of the cone, which is 15 cm. Substituting the values, we have V = (1/3)π(7.5²)(15) cc/min.
When the coffee in the pot is 10 cm, the volume of coffee in the pot is given by V =π(7.5²)(10) cc. Now, we can differentiate the volume with respect to time to find the rate at which the level is rising.
dV/dt = π(7.5²)(dh/dt)
100 cc/min = π(7.5²)(dh/dt)
Simplifying the equation, we can find that dh/dt is approximately 20 cm/min. Therefore, the rate at which the level in the pot is rising at the instant when the coffee in the pot is 10 cm is approximately 20 cm/min.
Learn more about diameter here: https://brainly.com/question/31445584
#SPJ11
a college's soccer team will play 18 games next fall. each game can result in one of 3 outcomes: a win, a loss, or a tie. find the total possible number of outcomes for the season record.
Answers
The total possible number of outcomes for the season record is 3¹⁸, or 387,420,489. This is because there are three possible outcomes for each of the 18 games: win, loss, or tie.
To find the total number of outcomes, you can use the fundamental counting principle, which states that the total number of outcomes is equal to the product of the number of outcomes for each event. For example, if you flip a coin twice, there are two possible outcomes for each flip: heads or tails. Using the fundamental counting principle, you can find the total number of outcomes by multiplying the number of outcomes for each event:2 x 2 = 4So there are four possible outcomes for flipping a coin twice: heads-heads, heads-tails, tails-heads, or tails-tails. Using the same logic, you can find the total number of outcomes for the soccer team's season record by multiplying the number of outcomes for each game:3 x 3 x 3 x ... (18 times)= 3¹⁸= 387,420,489So there are 387,420,489 possible outcomes for the soccer team's season record.
To know more about counting principle refer here:
https://brainly.com/question/29079509
#SPJ11