Answers
Answer: b I think
Step-by-step explanation:
Related Questions
Find an equation of the tangent plane to the surface 3z = xe^xy + ye^x at the point 6,0,2).
Use Lagrange multipliers to find the minimum value of the function
f(x,y,z) = x^2-4x+y^2-6y+z^2-2z+5, subject to the constraint x+y+z=3.
Answers
The equation of the tangent plane to the surface 3z = xe^xy + ye^x at the point (6, 0, 2) is x + 37y + 3z - 12 = 0.
To find the equation of the tangent plane to the surface 3z = xe^xy + ye^x at the point (6, 0, 2), we will follow these steps:
Find the partial derivatives of the surface equation with respect to x, y, and z.
Partial derivative with respect to x:
∂(3z)/∂x = e^xy + xye^xy
Partial derivative with respect to y:
∂(3z)/∂y = x^2e^xy + e^xy
Partial derivative with respect to z:
∂(3z)/∂z = 3
Evaluate the partial derivatives at the point (6, 0, 2).
∂(3z)/∂x = e^(60) + 60e^(60) = 1
∂(3z)/∂y = (6^2)e^(60) + e^(60) = 37
∂(3z)/∂z = 3
The equation of the tangent plane can be written as:
∂(3z)/∂x(x - 6) + ∂(3z)/∂y(y - 0) + ∂(3z)/∂z(z - 2) = 0
Substituting the evaluated partial derivatives:
1(x - 6) + 37(y - 0) + 3(z - 2) = 0
x - 6 + 37y + 3z - 6 = 0
x + 37y + 3z - 12 = 0
Therefore, the equation of the tangent plane to the surface 3z = xe^xy + ye^x at the point (6, 0, 2) is x + 37y + 3z - 12 = 0.
Now, let's use Lagrange multipliers to find the minimum value of the function f(x, y, z) = x^2 - 4x + y^2 - 6y + z^2 - 2z + 5, subject to the constraint x + y + z = 3.
Define the Lagrangian function L(x, y, z, λ) as:
L(x, y, z, λ) = f(x, y, z) - λ(g(x, y, z) - c)
Where g(x, y, z) is the constraint function (x + y + z) and c is the constant value (3).
L(x, y, z, λ) = x^2 - 4x + y^2 - 6y + z^2 - 2z + 5 - λ(x + y + z - 3)
Compute the partial derivatives of L with respect to x, y, z, and λ.
∂L/∂x = 2x - 4 - λ
∂L/∂y = 2y - 6 - λ
∂L/∂z = 2z - 2 - λ
∂L/∂λ = -(x + y + z - 3)
Set the partial derivatives equal to zero and solve the system of equations.
2x - 4 - λ = 0 ...(1)
2y - 6 - λ = 0 ...(2)
2z - 2 - λ = 0 ...(3)
x + y + z - 3 = 0
To learn more about equation, refer below:
https://brainly.com/question/29657983
#SPJ11
PLEASE HELP ASAP show work pls will mark the brainliest.

Answers
The value of x as shown in the diagram is 2.
What is a tangent to a circle?
Tangent to a circle is the line that touches the circle at only one point.
Note: Tangent drawn from the same external points are equal.
To calculate the value of x, we use the above fact.
From the diagram,
Tangent /JK/ =Tangent /JM/ (Both from the smae external points)................. Equation 1Given:
/JK/ = 5x-4/JM/ = 2x+2Substitute into equation 1 and solve for x
5x-4 = 2x+25x-2x = 2+43x = 6x = 6/3x = 2Hence, x = 2.
Learn more about tangent here: https://brainly.com/question/30085302
#SPJ1
the temperature at the point (x, y) on a metal plate is t(x, y) = x x2 y2 . find the direction of greatest increase in heat from the point (2, 5).
Answers
The direction of greatest increase in heat from the point (2, 5) on the metal plate described by the temperature function t(x, y) = x^3 y^2 is along the positive x-axis. This means that the temperature increases the most as we move in the direction of increasing x-coordinate.
To find the direction of greatest increase in heat from the point (2, 5) on the metal plate, we need to calculate the gradient vector of the temperature function t(x, y) = x^3 y^2. The gradient vector represents the direction of the steepest increase in a scalar function.
Let's calculate the partial derivatives of t(x, y) with respect to x and y:
∂t/∂x = 3x^2 y^2
∂t/∂y = 2x^3 y
Now, evaluate the partial derivatives at the given point (2, 5):
∂t/∂x = 3(2)^2 (5)^2 = 300
∂t/∂y = 2(2)^3 (5) = 80
The gradient vector (∇t) at (2, 5) is given by (∂t/∂x, ∂t/∂y) = (300, 80). The direction of the gradient vector indicates the direction of the steepest increase in heat. Since the x-component (300) is larger than the y-component (80), the direction of greatest increase in heat is along the positive x-axis.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
a recent article claims that the state of illinois has low tuition rates for its colleges and universities. cate decides to research the cost of tuition for different colleges in illinois. the average tuition in illinois is $28,950 with a standard deviation of $3,470. which type of inference test should cate use? a.) chi-squared test for goodness-of-fit b.) two-way anova c.) one-sample z-test d.) one-sample t-test
Answers
The correct option c.) one-sample z-test, for the inference test used by the Cate.
What is defined as the one-sample z-test?When determining if a difference between a sample's mean and a population's mean is substantial sufficiently to be statistically significant—that is, because unless it is unlikely to have taken place by chance—we utilize the one-sample z-test. The test is typically used with reasonably large samples (N > 30) or whenever the population variance is known because it is thought to be robust for breaches of normal distribution; otherwise, you can think about using the t-test.As stated in the assertion
In Illinois, the average cost of tuition is $28,950, with a $3,470 standard deviation.This is a one-sample z-test, assuming we have a sizable sample, as we are comparing the mean of one group to an assumed value.As a result, cate uses one sample Z Test.
To know more about the one-sample z-test, here
https://brainly.com/question/17144617
#SPJ4
what is the probablilty that the sample mean contents of the 10 bottles
Answers
The probability of the sample mean contents of the 10 bottles will depend on the distribution of the contents in the population, the sample size, and the sample mean.
The probability of the sample mean contents of the 10 bottles will depend on the distribution of the contents in the population from which the sample is drawn. If the distribution is normal, then the probability of the sample mean can be calculated using the formula:
P(x) = (1 / √(2πσ^2)) * e^(-(x-μ)^2 / (2σ^2))
Where μ is the population mean, σ is the population standard deviation, and x is the sample mean. The probability of the sample mean will be the area under the normal curve between the sample mean and the population mean.
If the distribution is not normal, then the probability of the sample mean can be calculated using the central limit theorem, which states that the distribution of sample means approaches a normal distribution as the sample size increases. In this case, the probability of the sample mean can be calculated using the formula for the normal distribution, with the sample mean as the mean and the standard error of the mean as the standard deviation.
Learn more about probability:https://brainly.com/question/25870256
#SPJ11
what absolute value inequality can be written to determine the range of acceptable bead lengths, and what is this range of lengths? enter your answers in decimal form by filling in the boxes. absolute value inequality:
Answers
The absolute value inequality to determine the range of acceptable bead lengths is |B - 4.3| ≤ 0.2, and the range of acceptable lengths is 4.1 ≤ B ≤ 4.5 centimeters.
Given that the target length (L) of the ceramic bead is 4.3 centimeters with an acceptable allowance (T) of 0.2 centimeters, we can write the absolute value inequality as follows:
|B - 4.3| ≤ 0.2
This inequality states that the absolute difference between the bead length (B) and the target length (4.3) must be less than or equal to 0.2.
To determine the range of acceptable bead lengths, we can solve this inequality. Let's consider two cases:
Case 1: B - 4.3 ≤ 0.2
Solving for B:
B ≤ 4.5
Case 2: -(B - 4.3) ≤ 0.2
Solving for B:
-B + 4.3 ≤ 0.2
4.3 - 0.2 ≤ B
B ≥ 4.1
Combining both cases, the range of acceptable bead lengths is:
4.1 ≤ B ≤ 4.5
Therefore, the range of acceptable bead lengths is from 4.1 centimeters to 4.5 centimeters.
To know more about inequality, refer here:
https://brainly.com/question/32844662
#SPJ4
Complete Question:
The length of a manufactured ceramic bead is 4.3 centimeters with an acceptable allowance of 0.2 centimeters. Beads that are too big or too small are discarded.
What absolute value inequality can be written to determine the range of acceptable bead lengths, and what is this range of lengths?
Not sure what the radius is or what the answer is, help would be appreciated.

Answers
Step-by-step explanation:
According to angles of intersecting chords theorem ( angle S is also 117):
117 = 1/2 (208 + 2x-4)
so x = 15
then 2x-4 = 26 degrees
I ordered some books online for myself and friends.
Each book costs $13 and the store charges a one-time shipping fee of $ 20
Write an expression for the cost of buying nn books.
Answers
The expression for the cost of buying n book will be 20 + 13n.
How to illustrate the expression?Expression simply refers to the mathematical statements which have at least two terms which are related by an operator and contain either numbers, variables, or both. Addition, subtraction, multiplication, and division are all possible mathematical operations.
It is a finite collection of symbols that are well-formed in accordance with context-dependent principles. Numbers, variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.
In this case, the person some books online for myself and friends and each book costs $13 and the store charges a one-time shipping fee of $20.
The expression for the cost of buying n books is:
= 20 + (13 × n)
= 20 + 13n
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
Solve for x: 5(x-3)=5
Answers
Answer:
x=4
Step-by-step explanation:
5(x−3)=5
Step 1: Simplify both sides of the equation.
5(x−3)=5
(5)(x)+(5)(−3)=5(Distribute)
5x+−15=5
5x−15=5
Step 2: Add 15 to both sides.
5x−15+15=5+15
5x=20
Step 3: Divide both sides by 5.
5x / 5 = 20 / 5
x=4
I know this answer
evaluate lim x tends to 0 (9^x+(9^-x) -2)/x^2
Answers
Answer:
= (ln(9))^2 = 4(ln(3))^2 = 4.8278
Step-by-step explanation:
Using L'hopital Theorem
Defrentiante the numerator and denominator twice each by its self.
like in here :
http://ar.symbolab.com/solver/limit-calculator/%5Clim_%7Bx%5Cto0%7D%5Cleft(%5Cfrac%7B9%5E%7Bx%7D%2B9%5E%7B-x%7D-2%7D%7Bx%5E%7B2%7D%7D%5Cright)
for any other limit calculation use this : http://ar.symbolab.com/solver/limit-calculator/
Date
9. Mike bought a set of golf clubs that cost k dollars. He signed an installment agreement requiring
a 5% down payment and monthly payments of g dollars for 1 1/2 years.
a. Express his down payment algebraically.
b. How many monthly payments must Mike make?
c. Write expressions for the total amount of the monthly payments and the finance charge.
Answers
The total amount of the monthly payments and the finance charge is 144.
What is instalment?Instalment is one of the regular payments that anyone can make for anything until you have fully paid that full amount.
Using the appropriate interest relation, the solution to the problems posed are :
Down payment = 0.05k
144 monthly payments
Total monthly payment made = 144g
Down payment :
5% of total cost
Total cost = k
5% × k = 0.05k
B.)
Number of monthly payments :
Number of months per year = 12
Number of years = 12
Number of monthly payments = 12 × 12 = 144
C.)
Total charge :
Monthly payment = $g
Number of monthly payments × amount paid
g × 144 = 144g
To know more about instalment click-
https://brainly.com/question/16032019
#SPJ1
Angles are created when lines a and b are cut by a transversal, t. These angles are labeled in the diagram.
Select the claim that is true about lines a and b for all cases.
A
If lines a and b are cut by a transversal, t, such that m∠1=m∠5, m∠2=m∠6, m∠3=m∠7, and m∠4=m∠8, then the lines must be parallel.
B
If lines a and b are cut by a transversal, t, such that m∠1+m∠5=180°, m∠2+m∠6=180°, m∠3+m∠7=180°, and m∠4+m∠8=180°, then the lines must be parallel.
C
If lines a and b are cut by a transversal, t, such that m∠1=m∠5, m∠2=m∠6, m∠3=m∠7, and m∠4=m∠8, then the lines must be perpendicular.
D
If lines a and b are cut by a transversal, t, such that m∠1+m∠5=90°, m∠2+m∠6=90°, m∠3+m∠7=90°, and m∠4+m∠8=90°, then the lines must be perpendicular.
PLEASE ANSWER FAST
Answers
Answer:
<7= 101
<8= 101
Hence, <1= 101, <2=79, <3= 101, <4= 101, <5= 79, <6= 79, <7= 101, and <8= 101
Step-by-step explanation:
3x + 19 = 5x - 29 ( opposite angles)
2x = 48
x = 24
Hence, the value N = 2y
< 2 = 3x + 7 ( Verticaly opposite angles).
<2 = 3 (24) + 7
<2 = 79
<1 + <2 = 180
<1 = 180 - <2 = 180 - 79 = 101
<1 = 101
<1 = 3 ( Opposite angle )
<3 = 101
<5 = 3x + 7 ( Adjacent angles )
<5 = 79
<4 + <5 = 180
<4 = 101
<6 = <5 ( Verticaly opposite angles )
<6 = 79
<7 = <4 ( Adjacent Angles )
< 8 = 4x + 5
<7 = 101
<8 = 101
Hence, <1 = 101, <2 = 79, <3 = 101, <4 = 101, <5 = 79, <6 = 79, <7 = 101, <8 = 101
When finding the multiples of 2, how can I figure out the 6th term?
Answers
Answer:
2×1=2
2×2=4
2×3=6
2×4=8
2×5=10
2×6=12 ==> Answer
¿cuanto es 150% en una fracción?
no se como aser esto. alguien me ayuda?
que difícil , explica bien soy algo ruda mejor dicho muy ruda en eso
Answers
Answer:
3/2 o 1 entero 1/2
Step-by-step explanation:
150% es igual a 150 sobre 100= 150/100
(% este simbolo significa que el numero será divido por 100)
simplificas y te va a salir 3/2
Is the question ''how many cars were sold each day this month'' statistical or not?
Answers
Help
Will
Give
Brainlist
M
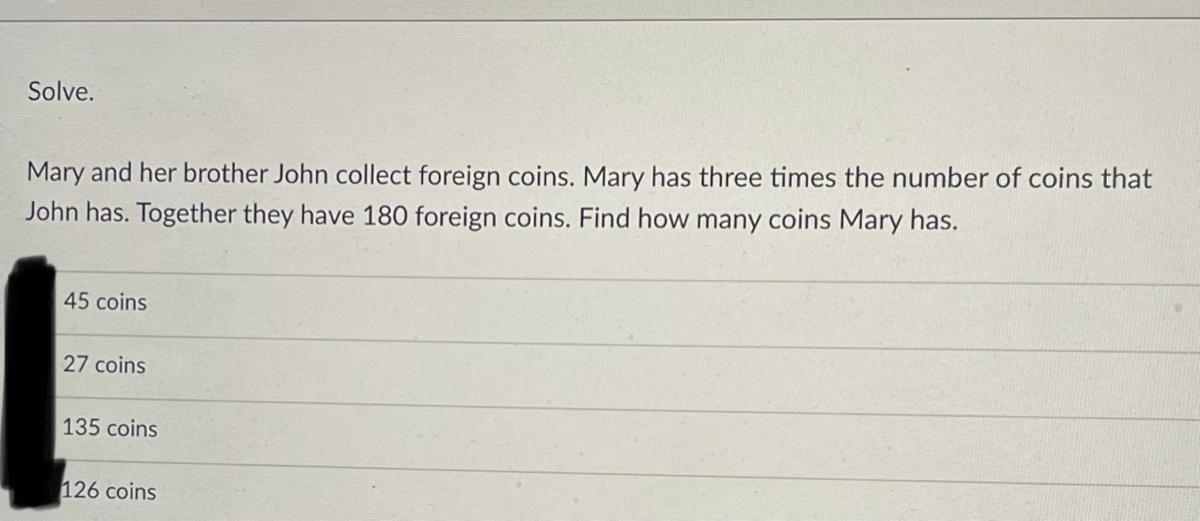
Answers
Answer:
mary has 135 coins.
Step-by-step explanation:
let the coins that john has be x
and coin mary than = 3x
according to the question equation is
x + 3x = 180
4x = 180
x = 180 / 4
x = 45
coins mary has = 3x
=3*45
=135
Sarah bakes 420 cookies. She bakes only chocolate, raisings, toffee and plain cookies. 2 /7 of the cookies are chocolate cookies.
35% of the cookies are raising cookies.
The ratio of the number of toffee cookies to plain cookies is 4: 5. work out the number of toffee cookies.
Answers
The number of toffee cookies Sarah baked is:
4x = 4(17) = 68
If 2/7 of the cookies are chocolate cookies then the number of chocolate cookies Sarah baked is:
2/7 x 420 = 120
If 35% of the cookies are raisin cookies then the number of raisin cookies Sarah baked is:
35/100 x 420 = 147
Let the number of toffee cookies be 4x and the number of plain cookies be 5x x is a constant.
The total number of cookies is the sum of the number of chocolate raisin toffee and plain cookies:
Total number of cookies = Number of chocolate cookies + Number of raisin cookies + Number of toffee cookies + Number of plain cookies
Substituting the values we know:
420 = 120 + 147 + 4x + 5x
Simplifying and solving for x:
420 = 267 + 9x
9x = 153
x = 17
The number of toffee cookies Sarah baked is:
4x = 4(17) = 68
For similar questions on cookies
https://brainly.com/question/29104131
#SPJ11
Use Inverse operations to solve the expression. Enter your answer in simplest form. y 1 =8 16

Answers
(-8) y/(-8) = (-8) 1/16
y = -8/16
and simplified:
y = -1/2
Find an equation in point-slope form for the line having the slope m =1/3 and containing the point (-3,- 6).
Answers

Suppose that (x,square root7/3) is a point in quadrant 1 find x
Answers
Value of x = √2/3, and co-ordinate of point will be (√2/3 , \(\sqrt{7} /3\) )
Unit circle:
Circle having radius 1 unit is called unit circle.
Let us consider,
co-ordinate of point is (x , \(\sqrt{7} /3\) )
as the above point is lying on the first quadrant and on unit circle.
for the unit circle,
\(x^{2} + y^{2} =1\) center of circle (0,0)
parametric form of equation
x = cosθ and y=sinθ
so any point on the unit circle will be,
(x, y) = ( cosθ ,sinθ )
for,
(x , \(\sqrt{7} /3\) )
y = \(\sqrt{7} /3\)
sinθ = \(\sqrt{7} /3\)
x = cosθ
= ± √(1 - sin^2 θ)
= ± √(1 - 7/9)
= ± √((9- 7)/9)
= ± √(2/9)
= ± √2/3
but we can not take the negative value, because co-ordinate point is lying in the first quadrant.
so,
x = √2/3
thus ,
co-ordinate of point will be
(x, y) = (√2/3 , \(\sqrt{7} /3\) )
To learn more about unit circle visit : https://brainly.com/question/23519482
#SPJ9
(-10,-7) (-8,1) find the distance between two points
Answers
Answer: \(\sqrt{68}\) units.
Step-by-step explanation:
The distance between points (a, b) and (c, d) is given by :_
\(D=\sqrt{(d-b)^2+(c-a)^2}\)
Given points : (-10,-7) (-8,1)
Distance between points (-10,-7) and (-8,1) = \(\sqrt{(1-(-7))^2+(-8-(-10))^2}\)
\(=\sqrt{(1+7)^2+(-8+10)^2}\\\\=\sqrt{8^2+2^2}\\\\=\sqrt{64+4}\\\\=\sqrt{68}\)
Hence, distance between given points = \(\sqrt{68}\) units.
hellllllllpppppp please i need it

Answers
Send a better cropped
photo
Suppose you are a quality controller in a manufacturing company and want to determine whether there is any difference in the mean measurements of shaft ...
Answers
As a quality controller in a manufacturing company, I would conduct a hypothesis test to determine if there is a significant difference in the mean measurements of shaft diameters between two groups.
To conduct the hypothesis test, I would collect a sample of shaft measurements from each group and calculate the sample means. Then, I would perform a statistical test, such as a two-sample t-test, to compare the means of the two groups. The null hypothesis (H0) would state that there is no difference in the mean shaft measurements between the groups, while the alternative hypothesis (Ha) would suggest that there is a significant difference.
The test would provide a p-value, which indicates the probability of observing a difference in the means as extreme as the one obtained in the sample, assuming that the null hypothesis is true. If the p-value is below a predetermined significance level (e.g., 0.05), we would reject the null hypothesis and conclude that there is a significant difference in the mean measurements of the shaft diameters between the two groups. This would indicate the presence of a systematic variation or discrepancy in the manufacturing process that needs to be addressed to ensure consistent quality in the shaft production.
Learn more about probability here: brainly.com/question/32117953
#SPJ11
the deseasonalized sales for this period when the actual sales are 2,763.00 units and the seasonal index for this period is 0.84?
Answers
The deseasonalized sales for this period, when the actual sales are 2,763.00 units and the seasonal index for this period is 0.84, are 3,289.29 units.
To find the deseasonalized sales for a given period, we need to divide the actual sales by the seasonal index for that period. This will give us the sales that would have occurred if there were no seasonal fluctuations.
In this case, the actual sales are 2,763.00 units and the seasonal index is 0.84. So, we can use the following formula to find the deseasonalized sales:
Deseasonalized sales = Actual sales / Seasonal index
Deseasonalized sales = 2,763.00 / 0.84
Deseasonalized sales = 3,289.29 units
Therefore, the deseasonalized sales for this period are 3,289.29 units.
You can learn more about deseasonalized sales at
https://brainly.com/question/29846523
#SPJ11
Complete the steps to calculate the density of the steel. calculate the volume of the prism. recall that the area of a hexagon is one-half times the apothem times the perimeter. v = cm3 calculate the volume of the cylinder. round to the nearest hundredth. v = cm3 find the volume of the composite figure. v = cm3 calculate the density by dividing the mass by the volume. d = g/cm3
Answers
Answer:
1. 0.45
2. 0.06
3. 0.39
4. 7.77
Step-by-step explanation:
causeeeeeeee
Which of the following shows the prime factorization of 72 using exponential notation?2.6²8.923 . 322².32O
Answers
Remember that any natural number can be written as a product of prime numbers. Prime numbers are those numbers that are only divisible by one and themselves.
In the case of 72:
\(\begin{gathered} 72=9\cdot8 \\ \Rightarrow72=(3\cdot3)\cdot(2\cdot2\cdot2) \\ \Rightarrow72=2^3\cdot3^2 \end{gathered}\)Therefore, the answer is the third option 72=2^3*3^2
Use logarithmic differentiation to find the derivative of the function x^2+(y-cuberoot(x^2))^2=1
Answers
By applying logarithmic differentiation to the equation
\(x^2 + (y - ∛(x^2))^2 = 1\), we can find the derivative of y with respect to x. The derivative is given by \(dy/dx = -4x(y - ∛(x^2)) / (2x^2 + 3(y - ∛(x^2))^2)\).
To use logarithmic differentiation, we start by taking the natural logarithm of both sides of the equation: \(ln(x^2 + (y - ∛(x^2))^2) = ln(1).\) Applying the logarithmic property, we can rewrite the equation as
\(ln(x^2) + ln((y - ∛(x^2))^2) = 0.\)
Next, we differentiate both sides of the equation with respect to x. Using the chain rule and the fact that the derivative of ln(u) is du/u, we obtain:
\((2x/x^2) + (2(y - ∛(x^2))/ (y - ∛(x^2))) * (1/2(y - ∛(x^2))) * (d(y - ∛(x^2))/dx) = 0\).
Simplifying the equation, we have
\(2/x + (2(y - ∛(x^2))) / (2(y - ∛(x^2))) * (d(y - ∛(x^2))/dx) = 0\).
Canceling out common factors, we get:
\(2/x + d(y - ∛(x^2))/dx = 0\).
Rearranging the equation to solve for
\(d(y - ∛(x^2))/dx\), we have\(d(y - ∛(x^2))/dx = -2/x.\)
Finally, using the power rule for differentiation, we can express the derivative of y with respect to x as
\(dy/dx = -4x(y - ∛(x^2)) / (2x^2 + 3(y - ∛(x^2))^2).\)
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. 9. y= x
,y=0,x=4
Answers
The volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells is 486π cubic units.
To find the volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells, we can follow these steps:
First, let's sketch the region bounded by the curve y = x. This is a straight line passing through the origin with a slope of 1. It forms a right triangle in the first quadrant, with the x-axis and y-axis as its legs.
Next, we need to determine the limits of integration. Since we are rotating about the y-axis, the integration limits will correspond to the y-values of the region. In this case, the region is bounded by y = 0 (the x-axis) and y = x.
The height of each cylindrical shell will be the difference between the upper and lower curves. Therefore, the height of each shell is given by h = x.
The radius of each cylindrical shell is the distance from the y-axis to the x-value on the curve. Since we are rotating about the y-axis, the radius is given by r = y.
The differential volume element of each cylindrical shell is given by dV = 2πrh dy, where r is the radius and h is the height.
Now we can express the volume of the solid of revolution as the integral of the differential volume element over the range of y-values:
V = ∫[a, b] 2πrh dy
Here, [a, b] represents the range of y-values that define the region. In this case, a = 0 and b = 9 (as y = x, so the curve intersects y-axis at y = 9).
Substituting t
he values of r and h into the integral, we have:
V = ∫[0, 9] 2πy(y) dy
Simplifying, we get:
V = 2π ∫[0, 9] y^2 dy
Evaluating the integral, we have:
V = 2π [y^3/3] from 0 to 9
V = 2π [(9^3/3) - (0^3/3)]
V = 2π [(729/3) - 0]
V = 2π (243)
V = 486π
to learn more about integration.
https://brainly.com/question/31744185
#SPJ11
Solve each system by eliminati 1) 10x - 4y = 24 7x - 4y= 12
Answers
Answer:
Step-by-step explanation:
10x - 4y=24
7x -4y=12 multiply this equation by -1
-7x+4y=-12 we add it to the first and we get
3x=12
x=12/3=4
replace x with 3 in first equation
40-4y=24
40-24=4y
16=4y
y=4, x=4
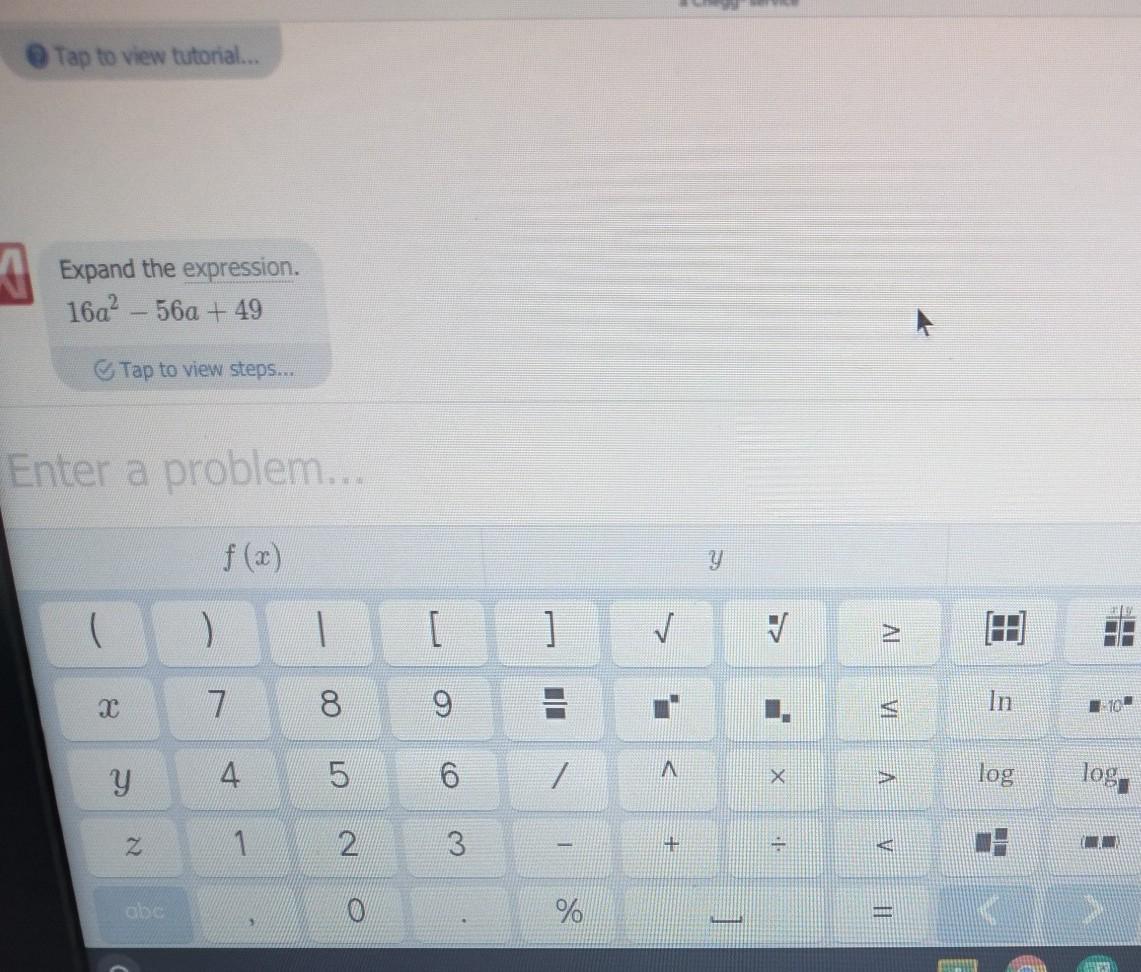
Answer please and thank you

Answers
Step-by-step explanation:
16a^2-56a+49
used the an app to find it