Problem 5. Apply the Rabin-Miller primality test to the following cases. In each case state if n probably prime or if it is composite. If possible also give factorization. (1) For n= 1729 using a = 671 (note that n-1 = 26 · 27). (2) For n= 104513 with a = 3 (you may use that n-1 = 26 · 1633)
Answers
To find a factorization of n, we can use the Pollard rho algorithm or another algorithm for factorization = 1.
The Rabin-Miller primality test is a probabilistic algorithm for determining whether a given number is prime or composite.
It is based on Fermat's Little Theorem and is widely used in cryptography.
To apply the Rabin-Miller primality test to a number n, we choose a random integer a between 1 and n-1, and then check whether a(n-1) ≡ 1 mod n and whether there exists a non-zero integer j such that a^(2^j * (n-1)) ≡ -1 mod n.
If either of these conditions is not satisfied, then n is composite. Otherwise, we repeat the test with a different random integer.
(1) For n = 1729 and a = 671:
First, we have n-1 = 26 * 27. We compute:
a(n-1) mod n = 671(26*27) mod 1729 = 1
Next, we look for a value of j such that a(2j * (n-1)) ≡ -1 mod n. We compute:
a(21 * (n-1)) mod n = 671(26*27/21) mod 1729 = 899
a(22 * (n-1)) mod n = 671(26*27/22) mod 1729 = 1
Since we found a value of j such that a(2j * (n-1)) ≡ -1 mod n, we conclude that n is probably prime.
(2) For n = 104513 and a = 3:
First, we have n-1 = 26 * 1633. We compute:
a(n-1) mod n = 3(26*1633) mod 104513 = 1
Next, we look for a value of j such that a(2j * (n-1)) ≡ -1 mod n. We compute:
a(20 * (n-1)) mod n = 3(26*1633/20) mod 104513 = 1
a(21 * (n-1)) mod n = 3(26*1633/21) mod 104513 = 11054
a(23 * (n-1)) mod n = 3(26*1633/23) mod 104513 = 1
For similar questions on factorization:
https://brainly.com/question/14067703
#SPJ11
Related Questions
3. Find the actual area of the hallway.
4. Find the actual area of the kitchen.

Answers
1/2 in x 5 in to get the area in inches
Multiply that by 6 to get the ft
(15 ft)
Kitchen:
3 in x 3 in
Multiple that by 6 to get the ft
(54 ft)
(REMEMBER: Final label is ft.)
Hallway = (1/2 in. (width) x (2 in. (length) + 3 in. (length)) x 6 ft. (actual size)
Hallway = (1/2 in. (width) x 5 in. (length)) x 6 ft. (actual size)
Hallway = 5/2 in. (area) x 6 ft. (actual size)
Hallway = 15 ft^2 (final answer)
Kitchen = (3 in. (width) x 3 in. (length)) x 6 ft. (actual size)
Kitchen = 9 in. (area) x 6 ft. (actual size)
Kitchen = 54 ft^2 (final answer)
help ????!!!! pls!!!

Answers
Answer:
You can use y − y1 = m(x − x1) and get 2-y= 1/6(9-3) so y = 1
Step-by-step explanation:
6sin^2 (x) + 6sin (x) + 1 = 0
solve and show steps for the graph ( i already have the graph )
Answers
To solve the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0, we can use algebraic methods and the unit circle to determine the values of x that satisfy the equation.
1. Start by rearranging the equation to a quadratic form: \(6sin^2(x)\) + 6sin(x) + 1 = 0.
2. Notice that the equation resembles a quadratic equation in terms of sin(x). Let's substitute sin(x) with a variable, such as u: \(6u^2\) + 6u + 1 = 0.
3. Solve this quadratic equation for u. You can use the quadratic formula or factorization methods to find the values of u. The solutions are u = (-3 ± √3) / 6.
4. Since sin(x) = u, substitute back the values of u into sin(x) to obtain the values for sin(x): sin(x) = (-3 ± √3) / 6.
5. To find the values of x, we can use the inverse sine function. Take the inverse sine of both sides: x = arcsin[(-3 ± √3) / 6].
6. The arcsin function has a range of [-π/2, π/2], so the values of x lie within that range. Use a calculator to find the approximate values of x based on the values obtained in step 5.
7. Plot the obtained x-values on the graph to show the solutions of the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0. The graph will illustrate the points where the curve intersects the x-axis.
For more such questions on algebraic, click on:
https://brainly.com/question/4344214
#SPJ8
On april 8th, a flower at blooming acres florist was 15. 0 centimeters tall. On april 16th, the flower was 17. 4 centimeters tall. If the flower grew at a constant rate, on what day was the flower 16. 5 centimeters tall?.
Answers
In linear equation , 13 April is day was the flower 16. 5 centimeters tall.
What are a definition and an example of a linear equation?
An equation with only one variable is referred to as a linear equation in one variable. It has the mathematical formula Ax + B = 0, where A and B can be any two real numbers, and x is an unknowable variable with just one possible value. A linear equation in one variable would be 9x + 78 = 18, for instance.Rate of change = 17.4 - 15/16 - 8
= 2.4/3
= 0.3 cm/day
Difference between 16.5 cm and 15 cm = 16.5 - 15 = 1.5 cm
Number of days required to grow from 15 cm to 16.5 cm = 1.5/0.3 = 5 days
Date on which the flower was 16.5 cm tall = 8th April + 5 = 13 April
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
If f(x)= 2x+1 &g(f(x))=4x^2+4x+3,find g(x) given that g(x) =ax^2+bx+c
Answers
The solution of the function g(x) is (-1/7)x² + (4/7)x + (6/7).
We know that g(f(x)) = 4x² + 4x + 3. This means that the input of g is actually the output of f.
To find g(x), we need to undo the composition of functions and get g(x) in terms of x. We can do this by working backwards. Let's start by finding f(g(x)):
f(g(x)) = 2g(x) + 1
Now, we know that g(f(x)) = 4x² + 4x + 3, which means that:
g(f(x)) = ag(x)² + bg(x) + c
Substituting f(x) = 2x + 1, we get:
g(2x + 1) = a(2g(x) + 1)² + b(2g(x) + 1) + c
Expanding the right-hand side, we get:
g(2x + 1) = 4ag(x)² + (4a + 2b)g(x) + (a + b + c)
We can now compare this equation with the one we got for g(f(x)):
g(f(x)) = ag(x)² + bg(x) + c
Comparing the coefficients of g(x) in both equations, we get:
4a + 2b = b => 4a = -b
Comparing the constant terms in both equations, we get:
a + b + c = 3
We now have two equations with three unknowns (a, b, and c). However, we can use the equation 4a = -b to eliminate one of the unknowns. Substituting -4a for b in the equation a + b + c = 3, we get:
a - 4a + c = 3 => -3a + c = 3 => c = 3 + 3a
We now have expressions for b and c in terms of a. Substituting these expressions into the equation 4a = -b, we get:
4a = -(-4a - 3a - 3) => 4a = 7a + 3 => a = -1/7
Substituting this value of a into our expressions for b and c, we get:
b = -4a = 4/7 c = 3 + 3a = 6/7
Therefore, g(x) = ax² + bx + c = (-1/7)x² + (4/7)x + (6/7).
To know more about expressions here
https://brainly.com/question/27850853
#SPJ4
The bar chart below shows the monthly energy bill for Wally's tackle shop.
Which of the listed months had bills between $40 and $50? Scroll down to
see all six answer options and check all that apply.
Energy bill (S)
70
60
50
40
30
20
10
January
February
March
April
Months
August
September
October
ՅզաaAON
December

Answers
Answer:
March, June, and November
Step-by-step explanation:
See attached image for the utility bills by month. Draw a line along the $40 and $50 lines on the y axis and select the months that fall within these two lines.

Abstractly Create two sets of data, each with five values, that
satisfy the following conditions.
The mean absolute deviation of Set A is less than the mean
absolute deviation of Set B.
The mean of Set A is greater than the mean of Set B.
Answers
The mean and MAD of the two sets are solved
Given data ,
Set A: {1,2,3,4,10}
Mean of Set A: (1 + 2 + 3 + 4 + 10) / 5 = 4
To find the mean absolute deviation (MAD), we first find the absolute difference of each value from the mean:
|1 - 4| = 3
|2 - 4| = 2
|3 - 4| = 1
|4 - 4| = 0
|10 - 4| = 6
Next, we find the average of these absolute differences:
MAD of Set A = (3 + 2 + 1 + 0 + 6) / 5 = 2.4
And ,
Set B: {1, 2, 3, 4, 5}
Mean of Set B: (1 + 2 + 3 + 4 + 5) / 5 = 3
To find the mean absolute deviation (MAD), we first find the absolute difference of each value from the mean:
|1 - 3| = 2
|2 - 3| = 1
|3 - 3| = 0
|4 - 3| = 1
|5 - 3| = 2
Next, we find the average of these absolute differences:
MAD of Set B = ( 2 + 1 + 0 + 1 + 2 ) / 5 = 1.2
Hence , mean absolute deviation of Set A is less than the mean absolute deviation of Set B and mean of Set A is greater than the mean of Set B
To learn more about mean click :
https://brainly.com/question/15526777
#SPJ1
I NEED HELPPP
PLS HELP

Answers
Answer:
85 m²
Step-by-step explanation:
*Multiply length times width (7m x 15m)
*Find the area of the missing space by multiplying the length times the width (4m x 5m)
*Subtract the missing space area from the first calculation
\( \large \bf \implies85 \: {m}^{2} \)
Step-by-step explanation:Area of Rectangle ABCF= Length × width
= (15 × 7) = 105 m²
Area of Rectangle DEGH= Length × width
= (5 × 4) = 20 m²
Area of the figure= Area of Rectangle ABCF - Area of Rectangle DEGH
= 105 m² - 20 m² = 85 m²

-2k-(-5)+1 combine like terms to create an equivalent expression
Answers
The resulting equivalent expression is -2k + 6
Equivalent expression.
Equivalent expression means an expressions that work the same even though they look different. If we said the two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value(s) for the variable(s).
Given,
Here we have the expression -2k - (-5) + 1
Now, we have to combine the like terms and then we have to solve it in order to find the equivalent expression.
First, we have to write the given expression,
=> -2k - (-5) + 1
Here we know that (-) x (-) = (+), therefore, the given expression is rewritten as follows:
=> -2k + 5 + 1
Here the only like term is the constant 5 and 1, so, we have to combine these constant, the we get the expression like the following;
=> -2k + (5 + 1)
No, we have to add the constant in order to get the equivalent expression,
=> - 2k + 6
Therefore, the equivalent expression i s -2k + 6.
To know more about Equivalent expression here.
https://brainly.com/question/28170201
#SPJ1
Question
Find the value of y
for the given value of x
.
y=1−2x;x=9
Answers
Answer:
y=-17
Step-by-step explanation:
1-2(9)=1-18=-17
Answer: y = -17
Step-by-step explanation:
Using PEMDAS, you need to do the multiplication first. 2 times x is 18, because the value of x is 9. You will then get 1 - 18. This is -17, so y = -17. I hope that this helped! :)
i rented a gym for $150.00 for 30 students. another time i rented the gym for $270.00 for 70 students. charge for 50 students
Answers
Answer:
y = 3x + 60
Step-by-step explanation:
The figure shows a rhombus ABCD. The diagonal DB is produced to E such that BC = BE and CDE = 46°.
Find
(I) BAD
(ii) BCE

Answers
Answer:
(i) 88°
(ii) 23°
Step-by-step explanation:
See the picture below.
The numbers added in red are the angle measures. The numbers added in black are the order in which each angle measure was written.
ABCD is a rhombus, so all sides are congruent.
Triangle BCD is isosceles with sides DC and BC congruent, so <DBC is congruent to <BDC. From the sum of the measures of the angles of a triangle, we get m<DCB. Opposite angles of a rhombus are congruent, so m<A = m<DCB. From the sum of the measures of the angles of a triangle and from isosceles triangle ADB we get m<ADB and m<ABD. From m<DBC and supplementary angles, we get m<CBE. From isosceles triangle BCE, we get m<BCE.

Round 609635.782852 to the nearest thousand.
Answers
Answer:
610000
Step-by-step explanation:
Srry i misread that i thought it said round to the nearest thousandth f
After rounding the number to the nearest thousand we get 609635.783
Here,
The given number to round nearest thousand is 609635.782852
What is rounding off of a number?
Rounding off means a number is made simpler by keeping its value intact but closer to the next number.
Now,
In rounding off a number nearest thousand we can write a number up to 3 decimal places
So after rounding 609635.782852 to the nearest thousands we get,
609635.783
Learn more about the Rounding off of a number visit:
https://brainly.in/question/5838592
#SPJ2
Tyrone is having an 80-foot tree removed from his front yard. One of the tree surgeons ties a rope to the top of the tree and stands 60 feet from the base of the tree while his partner saws through the tree. The rope will help them control the direction in which the tree falls. In the diagram below, side X represents the length of rope needed
Answers
Answer:
..........
Step-by-step explanation:
Answer:
jj
Step-by-step explanation:
he 134 sixth grade students sit together in the auditorium. Each row has 12 seats. How many rows do the sixth graders need
Answers
Answer:
Approximately 11.1666666667 rows
Step-by-step explanation:
134/12= 11.1666666667
Answer:
12 rows
Step-by-step explanation:
(134 students) / (12 students/row) = 11 2/12 rows
The 6th-graders will need 12 rows of seats. The last row will not be filled.
write and expression for the perimeter of the polygon. simplify the expression. (marking brainiest)

Answers
Step-by-step explanation:
Expression = x + 2x + 7 + 3x + 1
Simplication
x + 2x + 7 + 3x + 1
6x + 8
Suppose K⊆Rn is compact, f:K→R is continuous, and ϵ>0. Show that there is a number A>0 such that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
Answers
By using the concept of compact set, it can be proved that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
What is compact set?
A set K is said to be compact if every open cover of K has a finite subcover.
Let K⊆Rn is compact f:K→R is continuous, and ϵ>0
Let there exist \(x_n, y_n\) ∈ K such that |f(\(x_n\))−f(\(y_n\))| > n∥\(x_n\)−\(y_n\)∥+ϵ,
Since K is compact there is a subsequence \(x_{nk}\) and \(y_{nk}\) of \(x_n, y_n\) respectively such that \(x_{nk}\) converges to x and \(y_{nk}\) converges to y.
So, |f(\(x_{nk}\))−f(\(y_{nk}\))| > \(n_k\)∥\(x_{nk}\)−\(y_{nk}\)∥+ϵ,
Since f is continuous,
We can write
|f(x)−f(y)| > \(n_k\)∥x - y∥+ϵ,
This is true for infinite many \(n_k\)
So ||x - y|| = 0
|f(x) - f(y)| > ϵ, a contradiction since f is continuous
So, there is a number A>0 such that
|f(x)−f(y)|≤A∥x−y∥+ϵ,∀x,y∈K.
To learn more about compact set, refer to the link-
https://brainly.com/question/17175854
#SPJ4
Find (g • f) (3)
f(x) = |x+2|
g(x) = -x^2
a. -25
b. 1
c. 4
d. -15
Answers
Step-by-step explanation:
Given
f(x) = |x + 2|
g(x) = - (x)²
Now
(g•f) (3) = g ( 3 + 2 )
= g(5)
= - (5)²
= -25
Hope it will help :)
3. A company is designing a juice box. The box is in the shape of a
rectangular prism. The base of the box is 6 inches by 2 inches and
the box is 4 inches high tice fills 90% of the box volume find the
volume of juice in the box
Answers
Answer:
48in^2 or just 48 dont forget to include the inches and squared
Step-by-step explanation:
is this correct or it needs any fixing

Answers
Let the random variable h represent the height of a woman in the population. P(h<60) represents the probability of randomly selecting a woman with height less than 60 inches. Based on the information given, the probability can be found using either the discrete model or the normal model. 1. Give an example of a probability h that can be found using the discrete model but not the normal model
Answers
The probability of h that can be found using the discrete model but not the normal model is 0.03.
A discrete probability distribution or DPD (also known as a discrete probability model) records all possible values of a discrete random variable and gives their probabilities.
The normal probability model involves when the distribution of the continuous outcome conforms reasonably well to a normal or Gaussian distribution, which resembles a bell-shaped curve.
H represents the height of women
Determine P ( H < 60 ) using either a discrete or normal model
using discrete model
P ( H < 60 ) = ∑ relative frequencies of the women with height < 60 inches
P ( H < 60 ) = 0.01 + 0.02 = 0.03
To know more about Gaussian distribution, here
https://brainly.com/question/29734279
#SPJ4
You want to estimate the average GMAT score for all students who took the Logitano GMAT Preparation course during the past 2 years. You select a random sample of 100 such students from a comprehensive list of all students who took the course over the last two years and find that the average GMAT score for the sample was 1040. Suppose now you build a 95% confidence interval estimate of the average score for the population of Logitano students represented here and the interval turns out to be 1040 ± 10 points. How would you interpret your result?
We can be 95% confident that the interval 1030 to 1050 contains the average score for the entire population of Logitano students.
The score for 95% of all Logitano students will be between 1030 and 1050.
There is a 5% chance that not all Logitano students scored between 1030 and 1050.
We can be 95% confident that all of Logitano students scored between 1030 and 1050.
Ninety-five percent of the scores for all Logitano students will be between 1030 and 1050.
Answers
The correct interpretation is: We can be 95% confident that the interval 1030 to 1050 contains the average score for the entire population of Logitano students.
The statement is referring to a confidence interval estimate for the average score of the entire population of Logitano students who took the GMAT Preparation course during the past two years. The interval 1030 to 1050 is constructed based on a sample of students and provides a plausible range for the true population average.
The interpretation "We can be 95% confident that the interval 1030 to 1050 contains the average score for the entire population of Logitano students" means that if we were to repeat the process of taking samples and constructing confidence intervals multiple times, about 95% of those intervals would contain the true average score of all Logitano students who took the course.
In other words, the statement implies that we have a high level of confidence that the true population average score falls within the interval 1030 to 1050. This level of confidence is derived from the statistical methods used to estimate the population parameter (average score) based on the sample data. The 95% confidence level indicates that there is a 95% probability that the true population average lies within the stated interval.
It's important to note that this interpretation is based on the assumptions and conditions of the statistical analysis performed, such as the random sampling of students, the validity of the estimation method, and the assumption of normality in the population distribution.
Learn more about population from
https://brainly.com/question/25896797
#SPJ11
Find the slope and Y interact from the following graph of liner liner equation

Answers
Answer:
A
Step-by-step explanation:
slope is rise over run 4/1 so the slope is 4 and intercept is 3.
You are solving a measurement problem where the numbers 4.5160 x 10−3, 2.09 x 107, and 5.8 x 103 are multiplied. how many significant digits should the product have? 2 1 5 3
Answers
The number of significant digits the product should have = 2
The given numbers are:
\(4.5160 \times 10^{-3}\\ 2.09 \times 10^7\\ 5.8 \times 10^3\)
We first multiply them.
\(4.5160 \times 10^{-3}\times 2.09 \times 10^7\times 5.8 \times 10^3 = 54.743\times10^7\)
In measurement problems, we usually write it as \(5.474\times10^7\)
Significant digits are the numbers which decide the precision and accuracy in measurement problems.
The fewest number of significant digits in each factor of multiplication is considered as the significant digits of the product.
So number of significant digits in \(4.5160\times10^{-3}\) = 5
Number significant digits in \(2.09\times10^7\) = 3
Number of significant digits in \(5.8\times10^3\) = 2
So the product should be rounded into 2 significant digits.
So the product, \(5.474\times10^7\)= \(5.5\times10^7\) with 2 significant figures.
Learn more about significant digits at https://brainly.com/question/24491627
#SPJ4
find the slope of (0,-1) (-1,-4)
Answers
The slope of the line that passes through point (0,-1) and (-1,-4) is 3.
What is the slope of the line that passes through the given points?Slope is simply expressed as change in y over the change in x.
Slope m = ( y₂ - y₁ )/( x₂ - x₁ )
Given the data in the question;
Point 1( 0,-1 )
x₁ = 0y₁ = -1Point 2( -1,-4 )
x₂ = -1y₂ = -4To determine the slope of the line, plug the coordinates into the slope formula above.
Slope m = ( y₂ - y₁ )/( x₂ - x₁ )
Slope m = ( -4 - (-1) )/( -1 - 0 )
Slope m = ( -4 + 1 )/( -1 )
Slope m = ( -3 )/( -1 )
Slope m = 3
Therefore, the slope of the line is 3.
Learn more about slope formula here: brainly.com/question/24578307
#SPJ1
LONG DIVISiON 1\8 pls ASAP
Answers
Answer:
8
Step-by-step explanation:
The instantaneous rate of change of the value of a certain investment (P) is proportional to its value. That is to say dP/dt=rP. If r = 2 and P(0)=1500 P(t) =
Answers
The value of investment P at any time t is given by the function P(t) = 1500e^(2t). This equation shows that the value of investment P grows exponentially with time, with a rate of growth proportional to its instantaneous value.
The given differential equation, dP/dt=rP, implies that the instantaneous rate of change of the value of investment P is proportional to its value at any given time. Here, r is the proportionality constant, which is equal to 2. If P(0) = 1500, it means that the initial value of investment P was 1500 units.
To find the value of P at any time t, we need to solve the differential equation. Integrating both sides, we get:
ln(P) = rt + C
where C is the constant of integration. To determine the value of C, we can use the initial condition P(0) = 1500. Substituting t = 0 and P = 1500 in the above equation, we get:
ln(1500) = r(0) + C
C = ln(1500)
Thus, the equation for the value of investment P at any time t is given by:
ln(P) = 2t + ln(1500)
P(t) = e^(2t+ln(1500))
Simplifying the above equation, we get:
P(t) = 1500e^(2t)
Therefore, the value of investment P at any time t is given by the function P(t) = 1500e^(2t). This equation shows that the value of investment P grows exponentially with time, with a rate of growth proportional to its instantaneous value.
To know more about instantaneous rate visit :
https://brainly.com/question/30782681
#SPJ11
Kirito's Clothing Store buys coats for $80 and sells them for $140.
What is the percent markup on the price of the coats?
Answers
Answer:
75%
Step-by-step explanation:
80 x 0.75 = 60
80 + 60 = 140
can someone please help me im strugging bad
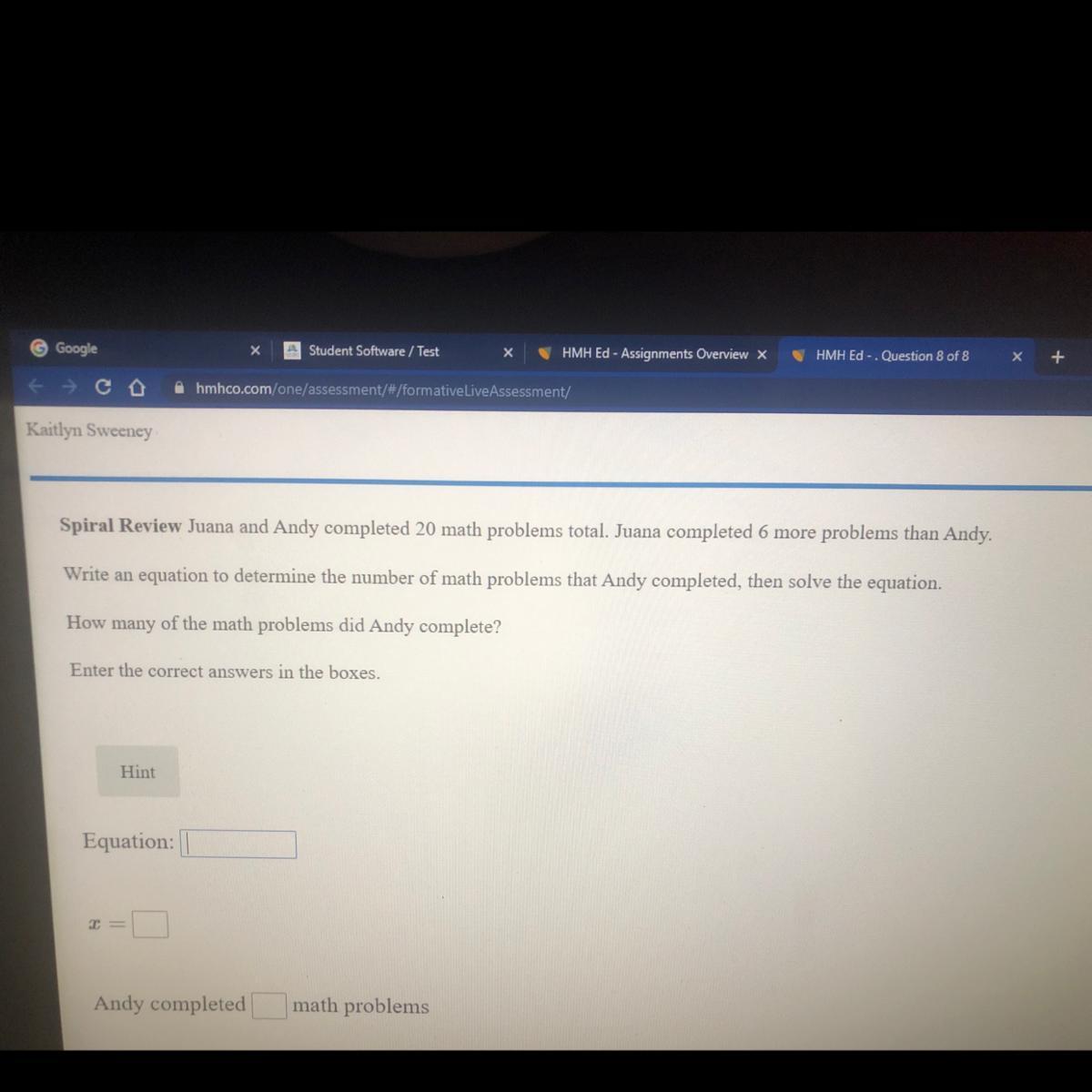
Answers
Answer:
120
Step-by-step explanation:
Answer:
x+6y=20
x=8, y=2
Andy did 8 problems
Step-by-step explanation:
Can anyone help me ASAP!

Answers
Answer:
It should be 16
Answer:
18.78
Step-by-step explanation:
\(a^{2} + b^{2} = c^{2} \\8^{2} + 17^2 = c^2\\64 + 289 = 353\\\sqrt{353} = 18.78\)