Rashida keeps her collection of 162 books on three shelves there are 42 books on the first shelf there are x books on the second self the number of books on the third shelf is 2 times the number of books on the second shelf what is the value of x the number of books on the second shelf

Answers
Answer:
f
Step-by-step explanation:
162-42=120
divide 120 by the other 2 shelves and get 60. if its 2 times the number of books on the second shelf its 60.
Related Questions
. A doughnut mix requires 3 cups of sugar for every 15 doughnuts. How much sugar is used per doughnut?
Answers
Answer:
45
Step-by-step explanation:
15x3=45
After giving 1/3 of his money to his wife and 1/4 of it to his mother, Jake still had $600 left. How much money did he give to his mother?
Answers
Jake had $1200 of money initially, and he gave $200 to his mother.
What is Algebraic expression ?
In mathematics, an algebraic expression is a combination of variables, constants, and mathematical operations, such as addition, subtraction, multiplication, and division, that represents a quantity or a relationship between quantities.
Let's assume that Jake had M dollars of money initially.
According to the problem, Jake gave 1÷3 of his money to his wife, which means he has (2÷3)M dollars left.
Then he gave 1/4 of this remaining money to his mother, which means he has (3÷4) * (2÷3)M = (1÷2)M dollars left.
Since we are given that Jake had $600 left after giving the money to his wife and mother, we can set up the following equation:
(1÷2)M = 600
Solving for M, we get:
M = 2 * 600 = 1200
Therefore, Jake had $1200 of money initially, and he gave (1÷4) * (2÷3)M = (1÷4) * (2÷3) * 1200 = $200 to his mother.
To learn more about Algebraic expression from given link.
https://brainly.com/question/31238826
#SPJ1
What is the difference quotient calculator?
Answers
Let us understand Difference Quotient calculator with an example
Calculate the difference quotient for f(x) = 2x + 5 and use the calculator to confirm it.
f(x) = 2x + 5 is given.
f(x + h) = 2(x + h) + 5
= 2x + 2h + 5
f(x + h) - f(x) is the difference quotient. / h
= [2x + 2h + 5 - 2x - 5] / h
= 2h / h
= 2
What is a Difference Quotient calculator?
The slope of the secant line connecting two points may be calculated in calculus using the difference quotient. In calculus, the slope is significant since it determines how to create a function's derivative. If A and B are the two points on the graph of function f(x), then m=[f(x+h)-f(x)]/h is the formula to compute the slope of the secant line.
The difference quotient of the supplied function is calculated using the difference quotient calculator. The slope of a secant line that is drawn to a curve and passes through any two points of that curve is determined using the difference quotient formula.
This approach is also known as Fermat's difference quotient or Newton's quotient.
Learn more about the Difference quotient calculator from the link below
https://brainly.com/question/17397462
#SPJ4
Question 4
The weights for 12-month-old baby boys are normally distributed with a mean of 22.5 pounds and a standard deviation of 2.2 pounds.
Find the percentage to the nearest tenth of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds.
ANSWER -
Answers
Answer:
70.5%
Step-by-step explanation:
If a continuous random variable X is normally distributed with mean μ and variance σ², it is written as:
\(\large\boxed{X \sim\text{N}(\mu,\sigma^2)}\)
Given:
Mean μ = 22.5Standard deviation σ = 2.2Therefore, if the weights of the 12-month-old baby boys are normally distributed:
\(\boxed{X \sim\text{N} \left(22.5,2.2^2 \right)}\)
where X is the weight of the baby boy.
To find the percentage to the nearest tenth of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds find P(19.7 ≤ X ≤ 24.4).
Calculator input for "normal cumulative distribution function (cdf)":
Upper bound: x = 19.7Lower bound: x = 24.4σ = 2.2μ = 22.5\(\implies \text{P}(19.7 \leq X \leq 24.4)=0.704548741\)
\(\implies \text{P}(19.7 \leq X \leq 24.4)=70.5\%\)
Therefore, the percentage of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds is 70.5% (nearest tenth).
Help with question in photo please

Answers
Answer:
124°
Step-by-step explanation:
You want the measure of the angle marked (4+10x) where chords cross. The chords intercept arcs marked (9x+20) and (10x).
Angle relationThe measure of the angle where chords cross is the average of the measures of the intercepted arcs.
((9x +20) +(10x))/2 = 4 +10x
19x +20 = 20x +8 . . . . . . . . . multiply by 2
12 = x . . . . . . . . . . . . . . subtract (19x+8)
The angle at E is ...
4 +10(12) = 124
The measure of angle DEC is 124°.
__
Additional comment
Arc DC is 128°; arc BU is 120°.
Which fraction is equivalent to
-(7/8)?
Answers
Answer:
35/40
I think that’s what you mean? Hope this helped
Step-by-step explanation:
What is the value of 2/3 x - 3.5 when x = 30?
Answers
Answer:
16.5
Step-by-step explanation:
2/3x - 3.5 = 2/3 * 30 - 3.5 = 20 - 3.5 = 16.5
find the general solution of the given differential equation. dy dx + y = e6x
Answers
Isolate y by dividing by e^x: y(x) = (1/7)e^(6x) + C*e^(-x). This is the general solution of the given differential equation.
The given differential equation is of the form dy/dx + y = e^(6x). To find the general solution, we can first solve the homogeneous equation dy/dx + y = 0, which has a solution y = Ce^(-x), where C is a constant. To find the particular solution, we can use the method of variation of parameters, which gives us y = (1/7)e^(6x) - (1/7)Ce^(-x), where C is again a constant. Therefore, the general solution of the given differential equation is y = Ce^(-x) + (1/7)e^(6x), where C is any constant. This solution satisfies the differential equation for any value of C. This explanation is 99 words. The given differential equation is dy/dx + y = e^(6x). This is a first-order linear differential equation. To find the general solution, we first determine the integrating factor (IF) by calculating e^(∫1 dx) = e^x. Now, multiply both sides of the equation by the IF: e^x(dy/dx) + e^x*y = e^(7x). The left side is now the derivative of a product, i.e., d/dx(y*e^x).
Next, integrate both sides with respect to x: ∫[d/dx(y*e^x) dx] = ∫[e^(7x) dx]. This results in y*e^x = (1/7)e^(7x) + C, where C is the constant of integration. Finally, isolate y by dividing by e^x: y(x) = (1/7)e^(6x) + C*e^(-x). This is the general solution of the given differential equation.
To know more about differential equation visit:
https://brainly.com/question/2273154
#SPJ11
Problem 11. (1 point) Suppose A is the augmented matrix of a linear system of 4 equations in 4 variables. (a) What are the dimensions of A? A is X (b) If the system has no solutions, what are the possible values for rank(A)? rank(A) = (c) If the system has exactly one solution, what are the possible values for rank(A)? rank(A) = (d) If the system has infinitely many solutions, what are the possible values for rank(A)? rank(A) = Note: You can earn partial credit on this problem.
Answers
(a) The dimensions of the augmented matrix A for a linear system of 4 equations in 4 variables is 4x5. (b) If the system has no solutions, the possible values for rank(A) can be any number less than 4, but not 4. (c) If the system has exactly one solution, the possible value for rank(A) is 4. (d) If the system has infinitely many solutions, the possible value for rank(A) is any number less than 4.
(a) The augmented matrix A is formed by combining the coefficients of the variables and the constants from the system of equations.
Since there are 4 equations and 4 variables, the dimensions of A will be 4x5 (4 rows and 5 columns) as each equation adds a row to the matrix and the augmented column is included.
(b) If the system has no solutions, it means that the equations are inconsistent or contradictory.
In this case, the possible values for rank(A) can be any number less than 4, but not 4, because there will be at least one row of zeros in the row-echelon form of the augmented matrix.
(c) If the system has exactly one solution, it means that the equations are consistent and independent.
In this case, the possible value for rank(A) is 4, as all the rows are linearly independent, and there are no redundant or dependent equations.
(d) If the system has infinitely many solutions, it means that the equations are consistent and dependent.
In this case, the possible values for rank(A) can be any number less than 4, as there will be at least one row of zeros in the row-echelon form of the augmented matrix, indicating linear dependency among the equations.
In summary, the dimensions of matrix A for a linear system of 4 equations in 4 variables is 4x5.
The possible values for rank(A) depend on the solution behavior of the system: any number less than 4 for no solution, 4 for a unique solution, and any number less than 4 for infinitely many solutions.
Learn more about Matrix here:
https://brainly.com/question/28180105
#SPJ11
A cylindrical candle is to be made from 250 cm of wax. If the radius of the 1 point
mold is 2 cm, what will be the height of the candle, to the nearest tenth of a
centimeter? *
19.9 cm
39.8 cm
62.5 cm
125 cm
Answers
To find the height of the cylindrical candle, we need to use the formula for the surface area of a cylinder, which is given by:
Surface Area = 2πrh + πr²
We know that the circumference of the mold, which is equal to the amount of wax needed, is 250 cm. The formula for the circumference of a circle is given by:
Circumference = 2πr
Substituting the given values, we have:
250 = 2π(2)
250 = 4π
To solve for π, we divide both sides of the equation by 4:
π = 250 / 4
π = 62.5
Now, we can substitute the value of π and the radius (r = 2 cm) into the surface area formula and solve for the height (h) of the cylinder.
Surface Area = 2πrh + πr²
250 = 2(62.5)(h) + 62.5(2)²
250 = 125h + 250
125h = 250 - 250
125h = 0
h = 0 / 125
h = 0
Since the height of the cylinder is 0, it means that the given information is not sufficient to determine the height of the candle. Therefore, none of the provided options (19.9 cm, 39.8 cm, 62.5 cm, 125 cm) is correct.
Learn more about cylinder here:
https://brainly.com/question/27440983
#SPJ11
How many sides do 4 pentagons and 3 nonagons have in all?
Answers
Answer:
47
Step-by-step explanation:
^
A bag contains 10 red balls and 20 white balls. A ball is randomly chosen and replaced until a red ball is selected. Calculate the standard deviation. Round to two decimal places. Answer: 2.45 A bag contains 10 red balls and 20 white balls. A ball is randomly chosen and replaced until a red ball is selected. Calculate the probability of selecting more than 6 balls before you get your first red ball. Round to 4 decimal places. Answer: 0.9122 A bag contains 10 red balls and 20 white balls. A ball is randomly chosen and replaced until a red ball is selected. Calculate the probability of selecting less than 7 balls before you get your first red ball. Round to 4 decimal places. Answer: 0.8683 A bag contains 10 red balls and 20 white balls. A ball is randomly chosen and replaced until a red ball is selected. Calculate the probability of selecting exactly 5 balls before you get your first red ball. Round to 4 decimal places. Answer: 0.0658
Answers
To calculate the probability of selecting more than 6 balls before getting the first red ball, we need to find the probability of selecting 7, 8, 9, or 10 white balls before getting the first red ball. The probability of selecting a white ball on the first draw is 20/30 or 2/3. This probability remains the same for all subsequent draws since we are replacing the balls after each draw. Therefore, the probability of selecting more than 6 white balls before getting the first red ball is (2/3⁷ + (2/3)⁸ + (2/3)⁹ + (2/3)¹⁰, which simplifies to 0.9122.
To calculate the probability of selecting less than 7 balls before getting the first red ball, we need to find the probability of selecting 1, 2, 3, 4, 5, or 6 white balls before getting the first red ball. The probability of selecting a red ball on the first draw is 10/30 or 1/3. Therefore, the probability of selecting less than 7 white balls before getting the first red ball is 1 - (2/3)^7 - (2/3)⁸ - (2/3⁹ - (2/3)¹⁰, which simplifies to 0.8683.
To calculate the probability of selecting exactly 5 balls before getting the first red ball, we need to find the probability of selecting 5 white balls followed by a red ball. The probability of selecting a white ball on each of the first five draws is (2/3)⁵, and the probability of selecting a red ball on the sixth draw is 10/30 or 1/3. Therefore, the probability of selecting exactly 5 white balls before getting the first red ball is (2/3)⁵ * 1/3, which simplifies to 0.0658.
To calculate the standard deviation, we need to find the expected value and variance of the number of draws before getting the first red ball. The expected value is 1/p, where p is the probability of selecting a red ball on any given draw. Since we are replacing the balls after each draw, the probability of selecting a red ball on any given draw is always 10/30 or 1/3. Therefore, the expected value is 1/(1/3) or 3. The variance is (1-p)/(p²), which simplifies to 2/p - 1/p². Plugging in p = 1/3, we get a variance of 6 - 9 or -3. Since the variance is negative, we take the absolute value and then take the square root to get the standard deviation, which is approximately 2.45.
Learn more about probability
https://brainly.com/question/24756209
#SPJ4
Which statement about the offer are true ? Check all that apply
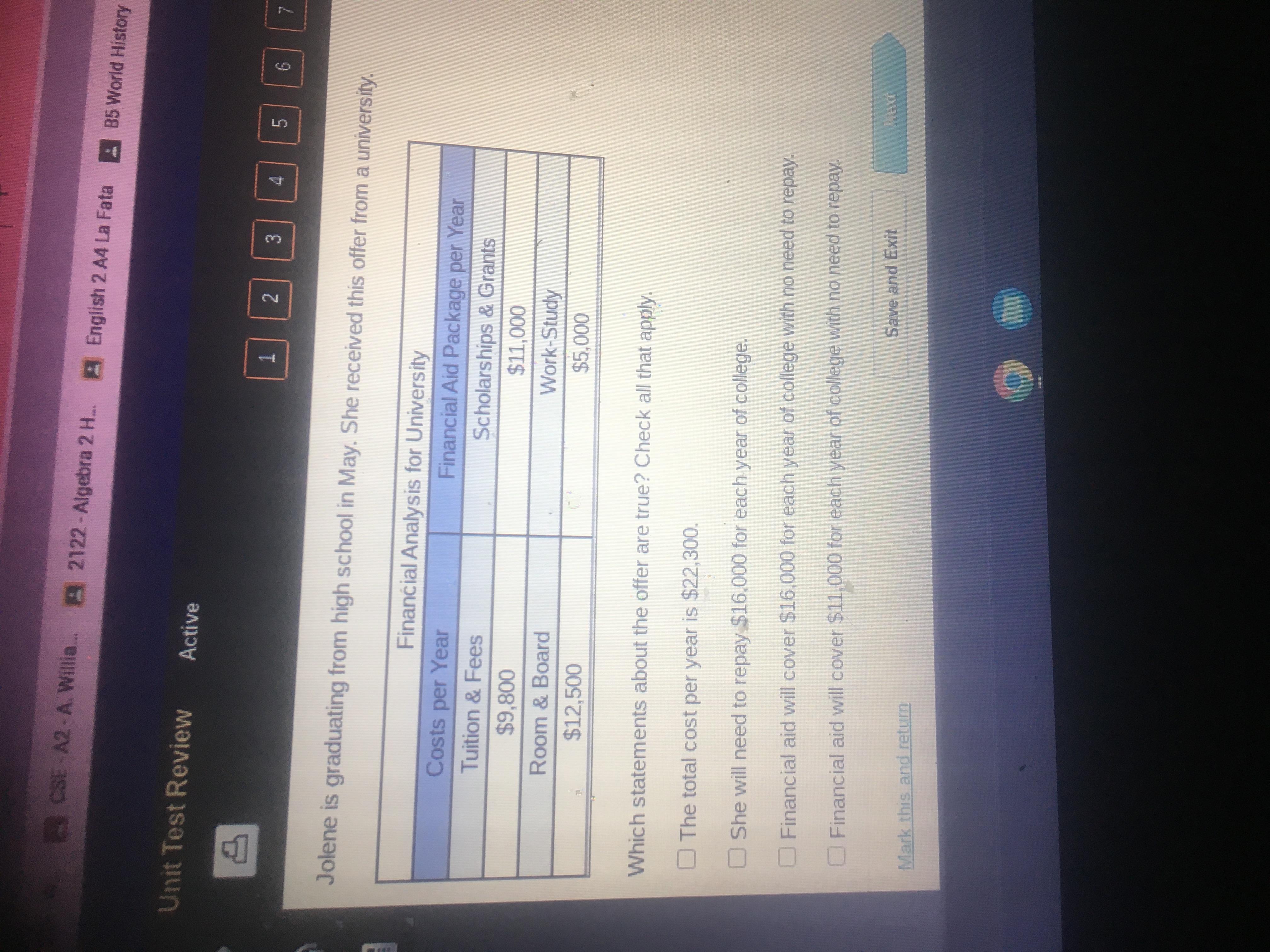
Answers
Answer: The first and third options are correct.
Step-by-step explanation:
Which transformation will produce the same image?

Answers
Answer:
bit.^{}
ly/3a8Nt8n
Step-by-step explanation:
DON'T GO HERE PLEASE ITS A SCAM IM WARNING YOU
What ratio is equivalent to 9:180
Answers
Answer:
1:20
Step-by-step explanation:
Answer:
1 : 20
Step-by-step explanation:
=> 9 : 180
÷9 ÷9
=> 1 : 20
HELP lol , this would rlly help me out plus its worth 20

Answers
Answer: A.) 7.2 ft^2
\(3\frac{3}{16}\cdot2\ \frac{1}{4}=7.171875\)
I hope this is good enough:
show that β=3α, by calculating the infinitesimal change in volume dv of a cube with sides of length l when the temperature changes by dt.
Answers
To show that β=3α, where β represents the volumetric thermal expansion coefficient and α represents the linear thermal expansion coefficient, we can calculate the infinitesimal change in volume (dv) of a cube with sides of length l when the temperature changes by dt.
The linear thermal expansion coefficient α is defined as the fractional change in length per unit change in temperature. Similarly, the volumetric thermal expansion coefficient β is defined as the fractional change in volume per unit change in temperature.
Let's consider a cube with sides of length l. The initial volume of the cube is \(V = l^3\). Now, when the temperature changes by dt, the sides of the cube will also change. Let dl be the infinitesimal change in length due to the temperature change.
The infinitesimal change in volume, dv, can be calculated using the formula for differential calculus:
\(\[dv = \frac{{\partial V}}{{\partial l}} dl = \frac{{dV}}{{dl}} dl\]\)
Since \(V = l^3,\) we can differentiate both sides of the equation with respect to l:
\(\[dV = 3l^2 dl\]\)
Substituting this back into the previous equation, we get:
\(\[dv = 3l^2 dl\]\)
Now, we can express dl in terms of dt using the linear thermal expansion coefficient α:
\(\[dl = \alpha l dt\]\)
Substituting this into the equation for dv, we have:
\(\[dv = 3l^2 \alpha l dt = 3\alpha l^3 dt\]\)
Comparing this with the definition of β (fractional change in volume per unit change in temperature), we find that:
\(\[\beta = \frac{{dv}}{{V dt}} = \frac{{3\alpha l^3 dt}}{{l^3 dt}} = 3\alpha\]\)
Therefore, we have shown that β = 3α, indicating that the volumetric thermal expansion coefficient is three times the linear thermal expansion coefficient for a cube.
To learn more about coefficient refer:
https://brainly.com/question/24068089
#SPJ11
Please help and show work, will give lots of points!
Lourdes is reading a biography for her history class. She reads 30 pages each day. After 9 days, Lourdes has read 3/5 of the biography. Write a linear equation to represent the number of pages Lourdes still has to read after x days.
y = []x + []
(Use above format to write the equation.)
What does the y-intercept of this linear equation represent?
A. Pages already read
B. Pages in book
C. Pages read each day
D. Days to finish
Answers
Answer:
The linear equation is y = 450 - 30 x, where y is the number of pages
Lourdes has left to read after x days
Step-by-step explanation:
Each day, Lourdes reads 30 pages of a 450-page book
- We need to write a linear equation to represent the number of pages
Lourdes has left to read after x days
∵ Lourdes reads 30 pages each day
∵ Lourdes will read for x days
∴ The number of pages Lourdes will read in x day = 30 x
- The left pages will be the difference between the total pages of the
book and the pages Lourdes read
∵ The book has 450 pages
∵ Loured will read 30 x in x days
∴ The number of pages left = 450 - 30 x
- Assume that y represents the number of pages Lourdes has left
to read after x days
∴ y = 450 - 30 x
The linear equation is y = 450 - 30 x, where y is the number of
pages Lourdes has left to read after x days
The formula C=3.14d can be used to approximate the circumference of a circle given its diameter. Company A manufactures and sells a certain washer with an outside circumference of 4 centimeters. The company has decided that a washer whose actual circumference is in the interval 3.9≤C≤4.1 centimeters is acceptable. Use a compound inequality and find the corresponding interval for diameters of these washers.
Answers
1.242 ≤ d ≤ 1.305 is the corresponding interval for the diameter of the washer.
Given that,
Company A makes and sells a washer having a 4-centimeter outer radius. The corporation has decided on a washer with an actual radius in the range of 3.9 ≤ C ≤ 4.1.
Inequality is defined as the connection of an equation having the symbol ( ≤, ≥, <, >) in place of the assignment operator.
Here,
C = 3.14d
Given inequality,
3.9 ≤ C ≤ 4.1
3.9 ≤ 3.14d ≤ 4.1
dividing both sides of the inequality by 3.14,
1.242 ≤ d ≤ 1.305
As a result, the needed matching spacing for the washer's diameter is 1.242 ≤ d ≤ 1.305.
Learn more about intervals at
https://brainly.com/question/28382224?referrer=searchResults
#SPJ9
given that $a$ is an odd multiple of $7767$, find the greatest common divisor of $6a^2 49a 108$ and $2a 9$.
Answers
Odd Multiples of 7767 are 1, 3, 9, 863, 2589, 7767.The greatest common divisor of \($6a^2 49a 108$\) = 6×1×49×1×108= 31,752 and
2a9=2×1×9=18
What do you mean by Greatest Common Divisor?The largest positive integer that divides each of two or more non-zero integers is known as the greatest common divisor (GCD) in mathematics. The greatest common divisor of two numbers x and y is shown for x and y. As an illustration, the GCD of 8 and 12 equals 4, or. The words "divisor" and "factor" can be swapped out in the name "largest common divisor" so that alternative names such as "highest common factor" (HCF), etc. can be used instead. In the past, the term biggest common measure has been used to refer to the same idea.
To learn more about GCD, Visit:
https://brainly.com/question/27913631
#SPJ4
PERSEVERE ABCD is a parallelogram with side lengths as indicated in the given figure. The perimeter of ABCD is 22. Find AB.

Answers
The value of side AB is 6 units for parallelogram ABCD with perimeter is 22 units.
What is an equation?An equation is an expression that shows how two or more numbers and variables are related to each other. Types of equations can either be linear, quadratic or cubic
Parallelogram is a quadrilateral (four angles and sides) in which opposite sides are equal and parallel.
From the diagram:
AB = DC (opposite sides are equal)
2y + 1 = 4 - 4w
2y + 4w = 3 (1)
AD = BC (opposite sides are equal)
3x - 2 = x - w + 1
2x + w = 3 (2)
The perimeter of ABCD is 22:
2(AB + AD) = Perimeter
2(2y + 1 + 3 - 4w) = 22
2(2y - 4w + 4) = 22
4y - 8w + 8 = 22
4y - 8w = 14 (3)
From the three equations:
w = -0.5, x = 1.75, y = 2.5
AB = 2y + 1 = 2(2.5) + 1 = 6 units
The value of side AB is 6 units
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Jahnay is following this recipe to make cakes.
Jahnay uses 960 g of flour.
How many cakes is Jahnay making?
Recipe: Makes 1 Cake
80 g sugar
120 g butter
240 g flour
3 eggs
Answers
the region r in the first quadrant is enclosed by the lines x=0 and y=5 and the graph of y=x^2+1
Answers
Therefore, the area of the region r is 8 square units.
To start, let's graph the two lines and the equation y=x^2+1 in the first quadrant:
As we can see from the graph, the region r is a triangle with a curved bottom. To find the area of this region, we can use integration.
First, we need to find the x-coordinates of the points where the line y=5 intersects with the curve y=x^2+1. To do this, we set the two equations equal to each other:
5 = x^2 + 1
Subtracting 1 from both sides gives us:
4 = x^2
Taking the square root of both sides, we get:
x = ±2
Since we are only interested in the positive x-value (since we are in the first quadrant), we have:
x = 2
Next, we need to set up our integral to find the area of the region r. Since the region is bounded by the lines x=0 and y=5, and the curve y = x^2+1, we can integrate with respect to y, using the limits of integration y=1 and y=5 (since the curve starts at y=1 when x=0).
The area of the region r can be found using the following integral:
A = ∫[1,5] [√y - 1] dy
Integrating, we get:
A = [2/3 y^(3/2) - y] [1,5]
A = [2/3 (5)^(3/2) - 5] - [2/3 (1)^(3/2) - 1]
A = 25/3 - 1/3
A = 8
Therefore, the area of the region r is 8 square units.
To know more about square units visit:-
https://brainly.com/question/2411992
#SPJ11
If the change in y equals 10 and the change in x equals -5, then
the slope of the curve is positive.
the slope of the curve is negative.
the curve must be a straight line.
the slope cannot be calculated without more information.
Answers
In the equation Y=13X+38 where Y is a function of X a) Y is a constant. b) 38 is a variable. c) the slope of the line is 13. d) None of these. 13) If Kolin catches 25 fish and gathers 70 fruits it would be co a) an efficient combination b) an unattainable combination c) an inefficient combination d) the most efficient combination Use the figure on the left to answer qucstions 14. 14. What is the equilibrium price and quantify? a. $35 and 6 dozens of roses per day b. $10 and 2 dozens of roses per day? c. Sis and 14 dozens of roses per day d. $25 and 10 dozens of roses per day
Answers
1)The slope of the line is C) 13. 2)It would be inefficient since it is not the most optimal use of resources.the correct option is C. 3)The equilibrium price and quantity are D) $25 and 10 dozens of roses per day, respectively.
1) Y = 13X + 38, where Y is a function of X.
The slope of the line is 13.
Therefore, the correct option is C.
2) Kolin catches 25 fish and gathers 70 fruits. If we consider the combination, then it would be inefficient since it is not the most optimal use of resources.
Therefore, the correct option is C.
3) Using the given figure, we can see that the point where the demand and supply curves intersect is the equilibrium point. At this point, the equilibrium price is $25 and the equilibrium quantity is 10 dozens of roses per day.
Therefore, the correct option is D. The equilibrium price and quantity are $25 and 10 dozens of roses per day, respectively.
Note that this is the point of intersection between the demand and supply curves, which represents the market equilibrium.
Know more about equilibrium price here,
https://brainly.com/question/29099220
#SPJ11
Models of inventory systems frequently consider the relationships among a beginning inventory,
a production quantity, a demand or sales, and an ending inventory. For a given
production period j, let
sj-1 = ending inventory from the previous period (beginning inventory for period j)
xj = production quantity in period j
dj = demand in period j
sj = ending inventory for period j
a. Write the mathematical relationship or model that shows ending inventory as a function
of beginning inventory, production, and demand.
b. What constraint should be added if production capacity for period j is given by Cj?
c. What constraint should be added if inventory requirements for period j mandate an
ending inventory of at least Ij?
Answers
a. This equation states that the ending inventory for period j (sj) is equal to the beginning inventory from the previous period (sj-1) plus the production quantity in period j (xj), minus the demand in period j (dj).
b. This constraint ensures that the production quantity in period j (xj) does not exceed the production capacity for that period (Cj).
c. This constraint ensures that the ending inventory for period j (sj) is greater than or equal to the required inventory level for that period (Ij).
a. The mathematical relationship or model that shows ending inventory as a function of beginning inventory, production, and demand can be represented as:
sj = sj-1 + xj - dj
This equation states that the ending inventory for period j (sj) is equal to the beginning inventory from the previous period (sj-1) plus the production quantity in period j (xj), minus the demand in period j (dj).
b. If the production capacity for period j is given by Cj, the constraint that should be added is:
xj ≤ Cj
This constraint ensures that the production quantity in period j (xj) does not exceed the production capacity for that period (Cj).
c. If inventory requirements for period j mandate an ending inventory of at least Ij, the constraint that should be added is:
sj ≥ Ij
This constraint ensures that the ending inventory for period j (sj) is greater than or equal to the required inventory level for that period (Ij).
Learn more about equation from
https://brainly.com/question/29174899
#SPJ11
Which trig function is used to solve for x if 53 is the reference angle?

Answers
The trigonometry used to solve for x in the right triangle is
A. tangent
What is tangent?In mathematics, the tangent is a trigonometric function that relates the ratio of the length of the opposite side to the length of the adjacent side in a right triangle. It is commonly abbreviated as tan.
The tangent function is defined for all real numbers except for certain values where the adjacent side is zero, resulting in division by zero. It takes an angle (measured in radians or degrees) as its input and returns the ratio of the length of the opposite side to the length of the adjacent side.
In a right triangle, if one of the acute angles is θ, then the tangent of θ (tan θ) is defined as:
tan θ = opposite side / adjacent side
tan 53 = x / 15
Learn more about tangent at
https://brainly.com/question/30162650
#SPJ1
PLZ HELP THIS IS DUE SOONNNN

Answers
Answer:
i cant see it... its like all torn up
Step-by-step explanation:
you know like a tv with no channel thats what its like for me
Energy and mass are related by the formula, e=mc2, where m is the mass of the object and c is the speed of light. the equation that finds m, given e and c, is
Answers
Energy and mass are related by the formula, E = mc², where m is the mass of the object and c is the speed of light. The equation that finds m, given e and c, is: m = E/c²
The equation, E = mc² was coined from Albert Einstein's theory of relativity, which shows the relationship between mass and energy. It shows that energy and mass can be interchanged into each other. The equation tells us that if we multiply the mass of a body (m) with the square of the speed of light (c²), we will get the total amount of energy (E) contained in that body, which can potentially be converted to other forms of energy.
However, if are given the energy contained in a body and the speed of light, then told to find the mass of the body, we will divide the equation by the coefficient of m. The coefficient of m in the equation is c², thus:
E = mc²
E/c² = mc²/c²
c² divided by c² is 1, therefore, the new equation is:
m = E/c²
Thus, the equation that finds m, given e and c is m = E/c².
Learn more about energy and mass here:
https://brainly.com/question/15219830
#SPJ4
a field goal is 3 points and the field goal after a touchdown is only 1 point. in a not-so-recent post-season, adam vinatieri of the indianapolis colts made a total of 21 field goals and extra point kicks for 49 points. find the number of field goals and extra points he made.
Answers
Adam Vinatieri made 14 field goals and 7 extra points.
Given that,
a field goal is 3 points and the field goal after a touchdown is only 1 point.
Adam Vinatieri made 21 field goals and extra point kicks for 49 points.
Let x be the number of field goals and y be the extra point kicks.
So we get,
x + y = 21 -------------(1)
3x + y = 49 -----------(2)
Subtracting equation (1) from equation (2),
2x = 28
x = 14
putting the value of x in equation (1),
14 + y = 21
y = 7
Therefore Adam Vinatieri made 14 field goals and 7 extra points.
Field goal means a score of three points in football made by drop kicking or placekicking the ball over the crossbar from ordinary play. A field goal is a successful kick of the ball by a kicker through the goalpost. It is an offensive play that can score three points for a team.
Adam Vinatieri is an American former football placekicker who played in the National Football League.
To know more about goal here
#https://brainly.com/question/15709602
#SPJ4