Solve inequality in interval notation Y^2>-5y-9
Answers
Related Questions
You are a sports agent’s assistant. You are preparing a report on contracts you have obtained for the agent’s clients. You recently negotiated the following annual contracts: $2.8 million, $18.9 million, $1.5 million, $1.2 million, $1.5 million, and $3.5 million per year. The standard deviation of the data is 6.3, and the range is 17.7.
Which measure of center is most appropriate, and what is the value of the measure of center?
A median; $1.35 million
B mode; $1.5 million
C median; $2.15 million
D mean; $4.9 million
E mean; $5.58 million
Answers
The data set is as follows, going from smallest to largest:
$1,2,000,000, $1.5,000,000, $1.5,000,000, $2.8,000,000, $3.5,000,000, and $18,9,000,000
The middle two figures are $2.8 million and $3.5 million because the data set has six items. These two values' average is:
($2.8 million plus $3.5 million) / 2= $1.35 million.
As a result, the median serves as the most accurate measure of the centre, and its value is $1.35 million. The median price is (A), or $1.35 million.
Describe Standard Deviation.Standard deviation is a statistical measure that indicates how much the values in a dataset deviate from the mean or average value of the dataset. It measures the spread or variability of the data around the mean.
The standard deviation is calculated by taking the square root of the variance of the dataset. The variance is the average of the squared differences between each data point and the mean. In other words, it measures how much the data points vary from the mean squared.
The formula for calculating the standard deviation is:
Standard deviation = sqrt( Sum \((x - mean)^2\) / (n - 1) )
where x is each data point in the dataset, mean is the average value of the dataset, and n is the number of data points in the dataset.
A higher standard deviation indicates that the values in the dataset are more spread out or have more variability, while a lower standard deviation indicates that the values are more tightly clustered around the mean.
Standard deviation is widely used in statistics and data analysis to measure the variability of data and to compare the spread of different datasets. It is used to assess the degree of risk and uncertainty associated with a given set of data, and it plays a crucial role in various fields, such as finance, engineering, and social sciences.
Given that we have a range and a standard deviation for the annual contracts obtained for the sports agent's clients, we can use these measures to determine the most appropriate measure of center.
The range is the difference between the largest and smallest values in the data set, which in this case is 17.7. The standard deviation is a measure of the spread of the data around the mean, which in this case is 6.3.
If the range is relatively small compared to the standard deviation, then the mean is the most appropriate measure of the center, since it takes into account the value of every data point. However, if the range is relatively large compared to the standard deviation, then the median is a more appropriate measure of center since it is less affected by extreme values in the data set.
In this case, the range of 17.7 is relatively large compared to the standard deviation of 6.3, which suggests that the median is the most appropriate measure of the center. We can find the median by arranging the data set in order from smallest to largest and finding the middle value. If there are an even number of values, we take the average of the two middle values.
The answer (B) mode; $1.5 million is incorrect because there are two modes ($1.5 million appears twice). The answers (D) mean; of $4.9 million and (E) mean; of $5.58 million are incorrect because the range is relatively large compared to the standard deviation, which indicates that the mean may be influenced by the extreme values in the data set.
To know more about the median visit:
brainly.com/question/3515636
#SPJ1
How many quarters of a meter are there in 4 3/4
Answers
Answer:
There are 19 quarters in 4 3/4
Hope that helps!
Answer:
I think it is 19 metres
Step-by-step explanation:
I think that is the answer
Helppp
The half-life of Radium-226 is 1590 years. If a sample contains 500 mg, how many mg will remain after 1000 years?---------
Answers
Using the exponential decay equation, we can see that after 1000 years we will have 178.43 mg of Ra₂₂₆
How much will remain after 1000 years?The decay of a radioactive substance, such as Radium-226, can be modeled by the exponential decay equation:
N(t) = N₀ * (1/2)^(t / T)
where:
N(t) is the amount of the substance remaining after time t
N₀ is the initial amount of the substance
t is the time elapsed
T is the half-life of the substance
Given that the half-life of Radium-226 is 1590 years and the initial amount is 500 mg, we can plug in these values into the equation and solve for N(1000), which represents the amount remaining after 1000 years.
N(1000) = 500 * (1/2)^(1000 / 1590)
N(1000) ≈ 178.43 mg
Learn more about half life at:
https://brainly.com/question/11152793
#SPJ1
12 and 35 Pythagorean theorem
Answers
Answer:
Hypotenuse = 37
Step-by-step explanation:
Let the base is 12 and height is 35.
We can use Pythagorean theorem to find the third side (hypotenuse or the longest side). The Pythagoras theorem can be given by :
\(H^2=b^2+h^2\\\\H^2=12^2+35^2\\\\H^2=1369\\\\H=\sqrt{1369} \\\\H=37\)
Hence, the hypotenuse is 37 units.
HELP PLEASE IT EASY!
+ no files please!!

Answers
Answer:
GIVEN :-
Ordered pairs given are :-
(2 , -1)(-5 , 3)(4 , 3)(-2 , -3.5)(0.5 , 1.75)TO FIND :-
Correct quadrant for each ordered pair.FACTS TO KNOW BEFORE SOLVING :-
While writing the co-ordinates of a point , its ordered pair is always in the form of ( x , y ) where x = x-coordinate of the point & y = y-coordinate of the point.In Quadrant 1 , the coordinates of a point is always = ( +x , +y ) because Quadrant 1 lies between the positive side of x-axis & positive side of y-axis.In Quadrant 2 , the coordinates of a point is always = ( -x , +y ) because Quadrant 2 lies between the negative side of x-axis & positive side of y-axis.In Quadrant 3 , the coordinates of a point is always = ( -x , -y ) because Quadrant 3 lies between the negative side of x-axis & negative side of y-axis.In Quadrant 4 , the coordinates of a points is always = ( +x , -y ) because Quadrant 4 lies between the positive side of x-axis & negative side of y-axis.SOLUTION :-
(2 , -1) is in Quadrant 4 because it's x-coordinate is positive whereas its y-coordinate is negative.(-5 , 3) is in Quadrant 2 because its x-coordinate is negative but y-coordinate is positive.(4 , 3) is in Quadrant 1 because both its x-coordinates & y-coordinates are positive.(-2 , -3.5) is in Quadrant 3 because both its x-coordinates & y-coordinates are negative.(0.5 , 1.75) is in Quadrant 1 because both its x-coordinates & y-coordinates are positive.Four friends share 3 sheets of construction paper equally.

Answers
Hope it help!!
Rewrite 2/11 and 1/7 so that they have a common denominator
Answers
Answer:its 22 and 7...........................
Step-by-step explanation:
Express 83 kilometers per hour in miles per hour.
...
mi/hr
(Round to the nearest hundredth as needed.)
Answers
Answer:
83 kilometres per hour =
51.574 miles per hour
can someone please help me with this question

Answers
Answer:
1.9.75x> 195
2.9.75x> 195
9.75/9.75x>195/9.75
x>20hrs
QUESTION 4 PATTERNS, FUNCTIONS AND ALGEBRA 1. Given 6x³-8x³+2+9x7-4x a. How many terms are there in the polynomial? State the degree of the polynomial c. Determine the value of the polynomial if x=-1 b.
Answers
Answers:
a) There are 5 termsb) Degree = 7c) The value is -1==========================================
Explanation:
a) Each term is separated by a plus or a minus.b) The degree is equal to the largest exponent. This applies to single variable polynomials only.c) Replace each x with -1. Then use the order of operations PEMDAS to simplify. You should get -1 as the answer. Use a calculator to confirm. It is a coincidence that we have the same input and output. This will not always happen with any general polynomial function.calculating area and circumference or perimeter of a 2d shape. use your measurements to calculate the area and circumference of the circle and to calculate the area and perimeter of the rectangle.
Answers
The area and perimeter of 2D shape of Rectangle is 6.8448cm and 11.04cm repectively. The area and perimeter of 2D shape of circle is 5.0761cm and 8.0028cm respectively.
2D shape of Rectangle with dimensions of Length is3.72 cm and Width is 1.84 cm. we can find the area of rectangle with formula Area = length x width and the formula of perimeter is Perimeter = 2(length + width).
Area = length x width = 3.72 cm x 1.84 cm = 6.8448 square cm (rounded to four decimal places)
Perimeter = 2(length + width) = 2(3.72 cm + 1.84 cm) = 11.04 cm
2D shape of Circle with dimension of diameter of 2.54 cm. we can find the area with formula Area = πr^2 and circumference with formula Circumference = 2πr
Radius = diameter / 2 = 2.54 cm / 2 = 1.27 cm
Area = πr^2 = π(1.27 cm)^2 = 5.0761 square cm (rounded to four decimal places)
Circumference = 2πr = 2π(1.27 cm) = 8.0028 cm (rounded to four decimal places)
To know more about 2D shapes.
https://brainly.com/question/18719120
#SPJ4
____The given question is incomplete, the complete question is given below:
Calculating area and circumference or perimeter of a 2D shape. Use your measurements to calculate the area and circumference of the circle and to calculate the area and perimeter of the rectangle. Rectangle Length: 3.72 cm Width: 1.84 cm Circle : 2.54 cm Diameter of circle
PLEASE HELP!!!
The population of Boomtown is currently 3000 and expected to grow by 4.7% over the next year. What will its population be by then?
The population of Dullsville, on the other hand, is currently 2000 and expected to decrease by 3.3% over the next year. What will its population be by then?
Answers
Answer: Population of Boomtown in next year = 3141
Population of Dullsville in next year = 2066
Step-by-step explanation:
i) Given: Current population of Boomtown is = 3000
growth rate = 4.7% = 0.047 [in decimal]
Growth in population in 1 year= (growth rate) x (Current population)
= 0.047 × 3000 =141
Population in next year = Current population + Growth in population in 1 year
= 3000 + 141 = 3141
Hence, population of Boomtown in next year = 3141
ii) Given: Current population of Dullsville is = 2000
growth rate = 3.3% = 0.033 [in decimal]
Growth in population in 1 year= (growth rate) x (Current population)
= 0.033 × 2000 =66
Population in next year = Current population + Growth in population in 1 year
= 2000 + 66= 2066
Hence, population of Dullsville in next year = 2066
Antonio weighs four pounds more than twice his brother weight. If Antonio weighs 97 pounds, how much does his brother weigh? Write and solve equation.
Answers
Answer:
The bother's weight is 46.5 lb.
Step-by-step explanation:
Let the brother's weight be b.
Antonio's weight is 2b + 4.
Antonio's weight is 97 lb.
2b + 4 = 97
2b = 93
b = 46.5 lb
Answer: The bother's weight is 46.5 lb.
What is the value of p for your parabola? I know the formula used to find P but I don't know what to divide by four in the formula to find P

Answers
Using the given graph of a parabola, let's find the value of P.
In a parabola, the value of P is the distance between the vertex and the focus.
From the graph, we have:
Focus : (6, 4)
Vertex: (6, 1)
Hence, to find the value of P, let's apply the distance formula.
\(\begin{gathered} p=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ p=\sqrt{(6-6)^2+(1-4)^2} \\ \\ p=\sqrt{0+(-3)^2} \\ \\ p=\sqrt{9} \\ \\ p=3 \end{gathered}\)Therefore, the value of p for the parabola is 3 .
• ANSWER:
p = 3
Find the missing side length.
Assume that all intersecting sides meet at right angles.
Be sure to include the correct unit in your answer.
13 ft
5 ft
?
9 ft
6 ft
4 ft

Answers
The measure of the missing side length from the given figure is 11 feet.
What is right angle?The right angle is created when two straight lines cross at a 90° angle or when they are perpendicular at the intersection.
It is referred to as a right angle if the angle formed by two rays exactly equals 90 degrees, or π/2.
The adjacent angles are right angles if a ray is positioned so that its terminus is on a line and they are equal.
In the given figure, assuming that all the intersecting sides meet at right angles.
So, the opposite sides are parallel to each other.
Let x be the length of missing side.
Thus, The length of missing side = Sum of length of parallel sides
Now, x= 5+6
= 11 feet
Therefore, the length of side missing is 11 feet.
To learn more about the right angle visit:
https://brainly.com/question/3770177.
#SPJ1

6428 rounded to the nearest hundred
Answers
Answer:
6400
Step-by-step explanation:
6428
4 is in the hundreds place
looking at the tens place = 2
Since it is less than 5
We leave the hundreds place alone
6400
What’s the correct answer for this?

Answers
Answer:
the third option
Step-by-step explanation:
the union of two sets of numbers just has to show all the numbers that are in the two sets, meaning if both sets have the same number, it is only shown once in the union
An inspector inspects large truckloads of potatoes to determine the proportion p in the shipment with major defects prior to using the potatoes to make potato chips. If there is clear evidence that this proportion is less than 0.10, she will accept the shipment. To reach a decision, she will test the hypotheses H0: p = 0.10 versus Ha: p < 0.10. To do so, she selects a simple random sample of 150 potatoes from the more than 3000 potatoes on the truck. Only 8 of the potatoes sampled are found to have major defects. What is the value of the large-sample z statistic?
An inspector inspects large truckloads of potatoes to determine the proportion p in the shipment with major defects prior to using the potatoes to make potato chips. If there is clear evidence that this proportion is less than 0.10, she will accept the shipment. To reach a decision, she will test the hypotheses H0: p = 0.10 versus Ha: p < 0.10. To do so, she selects a simple random sample of 150 potatoes from the more than 3000 potatoes on the truck. Only 8 of the potatoes sampled are found to have major defects. Compute the value of the large-sample z statistic. What is the P-value for this hypothesis test?
Answers
P-Value for the hypothesis test will be of z = 1.9065
The P-value for conducting the right-tailed test H0 : μ = 3 versus HA : μ > 3 is the probability that we would observe a test statistic greater than t* = 2.5 if the population mean
μ really were 3. Recall that probability equals the area under the probability curve. The P-value is therefore the area under a tn - 1 = t14 curve and to the right of the test statistic t* = 2.5. It can be shown using statistical software that the P-value is 0.0127
The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of HA if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0127, is less than
α
= 0.05, we reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ > 3.
Note that we would not reject H0 : μ = 3 in favor of HA : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P-value, 0.0254, is then greater than
α= 1.9065.
To learn more about hypothesis test.
https://brainly.com/question/14038154
#SPJ4
Explain how you used a mathematical model
to represent the situation. How did the model help you answer the
Main Question?
Answers
In mathematical modelling, we take a real-world problem and write it as an equivalent mathematical problem.
We then solve the mathematical problem, and interpret its solution in terms of the real-world problem.
After this we see to what extent the solution is valid in the context of the real-world problem.
Mathematical modeling is one of the bases of mathematics education. Mathematical modeling is described as conversion activity of a real problem in a mathematical form. Modeling involves to formulate the real-life situations or to convert the problems in mathematical explanations to a real or believable situation.
It's extremely precise, since it's math-based, which allows you to develop accurate ideas and assumptions. It's concise, with clear and established rules. It gives you direction when trying to solve a problem.
characters of modeling;
In mathematical models parameters are most often represented by variables. Changes in the numbers assigned to the variables change the model. 3) Simplification/Idealization.It should necessarily be incomplete.It may be changed or manipulated with relative ease.
It is simplification/Idealization. Mathematical modeling has many benefits related to real-world problems, but the main disadvantages are process simplification, specific rules of the model, and lack of information or data monitoring.
to know more about modeling ;
visit; brainly.com/question/20266588
#SPJ9
Item cost $430 sales tax was $8.60 what is the percentage of the sales tax rate
Answers
Answer:
2%
Step-by-step explanation:
You can write it out as equation first.
430*x%=8.60, leave x% alone, so the equation will change into
x%=8.60/430
8.60/430=0.02=2%
therefore, x%=2%
Amelia needs to buy some dog food. At the nearest store ,5 bags of dog food cost 12.50 how much would Amelia spend on three bags
Answers
Answer:
$7.50
Step-by-step explanation:
the question can be represented with:
12.5/5 and x/3
12.5/5 is 2.5, so that means each bag of dog food is $2.5
So then you multiply 2.5 by 3, = 1.20, so 3 bags of dog food is $7.50.
Answer:
Step-by-step explanation:
Remark
I take it you mean 5 and not 0.5.
If that is the case, this is a proportion question. A proportion consists of 4 parts. If you know 3 of the parts, you can solve for the 4th one.
Formula
Number of bags/Cost = new number of bags/Cost of the new number
Givens
original Number of bags = 5
Cost = 12.50
New number of bags = 3 bags
Cost = x
Solution
5/12.50 = 3/x Cross Multiply
5x = 12.50 * 3 Combine the right
5x = 37.5 Divide by 5
5x/5 = 37.5/5
x = 7.5
Answer: 3 bags cost 7.50 dollars.
A research firm conducted a study to determine the average amount of money that smokers spend on cigarettes during a week. The firm found that the population mean amount that all smokers spend on cigarettes is $20 and the population standard deviation is $5. What is the probability that a new sample this year of 100 steady smokers spends between $19 and $21 on average
Answers
Answer:
0.9544 = 95.44% probability that a new sample this year of 100 steady smokers spends between $19 and $21 on average
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
The firm found that the population mean amount that all smokers spend on cigarettes is $20 and the population standard deviation is $5.
This means that \(\mu = 20, \sigma = 5\)
Sample of 100:
This means that \(n = 100, s = \frac{5}{\sqrt{100}} = 0.5\)
What is the probability that a new sample this year of 100 steady smokers spends between $19 and $21 on average?
This is the pvalue of Z when X = 21 subtracted by the pvalue of Z when X = 19. So
X = 21
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{21 - 20}{0.5}\)
\(Z = 2\)
\(Z = 2\) has a pvalue of 0.9772
X = 19
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{19 - 20}{0.5}\)
\(Z = -2\)
\(Z = -2\) has a pvalue of 0.0228
0.9772 - 0.0228 = 0.9544
0.9544 = 95.44% probability that a new sample this year of 100 steady smokers spends between $19 and $21 on average
Find the Interpret the mean absolute deviation of the data 1/4,5/8,3/8,3/4,1/2
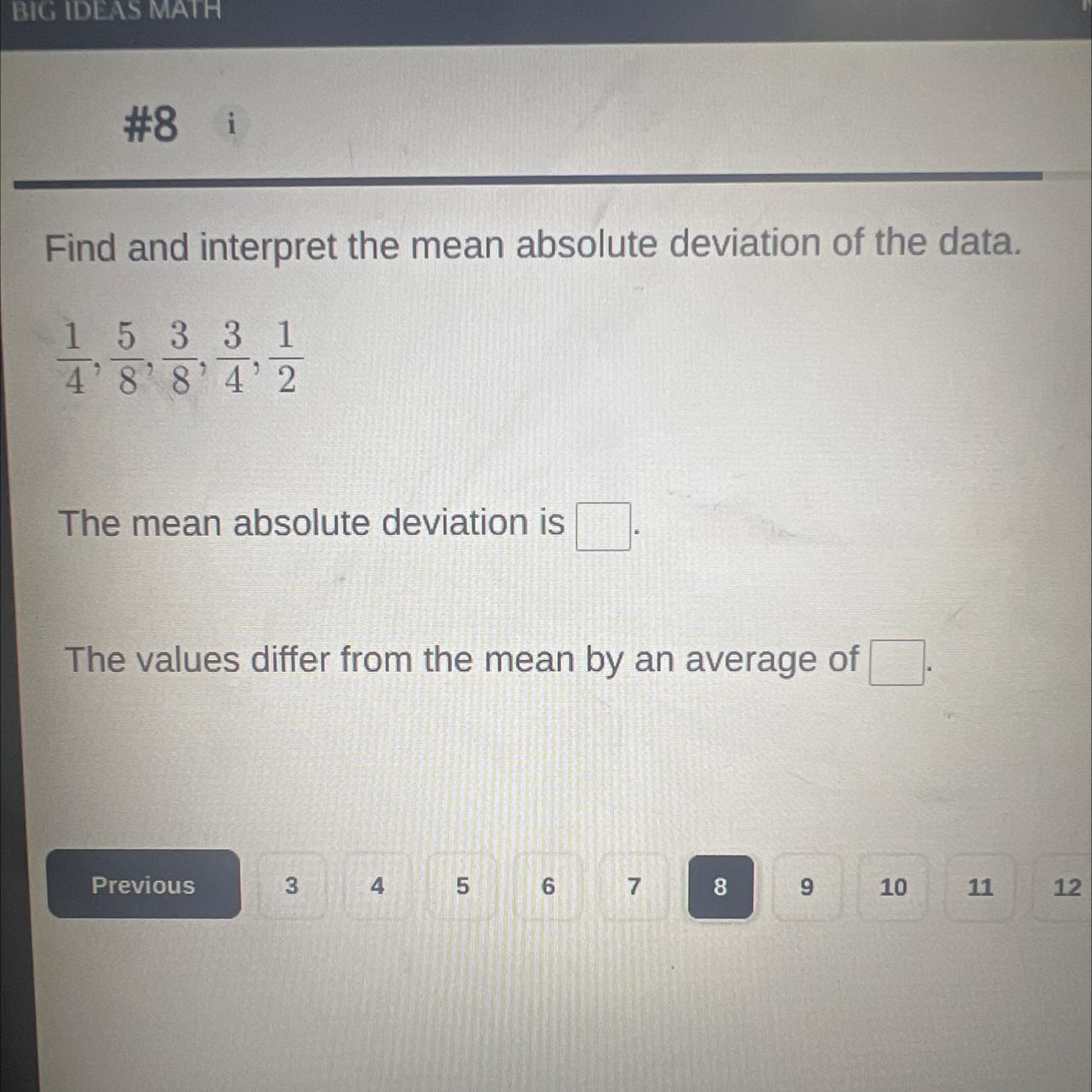
Answers
The mean absolute deviation (MAD) for the given data is 1/20. This means that, on average, each data point in the set differs from the mean by 1/20.
To find the mean absolute deviation (MAD) of a set of data, we need to calculate the average difference between each data point and the mean of the data set. Here's how we can calculate it for the given data:
Step 1: Find the mean (average) of the data set.
Mean = (1/4 + 5/8 + 3/8 + 3/4 + 1/2) / 5 = 2/5
Step 2: Calculate the difference between each data point and the mean.
Differences: |1/4 - 2/5|, |5/8 - 2/5|, |3/8 - 2/5|, |3/4 - 2/5|, |1/2 - 2/5|
Step 3: Calculate the absolute value of each difference.
Absolute Differences: 1/20, 1/40, 1/40, 1/20, 1/10
Step 4: Find the average of the absolute differences.
MAD = (1/20 + 1/40 + 1/40 + 1/20 + 1/10) / 5 = 1/20
The MAD provides a measure of the average amount of variation or dispersion in the data set. In this case, a MAD of 1/20 indicates that the data points are relatively close to the mean, with most values falling within 1/20 of the mean value.
For more such questions on mean absolute deviation
https://brainly.com/question/29545538
#SPJ8
Identify the next number in the following sequence
25 49 97 ?
Select only one answer
- 124
- 171
- 139
- 193
Answers
Answer:
the correct answer is 193
Step-by-step explanation:
25×1-0=25
25×2-1=49
49×2-1=97
97×2-1=193
4. For each babysitting job, Adam charges a fee for his bus fare plus an hourly rate. The graph shows how he calculates the cost of a babysitting job. Write a linear function in the form
y = mx + b to represent the situation.
Ay = 3x+2
B. y = 3x+1
C. y = 6x+2
D. y = -6× + 2
Answers
y = 6x + 2 is the function which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
The linear function in the form y = mx + b represents the situation where y represents the cost of the babysitting job
x represents the number of hours, "m" represents the hourly rate, and "b" represents the additional fee (bus fare).
y = 3x + 2 represents an hourly rate of 3 and an additional fee of 2.
y = 3x + 1 represents an hourly rate of 3 and an additional fee of 1.
y = 6x + 2 represents an hourly rate of 6 and an additional fee of 2.
y = -6x + 2 represents a negative hourly rate of -6 and an additional fee of 2.
Hence, y = 6x + 2 is the which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Please explain your answer to the question in the picture with steps

Answers
Answer:
x = 31.2
Step-by-step explanation:
You want the solution to the proportion 12/x = 5/13.
Rational equationYou can eliminate the fractions by multiplying this equation by the least common denominator. That value is 13x, the product of these denominators. Multiplying by 13x, we have ...
\(\dfrac{12}{x}\times13x=\dfrac{5}{13}\times13x\\\\\\12\cdot13=5\cdot x\qquad\text{simplified}\)
Now, the value of x is found by dividing both sides by its coefficient.
\(\dfrac{12\cdot13}{5}=\dfrac{5x}{5}\\\\\\\dfrac{156}{5}=x\\\\\boxed{31.2=x}\)
__
Additional comment
The first step we did, multiplying by 13x, is also sometimes called "cross multiplication." The result of that step is that each numerator is multiplied by the opposite denominator.
Multiplying both sides of the equation by the same value (13x) is supported by the multiplication property of equality. The term "cross multiplication" is descriptive of the result, but is not a recognized property of equality. It is a good idea to keep the math operations you do grounded in the properties of equality.
You will notice that the steps we did were "multiply by 13x" and "divide by 5". These can be done at once by "multiply by 13x/5". Of course, that operation is done to both sides of the equation.
Any proportion can be written 4 ways:
\(\dfrac{12}{x}=\dfrac{5}{13}\qquad\dfrac{x}{12}=\dfrac{13}{5}\qquad\dfrac{x}{13}=\dfrac{12}{5}\qquad\dfrac{13}{x}=\dfrac{5}{12}\)
These can be thought of as "upside down" and "sideways." We like the versions with the variable on top of a fraction, because the solution to that is simply multiplication by the variable's denominator.
<95141404393>
A square originally starts with an area of 64 cm. If each side of the square is increased by 2 cm, what is the area of the new square? A. 68 cm2 B. 72 cm2 C. 81 cm? D. 100 cm2
Answers
Answer:
D
Step-by-step explanation:
Hurry and anwser plz

Answers
Answer:
D
Step-by-step explanation:
103+103=206
360-206=154
154 divided by 2 equals 77 degrees aka D.
Hope this helped! :)
What is the volume of the shape below

Answers
The volume of the given figure is 1176 cubic cm.
The value of the figure is calculated by multiplying all three side areas. Volume is a measure of the amount of space that an object or a substance occupies. It is typically expressed in cubic units such as cubic meters (m³), cubic centimetres (cm³), or cubic feet (ft³).
The volume of the figure is calculated as,
Volume = 2 ( 15 x 6 + 20 x 6 + 20 x 18 )
Volume = 1176 Cubic cm
Hence, the volume of the figure will be equal to 1176 Cubic cm.
To know more about volume follow
https://brainly.com/question/29568631
#SPJ1
What is the midpoint of Line segment A B ?
Answers
Answer:
If the segment is horizontal or vertical, you can find the midpoint by dividing the length of the segment by 2 and counting that value from either of the endpoints. Example 1: Given the graph at the right, find the midpoint of and of . AB = 4 units (by counting). The midpoint is 2 units from either endpoints.